高中数学人教B版(2019)必修第二册节节通关练——5.3概率B(含解析)
文档属性
| 名称 | 高中数学人教B版(2019)必修第二册节节通关练——5.3概率B(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 347.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 09:53:00 | ||
图片预览




文档简介
一、单选题
1.《周易》集中华文明的精髓,是华夏智慧的结晶.该书认为天下万物皆由金、木、水、火、土五类元素组成,例如每个人的姓名,姓氏后面的名字中的字的五行属性都有具体的含义,如姓名“莫林波”,“林”属木,“波”属水.若一个人的姓氏后为两个字的名字,且每个字为哪种属性都是等可能的,则这两个字恰好五行属性不同的概率为
A. B. C. D.
2.有一副去掉了大小王的扑克牌,充分洗牌后,从中随机抽取一张,则抽到的牌为“黑桃”或“”的概率为( )
A. B. C. D.
3.已知消费者购买家用小电器有两种方式:网上购买和实体店购买.经工商局抽样调查发现,网上家用小电器合格率约为,而实体店里家用小电器的合格率约为,工商局12315电话接到关于家用小电器不合格的投诉,统计得知,被投诉的是在网上购买的概率约为.那么估计在网上购买家用小电器的人约占( )
A. B. C. D.
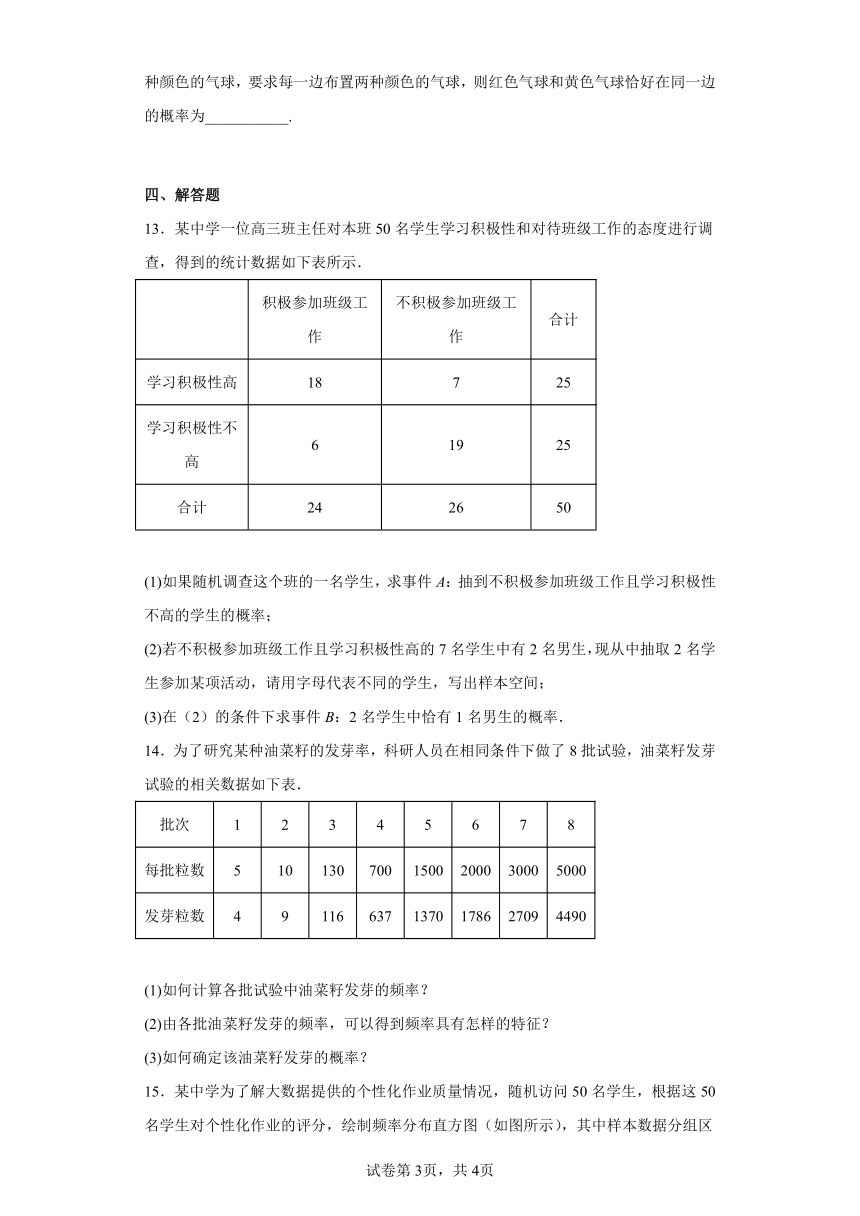
4.为保障食品安全,某监管部门对辖区内一家食品企业进行检查,现从其生产的某种产品中随机抽取100件作为样本,并以产品的一项关键质量指标值为检测依据,整理得到如下的样本频率分布直方图.若质量指标值在内的产品为一等品,则该企业生产的产品为一等品的概率约为( )
A.0.38 B.0.61
C.0.122 D.0.75
5.某班级从5名同学中挑出2名同学进行大扫除,若小王和小张在这5名同学之中,则小王和小张都没有被挑出的概率为( )
A. B. C. D.
6.掷一枚骰子的试验中,出现各点的概率均为,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+(表示事件B的对立事件)发生的概率为( )
A. B. C. D.
二、多选题
7.下列说法错误的有( )
A.随机事件A发生的概率是频率的稳定值,频率是概率的近似值
B.在同一次试验中,不同的基本事件不可能同时发生
C.任意事件A发生的概率满足
D.若事件A发生的概率趋近于0,则事件A是不可能事件
8.下列命题中是真命题的有( )
A.有A,B,C三种个体按的比例分层抽样调查,如果抽取的A个体数为9,则样本容量为30
B.一组数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲
D.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间内的频率为
三、填空题
9.银行储蓄卡的密码由6位数字组成,某人在银行自助取款机上取钱时,忘记了密码的最后1位数字,如果记得密码的最后1位是偶数,则第2次按对的概率是______.
10.在一次数学考试中,某班学生的及格率是,这里所说的“”是指___________.(填“频率”或“概率”)
11.甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响,则乙获胜的概率为___________.
12.某校为了庆祝六一儿童节,计划在学校花坛的左右两边布置红色 黄色 蓝色 绿色4种颜色的气球,要求每一边布置两种颜色的气球,则红色气球和黄色气球恰好在同一边的概率为___________.
四、解答题
13.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示.
积极参加班级工作 不积极参加班级工作 合计
学习积极性高 18 7 25
学习积极性不高 6 19 25
合计 24 26 50
(1)如果随机调查这个班的一名学生,求事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率;
(2)若不积极参加班级工作且学习积极性高的7名学生中有2名男生,现从中抽取2名学生参加某项活动,请用字母代表不同的学生,写出样本空间;
(3)在(2)的条件下求事件B:2名学生中恰有1名男生的概率.
14.为了研究某种油菜籽的发芽率,科研人员在相同条件下做了8批试验,油菜籽发芽试验的相关数据如下表.
批次 1 2 3 4 5 6 7 8
每批粒数 5 10 130 700 1500 2000 3000 5000
发芽粒数 4 9 116 637 1370 1786 2709 4490
(1)如何计算各批试验中油菜籽发芽的频率?
(2)由各批油菜籽发芽的频率,可以得到频率具有怎样的特征?
(3)如何确定该油菜籽发芽的概率?
15.某中学为了解大数据提供的个性化作业质量情况,随机访问50名学生,根据这50名学生对个性化作业的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间、、…、、.
(1)求频率分布直方图中的值;
(2)估计该中学学生对个性化作业评分不低于70的概率;
(3)从评分在的受访学生中,随机抽取2人,求此2人评分都在的概率.
16.从编号为A、B、C、D的4名男生和编号为m、n的2名女生中任选3人参加演讲比赛.
(1)把选中3人的所有可能情况一一列举出来;
(2)求所选3人中恰有一名女生的概率;
(3)求所选3人中至少有一名女生的概率
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.D
【解析】利用计数原理可得五行属性的所有可能情况,再利用古典概型的概率计算公式,即可得答案;
【详解】这两个字的五行属性的所有可能情况有种,
五行属性不同的情况有种,
故这两个字恰好五行属性不同的概率为.
故选:D.
【点睛】本题考查分步计数原理和古典概型的概率计算,考查逻辑推理能力、运算求解能力,属于基础题.
2.C
【分析】计算出抽到的牌为“黑桃”或“”所包含的牌的数量,利用古典概型的概率公式可求得结果.
【详解】由题意可知,该副扑克牌共张,其中“黑桃”共张,“”共张,
则抽到的牌为“黑桃”或“”共张,故所求概率为.
故选:C.
3.A
【分析】设在网上购买的人数占比为,实体店购买的人数占比为,分别求出各自被投诉的人数的占比,即可求解.
【详解】设在网上购买的人数占比为,实体店购买的人数占比为,
由题意可得,网上购买的合格率为,
则网上购买被投诉的人数占比为,实体店里购买的被投诉的人数占比为,
所以,解得.
故选:A.
【点睛】本题主要考查了概率的应用,其中解答中认真审题,求出各自被投诉的人数的占比是解答的关键,着重考查分析问题和解答问题的能力.
4.B
【分析】利用频率组距,即可得解.
【详解】根据频率分布直方图可知,质量指标值在内的概率
故选:B
5.B
【分析】记另3名同学分别为a,b,c,应用列举法求古典概型的概率即可.
【详解】记另3名同学分别为a,b,c,
所以基本事件为,,(a,小王),(a,小张),,(b,小王),(b,小张),(c,小王),(c,小张),(小王,小张),共10种.
小王和小张都没有被挑出包括的基本事件为,,,共3种,
综上,小王和小张都没有挑出的概率为.
故选:B.
6.C
【分析】由题意知试验发生包含的所有事件共有6种,事件和事件是互斥事件,看出事件和事件包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
【详解】解:事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:C.
7.CD
【分析】根据概率与频率的关系判断①正确,根据基本事件的特点判断②正确,根据必然事件,不可能事件,随机事件的概念判断③错误,根据小概率事件的概念判断④错误.
【详解】∵随机事件A发生的概率是频率的稳定值,频率是概率的近似值,∴A中说法正确;
基本事件的特点是任意两个基本事件是互斥的,∴在同一次试验中,不同的基本事件不可能同时发生,∴B中说法正确;
必然事件发生的概率为1,不可能事件发生的概率为0,随机事件发生的概率大于0且小于1.∴任意事件A发生的概率P(A)满足.∴C中说法错误;
若事件A发生的概率趋近于0,则事件A是小概率事件,但不是不可能事件,∴D中说法错误.
故选CD
【点睛】本题主要考查了概率的概念和有关性质,属于概念辨析题,对一些易混概念必须区分清.
8.BD
【分析】利用分层抽样中样本的抽样比等于各层的抽样比即可判断A,求出这一组数据的平均数、众数、中位数即可判B,计算乙的方差,比较方差大小即可判断C,利用落在区间内的个数除以总的个数计算概率,即可判断D,从而得出正确选项.
【详解】对于选项A:根据样本的抽样比等于各层的抽样比,样本容量为,故选项A 不正确;
对于选项B:数据1,2,3,3,4,5的平均数为,众数和中位数都是,故选项B正确;
对于选项C:乙组数据的平均数为,乙组数据的方差为
,所以这两组数据中较稳定的是乙,故选项C不正确;
对于选项D:样本数据落在区间有120,122,116,120有个,所以样本数据落在区间内的频率为,故选项D正确,
故选:BD
9.##0.2
【分析】利用古典概型的概率公式求概率.
【详解】连续按两个不同的偶数共有种不同的按法,其中第二次才按对的按法有4种,所以事件记得密码的最后1位是偶数,则第2次按对的概率,
故答案为:.
10.频率
【分析】根据频率与概率的概念即可得出答案.
【详解】解析:在一次数学考试中,某班学生的及格率是,
这里所说的“”是指“频率”.
只有经过很多次考试得到的及格率都是,才能说是概率.
故答案为:频率.
11.
【分析】根据规则先投中者获胜,则乙要先投进才获胜,分情况讨论,求各个情况下概率和即可.
【详解】记“乙获胜”为事件C,记甲第次投篮投进为事件,乙第次投篮投进为事件,
由互斥事件仅有一个发生的概率与相互独立事件同时发生的概率计算公式知,
.
故答案:
12.
【分析】列举出所有结果,然后由古典概型的概率公式可得.
【详解】在学校花坛的左右两边布置气球的所有可能结果有(红黄,蓝绿),(红蓝,黄绿),(红绿,黄蓝),(黄蓝,红绿),(黄绿,红蓝),(蓝绿,红黄),共6种,其中红色气球和黄色气球恰好在同一边的所有可能结果有(红黄,蓝绿),(蓝绿,红黄),共2种,所以红色气球和黄色气球恰好在同一边的概率为.
故答案为:
13.(1)
(2)答案见解析
(3)
【分析】(1)名学生中,不积极参加班级工作且学习积极性不高的学生有19人,由此能求出事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率.
(2)不积极参加班级工作且学习积极性高的7名学生中有两名男生,设为A,B,另外五名女生设为a,b,c,d,e,现从中抽取两名学生参加某项活动,能用字母代表不同的学生列举出抽取的所有可能结果.
(3)事件B:两名学生中恰有1名男生,则事件B包含的基本事件有10种,由此能求出事件B:两名学生中恰有1名男生的概率.
(1)
名学生中,不积极参加班级工作且学习积极性不高的学生有19人,
事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率.
(2)
不积极参加班级工作且学习积极性高的7名学生中有两名男生,设为A,B,另外五名女生设为a,b,c,d,e,
现从中抽取两名学生参加某项活动,
用字母代表不同的学生列举出抽取的所有可能结果有21种,分别为:
AB,Aa,Ab,Ac,Ad,Ae,Ba,Bb,Bc,Bd,Be,ab,ac,ad,ae,bc,bd,be,cd,ce,de.
(3)
事件B:两名学生中恰有1名男生,
则事件B包含的基本事件有10种,分别为:
Aa,Ab,Ac,Ad,Ae,Ba,Bb,Bc,Bd,Be,
事件B:两名学生中恰有1名男生的概率.
14.(1)答案见解析
(2)答案见解析
(3)0.900
【分析】(1)根据频率的定义说明;
(2)计算频率,归纳出规律;
(3)根据概率的意义确定.
(1)
利用公式:频率,可求出各批试验中油菜籽发芽的频率.
(2)
,,,,,,,,
当试验次数越来越多时,频率越来越趋近于一个常数.
(3)
由(2)可知,当试验次数越来越多时,频率在0.900附近波动,由此可估计该油菜籽发芽的概率约为0.900.
15.(1);(2);(3).
【分析】(1)可根据频率分布直方图得出结果;
(2)可通过后三组的频率之和得出结果;
(3)本题首先可令5名受访职工依次为、、、、,然后列出随机抽取2人的所有可能情况以及抽取2人的评分都在的所有可能情况,最后根据古典概型的概率计算公式即可得出结果.
【详解】(1),解得.
(2)由频率分布直方图易知:
50名受访学生评分不低于70的频率为,
故该中学学生对个性化作业评分不低于70的概率的估计值为.
(3)受访学生评分在的有人,依次为、、,
受访学生评分在的有人,依次为、,
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,依次为:
、、、、、、、、、,
因为所抽取2人的评分都在的结果有3种,依次为、、,
所以此2人评分都在的概率.
16.(1)答案见解析
(2)
(3)
【分析】(1)列举法写出基本事件;
(2)结合古典概型概率公式即可求出结果;
(3)结合古典概型概率公式即可求出结果.
(1)
设4名男生分别为A,B,C,D,两名女生分别为m,n,则从6名学生中任3人的所有情况有:,,,,,,,,,,,,,,,,,,,,共20种,
(2)
由(1)可知共有20种情况,其中所选3人中恰有一名女生的有12种,
所以所求概率为,
(3)
由(1)可知共有20种情况,所选3人中至少有一名女生的有16种,
所以所求概率为
答案第1页,共2页
答案第1页,共2页
1.《周易》集中华文明的精髓,是华夏智慧的结晶.该书认为天下万物皆由金、木、水、火、土五类元素组成,例如每个人的姓名,姓氏后面的名字中的字的五行属性都有具体的含义,如姓名“莫林波”,“林”属木,“波”属水.若一个人的姓氏后为两个字的名字,且每个字为哪种属性都是等可能的,则这两个字恰好五行属性不同的概率为
A. B. C. D.
2.有一副去掉了大小王的扑克牌,充分洗牌后,从中随机抽取一张,则抽到的牌为“黑桃”或“”的概率为( )
A. B. C. D.
3.已知消费者购买家用小电器有两种方式:网上购买和实体店购买.经工商局抽样调查发现,网上家用小电器合格率约为,而实体店里家用小电器的合格率约为,工商局12315电话接到关于家用小电器不合格的投诉,统计得知,被投诉的是在网上购买的概率约为.那么估计在网上购买家用小电器的人约占( )
A. B. C. D.
4.为保障食品安全,某监管部门对辖区内一家食品企业进行检查,现从其生产的某种产品中随机抽取100件作为样本,并以产品的一项关键质量指标值为检测依据,整理得到如下的样本频率分布直方图.若质量指标值在内的产品为一等品,则该企业生产的产品为一等品的概率约为( )
A.0.38 B.0.61
C.0.122 D.0.75
5.某班级从5名同学中挑出2名同学进行大扫除,若小王和小张在这5名同学之中,则小王和小张都没有被挑出的概率为( )
A. B. C. D.
6.掷一枚骰子的试验中,出现各点的概率均为,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+(表示事件B的对立事件)发生的概率为( )
A. B. C. D.
二、多选题
7.下列说法错误的有( )
A.随机事件A发生的概率是频率的稳定值,频率是概率的近似值
B.在同一次试验中,不同的基本事件不可能同时发生
C.任意事件A发生的概率满足
D.若事件A发生的概率趋近于0,则事件A是不可能事件
8.下列命题中是真命题的有( )
A.有A,B,C三种个体按的比例分层抽样调查,如果抽取的A个体数为9,则样本容量为30
B.一组数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲
D.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间内的频率为
三、填空题
9.银行储蓄卡的密码由6位数字组成,某人在银行自助取款机上取钱时,忘记了密码的最后1位数字,如果记得密码的最后1位是偶数,则第2次按对的概率是______.
10.在一次数学考试中,某班学生的及格率是,这里所说的“”是指___________.(填“频率”或“概率”)
11.甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响,则乙获胜的概率为___________.
12.某校为了庆祝六一儿童节,计划在学校花坛的左右两边布置红色 黄色 蓝色 绿色4种颜色的气球,要求每一边布置两种颜色的气球,则红色气球和黄色气球恰好在同一边的概率为___________.
四、解答题
13.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示.
积极参加班级工作 不积极参加班级工作 合计
学习积极性高 18 7 25
学习积极性不高 6 19 25
合计 24 26 50
(1)如果随机调查这个班的一名学生,求事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率;
(2)若不积极参加班级工作且学习积极性高的7名学生中有2名男生,现从中抽取2名学生参加某项活动,请用字母代表不同的学生,写出样本空间;
(3)在(2)的条件下求事件B:2名学生中恰有1名男生的概率.
14.为了研究某种油菜籽的发芽率,科研人员在相同条件下做了8批试验,油菜籽发芽试验的相关数据如下表.
批次 1 2 3 4 5 6 7 8
每批粒数 5 10 130 700 1500 2000 3000 5000
发芽粒数 4 9 116 637 1370 1786 2709 4490
(1)如何计算各批试验中油菜籽发芽的频率?
(2)由各批油菜籽发芽的频率,可以得到频率具有怎样的特征?
(3)如何确定该油菜籽发芽的概率?
15.某中学为了解大数据提供的个性化作业质量情况,随机访问50名学生,根据这50名学生对个性化作业的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间、、…、、.
(1)求频率分布直方图中的值;
(2)估计该中学学生对个性化作业评分不低于70的概率;
(3)从评分在的受访学生中,随机抽取2人,求此2人评分都在的概率.
16.从编号为A、B、C、D的4名男生和编号为m、n的2名女生中任选3人参加演讲比赛.
(1)把选中3人的所有可能情况一一列举出来;
(2)求所选3人中恰有一名女生的概率;
(3)求所选3人中至少有一名女生的概率
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.D
【解析】利用计数原理可得五行属性的所有可能情况,再利用古典概型的概率计算公式,即可得答案;
【详解】这两个字的五行属性的所有可能情况有种,
五行属性不同的情况有种,
故这两个字恰好五行属性不同的概率为.
故选:D.
【点睛】本题考查分步计数原理和古典概型的概率计算,考查逻辑推理能力、运算求解能力,属于基础题.
2.C
【分析】计算出抽到的牌为“黑桃”或“”所包含的牌的数量,利用古典概型的概率公式可求得结果.
【详解】由题意可知,该副扑克牌共张,其中“黑桃”共张,“”共张,
则抽到的牌为“黑桃”或“”共张,故所求概率为.
故选:C.
3.A
【分析】设在网上购买的人数占比为,实体店购买的人数占比为,分别求出各自被投诉的人数的占比,即可求解.
【详解】设在网上购买的人数占比为,实体店购买的人数占比为,
由题意可得,网上购买的合格率为,
则网上购买被投诉的人数占比为,实体店里购买的被投诉的人数占比为,
所以,解得.
故选:A.
【点睛】本题主要考查了概率的应用,其中解答中认真审题,求出各自被投诉的人数的占比是解答的关键,着重考查分析问题和解答问题的能力.
4.B
【分析】利用频率组距,即可得解.
【详解】根据频率分布直方图可知,质量指标值在内的概率
故选:B
5.B
【分析】记另3名同学分别为a,b,c,应用列举法求古典概型的概率即可.
【详解】记另3名同学分别为a,b,c,
所以基本事件为,,(a,小王),(a,小张),,(b,小王),(b,小张),(c,小王),(c,小张),(小王,小张),共10种.
小王和小张都没有被挑出包括的基本事件为,,,共3种,
综上,小王和小张都没有挑出的概率为.
故选:B.
6.C
【分析】由题意知试验发生包含的所有事件共有6种,事件和事件是互斥事件,看出事件和事件包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
【详解】解:事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:C.
7.CD
【分析】根据概率与频率的关系判断①正确,根据基本事件的特点判断②正确,根据必然事件,不可能事件,随机事件的概念判断③错误,根据小概率事件的概念判断④错误.
【详解】∵随机事件A发生的概率是频率的稳定值,频率是概率的近似值,∴A中说法正确;
基本事件的特点是任意两个基本事件是互斥的,∴在同一次试验中,不同的基本事件不可能同时发生,∴B中说法正确;
必然事件发生的概率为1,不可能事件发生的概率为0,随机事件发生的概率大于0且小于1.∴任意事件A发生的概率P(A)满足.∴C中说法错误;
若事件A发生的概率趋近于0,则事件A是小概率事件,但不是不可能事件,∴D中说法错误.
故选CD
【点睛】本题主要考查了概率的概念和有关性质,属于概念辨析题,对一些易混概念必须区分清.
8.BD
【分析】利用分层抽样中样本的抽样比等于各层的抽样比即可判断A,求出这一组数据的平均数、众数、中位数即可判B,计算乙的方差,比较方差大小即可判断C,利用落在区间内的个数除以总的个数计算概率,即可判断D,从而得出正确选项.
【详解】对于选项A:根据样本的抽样比等于各层的抽样比,样本容量为,故选项A 不正确;
对于选项B:数据1,2,3,3,4,5的平均数为,众数和中位数都是,故选项B正确;
对于选项C:乙组数据的平均数为,乙组数据的方差为
,所以这两组数据中较稳定的是乙,故选项C不正确;
对于选项D:样本数据落在区间有120,122,116,120有个,所以样本数据落在区间内的频率为,故选项D正确,
故选:BD
9.##0.2
【分析】利用古典概型的概率公式求概率.
【详解】连续按两个不同的偶数共有种不同的按法,其中第二次才按对的按法有4种,所以事件记得密码的最后1位是偶数,则第2次按对的概率,
故答案为:.
10.频率
【分析】根据频率与概率的概念即可得出答案.
【详解】解析:在一次数学考试中,某班学生的及格率是,
这里所说的“”是指“频率”.
只有经过很多次考试得到的及格率都是,才能说是概率.
故答案为:频率.
11.
【分析】根据规则先投中者获胜,则乙要先投进才获胜,分情况讨论,求各个情况下概率和即可.
【详解】记“乙获胜”为事件C,记甲第次投篮投进为事件,乙第次投篮投进为事件,
由互斥事件仅有一个发生的概率与相互独立事件同时发生的概率计算公式知,
.
故答案:
12.
【分析】列举出所有结果,然后由古典概型的概率公式可得.
【详解】在学校花坛的左右两边布置气球的所有可能结果有(红黄,蓝绿),(红蓝,黄绿),(红绿,黄蓝),(黄蓝,红绿),(黄绿,红蓝),(蓝绿,红黄),共6种,其中红色气球和黄色气球恰好在同一边的所有可能结果有(红黄,蓝绿),(蓝绿,红黄),共2种,所以红色气球和黄色气球恰好在同一边的概率为.
故答案为:
13.(1)
(2)答案见解析
(3)
【分析】(1)名学生中,不积极参加班级工作且学习积极性不高的学生有19人,由此能求出事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率.
(2)不积极参加班级工作且学习积极性高的7名学生中有两名男生,设为A,B,另外五名女生设为a,b,c,d,e,现从中抽取两名学生参加某项活动,能用字母代表不同的学生列举出抽取的所有可能结果.
(3)事件B:两名学生中恰有1名男生,则事件B包含的基本事件有10种,由此能求出事件B:两名学生中恰有1名男生的概率.
(1)
名学生中,不积极参加班级工作且学习积极性不高的学生有19人,
事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率.
(2)
不积极参加班级工作且学习积极性高的7名学生中有两名男生,设为A,B,另外五名女生设为a,b,c,d,e,
现从中抽取两名学生参加某项活动,
用字母代表不同的学生列举出抽取的所有可能结果有21种,分别为:
AB,Aa,Ab,Ac,Ad,Ae,Ba,Bb,Bc,Bd,Be,ab,ac,ad,ae,bc,bd,be,cd,ce,de.
(3)
事件B:两名学生中恰有1名男生,
则事件B包含的基本事件有10种,分别为:
Aa,Ab,Ac,Ad,Ae,Ba,Bb,Bc,Bd,Be,
事件B:两名学生中恰有1名男生的概率.
14.(1)答案见解析
(2)答案见解析
(3)0.900
【分析】(1)根据频率的定义说明;
(2)计算频率,归纳出规律;
(3)根据概率的意义确定.
(1)
利用公式:频率,可求出各批试验中油菜籽发芽的频率.
(2)
,,,,,,,,
当试验次数越来越多时,频率越来越趋近于一个常数.
(3)
由(2)可知,当试验次数越来越多时,频率在0.900附近波动,由此可估计该油菜籽发芽的概率约为0.900.
15.(1);(2);(3).
【分析】(1)可根据频率分布直方图得出结果;
(2)可通过后三组的频率之和得出结果;
(3)本题首先可令5名受访职工依次为、、、、,然后列出随机抽取2人的所有可能情况以及抽取2人的评分都在的所有可能情况,最后根据古典概型的概率计算公式即可得出结果.
【详解】(1),解得.
(2)由频率分布直方图易知:
50名受访学生评分不低于70的频率为,
故该中学学生对个性化作业评分不低于70的概率的估计值为.
(3)受访学生评分在的有人,依次为、、,
受访学生评分在的有人,依次为、,
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,依次为:
、、、、、、、、、,
因为所抽取2人的评分都在的结果有3种,依次为、、,
所以此2人评分都在的概率.
16.(1)答案见解析
(2)
(3)
【分析】(1)列举法写出基本事件;
(2)结合古典概型概率公式即可求出结果;
(3)结合古典概型概率公式即可求出结果.
(1)
设4名男生分别为A,B,C,D,两名女生分别为m,n,则从6名学生中任3人的所有情况有:,,,,,,,,,,,,,,,,,,,,共20种,
(2)
由(1)可知共有20种情况,其中所选3人中恰有一名女生的有12种,
所以所求概率为,
(3)
由(1)可知共有20种情况,所选3人中至少有一名女生的有16种,
所以所求概率为
答案第1页,共2页
答案第1页,共2页
