高中数学人教B版(2019)必修第二册节节通关练——5.1统计C(含解析)
文档属性
| 名称 | 高中数学人教B版(2019)必修第二册节节通关练——5.1统计C(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 547.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 09:54:59 | ||
图片预览




文档简介
一、单选题
1.某大学为了解该校学生的体重情况,从中抽取了若干个样本进行研究,将数据整理后得到如图所示的频率分布直方图,已知图中从左到右前四组的频率之比为,其中第二组的频数为60,则下列说法错误的是( )
A.抽取的样本量为400
B.样本中体重在的频率为0.25
C.若该大学共有学生36000人,则体重超过的估计有600人
D.估计抽取的学生体重的中位数约为66
2.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
4.高三模拟考试常常划定的总分各批次分数线,通过一定的数学模型,确定不同学科在一本、二本等各批次“学科上线有双分”的分数线.考生总成绩达到总分各批次分数线的称为总分上线;考生某一单科成绩达到及学科上线有双分的称为单科上线.学科对总分的贡献或匹配程度评价有很大的意义.利用“学科对总分上线贡献率”和“学科有效分上线命中率”这两项评价指标,来反映各学科的单科成绩对考生总分上线的贡献与匹配程度,这对有效安排备考复习计划具有十分重要的意义.某州一诊考试划定总分一本线为465分,数学一本线为104分,某班一小组的总分和数学成绩如表,则该小组“数学学科对总分上线贡献率、有效分上线命中率”分别是( )(结果保留到小数点后一位有效数字)
学生编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
数学成绩 120 117 122 101 100 112 99 111 102 100 89 98 92 84 94 113 97 104 85 85
总分成绩 495 494 493 485 483 483 482 480 479 475 471 470 463 457 454 453 448 448 441 440
A.41.7%,71.4% B.60%,71.4%
C.41.7%,35% D.60%,35%
5.从分别写有的张卡片中随机抽取张,放回后再随机抽取张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
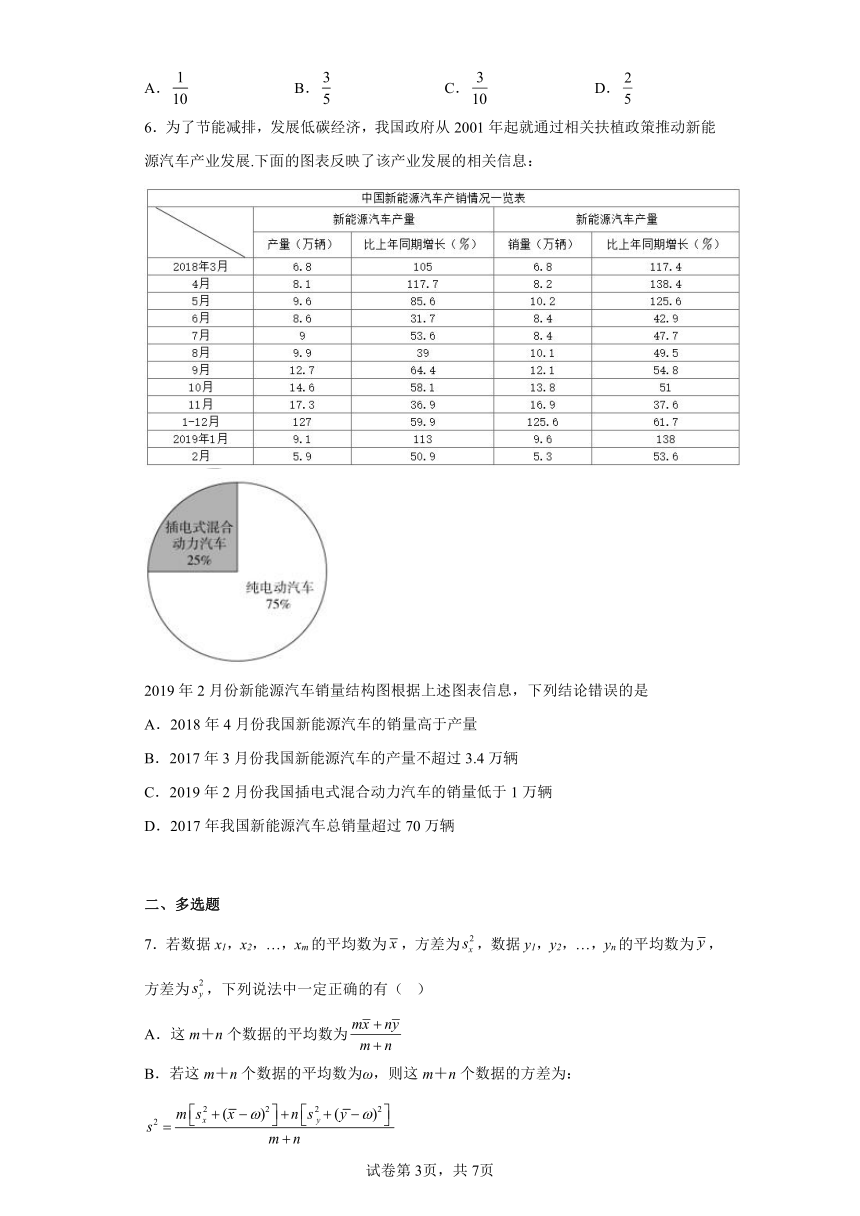
6.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
二、多选题
7.若数据x1,x2,…,xm的平均数为,方差为,数据y1,y2,…,yn的平均数为,方差为,下列说法中一定正确的有( )
A.这m+n个数据的平均数为
B.若这m+n个数据的平均数为ω,则这m+n个数据的方差为:
C.若m=n,,则
D.若m=n,,则
8.已知在一次射击预选赛中,甲 乙两人各射击次,两人成绩(所中环数越大,成绩越好)的频数分布表分别为:
环数
甲中频数
环数
乙中频数
下面判断正确的是( )A.甲所中环数的平均数大于乙所中环数的平均数
B.甲所中环数的中位数小于乙所中环数的中位数
C.甲所中环数的方差小于乙所中环数的方差
D.甲所中环数的方差大于乙所中环数的方差
三、填空题
9.已知样本数据,,,的均值,则样本数据,,,的均值为_______.
10.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产.设该工厂连续5天生产的口罩数依次为,,,,(单位:十万只),若这组数据,,,,的方差为1.44,且,,,,的平均数为4,则该工厂这5天平均每天生产口罩__________十万只.
11.佩香囊是端午节传统习俗之一,香囊内通常填充一些中草药,有清香、驱虫的功效.经研究发现一批香囊中一种草药甲的含量x(单位:克)与香囊功效y之间满足,现从中随机抽取了6个香囊,得到香囊中草药甲的含量的平均数为6克,香囊功效的平均数为15,则这6个香囊中草药甲含量的标准差为______克.
12.某企业三月中旬生产A、B、C三种产品共3000件,根据分层抽样的结果,企业统计员作了如下统计表格.
产品类别 A B C
产品数量(件) 1300
样本容量(件) 130
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是___________.
四、解答题
13.2020年1月8日,在“不忘初心 牢记使命”主题教育总结大会上,习总书记指出:“要把学习贯彻党的创新理论作为思想武装的重中之重,同学习党史 新中国史 改革开放史 社会主义发展史结合起来.”为了提高思想认识,某校开展了“学史明鉴 牢记使命”知识竞赛活动,从950名参赛的学生中随机选取100人的成绩作为样本,得到如图所示的频率分布直方图.
(1)现将全体参赛学生成绩编号为001--950,使用附图提供的“随机数表”从第二行的第三个数开始从左往右抽,请写出前3个被抽到样本编号;
(2)求频率分布直方图中的值,并估计该校此次参赛学生成绩的平均分(同一组数据用该组区间的中点值代表).
附图:
14.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),表示购机的同时购买的易损零件数.
(Ⅰ)若=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
15.2021年新冠疫情仍未平息,接种疫苗是防止新冠疫情最有效的手段今年5月,某地区疫苗接种出现了排长队现象,为了了解该地区接种人群的等待时间(从到达接种点到接种完成,不包括接种后的观察时间),随机调查了该地区某天接种的100人,制成了如下频率分布直方图.
(1)求样本中等待时间大于60分钟的人数;
(2)根据频率分布直方图,估计这100名接种者等待时间的平均值(各组区间的数据以该组区间的中间值作代表).
16.2021年3月18日,位于孝感市孝南区长兴工业园内的湖北福益康医疗科技有限公司正式落地投产,这是孝感市第一家获批的具有省级医疗器械生产许可证资质的企业,也是我市首家“一次性使用医用口罩、医用外科口罩”生产企业。在暑期新冠肺炎疫情反弹期间,该公司加班加点生产口罩、防护服,消毒水等防疫物品,保障抗疫一线医疗物资供应,在社会上赢得一片赞誉.在加大生产的同时,该公司狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:,,,…,,得到如下频率分布直方图.
(1)求出直方图中m的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表,中位数精确到);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,其中一等品和二等品分别有多少个.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据后四组的频率值可得前四组的频率之和,从而可求出第二组的频率,从而可求出抽取的样本量,故可判断选项A;
根据前四组的频率之和及前四组的频率之比为,可计算出体重在的频率,故可判断选项B;
通过样本中体重超过的频率可估计大学共有学生36000人时,体重超过的人数,从而可判断选项C;
利用频率分布直方图估计中位数的方法可计算出中位数,故可判断选项D.
【详解】由后四组的频率值可得前四组的频率之和为,
所以第二组的频率为,所以抽取的样本量为,故A正确;
体重在的频率为,B正确;
若该大学共有学生36000人,则体重超过的估计有人,C错误;
设抽取学生体重的中位数为,则,解得,D正确.
故选:C.
2.A
【分析】可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
【点睛】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
3.A
【分析】首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
4.A
【分析】由题知,双过线人数为5人,单过线人数为7人,总分过线人数为12人,进而根据题意求解即可;
【详解】解:由图表知双过线人数为5人,单过线人数为7人,总分过线人数为12人;
“学科对总分上线贡献率”为,
“学科有效分上线命中率”为,
故选:A.
【点睛】本题考查统计的应用,考查数据分析与处理能力,是中档题.本题解题的关键在于根据已知,读懂试题,在理解的基础上,进行数据分析处理计算.
5.D
【详解】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
基本事件总数n=5×5=25,
抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),
共有m=10个基本事件,
∴抽得的第一张卡片上的数大于第二张卡片上的数的概率p=
故答案为D.
6.C
【解析】根据图表中的数据的分析处理及进行简单的合情推理,逐一检验,即可求解.
【详解】由图表可知:
对于选项A中,2018年4月份我国新能源汽车的销量为8.2万辆,产量为8.1万辆,所以是正确的;
对于选项B中,2017年3月份我国新能源汽车的产量为万辆,所以是正确的;
对于选项C中,2019年2月份我国插电混合动力汽车的销量为万辆,所以不正确;
对于D中,2017年我国新能源汽车总销量为万辆,所以是正确的,
故选C.
【点睛】本题主要考查了对图表数据的分析处理,以及简单的合情推理的应用,其中解答中认真审题,根据图表的信息逐项判定是解答的关键,着重考查了推理与运算能力,属于基础题.
7.ABC
【分析】直接利用均值和方差的关系,方差和均值的性质,应用判断A,B,C,D的结论.
【详解】解:对于A,若数据x1,x2,…,xm的平均数为,数据y1,y2,…,yn的平均数为,
则m+n个数据的平均数为,故选项A正确;
对于B,由于m+n个数据的平均数为,若数据x1,x2,…,xm的方差为,数据y1,y2,…,yn的方差为,由方差的计算式得,这m+n个数据的方差为:,
又,所以,则, 所以
同理可得:,,
,故选项B正确;
对于C,若m=n,,则,故选项C正确;
对于D,若m=n,,则.
故选项D错误.
故选:ABC.
8.AC
【分析】根据随机变量的特征数据验证各选项得出答案.
【详解】解析:甲所中环数的平均数为
乙所中环数的平均数为:
所以甲所中环数的平均数大于乙所中环数的平均数,选项正确;
甲所中环数的中位数为:,乙所中环数的中位数为:
所以甲所中环数的中位数大于乙所中环数的中位数,选项B错误;甲所中环数的方差为:,乙所中环数的方差为:
所以乙所中环数的方差大于甲所中环数的方差,选项正确;选项错误.
故选:AC.
9.
【详解】因为样本数据,,,的均值,所以样本数据,,,的均值为,所以答案应填:.
考点:均值的性质.
10.1.6
【解析】设,,,,的平均数为,根据方差的计算公式有
.即,再利用,,,,的平均数为4求解.
【详解】依题意,得.
设,,,,的平均数为,
根据方差的计算公式有
.
,
即,
.
故答案为:1.6
【点睛】本题主要考查样本中的数字特征,还考查了数据处理和运算求解的能力,属于基础题.
11.
【分析】利用标准差和均值的公式完成计算.
【详解】设抽取的6个香囊中草药甲的含量分别为克,香囊功效分别为,.
草药甲的含量的平均数为6克,香囊功效的平均数为15,即,,
则,则这6个香囊中草药甲含量的方差
,
所以这6个香囊中草药甲含量的标准差为克.
故答案为:.
12.800
【详解】设C产品的数量为x件,则A产品的数量为1700-x件,由,各得C产品的数量为800件.
13.(1)580;438;908
(2),
【分析】(1)按照题目要求从给到的“随机数表”中从第二行的第三个数开始从左往右抽,每3个数字合为一个编号,需注意抽取的编号需要在成绩编号001—950的范围内;
(2)利用频率分布直方图的概率总和为1可计算的值,然后按照频率分布直方图中平均数的计算公式即可完成求解。
(1)
从给到的“随机数表”中从第二行的第三个数开始从左往右抽,依次是580,956,438,908,其中956不在给到的成绩编号001—950的范围内,故去掉,因此,前3个被抽到样本编号580,438,908;
(2)
由题意可知:,解得;
有频率分布直方图的平均数为:
,
故该校此次参赛学生成绩估计的平均分为71分.
14.(1);(2)19;(3) 购买1台机器的同时应购买19个易损零件.
【详解】试题分析:(Ⅰ)分x19及x>19,分别求解析式;(Ⅱ)通过频率大小进行比较;(Ⅲ)分别求出n=19,n=20时所需费用的平均数来确定.
试题解析:(Ⅰ)当时,;当时,,所以与的函数解析式为.
(Ⅱ)由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故的最小值为19.
(Ⅲ)若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3 800,20台的费用为4 300,10台的费用为4 800,因此这100台机器在购买易损零件上所需费用的平均数为.
若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4 000,10台的费用为4 500,因此这100台机器在购买易损零件上所需费用的平均数为.
比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
【考点】函数解析式、概率与统计
【名师点睛】本题把统计与函数结合在一起进行考查,有综合性但难度不大,求解的关键是读懂题意,所以提醒考生要重视数学中的阅读理解问题.
15.(1)53人;
(2)分钟.
【分析】(1)根据频率分布直方图,求出等待时间大于60分钟的频率即可计算作答.
(2)利用频率分布直方图求样本平均数的方法列式计算作答.
(1)
后三组的频率分别为0.35,0.15,0.03,
所以100名接种者中,等待时间大于60分钟的人数为人.
(2)
由频率分布直方图知:,解得,
所以等待时间的平均值为:
(分钟).
16.(1);(2)平均数为71,中位数为;(3)一等品有3个,二等品有2个.
【分析】(1)利用6组数据的频率和为1即可求出m的值;
(2)利用频率分布直方图求平均数和中位数的方法计算即得;
(3)利用分层抽样的抽样比计算即可作答.
【详解】(1)由,得,
所以直方图中m的值是0.030;
(2)平均数为,
因为,,
所以中位数在第4组,设中位数为n,则,解得,
所以可以估计该企业所生产口罩的质量指标值的平均数为71,中位数为;
(3)由频率分布直方图知:100个口罩中一等品、二等品各有60个、40个,
由分层抽样可知,所抽取的5个口罩中一等品有:(个),二等品有:(个),
所以抽取的5个口罩中一等品有3个,二等品有2个.
答案第1页,共2页
答案第1页,共2页
1.某大学为了解该校学生的体重情况,从中抽取了若干个样本进行研究,将数据整理后得到如图所示的频率分布直方图,已知图中从左到右前四组的频率之比为,其中第二组的频数为60,则下列说法错误的是( )
A.抽取的样本量为400
B.样本中体重在的频率为0.25
C.若该大学共有学生36000人,则体重超过的估计有600人
D.估计抽取的学生体重的中位数约为66
2.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
4.高三模拟考试常常划定的总分各批次分数线,通过一定的数学模型,确定不同学科在一本、二本等各批次“学科上线有双分”的分数线.考生总成绩达到总分各批次分数线的称为总分上线;考生某一单科成绩达到及学科上线有双分的称为单科上线.学科对总分的贡献或匹配程度评价有很大的意义.利用“学科对总分上线贡献率”和“学科有效分上线命中率”这两项评价指标,来反映各学科的单科成绩对考生总分上线的贡献与匹配程度,这对有效安排备考复习计划具有十分重要的意义.某州一诊考试划定总分一本线为465分,数学一本线为104分,某班一小组的总分和数学成绩如表,则该小组“数学学科对总分上线贡献率、有效分上线命中率”分别是( )(结果保留到小数点后一位有效数字)
学生编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
数学成绩 120 117 122 101 100 112 99 111 102 100 89 98 92 84 94 113 97 104 85 85
总分成绩 495 494 493 485 483 483 482 480 479 475 471 470 463 457 454 453 448 448 441 440
A.41.7%,71.4% B.60%,71.4%
C.41.7%,35% D.60%,35%
5.从分别写有的张卡片中随机抽取张,放回后再随机抽取张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
6.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
二、多选题
7.若数据x1,x2,…,xm的平均数为,方差为,数据y1,y2,…,yn的平均数为,方差为,下列说法中一定正确的有( )
A.这m+n个数据的平均数为
B.若这m+n个数据的平均数为ω,则这m+n个数据的方差为:
C.若m=n,,则
D.若m=n,,则
8.已知在一次射击预选赛中,甲 乙两人各射击次,两人成绩(所中环数越大,成绩越好)的频数分布表分别为:
环数
甲中频数
环数
乙中频数
下面判断正确的是( )A.甲所中环数的平均数大于乙所中环数的平均数
B.甲所中环数的中位数小于乙所中环数的中位数
C.甲所中环数的方差小于乙所中环数的方差
D.甲所中环数的方差大于乙所中环数的方差
三、填空题
9.已知样本数据,,,的均值,则样本数据,,,的均值为_______.
10.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产.设该工厂连续5天生产的口罩数依次为,,,,(单位:十万只),若这组数据,,,,的方差为1.44,且,,,,的平均数为4,则该工厂这5天平均每天生产口罩__________十万只.
11.佩香囊是端午节传统习俗之一,香囊内通常填充一些中草药,有清香、驱虫的功效.经研究发现一批香囊中一种草药甲的含量x(单位:克)与香囊功效y之间满足,现从中随机抽取了6个香囊,得到香囊中草药甲的含量的平均数为6克,香囊功效的平均数为15,则这6个香囊中草药甲含量的标准差为______克.
12.某企业三月中旬生产A、B、C三种产品共3000件,根据分层抽样的结果,企业统计员作了如下统计表格.
产品类别 A B C
产品数量(件) 1300
样本容量(件) 130
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是___________.
四、解答题
13.2020年1月8日,在“不忘初心 牢记使命”主题教育总结大会上,习总书记指出:“要把学习贯彻党的创新理论作为思想武装的重中之重,同学习党史 新中国史 改革开放史 社会主义发展史结合起来.”为了提高思想认识,某校开展了“学史明鉴 牢记使命”知识竞赛活动,从950名参赛的学生中随机选取100人的成绩作为样本,得到如图所示的频率分布直方图.
(1)现将全体参赛学生成绩编号为001--950,使用附图提供的“随机数表”从第二行的第三个数开始从左往右抽,请写出前3个被抽到样本编号;
(2)求频率分布直方图中的值,并估计该校此次参赛学生成绩的平均分(同一组数据用该组区间的中点值代表).
附图:
14.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),表示购机的同时购买的易损零件数.
(Ⅰ)若=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
15.2021年新冠疫情仍未平息,接种疫苗是防止新冠疫情最有效的手段今年5月,某地区疫苗接种出现了排长队现象,为了了解该地区接种人群的等待时间(从到达接种点到接种完成,不包括接种后的观察时间),随机调查了该地区某天接种的100人,制成了如下频率分布直方图.
(1)求样本中等待时间大于60分钟的人数;
(2)根据频率分布直方图,估计这100名接种者等待时间的平均值(各组区间的数据以该组区间的中间值作代表).
16.2021年3月18日,位于孝感市孝南区长兴工业园内的湖北福益康医疗科技有限公司正式落地投产,这是孝感市第一家获批的具有省级医疗器械生产许可证资质的企业,也是我市首家“一次性使用医用口罩、医用外科口罩”生产企业。在暑期新冠肺炎疫情反弹期间,该公司加班加点生产口罩、防护服,消毒水等防疫物品,保障抗疫一线医疗物资供应,在社会上赢得一片赞誉.在加大生产的同时,该公司狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:,,,…,,得到如下频率分布直方图.
(1)求出直方图中m的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表,中位数精确到);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,其中一等品和二等品分别有多少个.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据后四组的频率值可得前四组的频率之和,从而可求出第二组的频率,从而可求出抽取的样本量,故可判断选项A;
根据前四组的频率之和及前四组的频率之比为,可计算出体重在的频率,故可判断选项B;
通过样本中体重超过的频率可估计大学共有学生36000人时,体重超过的人数,从而可判断选项C;
利用频率分布直方图估计中位数的方法可计算出中位数,故可判断选项D.
【详解】由后四组的频率值可得前四组的频率之和为,
所以第二组的频率为,所以抽取的样本量为,故A正确;
体重在的频率为,B正确;
若该大学共有学生36000人,则体重超过的估计有人,C错误;
设抽取学生体重的中位数为,则,解得,D正确.
故选:C.
2.A
【分析】可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
【点睛】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
3.A
【分析】首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
4.A
【分析】由题知,双过线人数为5人,单过线人数为7人,总分过线人数为12人,进而根据题意求解即可;
【详解】解:由图表知双过线人数为5人,单过线人数为7人,总分过线人数为12人;
“学科对总分上线贡献率”为,
“学科有效分上线命中率”为,
故选:A.
【点睛】本题考查统计的应用,考查数据分析与处理能力,是中档题.本题解题的关键在于根据已知,读懂试题,在理解的基础上,进行数据分析处理计算.
5.D
【详解】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
基本事件总数n=5×5=25,
抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),
共有m=10个基本事件,
∴抽得的第一张卡片上的数大于第二张卡片上的数的概率p=
故答案为D.
6.C
【解析】根据图表中的数据的分析处理及进行简单的合情推理,逐一检验,即可求解.
【详解】由图表可知:
对于选项A中,2018年4月份我国新能源汽车的销量为8.2万辆,产量为8.1万辆,所以是正确的;
对于选项B中,2017年3月份我国新能源汽车的产量为万辆,所以是正确的;
对于选项C中,2019年2月份我国插电混合动力汽车的销量为万辆,所以不正确;
对于D中,2017年我国新能源汽车总销量为万辆,所以是正确的,
故选C.
【点睛】本题主要考查了对图表数据的分析处理,以及简单的合情推理的应用,其中解答中认真审题,根据图表的信息逐项判定是解答的关键,着重考查了推理与运算能力,属于基础题.
7.ABC
【分析】直接利用均值和方差的关系,方差和均值的性质,应用判断A,B,C,D的结论.
【详解】解:对于A,若数据x1,x2,…,xm的平均数为,数据y1,y2,…,yn的平均数为,
则m+n个数据的平均数为,故选项A正确;
对于B,由于m+n个数据的平均数为,若数据x1,x2,…,xm的方差为,数据y1,y2,…,yn的方差为,由方差的计算式得,这m+n个数据的方差为:,
又,所以,则, 所以
同理可得:,,
,故选项B正确;
对于C,若m=n,,则,故选项C正确;
对于D,若m=n,,则.
故选项D错误.
故选:ABC.
8.AC
【分析】根据随机变量的特征数据验证各选项得出答案.
【详解】解析:甲所中环数的平均数为
乙所中环数的平均数为:
所以甲所中环数的平均数大于乙所中环数的平均数,选项正确;
甲所中环数的中位数为:,乙所中环数的中位数为:
所以甲所中环数的中位数大于乙所中环数的中位数,选项B错误;甲所中环数的方差为:,乙所中环数的方差为:
所以乙所中环数的方差大于甲所中环数的方差,选项正确;选项错误.
故选:AC.
9.
【详解】因为样本数据,,,的均值,所以样本数据,,,的均值为,所以答案应填:.
考点:均值的性质.
10.1.6
【解析】设,,,,的平均数为,根据方差的计算公式有
.即,再利用,,,,的平均数为4求解.
【详解】依题意,得.
设,,,,的平均数为,
根据方差的计算公式有
.
,
即,
.
故答案为:1.6
【点睛】本题主要考查样本中的数字特征,还考查了数据处理和运算求解的能力,属于基础题.
11.
【分析】利用标准差和均值的公式完成计算.
【详解】设抽取的6个香囊中草药甲的含量分别为克,香囊功效分别为,.
草药甲的含量的平均数为6克,香囊功效的平均数为15,即,,
则,则这6个香囊中草药甲含量的方差
,
所以这6个香囊中草药甲含量的标准差为克.
故答案为:.
12.800
【详解】设C产品的数量为x件,则A产品的数量为1700-x件,由,各得C产品的数量为800件.
13.(1)580;438;908
(2),
【分析】(1)按照题目要求从给到的“随机数表”中从第二行的第三个数开始从左往右抽,每3个数字合为一个编号,需注意抽取的编号需要在成绩编号001—950的范围内;
(2)利用频率分布直方图的概率总和为1可计算的值,然后按照频率分布直方图中平均数的计算公式即可完成求解。
(1)
从给到的“随机数表”中从第二行的第三个数开始从左往右抽,依次是580,956,438,908,其中956不在给到的成绩编号001—950的范围内,故去掉,因此,前3个被抽到样本编号580,438,908;
(2)
由题意可知:,解得;
有频率分布直方图的平均数为:
,
故该校此次参赛学生成绩估计的平均分为71分.
14.(1);(2)19;(3) 购买1台机器的同时应购买19个易损零件.
【详解】试题分析:(Ⅰ)分x19及x>19,分别求解析式;(Ⅱ)通过频率大小进行比较;(Ⅲ)分别求出n=19,n=20时所需费用的平均数来确定.
试题解析:(Ⅰ)当时,;当时,,所以与的函数解析式为.
(Ⅱ)由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故的最小值为19.
(Ⅲ)若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3 800,20台的费用为4 300,10台的费用为4 800,因此这100台机器在购买易损零件上所需费用的平均数为.
若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4 000,10台的费用为4 500,因此这100台机器在购买易损零件上所需费用的平均数为.
比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
【考点】函数解析式、概率与统计
【名师点睛】本题把统计与函数结合在一起进行考查,有综合性但难度不大,求解的关键是读懂题意,所以提醒考生要重视数学中的阅读理解问题.
15.(1)53人;
(2)分钟.
【分析】(1)根据频率分布直方图,求出等待时间大于60分钟的频率即可计算作答.
(2)利用频率分布直方图求样本平均数的方法列式计算作答.
(1)
后三组的频率分别为0.35,0.15,0.03,
所以100名接种者中,等待时间大于60分钟的人数为人.
(2)
由频率分布直方图知:,解得,
所以等待时间的平均值为:
(分钟).
16.(1);(2)平均数为71,中位数为;(3)一等品有3个,二等品有2个.
【分析】(1)利用6组数据的频率和为1即可求出m的值;
(2)利用频率分布直方图求平均数和中位数的方法计算即得;
(3)利用分层抽样的抽样比计算即可作答.
【详解】(1)由,得,
所以直方图中m的值是0.030;
(2)平均数为,
因为,,
所以中位数在第4组,设中位数为n,则,解得,
所以可以估计该企业所生产口罩的质量指标值的平均数为71,中位数为;
(3)由频率分布直方图知:100个口罩中一等品、二等品各有60个、40个,
由分层抽样可知,所抽取的5个口罩中一等品有:(个),二等品有:(个),
所以抽取的5个口罩中一等品有3个,二等品有2个.
答案第1页,共2页
答案第1页,共2页
