高中数学人教B版(2019)必修第二册节节通关练——5.1统计A(含解析)
文档属性
| 名称 | 高中数学人教B版(2019)必修第二册节节通关练——5.1统计A(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 400.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 09:55:33 | ||
图片预览



文档简介
一、单选题
1.在以下调查中,适合用全面调查的是( )
A.调查某企业的产品在全国市场的占有率
B.了解一个班级学生的近视程度
C.了解某地区的空气质量
D.调查一个大型水库所有鱼中鲫鱼所占的比例
2.以下数据为参加数学竞赛决赛的人的成绩:(单位:分)、、、、、、、、、、、、、、,则这人成绩的第百分位数是
A. B. C. D.
3.某单位共有老年、中年、青年职工320人,其中老年、中年、青年职工的人数之比为7∶10∶15.为了了解职工的身体状况,现采用分层抽样方法进行调查,抽取的样本中有青年职工30人,则抽取的老年职工的人数为( )
A.14 B.20 C.21 D.70
4.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
5.3月12日是植树节,某地区有375人参与植树,植树的树种及数量的折线图如图所示.植树后,该地区农业局根据树种用分层抽样的方法抽取75棵树,请专业人士查看植树的情况,则被抽取的柳树的棵数为( )
A.20 B.25 C.40 D.50
6.我国冰雪健儿自1992年实现冬奥奖牌数0的突破,到北京冬奥会结束,共获得77块奖牌.现将1992年以来我国冬奥会获得奖牌数量统计如下表:
年份 1992 1994 1998 2002 2006 2010 2014 2018 2022
奖牌数 3 3 8 8 11 11 9 9 15
则1992年以来我国获得奖牌数的中位数为( )A.8 B.9 C.10 D.11
二、多选题
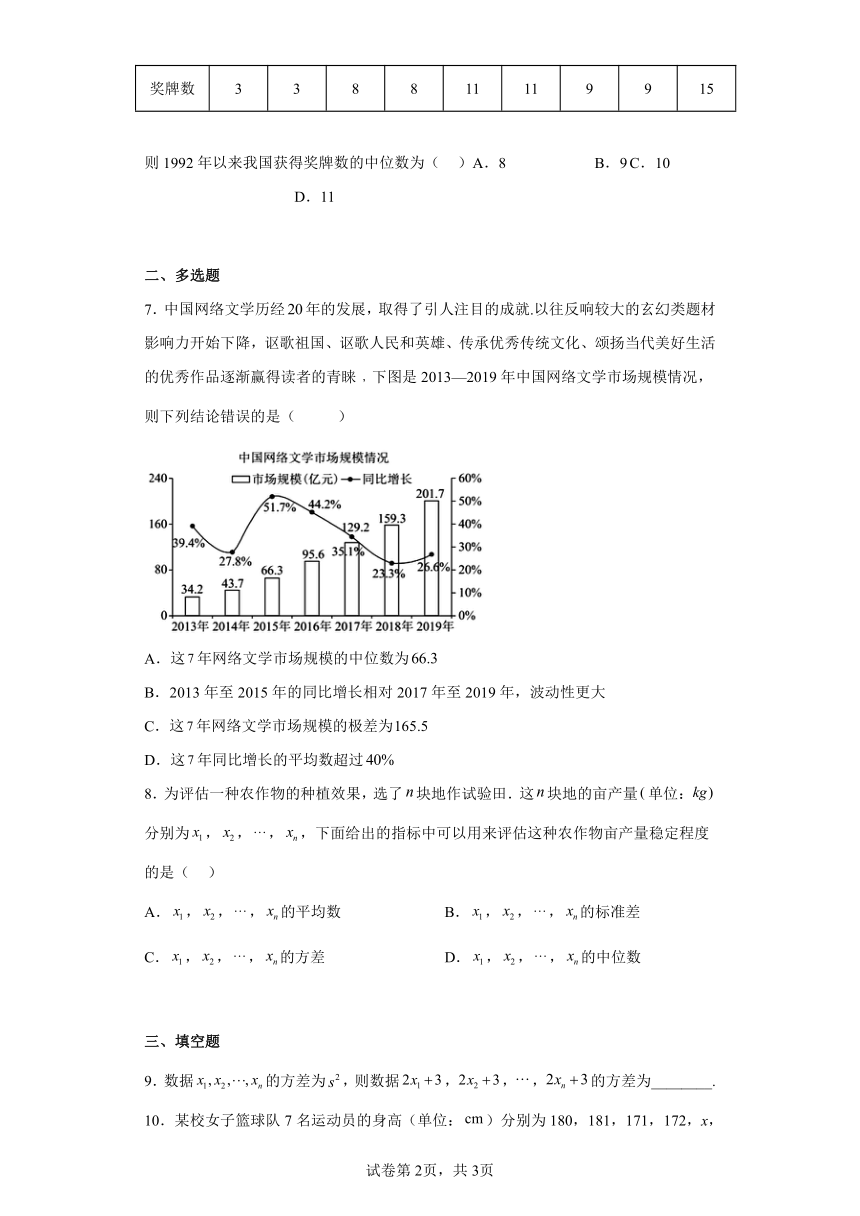
7.中国网络文学历经年的发展,取得了引人注目的成就.以往反响较大的玄幻类题材影响力开始下降,讴歌祖国、讴歌人民和英雄、传承优秀传统文化、颂扬当代美好生活的优秀作品逐渐赢得读者的青睐﹐下图是2013—2019年中国网络文学市场规模情况,则下列结论错误的是( )
A.这年网络文学市场规模的中位数为
B.2013年至2015年的同比增长相对2017年至2019年,波动性更大
C.这年网络文学市场规模的极差为
D.这年同比增长的平均数超过
8.为评估一种农作物的种植效果,选了块地作试验田.这块地的亩产量单位:分别为,,,,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.,,,的平均数 B.,,,的标准差
C.,,,的方差 D.,,,的中位数
三、填空题
9.数据的方差为,则数据,,,的方差为________.
10.某校女子篮球队7名运动员的身高(单位:)分别为180,181,171,172,x,174,175,已知记录的平均身高为175,但记录中有一名运动员身高因记录不清,而用x代替,那么x的值为__________.
11.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________ 件.
12.在容量为100的总体中用随机数表法抽取5个样本,总体编号为,给出下列几组号码:
①00,01,02,03,04;
②10,30,50,70,90;
③49,19,46,04,67;
④11,22,33,44,55.
则可能成为所得样本编号的是________(填相应序号).
四、解答题
13.给出下列两组数据:甲:12,13,11,10,14.乙:10,17,10,13,10.
(1)分别计算两组数据的平均差,并根据计算结果判断哪组数据波动大.
(2)分别计算两组数据的方差,并根据计算结果判断哪组数据波动大.
(3)以上两种判断方法的结果是否一致?
14.求一次函数在区间()上的平均变化率.
15.图①和图②是某单位的各项支出情况,根据图中提供的信息,回答下列问题:
(1)2018年管理费支出的金额是多少?
(2)2018年总支出比2017年增加多少?增加了百分之几?
16.有一个袋子中装有大小相同、质量相等的小球30个,其中红球25个,白球5个.每次抽取4个球观察颜色.如果使用简单随机抽样,应当如何编号?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据调查的范围,从经济性层面判断是否适合全面调查.
【详解】A、C、D由调查范围较广,调查的经济成本高,不适合全面调查,
B班级学生样本数量小,故适合全面调查.
故选:B
2.D
【分析】将数据由小到大依次排列,找出第个数,可得出这人成绩的第百分位数.
【详解】将这人成绩由小到大依次排列为、、、、、、、、、、、、、、,
,因此,这人成绩的第百分位数是.
故选:D.
【点睛】本题考查百分位数的计算,熟悉百分位数的定义是计算的关键,考查计算能力,属于基础题.
3.A
【分析】根据给定条件利用分层抽样的定义直接列式计算即可判断作答.
【详解】因老年、中年、青年职工的人数之比为7∶10∶15,而抽取的样本中有青年职工30人,
于是,设抽取的老年职工的人数为x,则x∶30=7∶15,解得x=14,
所以抽取的老年职工的人数为14.
故选:A
4.B
【详解】评估这种农作物亩产量稳定程度的指标是标准差或方差,故选B.
点睛:众数:一组数据出现次数最多的数叫众数,众数反映一组数据的多数水平;
中位数:一组数据中间的数(起到分水岭的作用),中位数反映一组数据的中间水平;
平均数:反映一组数据的平均水平;
方差:反映一组数据偏离平均数的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
标准差是方差的算术平方根,意义在于反映一组数据的离散程度.
5.B
【分析】根据分层抽样的等比例性质,结合折线图求抽取75棵树中柳树的棵数即可.
【详解】依题意,被抽取的柳树的棵数为棵.
故选:B
6.B
【分析】把数表中的奖牌数从小到大排列即可求出中位数.
【详解】将自1992年以来我国冬奥会获得奖牌数从小到大排列为:3,3,8,8,9,9,11,11,15,
所以1992年以来我国获得奖牌数的中位数为9.
故选:B
7.ACD
【分析】由条形图、折线图及中位数的定义直接判断A、B;根据极差、平均数的求法求极差和平均数判断C、D.
【详解】由条形图知﹐这7年网络文学市场规模的中位数为,故A错误﹔
由折线图知:2013年至2015年的同比增长相对2017年至2019年,波动性更大,故B正确,
这年网络文学市场规模的极差为故C错误,
这年同比增长的平均数为
故D错误.
故选:ACD.
8.BC
【分析】利用平均数、标准差、方差、中位数的定义和意义对各选项直接一一判断即可.
【详解】在A中,平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标,
故A不可以用来评估这种农作物亩产量稳定程度;
在B中,标准差能反映一个数据集的离散程度,故B可以用来评估这种农作物亩产量稳定程度;
在C中,方差能反映一个数据集的离散程度,故C可以用来评估这种农作物亩产量稳定程度;
在D中,中位数将数据分成前半部分和后半部分,用来代表一组数据的“中等水平”,
故D不可以用来评估这种农作物亩产量稳定程度.
故选:BC.
9.
【分析】直接利用方差公式求解即可.
【详解】解:设的平均数为,则,,,为,
所以,,,的方差为:
.
故答案为:
【点睛】此题考查方差的计算,考查计算能力,属于基础题.
10.172
【分析】利用样本平均数公式,即可计算.
【详解】由条件可知,
解得:.
故答案为:172
11.18
【详解】应从丙种型号的产品中抽取件,故答案为18.
点睛:在分层抽样的过程中,为了保证每个个体被抽到的可能性是相同的,这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比,即ni∶Ni=n∶N.
12.①②③④
【解析】根据简单抽样的定义和随机数法直接判断即可.
【详解】解析:随机数表法是一种简单随机抽样方法,因此每一个个体都有可能被抽到,且被抽到的可能性相同,因此所列几组都可能成为所得样本的编号.
答案:①②③④
【点睛】本题考查了简单随机抽样的定义和随机数法,属于基础题.
13.(1)甲,乙的平均差分别为1.2,2.4,乙组数据波动较大;(2)甲,乙的方差分别为2,7.6,乙组数据波动较大;(3)两种判断方法的结果一致
【解析】(1)先求出甲、乙的平均数,再计算平均差,判断哪组数据波动大;(2)直接利用方差的公式求方差,再判断哪组数据波动大;(3)根据前面计算结果判断得解.
【详解】(1)由已知可得,.
甲的平均差:,
乙的平均差:.
乙的平均差较大,因此乙组数据波动较大。
(2),
.
所以乙的方差较大,因此乙组数据波动较大.
(3)两种判断方法的结果一致.
【点睛】本题主要考查平均数和平均差的计算,考查方差的计算和意义,意在考查学生对这些知识的理解掌握水平.
14.
【分析】分别计算,,再计算即可求解.
【详解】因为,
,
所以在区间()上的平均变化率为:
,
所以一次函数在上的平均变化率为.
15.(1)2万元;
(2)2万元,,
【分析】(1)根据条形图可得2018年的总支出,结合扇形图可得管理费支出的比例,即得;
(2)由题可得2018年总支出比2017年的增加量,进而即得.
(1)
根据条形图可得2018年的总支出为8万元,
根据扇形图可得管理费占总支出的,
所以2018年管理费支出的金额为(万元);
(2)
由图可知2018年总支出比2017年增加了(万元),
比2017年增加了.
16.答案见解析.
【分析】将30个小球依次编号即可.
【详解】将25个红球编号为红球1,红球2,,红球25,白球编号为白球26,,白球30.
答案第1页,共2页
答案第1页,共2页
1.在以下调查中,适合用全面调查的是( )
A.调查某企业的产品在全国市场的占有率
B.了解一个班级学生的近视程度
C.了解某地区的空气质量
D.调查一个大型水库所有鱼中鲫鱼所占的比例
2.以下数据为参加数学竞赛决赛的人的成绩:(单位:分)、、、、、、、、、、、、、、,则这人成绩的第百分位数是
A. B. C. D.
3.某单位共有老年、中年、青年职工320人,其中老年、中年、青年职工的人数之比为7∶10∶15.为了了解职工的身体状况,现采用分层抽样方法进行调查,抽取的样本中有青年职工30人,则抽取的老年职工的人数为( )
A.14 B.20 C.21 D.70
4.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
5.3月12日是植树节,某地区有375人参与植树,植树的树种及数量的折线图如图所示.植树后,该地区农业局根据树种用分层抽样的方法抽取75棵树,请专业人士查看植树的情况,则被抽取的柳树的棵数为( )
A.20 B.25 C.40 D.50
6.我国冰雪健儿自1992年实现冬奥奖牌数0的突破,到北京冬奥会结束,共获得77块奖牌.现将1992年以来我国冬奥会获得奖牌数量统计如下表:
年份 1992 1994 1998 2002 2006 2010 2014 2018 2022
奖牌数 3 3 8 8 11 11 9 9 15
则1992年以来我国获得奖牌数的中位数为( )A.8 B.9 C.10 D.11
二、多选题
7.中国网络文学历经年的发展,取得了引人注目的成就.以往反响较大的玄幻类题材影响力开始下降,讴歌祖国、讴歌人民和英雄、传承优秀传统文化、颂扬当代美好生活的优秀作品逐渐赢得读者的青睐﹐下图是2013—2019年中国网络文学市场规模情况,则下列结论错误的是( )
A.这年网络文学市场规模的中位数为
B.2013年至2015年的同比增长相对2017年至2019年,波动性更大
C.这年网络文学市场规模的极差为
D.这年同比增长的平均数超过
8.为评估一种农作物的种植效果,选了块地作试验田.这块地的亩产量单位:分别为,,,,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.,,,的平均数 B.,,,的标准差
C.,,,的方差 D.,,,的中位数
三、填空题
9.数据的方差为,则数据,,,的方差为________.
10.某校女子篮球队7名运动员的身高(单位:)分别为180,181,171,172,x,174,175,已知记录的平均身高为175,但记录中有一名运动员身高因记录不清,而用x代替,那么x的值为__________.
11.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________ 件.
12.在容量为100的总体中用随机数表法抽取5个样本,总体编号为,给出下列几组号码:
①00,01,02,03,04;
②10,30,50,70,90;
③49,19,46,04,67;
④11,22,33,44,55.
则可能成为所得样本编号的是________(填相应序号).
四、解答题
13.给出下列两组数据:甲:12,13,11,10,14.乙:10,17,10,13,10.
(1)分别计算两组数据的平均差,并根据计算结果判断哪组数据波动大.
(2)分别计算两组数据的方差,并根据计算结果判断哪组数据波动大.
(3)以上两种判断方法的结果是否一致?
14.求一次函数在区间()上的平均变化率.
15.图①和图②是某单位的各项支出情况,根据图中提供的信息,回答下列问题:
(1)2018年管理费支出的金额是多少?
(2)2018年总支出比2017年增加多少?增加了百分之几?
16.有一个袋子中装有大小相同、质量相等的小球30个,其中红球25个,白球5个.每次抽取4个球观察颜色.如果使用简单随机抽样,应当如何编号?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据调查的范围,从经济性层面判断是否适合全面调查.
【详解】A、C、D由调查范围较广,调查的经济成本高,不适合全面调查,
B班级学生样本数量小,故适合全面调查.
故选:B
2.D
【分析】将数据由小到大依次排列,找出第个数,可得出这人成绩的第百分位数.
【详解】将这人成绩由小到大依次排列为、、、、、、、、、、、、、、,
,因此,这人成绩的第百分位数是.
故选:D.
【点睛】本题考查百分位数的计算,熟悉百分位数的定义是计算的关键,考查计算能力,属于基础题.
3.A
【分析】根据给定条件利用分层抽样的定义直接列式计算即可判断作答.
【详解】因老年、中年、青年职工的人数之比为7∶10∶15,而抽取的样本中有青年职工30人,
于是,设抽取的老年职工的人数为x,则x∶30=7∶15,解得x=14,
所以抽取的老年职工的人数为14.
故选:A
4.B
【详解】评估这种农作物亩产量稳定程度的指标是标准差或方差,故选B.
点睛:众数:一组数据出现次数最多的数叫众数,众数反映一组数据的多数水平;
中位数:一组数据中间的数(起到分水岭的作用),中位数反映一组数据的中间水平;
平均数:反映一组数据的平均水平;
方差:反映一组数据偏离平均数的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
标准差是方差的算术平方根,意义在于反映一组数据的离散程度.
5.B
【分析】根据分层抽样的等比例性质,结合折线图求抽取75棵树中柳树的棵数即可.
【详解】依题意,被抽取的柳树的棵数为棵.
故选:B
6.B
【分析】把数表中的奖牌数从小到大排列即可求出中位数.
【详解】将自1992年以来我国冬奥会获得奖牌数从小到大排列为:3,3,8,8,9,9,11,11,15,
所以1992年以来我国获得奖牌数的中位数为9.
故选:B
7.ACD
【分析】由条形图、折线图及中位数的定义直接判断A、B;根据极差、平均数的求法求极差和平均数判断C、D.
【详解】由条形图知﹐这7年网络文学市场规模的中位数为,故A错误﹔
由折线图知:2013年至2015年的同比增长相对2017年至2019年,波动性更大,故B正确,
这年网络文学市场规模的极差为故C错误,
这年同比增长的平均数为
故D错误.
故选:ACD.
8.BC
【分析】利用平均数、标准差、方差、中位数的定义和意义对各选项直接一一判断即可.
【详解】在A中,平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标,
故A不可以用来评估这种农作物亩产量稳定程度;
在B中,标准差能反映一个数据集的离散程度,故B可以用来评估这种农作物亩产量稳定程度;
在C中,方差能反映一个数据集的离散程度,故C可以用来评估这种农作物亩产量稳定程度;
在D中,中位数将数据分成前半部分和后半部分,用来代表一组数据的“中等水平”,
故D不可以用来评估这种农作物亩产量稳定程度.
故选:BC.
9.
【分析】直接利用方差公式求解即可.
【详解】解:设的平均数为,则,,,为,
所以,,,的方差为:
.
故答案为:
【点睛】此题考查方差的计算,考查计算能力,属于基础题.
10.172
【分析】利用样本平均数公式,即可计算.
【详解】由条件可知,
解得:.
故答案为:172
11.18
【详解】应从丙种型号的产品中抽取件,故答案为18.
点睛:在分层抽样的过程中,为了保证每个个体被抽到的可能性是相同的,这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比,即ni∶Ni=n∶N.
12.①②③④
【解析】根据简单抽样的定义和随机数法直接判断即可.
【详解】解析:随机数表法是一种简单随机抽样方法,因此每一个个体都有可能被抽到,且被抽到的可能性相同,因此所列几组都可能成为所得样本的编号.
答案:①②③④
【点睛】本题考查了简单随机抽样的定义和随机数法,属于基础题.
13.(1)甲,乙的平均差分别为1.2,2.4,乙组数据波动较大;(2)甲,乙的方差分别为2,7.6,乙组数据波动较大;(3)两种判断方法的结果一致
【解析】(1)先求出甲、乙的平均数,再计算平均差,判断哪组数据波动大;(2)直接利用方差的公式求方差,再判断哪组数据波动大;(3)根据前面计算结果判断得解.
【详解】(1)由已知可得,.
甲的平均差:,
乙的平均差:.
乙的平均差较大,因此乙组数据波动较大。
(2),
.
所以乙的方差较大,因此乙组数据波动较大.
(3)两种判断方法的结果一致.
【点睛】本题主要考查平均数和平均差的计算,考查方差的计算和意义,意在考查学生对这些知识的理解掌握水平.
14.
【分析】分别计算,,再计算即可求解.
【详解】因为,
,
所以在区间()上的平均变化率为:
,
所以一次函数在上的平均变化率为.
15.(1)2万元;
(2)2万元,,
【分析】(1)根据条形图可得2018年的总支出,结合扇形图可得管理费支出的比例,即得;
(2)由题可得2018年总支出比2017年的增加量,进而即得.
(1)
根据条形图可得2018年的总支出为8万元,
根据扇形图可得管理费占总支出的,
所以2018年管理费支出的金额为(万元);
(2)
由图可知2018年总支出比2017年增加了(万元),
比2017年增加了.
16.答案见解析.
【分析】将30个小球依次编号即可.
【详解】将25个红球编号为红球1,红球2,,红球25,白球编号为白球26,,白球30.
答案第1页,共2页
答案第1页,共2页
