14.1.1同底数幂的乘法 课件(共21张PPT)
文档属性
| 名称 | 14.1.1同底数幂的乘法 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 10:48:48 | ||
图片预览







文档简介
(共21张PPT)
14.1.1 同底数幂的乘法
人教版八年级上册
知识回顾
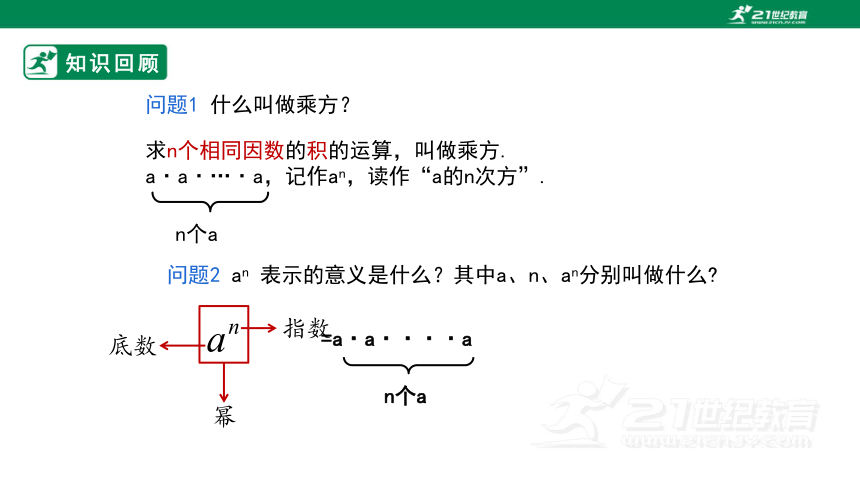
指数
底数
幂
问题1 什么叫做乘方?
求n个相同因数的积的运算,叫做乘方.
a·a·…·a,记作an,读作“a的n次方”.
n个a
=a·a····a
n个a
问题2 an 表示的意义是什么?其中a、n、an分别叫做什么
知识回顾
请按照幂的定义填空.
23 =____________;
102×102×102×102×102×102=_______;
(-a)3的底数是_____,指数是____;
(b-a)4的底数是______,指数是____.
2×2×2
3
4
-a
b-a
1026
教学目标
1.理解同底数幂的乘法的性质,会利用这一性质进行同底数幂的乘法运算.
2.掌握同底数幂的乘法的运算性质的推导.
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
新知导入
思考:一种电子计算机每秒可进行1千万亿( 1015 )次运算,它工作103秒可进行多少次运算?
它工作103秒可进行运算的次数为1015×103.
怎样计算1015×103呢?
=10×10×10×10×10×…×10×10
新知探究
根据乘方的意义可知
1015×103
15个10
18个10
=1018 .
=(10×10×…×10×10)
×(10×10×10)
知识点 1
同底数幂的乘法法则
新知探究
根据乘方的意义填空(m,n是正整数):
(1) 32×33=3( );
(2) (-4)3×(-4)4=(-4)( );
(3) a3×a5 =a( );
(4) 3m×3n=3( );
(5) (-4)m×(-4)n=(-4)( ).
5
7
8
m+n
m+n
观察计算结果,你能发现什么规律呢?
新知探究
猜想: am · an= (m、n都是正整数)
am+n
am · an =
(a×a…a)
m个a
(a×a…a)
n个a
(乘方的意义)
= a×a…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
即
am · an = am+n (当m、n都是正整数)
猜想与证明
新知探究
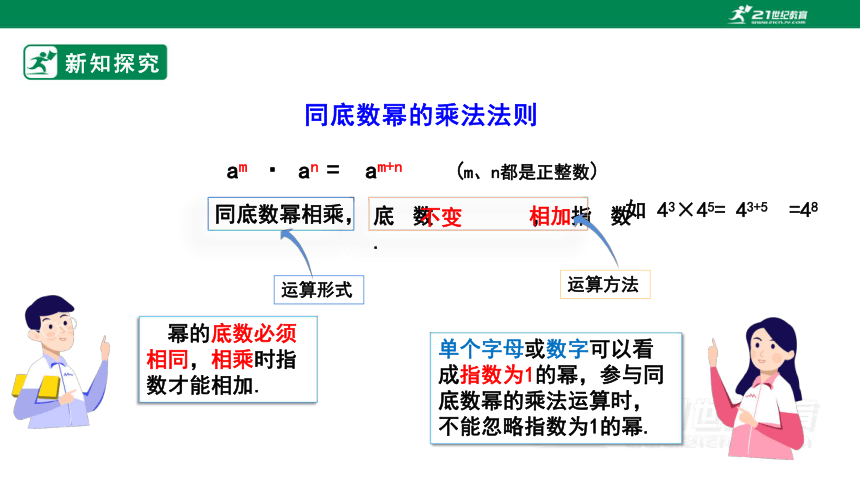
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 .
不变
相加
运算形式
运算方法
幂的底数必须相同,相乘时指数才能相加.
如 43×45=
43+5
=48
同底数幂的乘法法则
单个字母或数字可以看成指数为1的幂,参与同底数幂的乘法运算时,不能忽略指数为1的幂.
新知典例
例 计算:
(1) x2·x5; (2) a·a6;
(3) (-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解:(1) x2·x5=x2+5=x7;
(2) a·a6=a1+6=a7;
(3) (-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8=256;
(4) xm·x3m+1=xm+3m+1=x4m+1.
a的指数为1
新知探究
拓展:(1)同底数幂的乘法的性质也适用于三个及三个以上的同底数幂相乘,即 am an ap = am+n+p(m, n, p都为正整数).
(2)同底数幂的乘法的性质可以逆用,即 am+n = am an (m,n都为正整数).
(3)在幂的运算中,经常用到以下变形:
am (m为正偶数),
-am (m为正奇数).
①(-a)m
(b-a)m (m为正偶数) ,
-(b-a)m (m为正奇数).
②(a-b)m
新知小结
(1)同底数幂相乘时,底数可以是单项式,也可以是多项式.
(2)底数不同时,若能化成相同底数,则先化成相同底数,再利用同底数幂的乘法的性质计算.
am · an = am+n (m、n都是正整数)
课堂练习
1.下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
×
b5 · b5= b10
×
b5 + b5 = 2b5
×
x5 · x5 = x10
×
y5 · y5 =y10
×
c · c3 = c4
×
m + m3 = m + m3
课堂练习
(3) -x2 (-x)8 = -x2 x8= -x10 ;
(2) (-10)3×(-10)5 =(-10)3+5=(-10)8 ;
2.计算:(1) x7 x ; (2) (-10)3×(-10)5 ;
(3) -x2 (-x)8 ; (4) (x-3y)3 (x-3y)2 (x-3y) ;
解:(1) x7 x=x7+1=x8 ;
(4) (x-3y)3 (x-3y)2 (x-3y)=(x-3y)3+2+1=(x-3y)6.
课堂练习
3.已知xm=8,xn=9,求xm+n 的值.
xm+n = xm xn (m, n, p都为正整数)
xm xn= xm+n (m, n, p都为正整数)
当指数是和的形式时,考虑逆用同底数幂的乘法的性质
思路引导:
解:xm+n = xm xn=8×9=72.
课堂练习
4.(2020·河南)电子文件的大小常用B,KB,MB,GB等作为单位,其中1 GB=210 MB,1 MB=210 KB,1 KB= 210 B.某视频文件的大小约为1 GB,1 GB等于( )
A. 230 B
B. 830 B
C. 8×1010 B
D. 2×1030 B
A
210×210×210=210+10+10=230
课堂练习
5. 计算(b-a)3 (a-b)n.
解:原式=-(a-b)3 (a-b)n
=-(a-b)n+3
课堂练习
解:
6.如果 7m+n 能被16整除,试说明 7m+2+n 也能被16整除.
分析:判断一个式子能否被一个数整除,只需看这个式子能否化成这个数与另一个式子的乘积形式.
因为7m+2+n =72 7m+n=49×7m+n=48×7m+7m+n ,
且7m+n和48×7m都能被16整除,
所以 48×7m+7m+n也能被16整除.
即 7m+2+n 也能被16整除.
课堂总结
同底数幂
的乘法
性质:同底数幂相乘,底数不变,指数相加.
am·an=am+n (m,n为正整数)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.1.1 同底数幂的乘法
人教版八年级上册
知识回顾
指数
底数
幂
问题1 什么叫做乘方?
求n个相同因数的积的运算,叫做乘方.
a·a·…·a,记作an,读作“a的n次方”.
n个a
=a·a····a
n个a
问题2 an 表示的意义是什么?其中a、n、an分别叫做什么
知识回顾
请按照幂的定义填空.
23 =____________;
102×102×102×102×102×102=_______;
(-a)3的底数是_____,指数是____;
(b-a)4的底数是______,指数是____.
2×2×2
3
4
-a
b-a
1026
教学目标
1.理解同底数幂的乘法的性质,会利用这一性质进行同底数幂的乘法运算.
2.掌握同底数幂的乘法的运算性质的推导.
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
新知导入
思考:一种电子计算机每秒可进行1千万亿( 1015 )次运算,它工作103秒可进行多少次运算?
它工作103秒可进行运算的次数为1015×103.
怎样计算1015×103呢?
=10×10×10×10×10×…×10×10
新知探究
根据乘方的意义可知
1015×103
15个10
18个10
=1018 .
=(10×10×…×10×10)
×(10×10×10)
知识点 1
同底数幂的乘法法则
新知探究
根据乘方的意义填空(m,n是正整数):
(1) 32×33=3( );
(2) (-4)3×(-4)4=(-4)( );
(3) a3×a5 =a( );
(4) 3m×3n=3( );
(5) (-4)m×(-4)n=(-4)( ).
5
7
8
m+n
m+n
观察计算结果,你能发现什么规律呢?
新知探究
猜想: am · an= (m、n都是正整数)
am+n
am · an =
(a×a…a)
m个a
(a×a…a)
n个a
(乘方的意义)
= a×a…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
即
am · an = am+n (当m、n都是正整数)
猜想与证明
新知探究
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 .
不变
相加
运算形式
运算方法
幂的底数必须相同,相乘时指数才能相加.
如 43×45=
43+5
=48
同底数幂的乘法法则
单个字母或数字可以看成指数为1的幂,参与同底数幂的乘法运算时,不能忽略指数为1的幂.
新知典例
例 计算:
(1) x2·x5; (2) a·a6;
(3) (-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解:(1) x2·x5=x2+5=x7;
(2) a·a6=a1+6=a7;
(3) (-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8=256;
(4) xm·x3m+1=xm+3m+1=x4m+1.
a的指数为1
新知探究
拓展:(1)同底数幂的乘法的性质也适用于三个及三个以上的同底数幂相乘,即 am an ap = am+n+p(m, n, p都为正整数).
(2)同底数幂的乘法的性质可以逆用,即 am+n = am an (m,n都为正整数).
(3)在幂的运算中,经常用到以下变形:
am (m为正偶数),
-am (m为正奇数).
①(-a)m
(b-a)m (m为正偶数) ,
-(b-a)m (m为正奇数).
②(a-b)m
新知小结
(1)同底数幂相乘时,底数可以是单项式,也可以是多项式.
(2)底数不同时,若能化成相同底数,则先化成相同底数,再利用同底数幂的乘法的性质计算.
am · an = am+n (m、n都是正整数)
课堂练习
1.下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
×
b5 · b5= b10
×
b5 + b5 = 2b5
×
x5 · x5 = x10
×
y5 · y5 =y10
×
c · c3 = c4
×
m + m3 = m + m3
课堂练习
(3) -x2 (-x)8 = -x2 x8= -x10 ;
(2) (-10)3×(-10)5 =(-10)3+5=(-10)8 ;
2.计算:(1) x7 x ; (2) (-10)3×(-10)5 ;
(3) -x2 (-x)8 ; (4) (x-3y)3 (x-3y)2 (x-3y) ;
解:(1) x7 x=x7+1=x8 ;
(4) (x-3y)3 (x-3y)2 (x-3y)=(x-3y)3+2+1=(x-3y)6.
课堂练习
3.已知xm=8,xn=9,求xm+n 的值.
xm+n = xm xn (m, n, p都为正整数)
xm xn= xm+n (m, n, p都为正整数)
当指数是和的形式时,考虑逆用同底数幂的乘法的性质
思路引导:
解:xm+n = xm xn=8×9=72.
课堂练习
4.(2020·河南)电子文件的大小常用B,KB,MB,GB等作为单位,其中1 GB=210 MB,1 MB=210 KB,1 KB= 210 B.某视频文件的大小约为1 GB,1 GB等于( )
A. 230 B
B. 830 B
C. 8×1010 B
D. 2×1030 B
A
210×210×210=210+10+10=230
课堂练习
5. 计算(b-a)3 (a-b)n.
解:原式=-(a-b)3 (a-b)n
=-(a-b)n+3
课堂练习
解:
6.如果 7m+n 能被16整除,试说明 7m+2+n 也能被16整除.
分析:判断一个式子能否被一个数整除,只需看这个式子能否化成这个数与另一个式子的乘积形式.
因为7m+2+n =72 7m+n=49×7m+n=48×7m+7m+n ,
且7m+n和48×7m都能被16整除,
所以 48×7m+7m+n也能被16整除.
即 7m+2+n 也能被16整除.
课堂总结
同底数幂
的乘法
性质:同底数幂相乘,底数不变,指数相加.
am·an=am+n (m,n为正整数)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
