2021-2022学年八年级下册数学鲁教版(五四学制)第六章特殊平行四边形 单元检测卷(含答案)
文档属性
| 名称 | 2021-2022学年八年级下册数学鲁教版(五四学制)第六章特殊平行四边形 单元检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 238.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 20:35:32 | ||
图片预览



文档简介
单元试卷 第六章
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列命题是真命题的是( )
(A)对角线相等的四边形是矩形
(B)对角线互相垂直的四边形是矩形
(C)对角线互相垂直的矩形是正方形
(D)四边相等的平行四边形是正方形
2.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
第2题图
(A)∠ABC=90° (B)AC=BD (C)OA=OB (D)OA=AD
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( )
第3题图
(A)AB=BC (B)AC=BC (C)∠B=60° (D)∠ACB=60°
4.如图,菱形ABCD的对角线AC与BD交于点O,E是DC边的中点,连接OE,若OE=5,BD=12,则菱形的面积为( )
第4题图
(A)96 (B)48 (C)192 (D)24
5.一个矩形的三个顶点在平面直角坐标系中的坐标分别为(-1,-2),
(3,-2),(3,1),则第四个顶点的坐标为( )
(A)(-1,1) (B)(1,-1) (C)(-1,2) (D)(1,1)
6.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( )
(A)DA=DE (B)∠ABC=2∠E (C)∠EAC=90° (D)BD=CE
第6题图
7.如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连接DM,DN,MN.若AB=6,则DN的长为( )
第7题图
(A)1 (B)2 (C)3 (D)4
8.如图1为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队,如果将每位队员看成一个点,队形可近似看成由图2所示的若干个正方形拼成的图形,其中与△ABC全等的三角形是( )
第8题图
(A)△AEG (B)△ADF (C)△DFG (D)△CEG
9.如图,E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.正确的个数是( )
第9题图
(A)1 (B)2 (C)3 (D)4
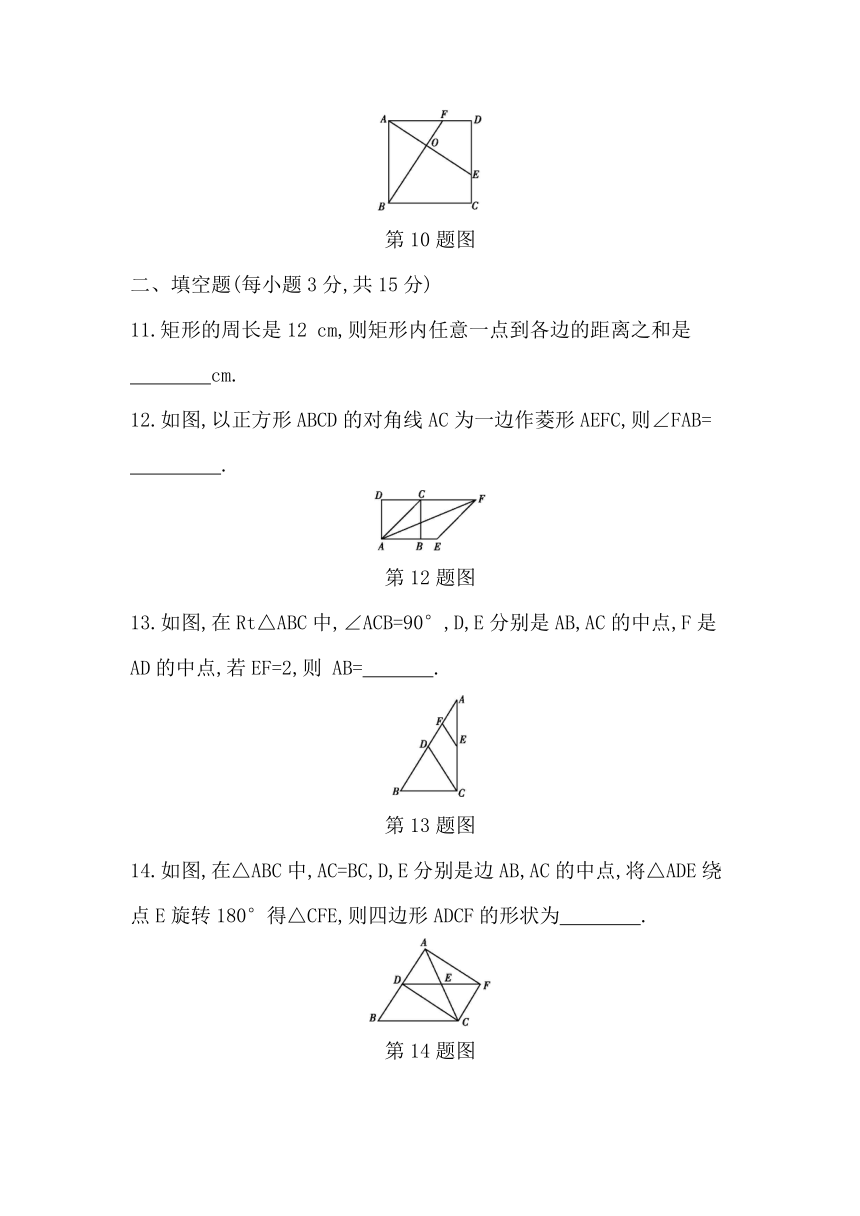
10.如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF;②AE⊥BF;③AD=OE;④S△AOB=S四边形DEOF.其中正确的有( )
(A)4个 (B)3个 (C)2个 (D)1个
第10题图
二、填空题(每小题3分,共15分)
11.矩形的周长是12 cm,则矩形内任意一点到各边的距离之和是
cm.
12.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=
.
第12题图
13.如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,F是AD的中点,若EF=2,则 AB= .
第13题图
14.如图,在△ABC中,AC=BC,D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF的形状为 .
第14题图
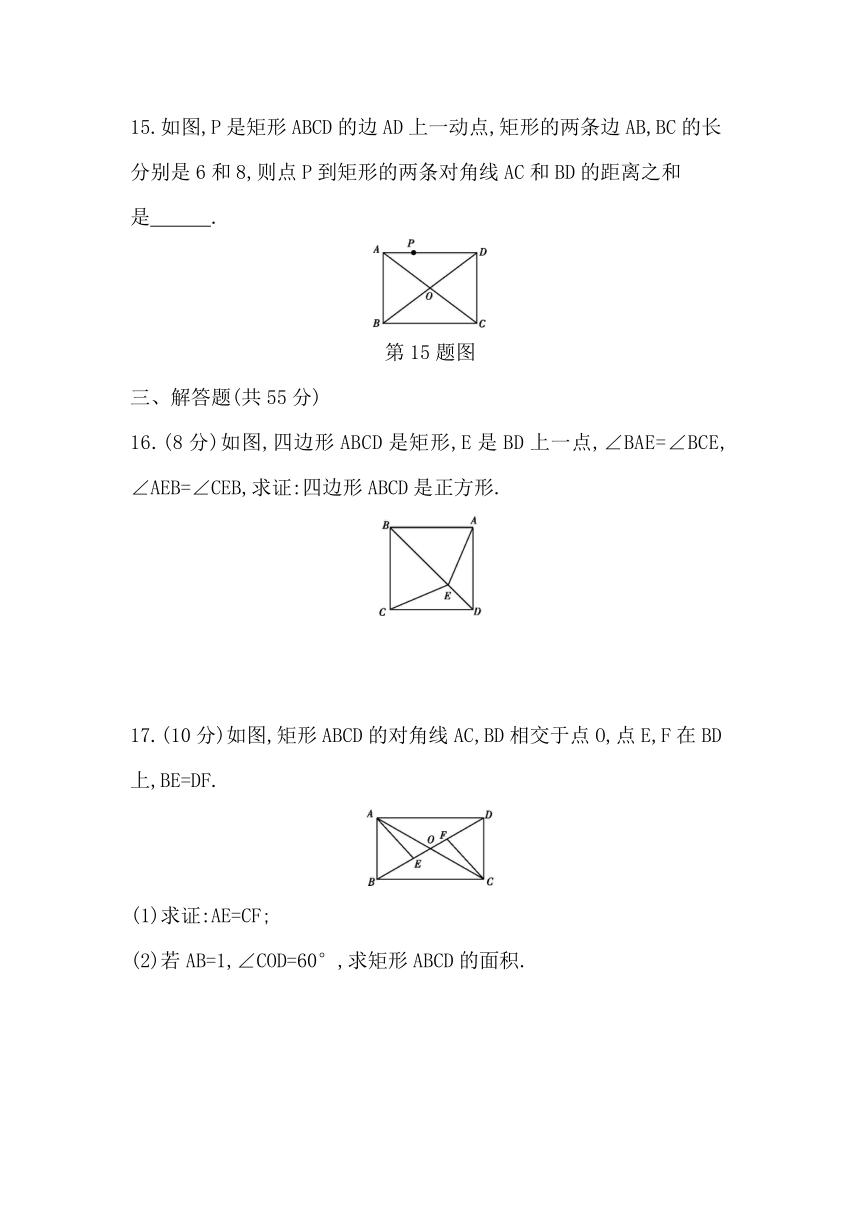
15.如图,P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 .
第15题图
三、解答题(共55分)
16.(8分)如图,四边形ABCD是矩形,E是BD上一点,∠BAE=∠BCE,
∠AEB=∠CEB,求证:四边形ABCD是正方形.
17.(10分)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=1,∠COD=60°,求矩形ABCD的面积.
18.(12分)如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
19.(12分)如图所示,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,交CD于点F,交BC于点E,过点E作EG⊥AB,点G是垂足,连接FG,求证:四边形CEGF是菱形.
20.(13分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
附加题(15分)
21.如图1,在正方形ABCD中,P是BD上一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
单元试卷 第六章
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列命题是真命题的是( C )
(A)对角线相等的四边形是矩形
(B)对角线互相垂直的四边形是矩形
(C)对角线互相垂直的矩形是正方形
(D)四边相等的平行四边形是正方形
2.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( D )
第2题图
(A)∠ABC=90° (B)AC=BD (C)OA=OB (D)OA=AD
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( B )
第3题图
(A)AB=BC (B)AC=BC (C)∠B=60° (D)∠ACB=60°
4.如图,菱形ABCD的对角线AC与BD交于点O,E是DC边的中点,连接OE,若OE=5,BD=12,则菱形的面积为( A )
第4题图
(A)96 (B)48 (C)192 (D)24
5.一个矩形的三个顶点在平面直角坐标系中的坐标分别为(-1,-2),
(3,-2),(3,1),则第四个顶点的坐标为( A )
(A)(-1,1) (B)(1,-1) (C)(-1,2) (D)(1,1)
6.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( D )
(A)DA=DE (B)∠ABC=2∠E (C)∠EAC=90° (D)BD=CE
第6题图
7.如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连接DM,DN,MN.若AB=6,则DN的长为( C )
第7题图
(A)1 (B)2 (C)3 (D)4
8.如图1为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队,如果将每位队员看成一个点,队形可近似看成由图2所示的若干个正方形拼成的图形,其中与△ABC全等的三角形是( C )
第8题图
(A)△AEG (B)△ADF (C)△DFG (D)△CEG
9.如图,E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.正确的个数是( A )
第9题图
(A)1 (B)2 (C)3 (D)4
10.如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF;②AE⊥BF;③AD=OE;④S△AOB=S四边形DEOF.其中正确的有( B )
(A)4个 (B)3个 (C)2个 (D)1个
第10题图
二、填空题(每小题3分,共15分)
11.矩形的周长是12 cm,则矩形内任意一点到各边的距离之和是
6 cm.
12.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=
22.5° .
第12题图
13.如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,F是AD的中点,若EF=2,则 AB= 8 .
第13题图
14.如图,在△ABC中,AC=BC,D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF的形状为 矩形 .
第14题图
15.如图,P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 4.8 .
第15题图
三、解答题(共55分)
16.(8分)如图,四边形ABCD是矩形,E是BD上一点,∠BAE=∠BCE,
∠AEB=∠CEB,求证:四边形ABCD是正方形.
证明:因为∠BAE=∠BCE,∠AEB=∠CEB,BE=BE,
所以△ABE≌△CBE.
所以BA=BC,
又因为四边形ABCD是矩形,
所以四边形ABCD是正方形.
17.(10分)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=1,∠COD=60°,求矩形ABCD的面积.
(1)证明:因为四边形ABCD是矩形,
所以OA=OC,OB=OD,AC=BD,∠ABC=90°.
因为BE=DF,
所以OB-BE=OD-DF,
即OE=OF.
所以△AOE≌△COF.
所以AE=CF.
(2)解:因为OA=OC,OB=OD,AC=BD,
所以OA=OB,
因为∠AOB=∠COD=60°,
所以△AOB是等边三角形.
所以OA=AB=1.
所以AC=2OA=2.
在Rt△ABC中,BC==,
所以矩形ABCD的面积S=AB·BC=1×=.
18.(12分)如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
(1)证明:因为四边形ABCD是平行四边形,
所以CF∥ED,
所以∠FCG=∠EDG.
因为G是CD的中点,
所以CG=DG.
又因为∠CGF=∠DGE,
所以△FCG≌△EDG,
所以FG=EG.
又因为CG=DG,
所以四边形CEDF是平行四边形.
(2)解:①3.5;②2.
19.(12分)如图所示,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,交CD于点F,交BC于点E,过点E作EG⊥AB,点G是垂足,连接FG,求证:四边形CEGF是菱形.
证明:因为AE平分∠BAC,∠ACB=90°,EG⊥AB,
所以EC=EG,∠BAE=∠CAE,∠ACE=∠AGE=90°,
所以∠AEC=∠AEG,
又因为EF=EF,
所以△CEF≌△GEF,
所以FC=FG,∠CFE=∠GFE,
因为CD⊥AB,EG⊥AB,
所以CD∥EG,
所以∠CFE=∠GEF,
所以∠GFE=∠GEF,
所以GE=GF,
又因为FC=FG,EC=EG,
所以CF=CE=EG=FG,
所以四边形CEGF是菱形.
20.(13分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
(1)证明:因为AF∥BC,
所以∠AFE=∠DBE,
因为E是AD的中点,
所以AE=DE.
又因为∠FEA=∠BED,
所以△AFE≌△DBE.
所以AF=BD.
因为AD是BC边上的中线,
所以DC=BD,所以AF=DC.
(2)解:四边形ADCF是菱形.证明如下:
由(1)得AF=DC,
又因为AF∥BC,
所以四边形ADCF是平行四边形,
因为AC⊥AB,AD是斜边BC的中线,
所以AD=BC=DC,
所以 ADCF是菱形.
附加题(15分)
21.如图1,在正方形ABCD中,P是BD上一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
(1)证明:因为四边形ABCD是正方形,
所以AD=CD,∠ADP=∠CDP,
又因为DP=DP,
所以△ADP≌△CDP.
所以PA=PC.
因为PA=PE,所以PC=PE.
(2)解:因为△ADP≌△CDP,
所以∠DAP=∠DCP.
因为PA=PE,所以∠DAP=∠E,
所以∠FCP=∠E.
因为∠PFC=∠DFE,∠EDF=90°,
所以∠CPE=∠EDF=90°.
(3)解:AP=CE.理由如下:
因为四边形ABCD是菱形,∠ABC=120°,
所以∠ADC=120°.
所以∠EDC=60°.
由(1),(2)同理,得∠CPE=∠EDF=60°,PC=PE,
所以△PCE是等边三角形,PE=CE,
因为PA=PE,
所以AP=CE.
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列命题是真命题的是( )
(A)对角线相等的四边形是矩形
(B)对角线互相垂直的四边形是矩形
(C)对角线互相垂直的矩形是正方形
(D)四边相等的平行四边形是正方形
2.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
第2题图
(A)∠ABC=90° (B)AC=BD (C)OA=OB (D)OA=AD
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( )
第3题图
(A)AB=BC (B)AC=BC (C)∠B=60° (D)∠ACB=60°
4.如图,菱形ABCD的对角线AC与BD交于点O,E是DC边的中点,连接OE,若OE=5,BD=12,则菱形的面积为( )
第4题图
(A)96 (B)48 (C)192 (D)24
5.一个矩形的三个顶点在平面直角坐标系中的坐标分别为(-1,-2),
(3,-2),(3,1),则第四个顶点的坐标为( )
(A)(-1,1) (B)(1,-1) (C)(-1,2) (D)(1,1)
6.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( )
(A)DA=DE (B)∠ABC=2∠E (C)∠EAC=90° (D)BD=CE
第6题图
7.如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连接DM,DN,MN.若AB=6,则DN的长为( )
第7题图
(A)1 (B)2 (C)3 (D)4
8.如图1为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队,如果将每位队员看成一个点,队形可近似看成由图2所示的若干个正方形拼成的图形,其中与△ABC全等的三角形是( )
第8题图
(A)△AEG (B)△ADF (C)△DFG (D)△CEG
9.如图,E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.正确的个数是( )
第9题图
(A)1 (B)2 (C)3 (D)4
10.如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF;②AE⊥BF;③AD=OE;④S△AOB=S四边形DEOF.其中正确的有( )
(A)4个 (B)3个 (C)2个 (D)1个
第10题图
二、填空题(每小题3分,共15分)
11.矩形的周长是12 cm,则矩形内任意一点到各边的距离之和是
cm.
12.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=
.
第12题图
13.如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,F是AD的中点,若EF=2,则 AB= .
第13题图
14.如图,在△ABC中,AC=BC,D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF的形状为 .
第14题图
15.如图,P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 .
第15题图
三、解答题(共55分)
16.(8分)如图,四边形ABCD是矩形,E是BD上一点,∠BAE=∠BCE,
∠AEB=∠CEB,求证:四边形ABCD是正方形.
17.(10分)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=1,∠COD=60°,求矩形ABCD的面积.
18.(12分)如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
19.(12分)如图所示,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,交CD于点F,交BC于点E,过点E作EG⊥AB,点G是垂足,连接FG,求证:四边形CEGF是菱形.
20.(13分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
附加题(15分)
21.如图1,在正方形ABCD中,P是BD上一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
单元试卷 第六章
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列命题是真命题的是( C )
(A)对角线相等的四边形是矩形
(B)对角线互相垂直的四边形是矩形
(C)对角线互相垂直的矩形是正方形
(D)四边相等的平行四边形是正方形
2.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( D )
第2题图
(A)∠ABC=90° (B)AC=BD (C)OA=OB (D)OA=AD
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( B )
第3题图
(A)AB=BC (B)AC=BC (C)∠B=60° (D)∠ACB=60°
4.如图,菱形ABCD的对角线AC与BD交于点O,E是DC边的中点,连接OE,若OE=5,BD=12,则菱形的面积为( A )
第4题图
(A)96 (B)48 (C)192 (D)24
5.一个矩形的三个顶点在平面直角坐标系中的坐标分别为(-1,-2),
(3,-2),(3,1),则第四个顶点的坐标为( A )
(A)(-1,1) (B)(1,-1) (C)(-1,2) (D)(1,1)
6.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( D )
(A)DA=DE (B)∠ABC=2∠E (C)∠EAC=90° (D)BD=CE
第6题图
7.如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连接DM,DN,MN.若AB=6,则DN的长为( C )
第7题图
(A)1 (B)2 (C)3 (D)4
8.如图1为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队,如果将每位队员看成一个点,队形可近似看成由图2所示的若干个正方形拼成的图形,其中与△ABC全等的三角形是( C )
第8题图
(A)△AEG (B)△ADF (C)△DFG (D)△CEG
9.如图,E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.正确的个数是( A )
第9题图
(A)1 (B)2 (C)3 (D)4
10.如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF;②AE⊥BF;③AD=OE;④S△AOB=S四边形DEOF.其中正确的有( B )
(A)4个 (B)3个 (C)2个 (D)1个
第10题图
二、填空题(每小题3分,共15分)
11.矩形的周长是12 cm,则矩形内任意一点到各边的距离之和是
6 cm.
12.如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=
22.5° .
第12题图
13.如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,F是AD的中点,若EF=2,则 AB= 8 .
第13题图
14.如图,在△ABC中,AC=BC,D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF的形状为 矩形 .
第14题图
15.如图,P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是 4.8 .
第15题图
三、解答题(共55分)
16.(8分)如图,四边形ABCD是矩形,E是BD上一点,∠BAE=∠BCE,
∠AEB=∠CEB,求证:四边形ABCD是正方形.
证明:因为∠BAE=∠BCE,∠AEB=∠CEB,BE=BE,
所以△ABE≌△CBE.
所以BA=BC,
又因为四边形ABCD是矩形,
所以四边形ABCD是正方形.
17.(10分)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=1,∠COD=60°,求矩形ABCD的面积.
(1)证明:因为四边形ABCD是矩形,
所以OA=OC,OB=OD,AC=BD,∠ABC=90°.
因为BE=DF,
所以OB-BE=OD-DF,
即OE=OF.
所以△AOE≌△COF.
所以AE=CF.
(2)解:因为OA=OC,OB=OD,AC=BD,
所以OA=OB,
因为∠AOB=∠COD=60°,
所以△AOB是等边三角形.
所以OA=AB=1.
所以AC=2OA=2.
在Rt△ABC中,BC==,
所以矩形ABCD的面积S=AB·BC=1×=.
18.(12分)如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
(1)证明:因为四边形ABCD是平行四边形,
所以CF∥ED,
所以∠FCG=∠EDG.
因为G是CD的中点,
所以CG=DG.
又因为∠CGF=∠DGE,
所以△FCG≌△EDG,
所以FG=EG.
又因为CG=DG,
所以四边形CEDF是平行四边形.
(2)解:①3.5;②2.
19.(12分)如图所示,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,交CD于点F,交BC于点E,过点E作EG⊥AB,点G是垂足,连接FG,求证:四边形CEGF是菱形.
证明:因为AE平分∠BAC,∠ACB=90°,EG⊥AB,
所以EC=EG,∠BAE=∠CAE,∠ACE=∠AGE=90°,
所以∠AEC=∠AEG,
又因为EF=EF,
所以△CEF≌△GEF,
所以FC=FG,∠CFE=∠GFE,
因为CD⊥AB,EG⊥AB,
所以CD∥EG,
所以∠CFE=∠GEF,
所以∠GFE=∠GEF,
所以GE=GF,
又因为FC=FG,EC=EG,
所以CF=CE=EG=FG,
所以四边形CEGF是菱形.
20.(13分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
(1)证明:因为AF∥BC,
所以∠AFE=∠DBE,
因为E是AD的中点,
所以AE=DE.
又因为∠FEA=∠BED,
所以△AFE≌△DBE.
所以AF=BD.
因为AD是BC边上的中线,
所以DC=BD,所以AF=DC.
(2)解:四边形ADCF是菱形.证明如下:
由(1)得AF=DC,
又因为AF∥BC,
所以四边形ADCF是平行四边形,
因为AC⊥AB,AD是斜边BC的中线,
所以AD=BC=DC,
所以 ADCF是菱形.
附加题(15分)
21.如图1,在正方形ABCD中,P是BD上一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
(1)证明:因为四边形ABCD是正方形,
所以AD=CD,∠ADP=∠CDP,
又因为DP=DP,
所以△ADP≌△CDP.
所以PA=PC.
因为PA=PE,所以PC=PE.
(2)解:因为△ADP≌△CDP,
所以∠DAP=∠DCP.
因为PA=PE,所以∠DAP=∠E,
所以∠FCP=∠E.
因为∠PFC=∠DFE,∠EDF=90°,
所以∠CPE=∠EDF=90°.
(3)解:AP=CE.理由如下:
因为四边形ABCD是菱形,∠ABC=120°,
所以∠ADC=120°.
所以∠EDC=60°.
由(1),(2)同理,得∠CPE=∠EDF=60°,PC=PE,
所以△PCE是等边三角形,PE=CE,
因为PA=PE,
所以AP=CE.
