立足化归思想玩转角的变换 (新) 高一课件(44页)
文档属性
| 名称 | 立足化归思想玩转角的变换 (新) 高一课件(44页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览










文档简介
(共44张PPT)
第一篇:前言自述
第二篇:知识理论
第三篇:实战演练
第一篇:前言自述
4个方面
努力提升自己的数学核心素养:
(1)数学抽象
(2)逻辑推理
(3)数学建模
(4)数学运算
(5)直观想象
(6)数据分析
(一)
方 整 特 数 或 化 分
中学数学思想七种思想
方程函数不等式的思想
整体的思想
特殊与一般的思想
数形结合思想
或然与必然的思想
化归与转化的思想
分类讨论与综合的思想
(二)
我 的 教 学 理 念
①强根基
②固本源
③抓重点
④破疑难
⑤研经典
⑥明考向
强基
固本
抓重
破疑
研经
明向
(三)
强化基础夯实三基
探求巩固知识的由来
紧抓教学重点
破解教学难点
研究经典例题真题
明确考纲考向
我的教学风格
(1)善于归纳总结与模型教学;
(2)擅长培养激发学生学习兴趣;
(3)注重数学思想方法的传授与渗透;
(4)能深入浅出,通俗易懂,把复杂的问
题简单化,简单的问题明了化。
(四)
第二篇:知识理论
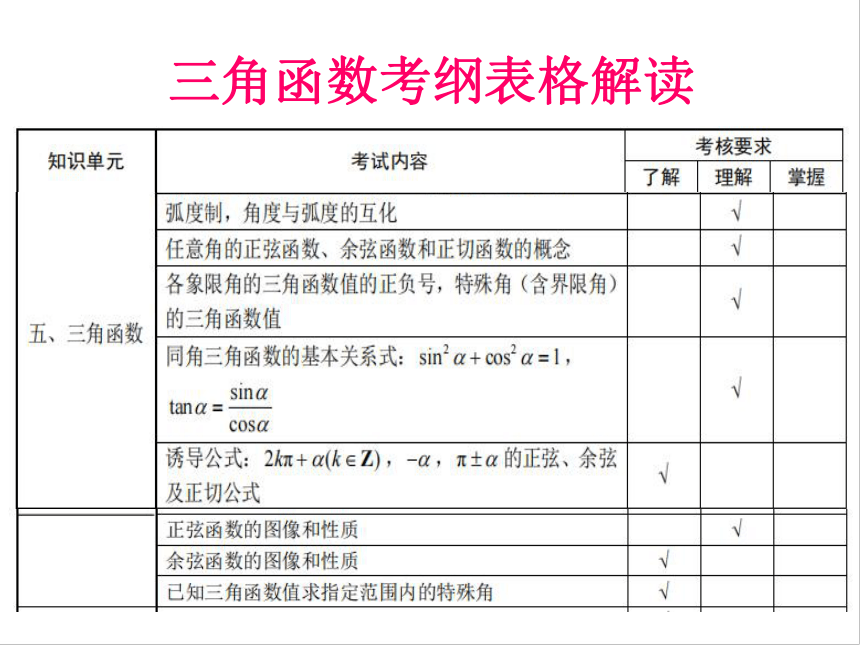
三角函数考纲表格解读
一条射线由原来的位置OA,绕着它的端点O,按逆时针(或
顺时针)方向旋转到另一位置OB 就形成角α.
旋转开始位置的射线OA叫角α的始边,终止位置的射线OB
叫做角α的终边,端点O 叫做角α的顶点.
按逆时针方向旋转所形成的角叫做正角;
按顺时针方向旋转所形成的角叫做负角;
当射线没有作任何旋转时,所形成的角叫做零角.
前提:在平面直角坐标系中,以坐标原点为顶点,
以x轴的非负半轴为始边------(本初子午线)
{β|β=k·360°+α,k∈Z}
两角的终边重合
第几象限
Ⅰ象限:{α|k·360°<α+90°,k∈Z}
Ⅱ象限:{α|k·360°+90°
<αⅣ象限:{α|k·360°
-90°<αⅢ象限:{α|k·360°
+180°<α(7个方面)
{α|α=k·360°,k∈Z}
{α|α=k·180°,k∈Z}
{α|α=k·360°+90°,k∈Z}
{α|α=k·360°+270°,k∈Z}
{α|α=k·180°+90°,k∈Z}
{α|α=k·90°,k∈Z}
{α|α=k·360°+180°,k∈Z}
(6)线性角的集合表示:
弧长等于半径的圆弧所对的
圆心角叫1弧度的角
把圆周分成360份,每一份所对的
圆心角叫1°的角
|α|·r
sinα cosα tanα
Ⅰ ____ ____ ____
Ⅱ ____ ____ ____
Ⅲ ____ ____ ____
Ⅳ ____ ____ ____
+
+
+
+
+
+
-
-
-
-
-
-
函
弦
切
余
一全正
二正弦
四余弦
三正切
sin2α+cos2α=1
(7个方面)
Sin cos tan
2kπ+α
-α
π+α
π-α
sinα
tanα
cosα
cosα
-sinα
-sinα
-tanα
-cosα
tanα
sinα
-cosα
-tanα
cosα
cosα
-sinα
sinα
解释:指 ,若K为奇数,
则函数名要改变,若K为偶数函数名不变。
记忆口诀: 奇 变 偶 不 变 ,符 号 看 象 限
用 途口诀:负化正大化小, 化成锐角特殊角
函
弦
切
余
一全正
二正弦
四余弦
三正切
2kπ+α
α
π-α
π+α
-α
2kπ-α
偶倍兀来直接去,
奇倍兀来负来续,
tan兀倍都可去,
只有负角负来续,
Sin为奇C0S偶,
tan增到天上瞅。
5.诱导公式与推广式记忆口诀
6.公式逆用妙化角
小贴士:所加的 或 要恰到好处,原则是能实现负角化正角,绝对值较大的角化为绝对值较小的角,或化成符合现有的诱导公式的形式,最终化成锐角特殊角。
7
函数 y=sinx y=cosx y=tanx
周期性
奇偶性
单调 增区间
区间 减区间
T=2π
T=2π
T=π
奇函数
偶函数
奇函数
化简求值在三角, 从角观察定导向;
函弦切余符号判, 同角关系加诱导;
恒等变换有奥妙, 两种思考细掂量;
角变换与式变换 , 结构特征最关键;
1 的代换有意做, 角隐条件细酌量。
三角函数角模型口诀
本章在高考中的地位、分值及比重的分析报告:
(一)地位:必考题、常考题、中档题、易错题。
(二)往年分值及比重:
⑴2018年: 17分 比重:18.8%
⑵2019年: 42分 比重:46.6%
⑶2020年: 18分 比重:20%
⑷2021年: 17分 比重:18.8%
(三)2022年预测:24分 比重:26.6%
第三篇:实战演练
典型例题讲解
例1、已知 ,且 α 是第三象限
的角,求 的值。
法一
例1、已知 ,且 α 是第三象限
的角,求 的值。
典型例题讲解
法二
例1、已知 ,且 α 是第三象限
的角,求 的值。
典型例题讲解
法二
解原式=
=
=
=
=
= -
例2、计算
的值.
法一
例2、计算
的值.
法二
例2、计算
的值.
法二
解:原式= -
= -
= -
= -
=
例3、计算 的值.
解:原式
法一
例3、计算 的值.
法二
例3、计算 的值.
法二
解:原式 =sin(480-360)+tan (540-180)
-
= sin120+tan0-
= + 0 -
=
例4、已知 ,且α为第二象限的角,求
的值 .
法一
例4、已知 ,且α为第二象限的角,求
的值 .
法二
例4、已知 ,且α为第二象限的角,求
的值 .
法二
解: sina= 令y=4,r=5,则x=3(都取绝对值)
又
原式=
=
=
=
=-1
点 拨 提 升
综合运用三角函数诱导公式与同角三角函数基本关系式、熟记三角函数符号口诀与特殊角对应特殊三角函数值、巧用化角公式;注重定义的思想方法在解题中的运用。
学 法 指 导
以理解为前提, 以口诀为依托,以典例为载体,让理论和实践相结合,使学生达到公式熟记、熟用、逆用、巧用、灵活运用;并注重数学思维的培养,能够善于从数学的角度去思考问题;还在生活中进行运用,把数学和我们的生活结合到一起,让学生感受到更多数学的乐趣;同时加强运算能力的培养,从而整体提升学生的数学素养。
谢谢大家!
第一篇:前言自述
第二篇:知识理论
第三篇:实战演练
第一篇:前言自述
4个方面
努力提升自己的数学核心素养:
(1)数学抽象
(2)逻辑推理
(3)数学建模
(4)数学运算
(5)直观想象
(6)数据分析
(一)
方 整 特 数 或 化 分
中学数学思想七种思想
方程函数不等式的思想
整体的思想
特殊与一般的思想
数形结合思想
或然与必然的思想
化归与转化的思想
分类讨论与综合的思想
(二)
我 的 教 学 理 念
①强根基
②固本源
③抓重点
④破疑难
⑤研经典
⑥明考向
强基
固本
抓重
破疑
研经
明向
(三)
强化基础夯实三基
探求巩固知识的由来
紧抓教学重点
破解教学难点
研究经典例题真题
明确考纲考向
我的教学风格
(1)善于归纳总结与模型教学;
(2)擅长培养激发学生学习兴趣;
(3)注重数学思想方法的传授与渗透;
(4)能深入浅出,通俗易懂,把复杂的问
题简单化,简单的问题明了化。
(四)
第二篇:知识理论
三角函数考纲表格解读
一条射线由原来的位置OA,绕着它的端点O,按逆时针(或
顺时针)方向旋转到另一位置OB 就形成角α.
旋转开始位置的射线OA叫角α的始边,终止位置的射线OB
叫做角α的终边,端点O 叫做角α的顶点.
按逆时针方向旋转所形成的角叫做正角;
按顺时针方向旋转所形成的角叫做负角;
当射线没有作任何旋转时,所形成的角叫做零角.
前提:在平面直角坐标系中,以坐标原点为顶点,
以x轴的非负半轴为始边------(本初子午线)
{β|β=k·360°+α,k∈Z}
两角的终边重合
第几象限
Ⅰ象限:{α|k·360°<α
Ⅱ象限:{α|k·360°+90°
<α
-90°<α
+180°<α
{α|α=k·360°,k∈Z}
{α|α=k·180°,k∈Z}
{α|α=k·360°+90°,k∈Z}
{α|α=k·360°+270°,k∈Z}
{α|α=k·180°+90°,k∈Z}
{α|α=k·90°,k∈Z}
{α|α=k·360°+180°,k∈Z}
(6)线性角的集合表示:
弧长等于半径的圆弧所对的
圆心角叫1弧度的角
把圆周分成360份,每一份所对的
圆心角叫1°的角
|α|·r
sinα cosα tanα
Ⅰ ____ ____ ____
Ⅱ ____ ____ ____
Ⅲ ____ ____ ____
Ⅳ ____ ____ ____
+
+
+
+
+
+
-
-
-
-
-
-
函
弦
切
余
一全正
二正弦
四余弦
三正切
sin2α+cos2α=1
(7个方面)
Sin cos tan
2kπ+α
-α
π+α
π-α
sinα
tanα
cosα
cosα
-sinα
-sinα
-tanα
-cosα
tanα
sinα
-cosα
-tanα
cosα
cosα
-sinα
sinα
解释:指 ,若K为奇数,
则函数名要改变,若K为偶数函数名不变。
记忆口诀: 奇 变 偶 不 变 ,符 号 看 象 限
用 途口诀:负化正大化小, 化成锐角特殊角
函
弦
切
余
一全正
二正弦
四余弦
三正切
2kπ+α
α
π-α
π+α
-α
2kπ-α
偶倍兀来直接去,
奇倍兀来负来续,
tan兀倍都可去,
只有负角负来续,
Sin为奇C0S偶,
tan增到天上瞅。
5.诱导公式与推广式记忆口诀
6.公式逆用妙化角
小贴士:所加的 或 要恰到好处,原则是能实现负角化正角,绝对值较大的角化为绝对值较小的角,或化成符合现有的诱导公式的形式,最终化成锐角特殊角。
7
函数 y=sinx y=cosx y=tanx
周期性
奇偶性
单调 增区间
区间 减区间
T=2π
T=2π
T=π
奇函数
偶函数
奇函数
化简求值在三角, 从角观察定导向;
函弦切余符号判, 同角关系加诱导;
恒等变换有奥妙, 两种思考细掂量;
角变换与式变换 , 结构特征最关键;
1 的代换有意做, 角隐条件细酌量。
三角函数角模型口诀
本章在高考中的地位、分值及比重的分析报告:
(一)地位:必考题、常考题、中档题、易错题。
(二)往年分值及比重:
⑴2018年: 17分 比重:18.8%
⑵2019年: 42分 比重:46.6%
⑶2020年: 18分 比重:20%
⑷2021年: 17分 比重:18.8%
(三)2022年预测:24分 比重:26.6%
第三篇:实战演练
典型例题讲解
例1、已知 ,且 α 是第三象限
的角,求 的值。
法一
例1、已知 ,且 α 是第三象限
的角,求 的值。
典型例题讲解
法二
例1、已知 ,且 α 是第三象限
的角,求 的值。
典型例题讲解
法二
解原式=
=
=
=
=
= -
例2、计算
的值.
法一
例2、计算
的值.
法二
例2、计算
的值.
法二
解:原式= -
= -
= -
= -
=
例3、计算 的值.
解:原式
法一
例3、计算 的值.
法二
例3、计算 的值.
法二
解:原式 =sin(480-360)+tan (540-180)
-
= sin120+tan0-
= + 0 -
=
例4、已知 ,且α为第二象限的角,求
的值 .
法一
例4、已知 ,且α为第二象限的角,求
的值 .
法二
例4、已知 ,且α为第二象限的角,求
的值 .
法二
解: sina= 令y=4,r=5,则x=3(都取绝对值)
又
原式=
=
=
=
=-1
点 拨 提 升
综合运用三角函数诱导公式与同角三角函数基本关系式、熟记三角函数符号口诀与特殊角对应特殊三角函数值、巧用化角公式;注重定义的思想方法在解题中的运用。
学 法 指 导
以理解为前提, 以口诀为依托,以典例为载体,让理论和实践相结合,使学生达到公式熟记、熟用、逆用、巧用、灵活运用;并注重数学思维的培养,能够善于从数学的角度去思考问题;还在生活中进行运用,把数学和我们的生活结合到一起,让学生感受到更多数学的乐趣;同时加强运算能力的培养,从而整体提升学生的数学素养。
谢谢大家!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
