25.5相似三角形的性质 课件 2022—2023学年冀教版数学九年级上册
文档属性
| 名称 | 25.5相似三角形的性质 课件 2022—2023学年冀教版数学九年级上册 |

|
|
| 格式 | zip | ||
| 文件大小 | 922.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:30:14 | ||
图片预览




文档简介
(共17张PPT)
25.5 相似三角形的性质
冀教版九上
第二十五章 图形的相似
02 会利用相似三角形的性质解决问题.
01 相似三角形的性质似
学习目标
冀教版九上
新课学习
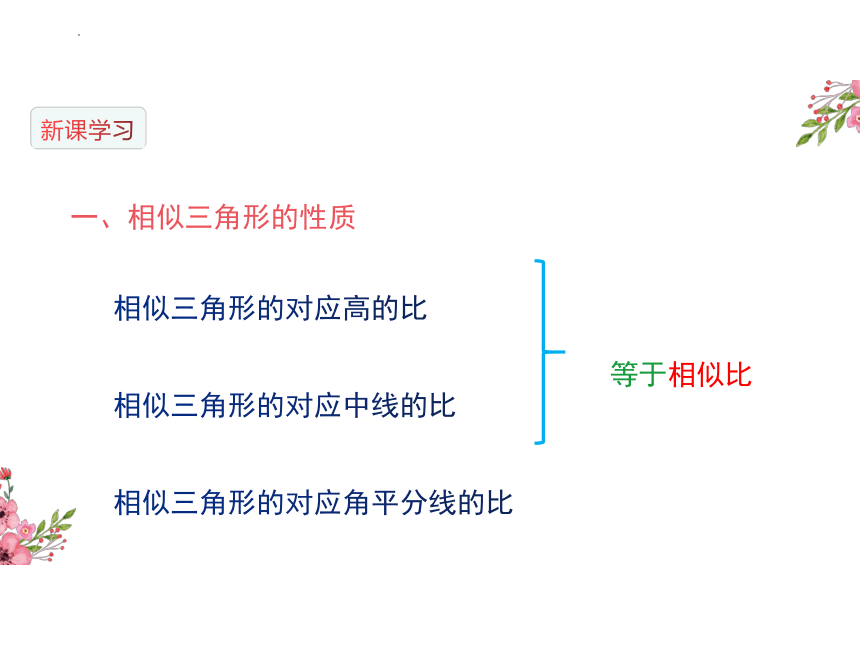
一、相似三角形的性质
相似三角形的对应高的比
相似三角形的对应中线的比
相似三角形的对应角平分线的比
等于相似比
基础小练
1.(课本85页练习)已知△ABC∽△A'B'C',相似比为2:3.
(1)若AD、A'D'分别为两个三角形的对应高,AD=9cm,则A'D'=____.
(2)若AE、A'E'分别为两个三角形的对应中线,A'E'=10cm,则A'D'=____.
(3)若AF、A'F'分别为两个三角形的对应角平分线,
你填反了吗?
基础小练
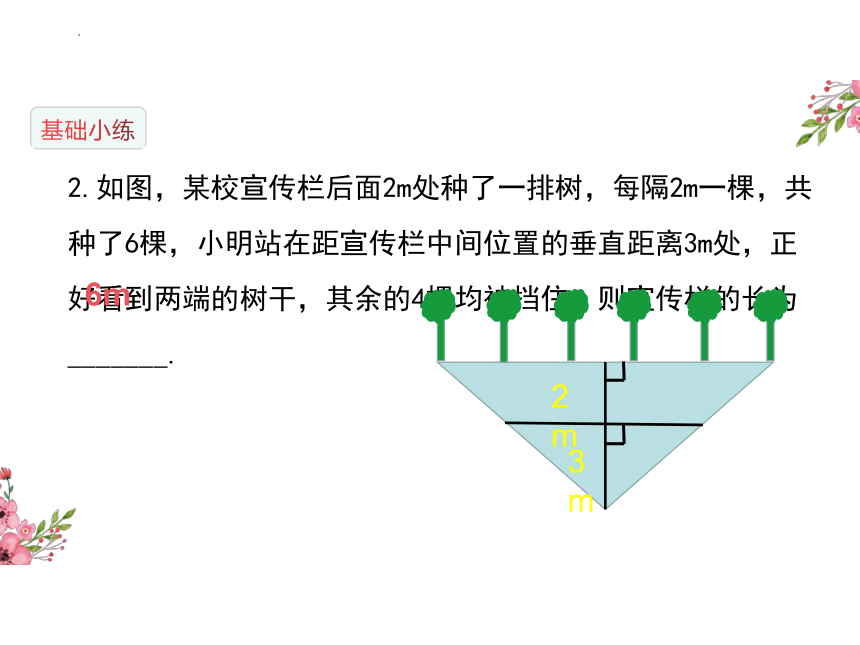
2.如图,某校宣传栏后面2m处种了一排树,每隔2m一棵,共种了6棵,小明站在距宣传栏中间位置的垂直距离3m处,正好看到两端的树干,其余的4棵均被挡住,则宣传栏的长为_______.
2m
3m
6m
典例精析
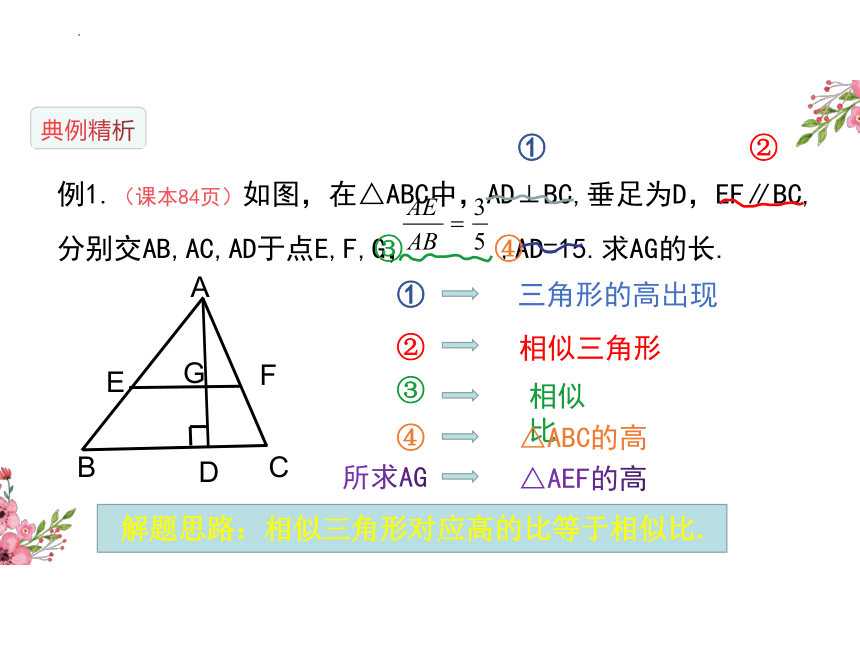
例1.(课本84页)如图,在△ABC中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD于点E,F,G, ,AD=15.求AG的长.
①
②
③
④
①
三角形的高出现
②
相似三角形
③
相似比
④
A
B
C
E
F
D
G
△ABC的高
所求AG
△AEF的高
解题思路:相似三角形对应高的比等于相似比.
典例精析
A
B
C
E
F
D
G
解:∵EF∥BC
∴△AEF∽△ABC
∴AD⊥BC
∴AG⊥EF
解得,AG=8
(相似三角形对应高的比等于相似比)
典例精析
例1.(拓展)如图,一块材料的形状是锐角△ABC,边BC=12cm,高AD=8cm,把它加工成正方形零件PQMN,要使正方形的一边在BC上,其余两个顶点分别在AB,AC上.求这个正方形零件的边长.
A
B
C
N
M
Q
P
D
分析:
1.从图形中提取与例1相同的图形
2.思路:相似三角形对应高的比等于相似比.
典例精析
A
B
C
N
M
Q
P
D
E
解:设PQ与AD交于点E
∵四边形PQMN是正方形
∴PQ∥BC
∴△APQ∽△ABC
设正方形的边长为x,则PQ=x,AE=8-x
解得,x=4.8
∴这个正方形零件的边长是4.8cm.
(相似三角形对应高的比等于相似比)
典例精析
例2.如图,在平行四边形ABCD中,AD=10,CD=6,E为AD上一点,且BE=BC,CE=CD,BM平分∠EBC,交CE于点M,CN平分∠ECD,交ED于点N.
A
D
C
B
E
N
M
△EBC∽△ECD
相似三角形对应角平分线的比等于相似比
新课学习
相似三角形的性质
2.相似三角形的面积之比等于相似比的平方
1.相似三角形的周长之比等于相似比
如:若△ABC∽△A'B'C',相似比为3:5,则周长比为____;面积比为______.
3:5
9:25
典例精析
例1.已知:如图,△ABC中,DE∥BC.AD:DB=1:2,解决下列问题.
相似比AD:AB=1:3
A
B
C
D
E
基础练习
相似比为1:3
周长比为1:3
A
B
C
D
E
6
基础练习
相似比为1:3
面积比为1:9
A
B
C
D
E
8
基础练习
高相等的两个三角形的面积之比等于底边之比
注意:△ADE与△BDE的特点是:不相似,高相等
A
B
C
D
E
回顾小结
1.对应角相等
2.对应边成比例
3.对应线段(高、中线、角平分线)的比等于相似比
相似三角形的性质
4.周长比等于相似比,面积比等于相似比的平方
同学们再见
25.5 相似三角形的性质
冀教版九上
第二十五章 图形的相似
02 会利用相似三角形的性质解决问题.
01 相似三角形的性质似
学习目标
冀教版九上
新课学习
一、相似三角形的性质
相似三角形的对应高的比
相似三角形的对应中线的比
相似三角形的对应角平分线的比
等于相似比
基础小练
1.(课本85页练习)已知△ABC∽△A'B'C',相似比为2:3.
(1)若AD、A'D'分别为两个三角形的对应高,AD=9cm,则A'D'=____.
(2)若AE、A'E'分别为两个三角形的对应中线,A'E'=10cm,则A'D'=____.
(3)若AF、A'F'分别为两个三角形的对应角平分线,
你填反了吗?
基础小练
2.如图,某校宣传栏后面2m处种了一排树,每隔2m一棵,共种了6棵,小明站在距宣传栏中间位置的垂直距离3m处,正好看到两端的树干,其余的4棵均被挡住,则宣传栏的长为_______.
2m
3m
6m
典例精析
例1.(课本84页)如图,在△ABC中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD于点E,F,G, ,AD=15.求AG的长.
①
②
③
④
①
三角形的高出现
②
相似三角形
③
相似比
④
A
B
C
E
F
D
G
△ABC的高
所求AG
△AEF的高
解题思路:相似三角形对应高的比等于相似比.
典例精析
A
B
C
E
F
D
G
解:∵EF∥BC
∴△AEF∽△ABC
∴AD⊥BC
∴AG⊥EF
解得,AG=8
(相似三角形对应高的比等于相似比)
典例精析
例1.(拓展)如图,一块材料的形状是锐角△ABC,边BC=12cm,高AD=8cm,把它加工成正方形零件PQMN,要使正方形的一边在BC上,其余两个顶点分别在AB,AC上.求这个正方形零件的边长.
A
B
C
N
M
Q
P
D
分析:
1.从图形中提取与例1相同的图形
2.思路:相似三角形对应高的比等于相似比.
典例精析
A
B
C
N
M
Q
P
D
E
解:设PQ与AD交于点E
∵四边形PQMN是正方形
∴PQ∥BC
∴△APQ∽△ABC
设正方形的边长为x,则PQ=x,AE=8-x
解得,x=4.8
∴这个正方形零件的边长是4.8cm.
(相似三角形对应高的比等于相似比)
典例精析
例2.如图,在平行四边形ABCD中,AD=10,CD=6,E为AD上一点,且BE=BC,CE=CD,BM平分∠EBC,交CE于点M,CN平分∠ECD,交ED于点N.
A
D
C
B
E
N
M
△EBC∽△ECD
相似三角形对应角平分线的比等于相似比
新课学习
相似三角形的性质
2.相似三角形的面积之比等于相似比的平方
1.相似三角形的周长之比等于相似比
如:若△ABC∽△A'B'C',相似比为3:5,则周长比为____;面积比为______.
3:5
9:25
典例精析
例1.已知:如图,△ABC中,DE∥BC.AD:DB=1:2,解决下列问题.
相似比AD:AB=1:3
A
B
C
D
E
基础练习
相似比为1:3
周长比为1:3
A
B
C
D
E
6
基础练习
相似比为1:3
面积比为1:9
A
B
C
D
E
8
基础练习
高相等的两个三角形的面积之比等于底边之比
注意:△ADE与△BDE的特点是:不相似,高相等
A
B
C
D
E
回顾小结
1.对应角相等
2.对应边成比例
3.对应线段(高、中线、角平分线)的比等于相似比
相似三角形的性质
4.周长比等于相似比,面积比等于相似比的平方
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
