苏科版八年级数学上册 6.1函数(第一课时)课件 2022-2023学年(共28张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 6.1函数(第一课时)课件 2022-2023学年(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 07:15:14 | ||
图片预览







文档简介
(共28张PPT)
6.1 函数(第一课时)
苏科版数学八年级上册
认识一下我们今天的小主人公
小芳是一名初二学生,学校组织第二天去动物园秋游,请同学们一起跟随小芳,开始我们今天的探索之旅......
秋游前的准备
小芳和爸爸妈妈一起来到超市,买了苹果,称重后,小芳研究了袋子上的标签。
1、在这个标签上有哪些量?
2、在这个购买过程中哪个量没有变化?哪些量发生了变化?
常量与变量
在某一变化过程中,数值保持不变的量叫做常量,可以取不同数值的量叫做变量.
秋游前的准备
小芳和爸爸妈妈一起来到超市,买了苹果,称重后,小芳研究了袋子上的标签。
重量和总价这两个变量之间存在什么样的关系呢?
当重量变化时,总价也随之变化,当重量确定时,总价也确定。
对于重量的每一个值,都有唯一的总价与它对应。
秋游前的准备
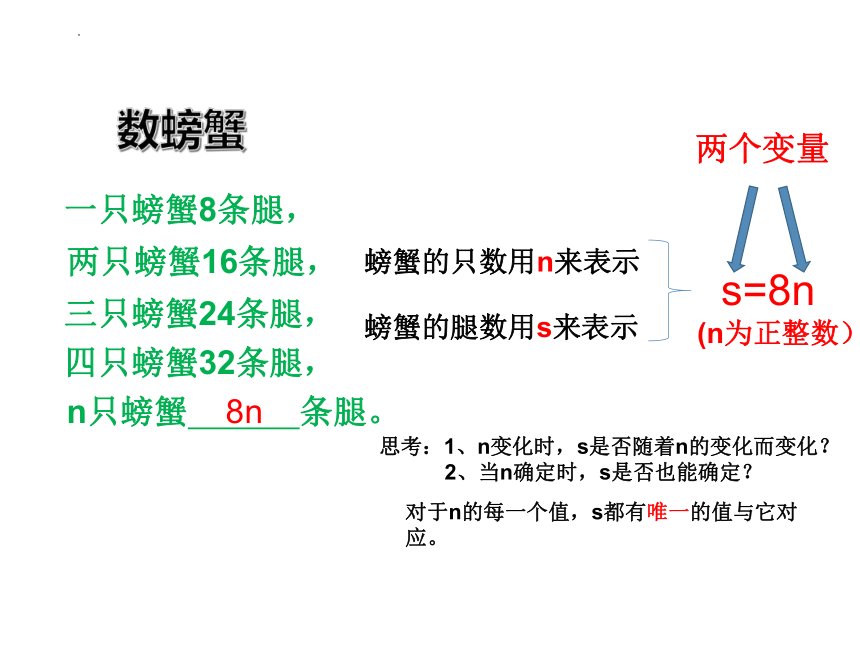
买完苹果,小芳一家人路过了生鲜区,小芳看到了玻璃柜里的螃蟹,她通过观察,发现每只螃蟹有8条腿,于是,她开始了数螃蟹...
数螃蟹
一只螃蟹8条腿,
两只螃蟹16条腿,
三只螃蟹24条腿,
n只螃蟹 条腿。
8n
螃蟹的只数用n来表示
螃蟹的腿数用s来表示
s=8n
(n为正整数)
四只螃蟹32条腿,
两个变量
思考:1、n变化时,s是否随着n的变化而变化?
2、当n确定时,s是否也能确定?
对于n的每一个值,s都有唯一的值与它对应。
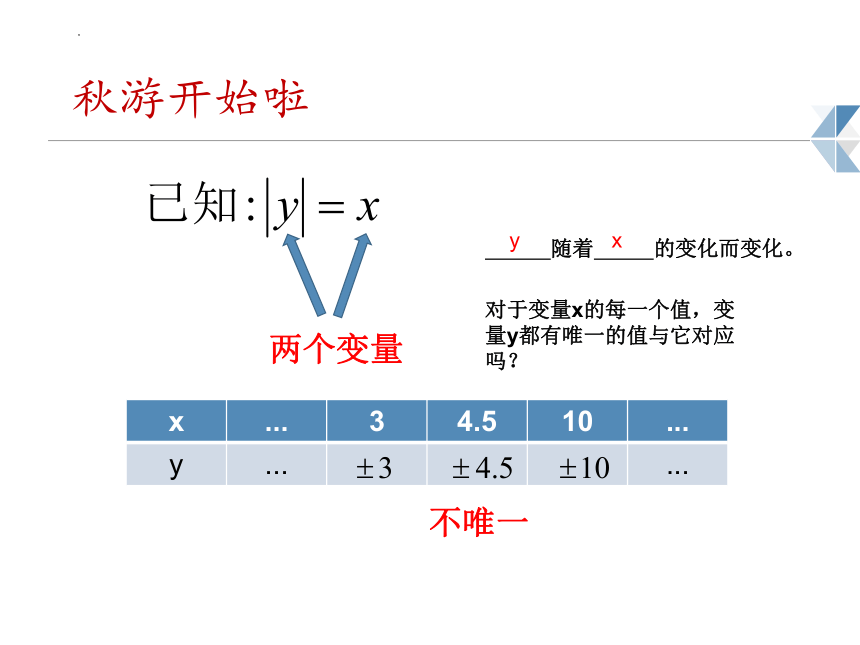
秋游开始啦
第二天,小芳和同学们一起坐上了旅游大巴,小芳的同学小丽向小芳请教了一道数学题,小丽是这样做的:
同学们,你们觉得对吗?
秋游开始啦
x ... 3 4.5 10 ...
y ... ...
两个变量
随着 的变化而变化。
对于变量x的每一个值,变量y都有唯一的值与它对应吗?
不唯一
y
x
秋游开始啦
相同点 不同点
总价与重量
s=8n
两个变量
两个变量
两个变量
对于n的每一个值,s都有唯一的值与它对应。
同学们,你们能从刚刚的几个变化过程中,找出他们的相同点与不同点吗?
对于重量的每一个值,总价都有唯一的值与它对应。
对于x的每一个值,y与它对应的值不唯一。
秋游开始啦
到了动物园,小芳来到了骆驼园,她从饲养员那里了解到骆驼的体温随时间的变化而变化,具体如图:
在这个变化过程中,有几个变量?
对于时间的每一个值,骆驼的体温有几个值与它对应?
唯一
两个
接着,小芳来到了一个水库边,她在墙面上看到了一张水库的水位变化与水库蓄水量的变化情况图:
水位/m
蓄水量/m
106
120
133
135
2.30×107
7.09×107
1.18×108
1.23×108
水位/m 106 120 133 135 ......
蓄水量/m3 2.30×107 7.09×107 1.18×108 1.23×108 ......
在这个变化过程中,有几个变量?变量之间存在怎样的关系?
同学们,你们能从刚才的几个变化过程中找到它们的共同之处吗?
2、s=8n(n为正整数)
1、总价与重量
3、
水位/m 106 120 133 135 ......
蓄水量/m3 2.30×107 7.09×107 1.18×108 1.23×108 ......
4、
上述的每个变化过程中,都有两个变量,并且其中一个变量变化时,另一个变量也随之变化,对于其中一个变量的每一个值,另一个变量有唯一的值与它对应。
举例子
你还能举出生活中或学习中的类似的变化过程吗?
函数的定义
一般地, 在一个变化过程中的两个变量 x 和 y, 如果对于x 的每一个值, y 都有唯一的值与它对应,那么我们称 y 是x 的函数,x 是自变量。
2、s=8n(n为正整数)
1、总价与重量
3、
水位/m 106 120 133 135 ......
蓄水量/m3 2.30×107 7.09×107 1.18×108 1.23×108 ......
4、
总价是重量的函数吗?
螃蟹的腿数s是螃蟹只数n的函数吗?
蓄水池的蓄水量是蓄水池水位的函数吗?
骆驼的体温是时间
的函数吗?
y是x的函数吗?
2、s=8n(n为正整数)
4、
螃蟹的腿数s是螃蟹只数n的函数吗?
骆驼的体温是时间
的函数吗?
螃蟹的只数n是螃蟹腿数s的函数吗?
时间是骆驼的体温
的函数吗?
s 8 24 40 80 ...
n ...
1
3
5
10
秋游结束啦
小芳的秋游结束啦,我们的探索与研究也接近尾声,下面请同学们利用函数的知识来解决几个问题。
学以致用:
1、用一根20m长的栅栏围成一个长方形鸡舍.
(1)当长方形的宽为2m时,长为______m;
(2)当长方形的宽为4m时,长为______m;
(3)当长方形的宽为am时,长为_______m.
这个长方形的长是宽的函数吗?为什么?
8
6
(10-a)
学以致用:
2、按图示的运算程序,输入一个实数 x,便可以输出一个相应的实数 y 。
y 是 x 的函数吗?
学以致用:
3、下列各图中,表示y是x的函数的是:( )
学以致用:
4、下列变化过程中,y是x的函数吗?
x 1 -1 3 -3.5
y
x 1 4 9 16
y
1
1
3
3.5
是
不是
学以致用:
5、根据小鱼的条数与所需火柴棒的根数的关系,填写下表。
小鱼条数(n)(n为正整数) 1 2 3 ... n
火柴根数(s)
8
14
20
...
6n+2
s=6n+2
火柴的根数s是小鱼条数n的函数。
能力提高:
6、用60cm的篱笆围成长方形,使长方形一边靠墙(墙足够长),另三边用篱笆围成。
(1)写出长方形面积s( )与垂直于墙的一边长a(m)的关系式;
(2)指出上式中的函数与自变量。
墙
归纳总结:
你能说说这节课的收获吗?
函数是中学数学中最重要的概念之一。函数概念产生于300年前。
1637年前后笛卡尔已经注意到一个变量对另一个变量的依赖关系,之后,莱布尼茨等很多数学家都在尝试给函数做出准确的定义。
中国清代数学家李善兰,在《代数学》中“function”翻译为“函数”,他解释说:“凡此变数中函彼变数者,则此为彼之函数”。此后,这个名称一直沿用至今。
笛卡尔:法国著名的哲学家、数学家、物理学家。被誉为“近代科学的始祖”
莱布尼茨:德国哲学家、数学家,历史上少见的通才,被誉为十七世纪的亚里士多德。
李善兰:中国近代著名的数学、天文学、力学和植物学家
函数的起源
结束语:
今天我们用数学的眼睛看清了一些特殊的“变化”与“联系”,用智慧的钥匙开启了“函数”的大门,从今往后,大家就可以在函数的世界里遨游了......
谢谢!
6.1 函数(第一课时)
苏科版数学八年级上册
认识一下我们今天的小主人公
小芳是一名初二学生,学校组织第二天去动物园秋游,请同学们一起跟随小芳,开始我们今天的探索之旅......
秋游前的准备
小芳和爸爸妈妈一起来到超市,买了苹果,称重后,小芳研究了袋子上的标签。
1、在这个标签上有哪些量?
2、在这个购买过程中哪个量没有变化?哪些量发生了变化?
常量与变量
在某一变化过程中,数值保持不变的量叫做常量,可以取不同数值的量叫做变量.
秋游前的准备
小芳和爸爸妈妈一起来到超市,买了苹果,称重后,小芳研究了袋子上的标签。
重量和总价这两个变量之间存在什么样的关系呢?
当重量变化时,总价也随之变化,当重量确定时,总价也确定。
对于重量的每一个值,都有唯一的总价与它对应。
秋游前的准备
买完苹果,小芳一家人路过了生鲜区,小芳看到了玻璃柜里的螃蟹,她通过观察,发现每只螃蟹有8条腿,于是,她开始了数螃蟹...
数螃蟹
一只螃蟹8条腿,
两只螃蟹16条腿,
三只螃蟹24条腿,
n只螃蟹 条腿。
8n
螃蟹的只数用n来表示
螃蟹的腿数用s来表示
s=8n
(n为正整数)
四只螃蟹32条腿,
两个变量
思考:1、n变化时,s是否随着n的变化而变化?
2、当n确定时,s是否也能确定?
对于n的每一个值,s都有唯一的值与它对应。
秋游开始啦
第二天,小芳和同学们一起坐上了旅游大巴,小芳的同学小丽向小芳请教了一道数学题,小丽是这样做的:
同学们,你们觉得对吗?
秋游开始啦
x ... 3 4.5 10 ...
y ... ...
两个变量
随着 的变化而变化。
对于变量x的每一个值,变量y都有唯一的值与它对应吗?
不唯一
y
x
秋游开始啦
相同点 不同点
总价与重量
s=8n
两个变量
两个变量
两个变量
对于n的每一个值,s都有唯一的值与它对应。
同学们,你们能从刚刚的几个变化过程中,找出他们的相同点与不同点吗?
对于重量的每一个值,总价都有唯一的值与它对应。
对于x的每一个值,y与它对应的值不唯一。
秋游开始啦
到了动物园,小芳来到了骆驼园,她从饲养员那里了解到骆驼的体温随时间的变化而变化,具体如图:
在这个变化过程中,有几个变量?
对于时间的每一个值,骆驼的体温有几个值与它对应?
唯一
两个
接着,小芳来到了一个水库边,她在墙面上看到了一张水库的水位变化与水库蓄水量的变化情况图:
水位/m
蓄水量/m
106
120
133
135
2.30×107
7.09×107
1.18×108
1.23×108
水位/m 106 120 133 135 ......
蓄水量/m3 2.30×107 7.09×107 1.18×108 1.23×108 ......
在这个变化过程中,有几个变量?变量之间存在怎样的关系?
同学们,你们能从刚才的几个变化过程中找到它们的共同之处吗?
2、s=8n(n为正整数)
1、总价与重量
3、
水位/m 106 120 133 135 ......
蓄水量/m3 2.30×107 7.09×107 1.18×108 1.23×108 ......
4、
上述的每个变化过程中,都有两个变量,并且其中一个变量变化时,另一个变量也随之变化,对于其中一个变量的每一个值,另一个变量有唯一的值与它对应。
举例子
你还能举出生活中或学习中的类似的变化过程吗?
函数的定义
一般地, 在一个变化过程中的两个变量 x 和 y, 如果对于x 的每一个值, y 都有唯一的值与它对应,那么我们称 y 是x 的函数,x 是自变量。
2、s=8n(n为正整数)
1、总价与重量
3、
水位/m 106 120 133 135 ......
蓄水量/m3 2.30×107 7.09×107 1.18×108 1.23×108 ......
4、
总价是重量的函数吗?
螃蟹的腿数s是螃蟹只数n的函数吗?
蓄水池的蓄水量是蓄水池水位的函数吗?
骆驼的体温是时间
的函数吗?
y是x的函数吗?
2、s=8n(n为正整数)
4、
螃蟹的腿数s是螃蟹只数n的函数吗?
骆驼的体温是时间
的函数吗?
螃蟹的只数n是螃蟹腿数s的函数吗?
时间是骆驼的体温
的函数吗?
s 8 24 40 80 ...
n ...
1
3
5
10
秋游结束啦
小芳的秋游结束啦,我们的探索与研究也接近尾声,下面请同学们利用函数的知识来解决几个问题。
学以致用:
1、用一根20m长的栅栏围成一个长方形鸡舍.
(1)当长方形的宽为2m时,长为______m;
(2)当长方形的宽为4m时,长为______m;
(3)当长方形的宽为am时,长为_______m.
这个长方形的长是宽的函数吗?为什么?
8
6
(10-a)
学以致用:
2、按图示的运算程序,输入一个实数 x,便可以输出一个相应的实数 y 。
y 是 x 的函数吗?
学以致用:
3、下列各图中,表示y是x的函数的是:( )
学以致用:
4、下列变化过程中,y是x的函数吗?
x 1 -1 3 -3.5
y
x 1 4 9 16
y
1
1
3
3.5
是
不是
学以致用:
5、根据小鱼的条数与所需火柴棒的根数的关系,填写下表。
小鱼条数(n)(n为正整数) 1 2 3 ... n
火柴根数(s)
8
14
20
...
6n+2
s=6n+2
火柴的根数s是小鱼条数n的函数。
能力提高:
6、用60cm的篱笆围成长方形,使长方形一边靠墙(墙足够长),另三边用篱笆围成。
(1)写出长方形面积s( )与垂直于墙的一边长a(m)的关系式;
(2)指出上式中的函数与自变量。
墙
归纳总结:
你能说说这节课的收获吗?
函数是中学数学中最重要的概念之一。函数概念产生于300年前。
1637年前后笛卡尔已经注意到一个变量对另一个变量的依赖关系,之后,莱布尼茨等很多数学家都在尝试给函数做出准确的定义。
中国清代数学家李善兰,在《代数学》中“function”翻译为“函数”,他解释说:“凡此变数中函彼变数者,则此为彼之函数”。此后,这个名称一直沿用至今。
笛卡尔:法国著名的哲学家、数学家、物理学家。被誉为“近代科学的始祖”
莱布尼茨:德国哲学家、数学家,历史上少见的通才,被誉为十七世纪的亚里士多德。
李善兰:中国近代著名的数学、天文学、力学和植物学家
函数的起源
结束语:
今天我们用数学的眼睛看清了一些特殊的“变化”与“联系”,用智慧的钥匙开启了“函数”的大门,从今往后,大家就可以在函数的世界里遨游了......
谢谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
