人教版八年级数学上册11.3.2 多边形的内角和 课件 2022-2023学年(共21张PPT)
文档属性
| 名称 | 人教版八年级数学上册11.3.2 多边形的内角和 课件 2022-2023学年(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
1
(1)从同一顶点引出的对角线的条数:
n-3
(2)多边形对角线的总条数:
(3)分割出的三角形的个数:
n-2
温故知新
11.3.2 多边形的内角和
11.3 多边形
我们知道,三角形的内角和等于180 °
那么长方形、正方形的内角和是多少呢?
长方形、正方形的内角和是360 °.
问题引入
想一想:任意四边形的内角和是多少?
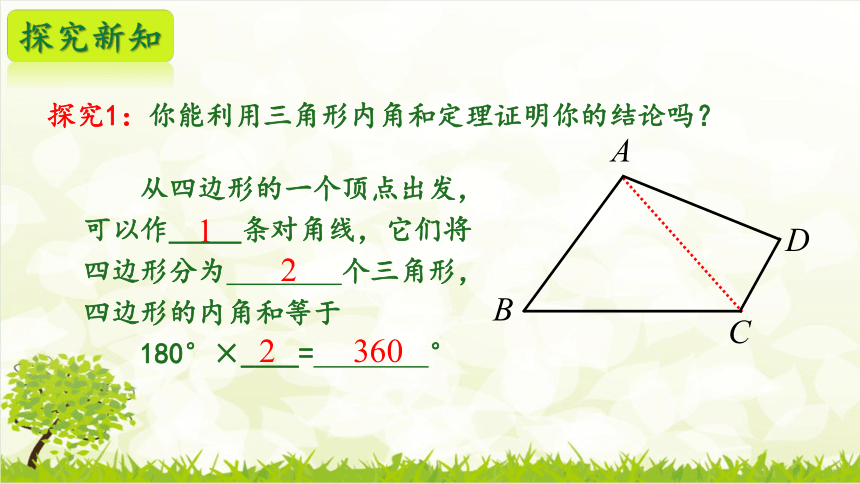
探究1:你能利用三角形内角和定理证明你的结论吗?
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °
1
2
2
360
A
B
C
D
探究新知
A
B
C
D
E
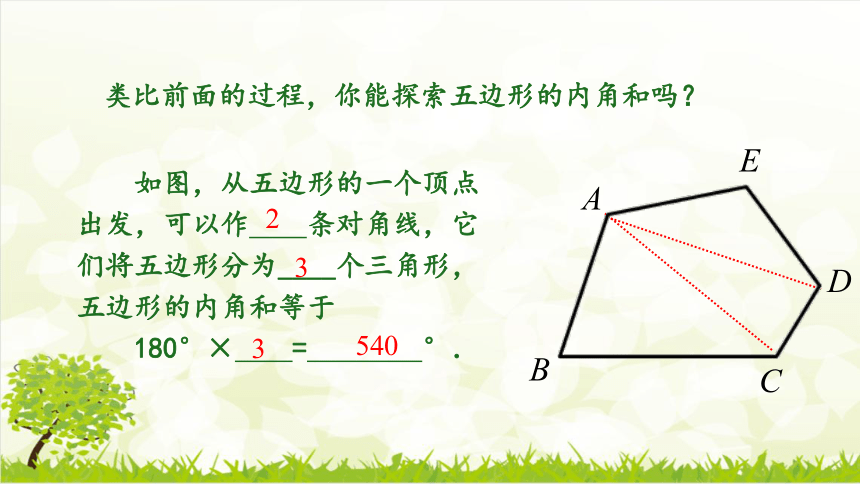
类比前面的过程,你能探索五边形的内角和吗?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
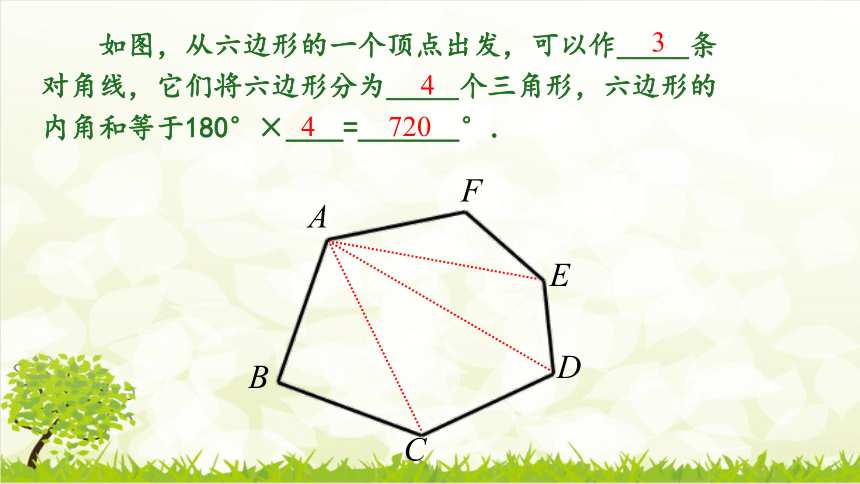
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.
3
4
4
720
C
A
B
D
E
F
这种探索方法你掌握了吗?请完成下表
多边形的边数 三 四 五 六 七 … n
分成的三角形个数 1 2 …
多边形的内角和 180° 2×180° 3×180° 4×180° …
3
4
5
n-2
(n-2) ×180
想一想:从表中你能发现什么?
5×180°
多边形的内角和公式:
n边形的内角和等于(n-2)×180°.
由特殊到一般
转化思想
探究的过程体现了什么数学方法和思想?
填空:
(1)十边形的内角和为 度.
(2)已知一个多边形的内角和为1080°,则它的边
数为______.
1440
8
小试牛刀
1.三角形的内角和是:________
2.四边形的内角和是:________
3.五边形的内角和是:________
4.六边形的内角和是:________
180°
360°
540°
720°
探究2:填空,你发现了什么规律?
多边形边数增加1,内角和增加180°
深入探究
探究3:下面正多边形的每一个内角的度数是多少呢?
180°÷3 = 60°
360°÷4 = 90°
540°÷5 = 108°
720°÷6 = 120°
正多边形的每一个内角的度数:
小结归纳
1.多边形的内角和公式:
(n-2)×180°.
2.多边形边数增加1,内角和增加180°
3.正多边形的每一个内角的度数:
一个正多边形每一个内角都是120°,这个多边形是( )
A.正四边形 B.正五边形
C.正六边形 D.正七边形
C
小试牛刀
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°= 360°,
又∵∠A+∠C = 180°,
∴∠B+∠D = 360°-(∠A+∠C)= 180°.
如果四边形一组对角互补,那么另一组对角也互补.
A
C
D
B
典例精析
如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
运用了整体思想
针对练习
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,
∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
∴△DCF为直角三角形.
你还记得如何求三角形的外角和吗?
三角形的外角之和为3600
3×180°-180°= 360°
深入探究
那么,如何求四边形的外角和呢?
四边形的外角之和为360°
4×180°-360°=360°
A
B
C
D
1
2
3
4
5
5×180°-540°=360°
五边形的外角之和为360°
思考:如果是n边形呢?
思考:如何求五边形的外角和呢?
多边形的外角和都等于360°
结论:
正多边形的每一个外角的度数是:
如图,从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向. 在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和等于一个周角,所以多边形的外角和等于360°.
多边形的外角和等于360°
结论:
1.如果一个多边形的每一个外角等于30°,则这个多边形的边数是( )
A. 8 B. 10 C. 12 D.14
学以致用
C
2.一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
C
3.正五边形的每一个外角等于____.每一个内角等于_____.
72°
108°
4.正十二边形的每个外角等于______.
30°
5.若一个正多边形的每个内角为144°,则这个正多边形的
边数为_____.
10
课堂小结
1.多边形的内角和公式:
(n-2)×180°.
2.多边形边数增加1,内角和增加180°
3.正多边形的每一个内角的度数:
5.多边形的外角和都等于360°
6.正多边形的每一个外角的度数是:
1
(1)从同一顶点引出的对角线的条数:
n-3
(2)多边形对角线的总条数:
(3)分割出的三角形的个数:
n-2
温故知新
11.3.2 多边形的内角和
11.3 多边形
我们知道,三角形的内角和等于180 °
那么长方形、正方形的内角和是多少呢?
长方形、正方形的内角和是360 °.
问题引入
想一想:任意四边形的内角和是多少?
探究1:你能利用三角形内角和定理证明你的结论吗?
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °
1
2
2
360
A
B
C
D
探究新知
A
B
C
D
E
类比前面的过程,你能探索五边形的内角和吗?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.
3
4
4
720
C
A
B
D
E
F
这种探索方法你掌握了吗?请完成下表
多边形的边数 三 四 五 六 七 … n
分成的三角形个数 1 2 …
多边形的内角和 180° 2×180° 3×180° 4×180° …
3
4
5
n-2
(n-2) ×180
想一想:从表中你能发现什么?
5×180°
多边形的内角和公式:
n边形的内角和等于(n-2)×180°.
由特殊到一般
转化思想
探究的过程体现了什么数学方法和思想?
填空:
(1)十边形的内角和为 度.
(2)已知一个多边形的内角和为1080°,则它的边
数为______.
1440
8
小试牛刀
1.三角形的内角和是:________
2.四边形的内角和是:________
3.五边形的内角和是:________
4.六边形的内角和是:________
180°
360°
540°
720°
探究2:填空,你发现了什么规律?
多边形边数增加1,内角和增加180°
深入探究
探究3:下面正多边形的每一个内角的度数是多少呢?
180°÷3 = 60°
360°÷4 = 90°
540°÷5 = 108°
720°÷6 = 120°
正多边形的每一个内角的度数:
小结归纳
1.多边形的内角和公式:
(n-2)×180°.
2.多边形边数增加1,内角和增加180°
3.正多边形的每一个内角的度数:
一个正多边形每一个内角都是120°,这个多边形是( )
A.正四边形 B.正五边形
C.正六边形 D.正七边形
C
小试牛刀
例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°= 360°,
又∵∠A+∠C = 180°,
∴∠B+∠D = 360°-(∠A+∠C)= 180°.
如果四边形一组对角互补,那么另一组对角也互补.
A
C
D
B
典例精析
如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°,
运用了整体思想
针对练习
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°,
∵BE∥DF,
∴∠EBF=∠CFD,
∴∠CDF+∠CFD=90°,
∴△DCF为直角三角形.
你还记得如何求三角形的外角和吗?
三角形的外角之和为3600
3×180°-180°= 360°
深入探究
那么,如何求四边形的外角和呢?
四边形的外角之和为360°
4×180°-360°=360°
A
B
C
D
1
2
3
4
5
5×180°-540°=360°
五边形的外角之和为360°
思考:如果是n边形呢?
思考:如何求五边形的外角和呢?
多边形的外角和都等于360°
结论:
正多边形的每一个外角的度数是:
如图,从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向. 在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和等于一个周角,所以多边形的外角和等于360°.
多边形的外角和等于360°
结论:
1.如果一个多边形的每一个外角等于30°,则这个多边形的边数是( )
A. 8 B. 10 C. 12 D.14
学以致用
C
2.一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
C
3.正五边形的每一个外角等于____.每一个内角等于_____.
72°
108°
4.正十二边形的每个外角等于______.
30°
5.若一个正多边形的每个内角为144°,则这个正多边形的
边数为_____.
10
课堂小结
1.多边形的内角和公式:
(n-2)×180°.
2.多边形边数增加1,内角和增加180°
3.正多边形的每一个内角的度数:
5.多边形的外角和都等于360°
6.正多边形的每一个外角的度数是:
