2.2整式的加减(1) 课件 (共25张PPT)
文档属性
| 名称 | 2.2整式的加减(1) 课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 11:38:48 | ||
图片预览






文档简介
(共25张PPT)
沪科版 七年级上册
2.2 整式的加减 (1)
教学目标
1.理解同类项的概念
2.掌握合并同类项的法则
3.能正确的找出同类项,并会合并.
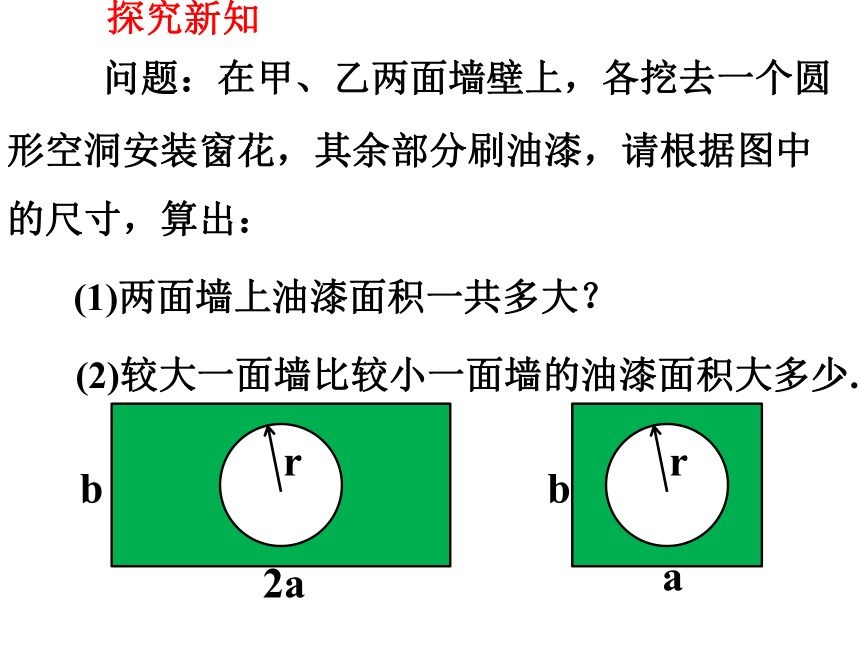
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
(2)较大一面墙比较小一面墙的油漆面积大多少.
b
b
2a
a
r
r
探究新知
b
b
2a
a
r
r
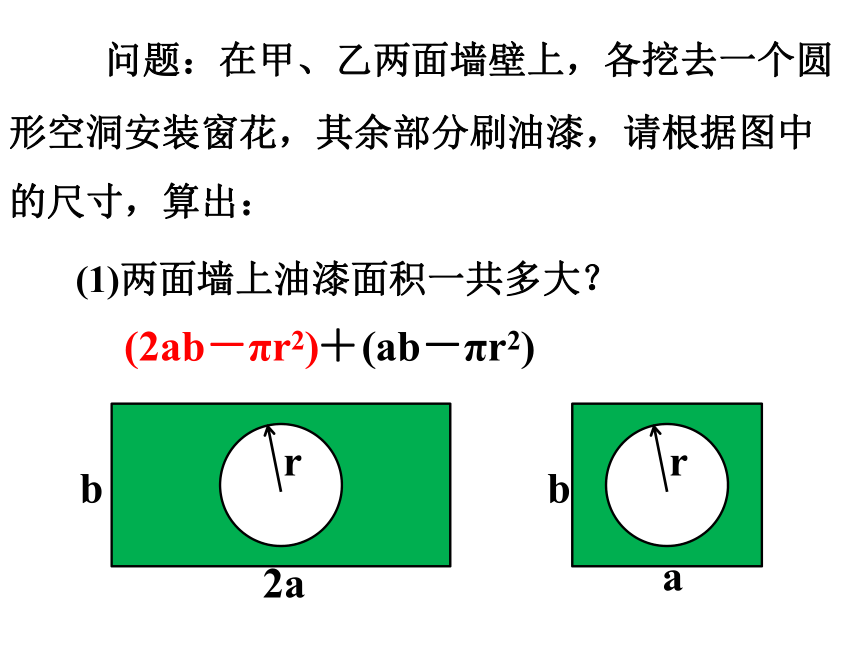
(2ab-πr2)
+
(ab-πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
b
b
2a
a
r
r
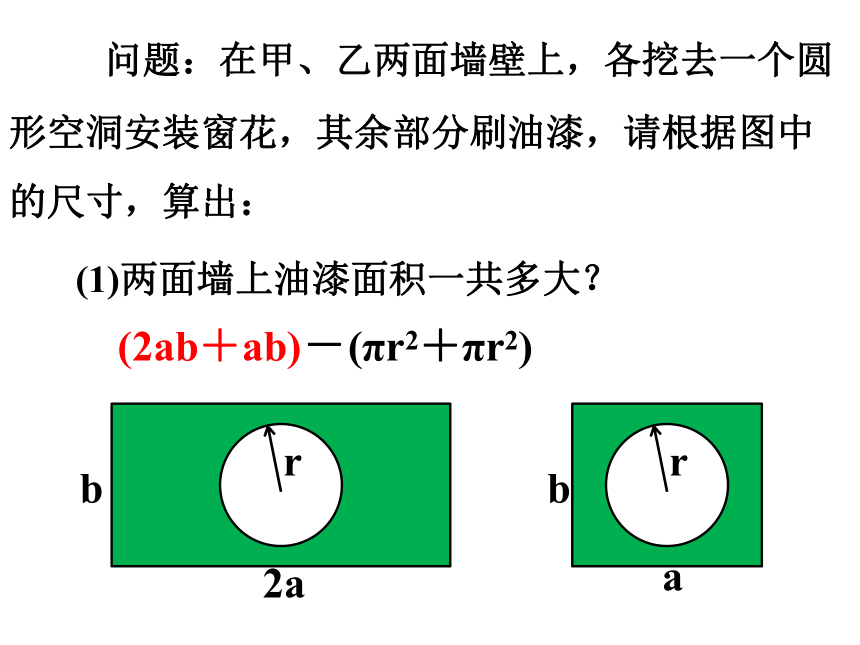
(2ab+ab)
-
(πr2+πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
b
b
2a
a
r
r
(2ab-πr2)
-
(ab-πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(2)较大一面墙比较小一面墙的油漆面积大多少?
观察多项式
(2ab+ab)-(πr2+πr2)中的项:
2ab、ab 的特点
所含字母相同并且相同字母的指数也相同的项叫做同类项.
所含字母相同
相同字母的指数也相同
常数项与常数项是同类项.
怎样判断同类项?
(1)所含字母相同;
2.两个“无关”
1.两个“相同”
(1)与系数的大小无关;
如:3abc与-cba
a3b2与b2a3
(2)相同字母的指数分别相同
(2)与所含字母的顺序无关
如:0.2ab与5ab
2x3y2与3x2y3
(2) xy与-xy ; ( )
(3) 4abc与4ac ; ( )
(1) 3a2b与3ab2 ; ( )
1. 判断下列各组中的两项是不是同类项?
×
√
×
√
(4) -3与 . ( )
1
3
练习巩固
(2) -3x2y3 与2x2
(3) 2m 与 -5n2
(1) -3a 与 6a
请你在下面的横线上填上适当的内容,使两个单项式构成同类项.
y3
n2
m
bc
bc
m
m
你能将多项式2ab+3ab进行变形吗?
(逆用乘法分配律)
( )ab
2ab+3ab=
=5ab
2
+3
同类项能合并在一起
把多项式中的同类项合并成一项,
叫做合并同类项。
在多项式中遇到同类项,可以运用加法交换律、加法结合律、乘法分配律合并.
4x2+2x-1-3x2+3x+2
=
4x2
-3x2
+2x
+3x
-1
+2
=
(4-3)
x2
+
(2+3 )
x
+
(-1+2)
=
x2
+
5
x
+
1
=
(4x2-3x2)
+(2x+3x)
+
(-1+2)
(乘法分配律)
(加法交换律)
(加法结合律)
合并同类项法则:
同类项的系数相加,所得结果作为系数,
字母和字母的指数不变.
4x2+2x-1-3x2+3x+2
=
(4-3)
x2
+
(2+3)x
+
(-1+2)
=
x2
+
5x
+
1
例1 合并下式中的同类项
4a2+3b2-2ab-3a2+b2
解:
4a2+3b2-2ab-3a2+b2
=
( )
4a2
-3a2
+
( )
3b2
+b2
-2ab
=
( )
a2
+
( )
b2
-2ab
=
a2
+
4b2
-2ab
4-3
3+1
(4) 16xy-16yx=0 . ( )
(2) 5x+2x=7x2 . ( )
(3) 5x2-3x2=2. ( )
(1) 5x2+6x2=11x4 . ( )
2 .判断下面合并同类项是否正确,
若有错, 请改正:
×
√
×
×
11x2
7x
2x2
3.合并下列各式中的同类项
(1) -8x+8x= ;
(2) -a-7a+3a= .
-1-7+3
( )
a
( )
-8+8
x
0
-5a
b
b
2a
a
r
r
(2ab+ab)
-
(πr2+πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
=3ab
-2πr2
( )
( )
例2 求多项式3a+abc- c2-3a+ c2的值,
其中a=- ,b=2,c=-3.
3a+abc- c2-3a+ c2
解:
1
3
1
3
1
3
1
3
1
6
=
3a
-3a
+abc
+
- c2+ c2
1
3
1
3
=
abc
当a= - ,b=2,c=-3时,
1
6
原式=
-
×2
×
(-3)
1
6
=1.
( )
( )
( )
求值:3x-4x2+7-3x+2x2+1,
其中x=2.
解:
3x-4x2+7-3x+2x2+1
=
( )
-3x
-4x2
+2x2
7+1
+1
=
(3-3)
x
+
3x
+
+
( )
-4
+2
x2
+
+7
=
-2
x2
+
8
当x=2时,
原式=
-2×
22
+8
=-8
+8
=0
练习 合并同类项
(1) 3x-2y+1+3y-2x-5
解:
(1)原式=
3x-2x-2y+3y+1-5
=
( 3-2)x
+
(-2+3 )y
+
(1-5 )
=
x
+
y
-4
练习 合并同类项
(2) 3x2y-2xy2+xy2-yx2
(2)原式=
( )
3x2y
-yx2
+
-2xy2
+xy2
( )
=
(3-1)
x2y
+
( )
-2+1
xy2
=
2
x2y
-
xy2
课堂小结
(1)本节课学了哪些主要内容?
(2)你能举例说明同类项的概念吗?
(3)举例说明合并同类项的方法.
(4)本节课主要运用了什么思想方法研究问题?
今天作业
课本P76第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
2.2 整式的加减 (1)
教学目标
1.理解同类项的概念
2.掌握合并同类项的法则
3.能正确的找出同类项,并会合并.
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
(2)较大一面墙比较小一面墙的油漆面积大多少.
b
b
2a
a
r
r
探究新知
b
b
2a
a
r
r
(2ab-πr2)
+
(ab-πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
b
b
2a
a
r
r
(2ab+ab)
-
(πr2+πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
b
b
2a
a
r
r
(2ab-πr2)
-
(ab-πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(2)较大一面墙比较小一面墙的油漆面积大多少?
观察多项式
(2ab+ab)-(πr2+πr2)中的项:
2ab、ab 的特点
所含字母相同并且相同字母的指数也相同的项叫做同类项.
所含字母相同
相同字母的指数也相同
常数项与常数项是同类项.
怎样判断同类项?
(1)所含字母相同;
2.两个“无关”
1.两个“相同”
(1)与系数的大小无关;
如:3abc与-cba
a3b2与b2a3
(2)相同字母的指数分别相同
(2)与所含字母的顺序无关
如:0.2ab与5ab
2x3y2与3x2y3
(2) xy与-xy ; ( )
(3) 4abc与4ac ; ( )
(1) 3a2b与3ab2 ; ( )
1. 判断下列各组中的两项是不是同类项?
×
√
×
√
(4) -3与 . ( )
1
3
练习巩固
(2) -3x2y3 与2x2
(3) 2m 与 -5n2
(1) -3a 与 6a
请你在下面的横线上填上适当的内容,使两个单项式构成同类项.
y3
n2
m
bc
bc
m
m
你能将多项式2ab+3ab进行变形吗?
(逆用乘法分配律)
( )ab
2ab+3ab=
=5ab
2
+3
同类项能合并在一起
把多项式中的同类项合并成一项,
叫做合并同类项。
在多项式中遇到同类项,可以运用加法交换律、加法结合律、乘法分配律合并.
4x2+2x-1-3x2+3x+2
=
4x2
-3x2
+2x
+3x
-1
+2
=
(4-3)
x2
+
(2+3 )
x
+
(-1+2)
=
x2
+
5
x
+
1
=
(4x2-3x2)
+(2x+3x)
+
(-1+2)
(乘法分配律)
(加法交换律)
(加法结合律)
合并同类项法则:
同类项的系数相加,所得结果作为系数,
字母和字母的指数不变.
4x2+2x-1-3x2+3x+2
=
(4-3)
x2
+
(2+3)x
+
(-1+2)
=
x2
+
5x
+
1
例1 合并下式中的同类项
4a2+3b2-2ab-3a2+b2
解:
4a2+3b2-2ab-3a2+b2
=
( )
4a2
-3a2
+
( )
3b2
+b2
-2ab
=
( )
a2
+
( )
b2
-2ab
=
a2
+
4b2
-2ab
4-3
3+1
(4) 16xy-16yx=0 . ( )
(2) 5x+2x=7x2 . ( )
(3) 5x2-3x2=2. ( )
(1) 5x2+6x2=11x4 . ( )
2 .判断下面合并同类项是否正确,
若有错, 请改正:
×
√
×
×
11x2
7x
2x2
3.合并下列各式中的同类项
(1) -8x+8x= ;
(2) -a-7a+3a= .
-1-7+3
( )
a
( )
-8+8
x
0
-5a
b
b
2a
a
r
r
(2ab+ab)
-
(πr2+πr2)
问题:在甲、乙两面墙壁上,各挖去一个圆形空洞安装窗花,其余部分刷油漆,请根据图中的尺寸,算出:
(1)两面墙上油漆面积一共多大?
=3ab
-2πr2
( )
( )
例2 求多项式3a+abc- c2-3a+ c2的值,
其中a=- ,b=2,c=-3.
3a+abc- c2-3a+ c2
解:
1
3
1
3
1
3
1
3
1
6
=
3a
-3a
+abc
+
- c2+ c2
1
3
1
3
=
abc
当a= - ,b=2,c=-3时,
1
6
原式=
-
×2
×
(-3)
1
6
=1.
( )
( )
( )
求值:3x-4x2+7-3x+2x2+1,
其中x=2.
解:
3x-4x2+7-3x+2x2+1
=
( )
-3x
-4x2
+2x2
7+1
+1
=
(3-3)
x
+
3x
+
+
( )
-4
+2
x2
+
+7
=
-2
x2
+
8
当x=2时,
原式=
-2×
22
+8
=-8
+8
=0
练习 合并同类项
(1) 3x-2y+1+3y-2x-5
解:
(1)原式=
3x-2x-2y+3y+1-5
=
( 3-2)x
+
(-2+3 )y
+
(1-5 )
=
x
+
y
-4
练习 合并同类项
(2) 3x2y-2xy2+xy2-yx2
(2)原式=
( )
3x2y
-yx2
+
-2xy2
+xy2
( )
=
(3-1)
x2y
+
( )
-2+1
xy2
=
2
x2y
-
xy2
课堂小结
(1)本节课学了哪些主要内容?
(2)你能举例说明同类项的概念吗?
(3)举例说明合并同类项的方法.
(4)本节课主要运用了什么思想方法研究问题?
今天作业
课本P76第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
