22.1 比例线段(5)课件(共20张PPT)
文档属性
| 名称 | 22.1 比例线段(5)课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 974.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 22:00:45 | ||
图片预览





文档简介
(共20张PPT)
沪科版 九年级上册
22.1 比例线段(5)
教学目标
1. 掌握平行线分线段成比例定理及推论.
2. 能够利用平行线分线段成比例定理任意等分一条已知线段,进一步培养学生的作图能力.
3. 通过定理的变式图形,进一步提高学生分析问题和解决问题的能力.
教学重点:平行线分线段成比例定理及推论.
教学难点:平行线分线段成比例定理应用.
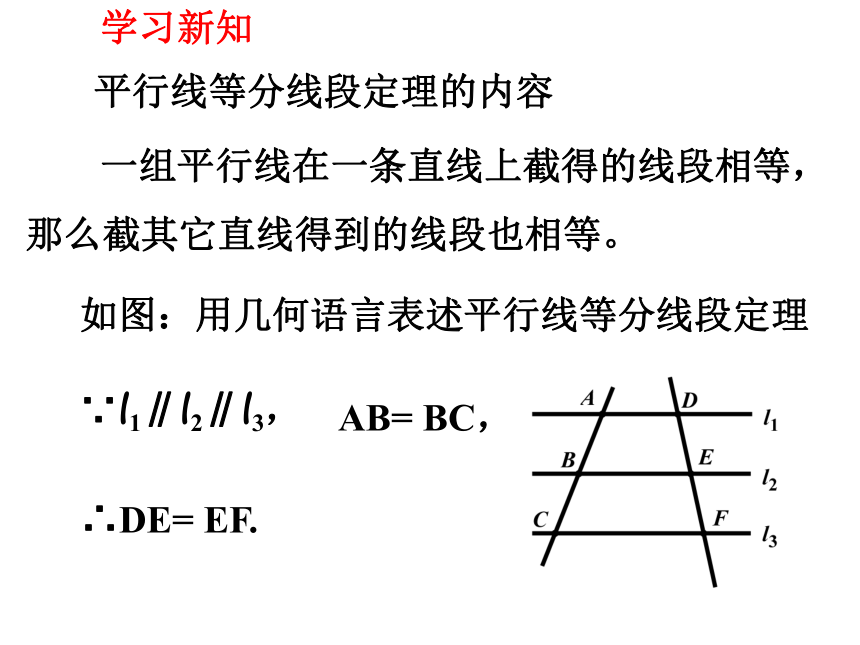
平行线等分线段定理的内容
一组平行线在一条直线上截得的线段相等,那么截其它直线得到的线段也相等。
如图:用几何语言表述平行线等分线段定理
∵l1∥l2∥l3,
AB= BC,
∴DE= EF.
学习新知
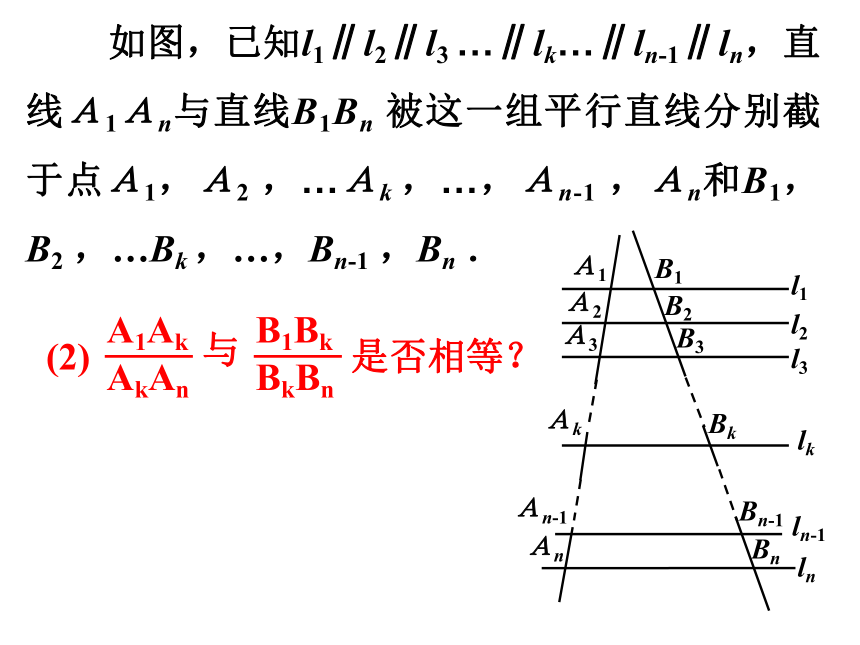
如图,已知l1∥l2∥l3 …∥lk…∥ln-1∥ln,直线A1An与直线B1Bn 被这一组平行直线分别截于点A1,A2 ,…Ak ,…,An-1 ,An和B1,B2 ,…Bk ,…,Bn-1 ,Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
(1) 如A1A2 =A2A3 =…=An-1An,
那么B1B2 , B2B3 , …,Bn-1Bn是否相等?
B1B2 = B2B3 = …=Bn-1Bn
如图,已知l1∥l2∥l3 …∥lk…∥ln-1∥ln,直线A1An与直线B1Bn 被这一组平行直线分别截于点A1,A2 ,…Ak ,…,An-1 ,An和B1,B2 ,…Bk ,…,Bn-1 ,Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
A1Ak
AkAn
与
(2)
B1Bk
BkBn
是否相等?
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
A1Ak
AkAn
与
(2)
B1Bk
BkBn
是否相等?
设A1A2 =A2A3 =…=An-1An=a,
B1B2 = B2B3 = …=Bn-1Bn=b.
则A1Ak
AkAn
=(n-k)a,
=(k-1)a,
B1Bk
=(n-k)b.
=(k-1)b,
BkBn
∴
A1Ak
AkAn
=
(n-k)a
(k-1)a
=
n-k
k-1
B1Bk
BkBn
=
(n-k)b
(k-1)b
=
n-k
k-1
∴
A1Ak
AkAn
B1Bk
BkBn
=
如图,已知l1∥l2∥l3 …∥lk…∥ln-1∥ln,直线A1An与直线B1Bn 被这一组平行直线分别截于点A1,A2 ,…Ak ,…,An-1 ,An和B1,B2 ,…Bk ,…,Bn-1 ,Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
A1Ak
AkAn
=
B1Bk
BkBn
定理:
两条直线被一组平行线所截,
所得的对应线段成比例.
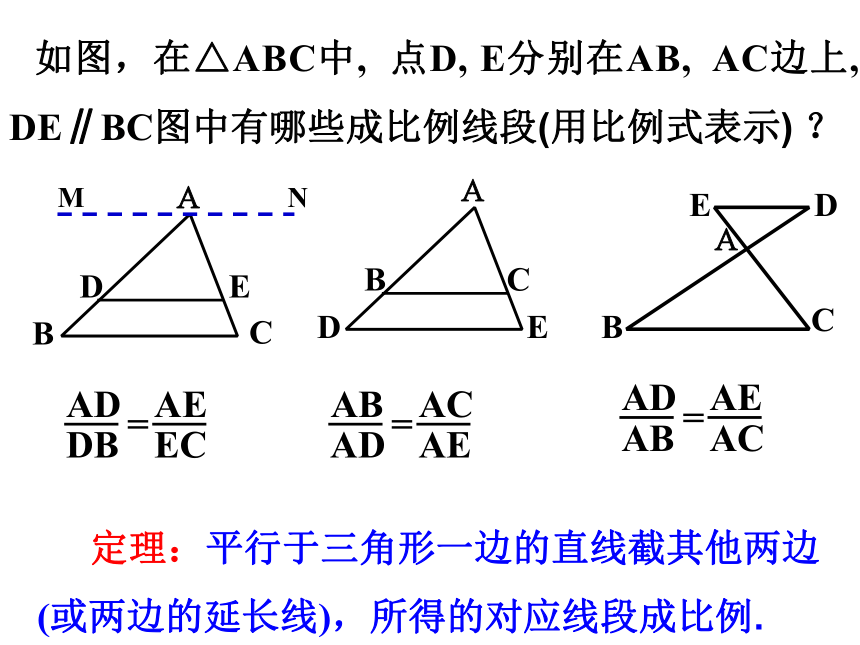
如图,在△ABC中, 点D, E分别在AB, AC边上, DE∥BC图中有哪些成比例线段(用比例式表示) ?
A
B
C
D
E
M
N
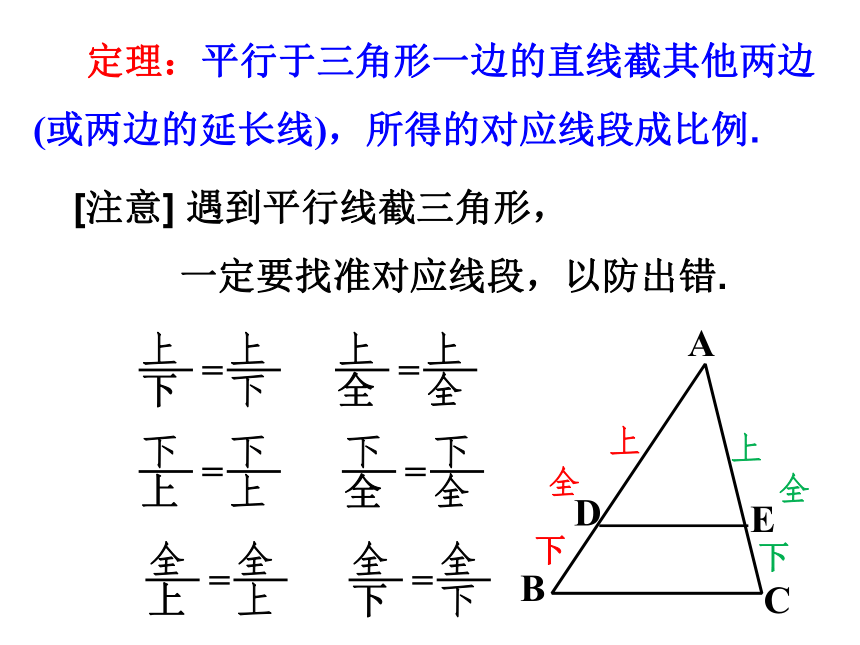
定理:平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段成比例.
A
D
E
B
C
A
D
E
B
C
AD
DB
EC
AE
=
AB
AD
AE
AC
=
AD
AB
AC
AE
=
A
B
C
D
E
[注意] 遇到平行线截三角形,
一定要找准对应线段,以防出错.
上
下
下
上
=
全
下
下
全
=
上
全
全
上
=
全
上
上
全
=
下
上
上
下
=
下
全
全
下
=
定理:平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段成比例.
上
下
上
下
全
全
例1. 如图,已知DE∥BC,AB=15,AC=10,
BD=6. 求AE的长.
A
B
C
D
E
[解析] 要求线段AE的长
要求CE的长
CE
AC
AB
BD
=
DE∥BC
例题解析
例1. 如图,已知DE∥BC,AB=15,AC=10,
BD=6. 求AE的长.
A
B
C
D
E
CE
AC
AB
BD
=
∵ DE∥BC
解:
∴
∵AB=15,AC=10, BD=6,
CE
10
15
6
∴
=
∴15CE=60
∴AE=
AC-CE
=10-4=6
∴CE=4
例1. 如图,已知DE∥BC,AB=15,AC=10,
BD=6. 求AE的长.
A
B
C
D
E
AE
AC
AB
AD
=
∵ DE∥BC
解:
∴
∵AB=15,AC=10, BD=6,
AE
10
15
9
∴
=
∴15AE=90
∴AD=
AB-BD
=15-6=9.
∴AE=6.
解法二
1.如图,在△ABC中,点D,E分别在AB, AC边上,DE∥BC,若AD∶AB=3∶4,AE=6,则AC等于 ( ).
A.3 B.4 C.6 D.8
A
B
C
D
E
D
AE
AC
AB
AD
=
∵ DE∥BC
∴
6
AC
4
3
∴
=
∴3AC=24
∴AC=8
练习巩固
2.如图,在△ABC中,DE∥BC,AD=2cm,
AB=6 cm,AE=1.5 cm,则EC=______.
3 cm
A
B
C
D
E
AD
AB
AC
AE
=
∵ DE∥BC
∴
2
6
AC
1.5
∴
=
∴2AC=9
∴EC=
AC-AE
=4.5-1.5=3
∴AC=4.5
3.如图,已知AB∥DE,AE与DB交于点C,
AC=3,BC=2,CD=4,则CE= .
6
A
B
C
D
E
CE
AC
BC
CD
=
∵ AB∥DE
∴
CE
3
2
4
∴
=
∴CE=6
1.5
4.5
A
D
B
E
F
C
l1
l2
l3
∵已知l1∥l2∥l3
BC
AB
DE
EF
=
∴
BC
3
4
2
∴
=
∴BC=1.5
∴AC=
AB+BC
=3+1.5=4.5
如图(1),已知l1∥l2∥l3 .
(1)
D
A
E
B
C
F
l1
l2
l3
.
则
;
;
A
B
C
D
E
定理:平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例.
A
D
E
B
C
A
D
E
B
C
定理:组平行线截两条直线,所得的对应线段成比例.
DE
EF
DE
DF
EF
DF
今天作业
课本P71页第1、2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.1 比例线段(5)
教学目标
1. 掌握平行线分线段成比例定理及推论.
2. 能够利用平行线分线段成比例定理任意等分一条已知线段,进一步培养学生的作图能力.
3. 通过定理的变式图形,进一步提高学生分析问题和解决问题的能力.
教学重点:平行线分线段成比例定理及推论.
教学难点:平行线分线段成比例定理应用.
平行线等分线段定理的内容
一组平行线在一条直线上截得的线段相等,那么截其它直线得到的线段也相等。
如图:用几何语言表述平行线等分线段定理
∵l1∥l2∥l3,
AB= BC,
∴DE= EF.
学习新知
如图,已知l1∥l2∥l3 …∥lk…∥ln-1∥ln,直线A1An与直线B1Bn 被这一组平行直线分别截于点A1,A2 ,…Ak ,…,An-1 ,An和B1,B2 ,…Bk ,…,Bn-1 ,Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
(1) 如A1A2 =A2A3 =…=An-1An,
那么B1B2 , B2B3 , …,Bn-1Bn是否相等?
B1B2 = B2B3 = …=Bn-1Bn
如图,已知l1∥l2∥l3 …∥lk…∥ln-1∥ln,直线A1An与直线B1Bn 被这一组平行直线分别截于点A1,A2 ,…Ak ,…,An-1 ,An和B1,B2 ,…Bk ,…,Bn-1 ,Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
A1Ak
AkAn
与
(2)
B1Bk
BkBn
是否相等?
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
A1Ak
AkAn
与
(2)
B1Bk
BkBn
是否相等?
设A1A2 =A2A3 =…=An-1An=a,
B1B2 = B2B3 = …=Bn-1Bn=b.
则A1Ak
AkAn
=(n-k)a,
=(k-1)a,
B1Bk
=(n-k)b.
=(k-1)b,
BkBn
∴
A1Ak
AkAn
=
(n-k)a
(k-1)a
=
n-k
k-1
B1Bk
BkBn
=
(n-k)b
(k-1)b
=
n-k
k-1
∴
A1Ak
AkAn
B1Bk
BkBn
=
如图,已知l1∥l2∥l3 …∥lk…∥ln-1∥ln,直线A1An与直线B1Bn 被这一组平行直线分别截于点A1,A2 ,…Ak ,…,An-1 ,An和B1,B2 ,…Bk ,…,Bn-1 ,Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
l1
Bk
Bn
Bn-1
l2
l3
lk
ln
ln-1
A1Ak
AkAn
=
B1Bk
BkBn
定理:
两条直线被一组平行线所截,
所得的对应线段成比例.
如图,在△ABC中, 点D, E分别在AB, AC边上, DE∥BC图中有哪些成比例线段(用比例式表示) ?
A
B
C
D
E
M
N
定理:平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段成比例.
A
D
E
B
C
A
D
E
B
C
AD
DB
EC
AE
=
AB
AD
AE
AC
=
AD
AB
AC
AE
=
A
B
C
D
E
[注意] 遇到平行线截三角形,
一定要找准对应线段,以防出错.
上
下
下
上
=
全
下
下
全
=
上
全
全
上
=
全
上
上
全
=
下
上
上
下
=
下
全
全
下
=
定理:平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段成比例.
上
下
上
下
全
全
例1. 如图,已知DE∥BC,AB=15,AC=10,
BD=6. 求AE的长.
A
B
C
D
E
[解析] 要求线段AE的长
要求CE的长
CE
AC
AB
BD
=
DE∥BC
例题解析
例1. 如图,已知DE∥BC,AB=15,AC=10,
BD=6. 求AE的长.
A
B
C
D
E
CE
AC
AB
BD
=
∵ DE∥BC
解:
∴
∵AB=15,AC=10, BD=6,
CE
10
15
6
∴
=
∴15CE=60
∴AE=
AC-CE
=10-4=6
∴CE=4
例1. 如图,已知DE∥BC,AB=15,AC=10,
BD=6. 求AE的长.
A
B
C
D
E
AE
AC
AB
AD
=
∵ DE∥BC
解:
∴
∵AB=15,AC=10, BD=6,
AE
10
15
9
∴
=
∴15AE=90
∴AD=
AB-BD
=15-6=9.
∴AE=6.
解法二
1.如图,在△ABC中,点D,E分别在AB, AC边上,DE∥BC,若AD∶AB=3∶4,AE=6,则AC等于 ( ).
A.3 B.4 C.6 D.8
A
B
C
D
E
D
AE
AC
AB
AD
=
∵ DE∥BC
∴
6
AC
4
3
∴
=
∴3AC=24
∴AC=8
练习巩固
2.如图,在△ABC中,DE∥BC,AD=2cm,
AB=6 cm,AE=1.5 cm,则EC=______.
3 cm
A
B
C
D
E
AD
AB
AC
AE
=
∵ DE∥BC
∴
2
6
AC
1.5
∴
=
∴2AC=9
∴EC=
AC-AE
=4.5-1.5=3
∴AC=4.5
3.如图,已知AB∥DE,AE与DB交于点C,
AC=3,BC=2,CD=4,则CE= .
6
A
B
C
D
E
CE
AC
BC
CD
=
∵ AB∥DE
∴
CE
3
2
4
∴
=
∴CE=6
1.5
4.5
A
D
B
E
F
C
l1
l2
l3
∵已知l1∥l2∥l3
BC
AB
DE
EF
=
∴
BC
3
4
2
∴
=
∴BC=1.5
∴AC=
AB+BC
=3+1.5=4.5
如图(1),已知l1∥l2∥l3 .
(1)
D
A
E
B
C
F
l1
l2
l3
.
则
;
;
A
B
C
D
E
定理:平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例.
A
D
E
B
C
A
D
E
B
C
定理:组平行线截两条直线,所得的对应线段成比例.
DE
EF
DE
DF
EF
DF
今天作业
课本P71页第1、2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
