22.1 比例线段(1) 课件(共27张PPT)
文档属性
| 名称 | 22.1 比例线段(1) 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 16:15:16 | ||
图片预览







文档简介
(共27张PPT)
沪科版 九年级上册
22.1 比例线段(1)
教学目标:
1.理解相似多边形的概念.
2.理解相似多边形的相似比(相似系数)的概念.
教学重点:相似多边形及相似比的概念.
教学难点:相似比.
现实生活中的相似
现实生活中的相似
现实生活中的相似
现实生活中的相似
定义: 我们把这些形状相同的图形
叫做相似图形.
学习新知
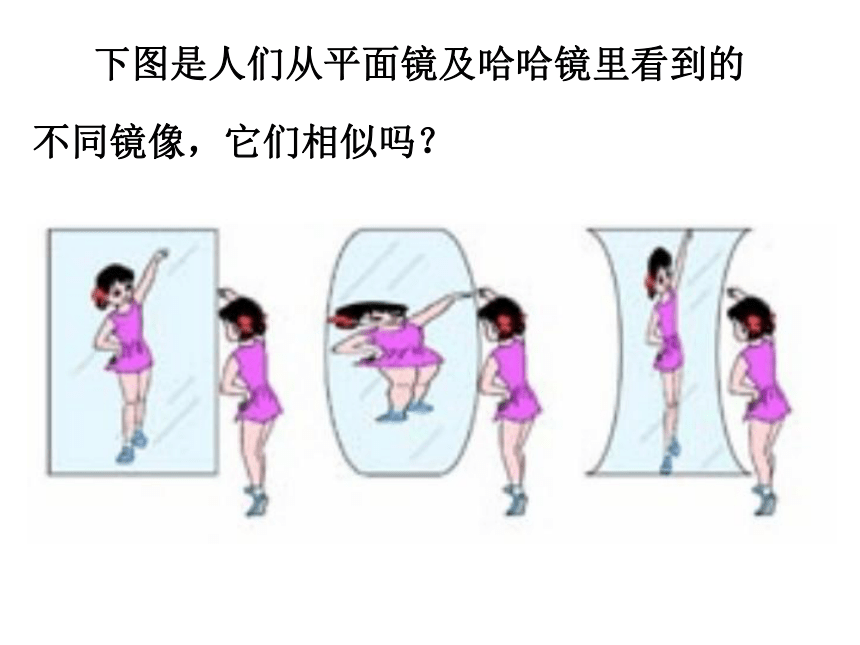
下图是人们从平面镜及哈哈镜里看到的
不同镜像,它们相似吗?
相似
练习巩固
观察下面的图形(a)~(g),其中哪些是与(1)、(2)或(3)相似的?
(a )与(1)、
(d)与(2)、
(g)与(3).
1.6
A
B
C
D
A1
D1
B1
C1
3.2
(1)
对应角有什么关系?
∠A=∠A1 ,∠ B= ∠ B1,
∠C=∠C1 ,∠ D= ∠D1.
对应边有什么关系?
BC
B1C1
=
AB
A1B1
=
CD
C1D1
=
DA
D1A1
=
1.6
3.2
=
1
2
两个正方形
学习新知
对应角有什么关系?
∠A=∠A1 ,∠ B= ∠ B1,
∠C=∠C1 .
对应边有什么关系?
BC
B1C1
=
AB
A1B1
=
CA
C1A1
=
2
4
=
1
2
两个等边三角形
B1
C1
A1
4
B
C
2
A
(2)
相似多边形
各对应角相等、各对应边成的比相等的多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
相似多边形
对应角相等,对应边的比相等
相似比
相似多边形对应边的比叫做相似比.
(k > 0)
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
BC
B1C1
=
AB
A1B1
=
CD
C1D1
=
DE
D1E1
=
EF
E1F1
=
FA
F1A1
=
k
全等是一种特殊的相似。
当相似比k =1时,
相似图形即是全等图形。
课堂小结:
1. 两个边数相同的多边形,如果它们的__________相等,______________也相等,那么这两个多边形叫做相似多边形.
2. 相似多边形________________叫做相似比或相似系数.
3. 判定两个图形相似抓住图形的本质——___________.
1. 判断:
(1)任意两个矩形都是相似图形( )
(2)任意两个圆形是相似图形( )
(3)对应角相等的两个四边形是相似多边形( )
(4)两个正五边形是相似多边形( )
(5)两个全等三角形是相似多边形( )
(6)两菱形是相似多边形( )
(7)两个相似多边形,对应边的比相等( )
√
√
√
×
√
×
×
练习巩固
2. 如图,矩形ABCD与矩形A1B1C1D1相似吗?
为什么?
B1
A1
D1
C1
1.5
2
A
D
C
B
1
3
解:矩形ABCD与矩形A1B1C1D1不相似.
∵
∴它们对应边的比不相等.
BC
B1C1
=
AB
A1B1
=
3
2
2
3
=
1
1.5
3. 如图,菱形ABCD与菱形A1B1C1D1相似吗?
为什么?
A
D
C
B
解:菱形ABCD与菱形A1B1C1D1不相似.
∴它们对应角不相等.
B1
A1
D1
C1
45°
60°
∵∠A=60°,
∠A1=45°,
4. 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
∠β=
∴ ∠α=
解: ∵四边形ABCD和EFGH相似,
∠C=83°,
∠A=
∠E=118°,
360°-(78°+83°+118°)
=81°.
∴它们的对应角相等.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
∵四边形ABCD和EFGH相似,
∴ x=28(cm).
∴它们的对应边的比相等.
EH
AD
=
AB
EF
x
21
=
24
18
∴
5. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示可知,两图形的相似比为:
∴
∴ b = 4.5,
∴ a = 3,
∴ c = 4,
∴ d = 6.
5
7.5
=
2
3
2
3
=
2
a
2
3
=
3
b
c
6
=
2
3
d
9
=
2
3
6.如图,点E、F分别是矩形ABCD的边AD、
BC的中点,若矩形ABCD与矩形EABF相似,
AB=1,求矩形ABCD的面积.
A
B
C
D
E
F
解:∵矩形ABCD与矩形EABF 相似
∵E是AD的中点,
AB
AE
=
BC
AB
∴
∴ AB2=
BC
·
AE
∴AE= AD
=
1
2
1
2
BC
∴ AB2=
1
2
BC2
∴ 12=
1
2
BC2
今天作业
课本P72页第3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.1 比例线段(1)
教学目标:
1.理解相似多边形的概念.
2.理解相似多边形的相似比(相似系数)的概念.
教学重点:相似多边形及相似比的概念.
教学难点:相似比.
现实生活中的相似
现实生活中的相似
现实生活中的相似
现实生活中的相似
定义: 我们把这些形状相同的图形
叫做相似图形.
学习新知
下图是人们从平面镜及哈哈镜里看到的
不同镜像,它们相似吗?
相似
练习巩固
观察下面的图形(a)~(g),其中哪些是与(1)、(2)或(3)相似的?
(a )与(1)、
(d)与(2)、
(g)与(3).
1.6
A
B
C
D
A1
D1
B1
C1
3.2
(1)
对应角有什么关系?
∠A=∠A1 ,∠ B= ∠ B1,
∠C=∠C1 ,∠ D= ∠D1.
对应边有什么关系?
BC
B1C1
=
AB
A1B1
=
CD
C1D1
=
DA
D1A1
=
1.6
3.2
=
1
2
两个正方形
学习新知
对应角有什么关系?
∠A=∠A1 ,∠ B= ∠ B1,
∠C=∠C1 .
对应边有什么关系?
BC
B1C1
=
AB
A1B1
=
CA
C1A1
=
2
4
=
1
2
两个等边三角形
B1
C1
A1
4
B
C
2
A
(2)
相似多边形
各对应角相等、各对应边成的比相等的多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
相似多边形
对应角相等,对应边的比相等
相似比
相似多边形对应边的比叫做相似比.
(k > 0)
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
BC
B1C1
=
AB
A1B1
=
CD
C1D1
=
DE
D1E1
=
EF
E1F1
=
FA
F1A1
=
k
全等是一种特殊的相似。
当相似比k =1时,
相似图形即是全等图形。
课堂小结:
1. 两个边数相同的多边形,如果它们的__________相等,______________也相等,那么这两个多边形叫做相似多边形.
2. 相似多边形________________叫做相似比或相似系数.
3. 判定两个图形相似抓住图形的本质——___________.
1. 判断:
(1)任意两个矩形都是相似图形( )
(2)任意两个圆形是相似图形( )
(3)对应角相等的两个四边形是相似多边形( )
(4)两个正五边形是相似多边形( )
(5)两个全等三角形是相似多边形( )
(6)两菱形是相似多边形( )
(7)两个相似多边形,对应边的比相等( )
√
√
√
×
√
×
×
练习巩固
2. 如图,矩形ABCD与矩形A1B1C1D1相似吗?
为什么?
B1
A1
D1
C1
1.5
2
A
D
C
B
1
3
解:矩形ABCD与矩形A1B1C1D1不相似.
∵
∴它们对应边的比不相等.
BC
B1C1
=
AB
A1B1
=
3
2
2
3
=
1
1.5
3. 如图,菱形ABCD与菱形A1B1C1D1相似吗?
为什么?
A
D
C
B
解:菱形ABCD与菱形A1B1C1D1不相似.
∴它们对应角不相等.
B1
A1
D1
C1
45°
60°
∵∠A=60°,
∠A1=45°,
4. 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
∠β=
∴ ∠α=
解: ∵四边形ABCD和EFGH相似,
∠C=83°,
∠A=
∠E=118°,
360°-(78°+83°+118°)
=81°.
∴它们的对应角相等.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
∵四边形ABCD和EFGH相似,
∴ x=28(cm).
∴它们的对应边的比相等.
EH
AD
=
AB
EF
x
21
=
24
18
∴
5. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示可知,两图形的相似比为:
∴
∴ b = 4.5,
∴ a = 3,
∴ c = 4,
∴ d = 6.
5
7.5
=
2
3
2
3
=
2
a
2
3
=
3
b
c
6
=
2
3
d
9
=
2
3
6.如图,点E、F分别是矩形ABCD的边AD、
BC的中点,若矩形ABCD与矩形EABF相似,
AB=1,求矩形ABCD的面积.
A
B
C
D
E
F
解:∵矩形ABCD与矩形EABF 相似
∵E是AD的中点,
AB
AE
=
BC
AB
∴
∴ AB2=
BC
·
AE
∴AE= AD
=
1
2
1
2
BC
∴ AB2=
1
2
BC2
∴ 12=
1
2
BC2
今天作业
课本P72页第3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
