22.1 比例线段(3)课件(共20张PPT)
文档属性
| 名称 | 22.1 比例线段(3)课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-30 22:03:35 | ||
图片预览








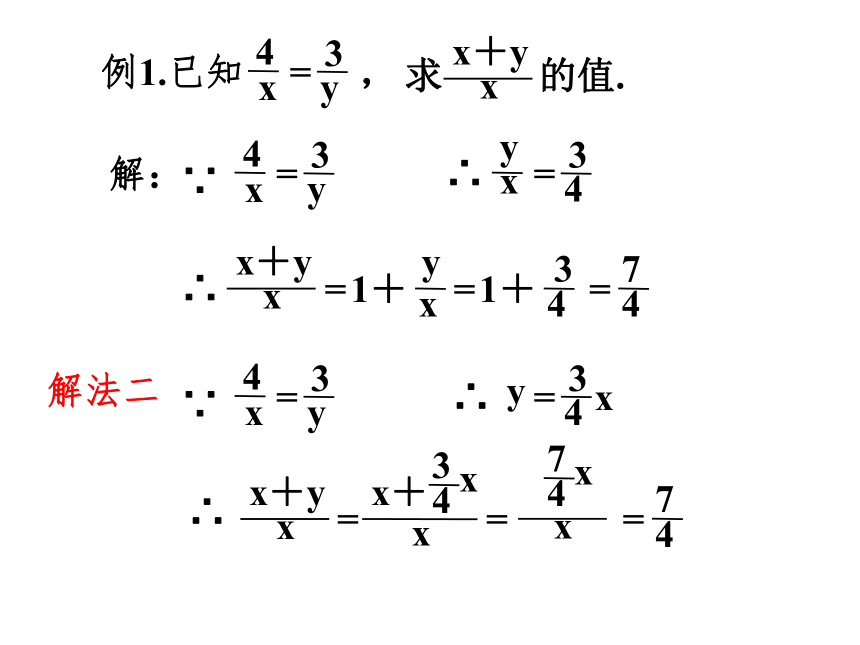
文档简介
(共20张PPT)
沪科版 九年级上册
22.1 比例线段(3)
教学目标:
1.能熟记比例的基本性质、合分比性质和等比性质.
2.能应用上述性质解决有关实际问题.
3.通过结合图形,运用比例的性质来证明有关问题,培养学生数形相结合的思想和逻辑推理的能力.
教学重点:比例的性质应用.
教学难点:比例性质的灵活应用.
复习引入
1.判断下列四条线段是否是成比例线段:
(1)
(2)
a=4,b=6,c=5,d=10
a=2,b= ,c=2 ,d=5
5
5
5
解: (1)
∵ d>b>c>a
∴
d
b
10
6
=
c
a
5
4
=
d
b
c
a
≠
∴ a、b、c、d不是成比例线段.
5
3
=
复习引入
1.判断下列四条线段是否是成比例线段:
(1)
(2)
a=4,b=6,c=5,d=10
a=2,b= ,c=2 ,d=5
5
15
3
解: (2)
∵ d>c>b>a
∴
d
c
=
b
a
2
=
d
c
b
a
=
∴ a、b、c、d是成比例线段.
2
=
3
5
15
2
5
5
在四条线段a,b,c,d中,如果其中两条线段a,b的比,等于另外两条线段c,d的比,
即
那么,
这四条线段叫做成比例线段,
简称比例线段.
或
a
b
=
c
d
∵ a:b=c:d,
∴ ad=bc
(或a:b=c:d),
a
b
=
c
d
∵
∴ ad=bc
学习新知
1.比例线段的性质.
或如果 a:b=c:d,
那么 ad=bc.
a
b
=
c
d
如果 ,
那么 ad=bc.
(1)基本性质
(b、d≠0),
如果ad=bc,
a
c
=
b
d
那么 .
a
b
=
c
d
那么 .
d
b
=
c
a
那么 .
b
a
=
d
c
那么 .
1.比例线段的性质.
a
b
=
c
d
如果 ,
那么 .
(2)合比性质
(b、d≠0).
a±b
b
=
c±d
d
a
b
=
c
d
∵
a
b
=
c
d
∴
±1
±1,
a
b
=
c
d
∴
±
± ,
b
b
d
d
a±b
b
=
c±d
d
∴
(3)等比性质
a1
b1
=
a2
b2
如果 ,
=
a3
b3
an
bn
= =
…
那么 .
a1+a2+a3+…+an
=
b1+b2+b3+…+bn
a1
b1
b1+b2+…+bn≠0,
a1
b1
=
a2
b2
设 =k,
an
bn
= =
…
则a1=kb1,
a1+a2+a3+…+an
=
b1+b2+b3+…+bn
kb1+kb2+…+kbn
=
b1+b2+b3+…+bn
=k
b1+b2+b3+…+bn
k(b1+b2+…+bn)
=
a1
b1
a2=kb2,
…,an=kbn
引入参数k
例1.已知 ,
4
x
=
3
y
x+y
x
求 的值.
解:
4
x
=
3
y
∵
y
x
=
3
4
∴
∴
x+
x
=
1+
y
x
=
1+
3
4
=
7
4
4
x
=
3
y
∵
y
x
=
3
4
∴
∴
x+y
x
=
x+y
x
3
4
x
=
x
7
4
x
=
7
4
解法二
例1.已知 ,
4
x
=
3
y
x+y
x
求 的值.
解:
4
x
=
3
y
∵
x
4
=
y
3
∴
4k+
4k
∴
x+y
x
=
3k
=
4k
7k
=
7
4
x
4
=
y
3
设
=k
∴
x=4k,
y=3k
引入参数k
解法三
例2.已知 ,
a-2b
b
=
5
3
a+b
b
求 的值.
解:
∵
∴
11k+
3k
∴
=
3k
=
3k
14k
=
14
3
设
=k
∴
a-2b=5k,
b=3k
a+b
b
a-2b
b
=
5
3
a-2b
5
=
b
3
a-2b
5
=
b
3
∴
a=11k,
引入参数k
例3.如果 ,
求 m的值.
解:
∵
∴
∴
a+b
c
b+c
a
=
a+c
b
=
=m
且a+b+c≠0),
a+b
c
b+c
a
=
a+c
b
=
=m
a+b+c
b+c+a+c+a+b
=m
a+b+c
2(a+b+c)
=m
∴
m=
1
2
例题解析
1.已知 ,
5x-4y=0
x+y
x
求 和 的值.
解:
∵
∴
∴
x
y
5x-4y=0
5x=4y
x
y
=
4
5
x
y
=
5
4
∴
=
1+
y
x
=
1+
5
4
=
9
4
x+y
x
练习巩固
2.已知 ,
a-b
b
=
2
3
a:b
求 的值.
解:
∵
∴
∴
=
5
3
∴
3a=5b,
a
b
a-b
b
=
2
3
3a-3b=2b,
2.已知 ,
a-b
b
=
2
3
a:b
求 的值.
解:
∵
∴
∴
=
3k
5k
=
5
3
设
=k
∴
a-b=2k,
b=3k
a
b
a-b
b
=
2
3
a-b
2
=
b
3
a-b
2
=
b
3
∴
a=5k,
引入参数k
a
b
=
c
d
3.已知 ,
=
e
f
3
5
=
求 的值 .
a+c+e
b+d+f
且b+d+f≠0,
a
b
=
c
d
∵ ,
=
e
f
3
5
=
∴
a+c+e
b+d+f
=
a
b
=
3
5
解:
课堂小结
1.比例的基本性质、合比性质和等比性质.
2.注意灵活应用比例的有关性质.
3.认真观察图形,特别注意图形中线段的和、差,巧妙地与合比性质结合起来.
今天作业
课本P72页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.1 比例线段(3)
教学目标:
1.能熟记比例的基本性质、合分比性质和等比性质.
2.能应用上述性质解决有关实际问题.
3.通过结合图形,运用比例的性质来证明有关问题,培养学生数形相结合的思想和逻辑推理的能力.
教学重点:比例的性质应用.
教学难点:比例性质的灵活应用.
复习引入
1.判断下列四条线段是否是成比例线段:
(1)
(2)
a=4,b=6,c=5,d=10
a=2,b= ,c=2 ,d=5
5
5
5
解: (1)
∵ d>b>c>a
∴
d
b
10
6
=
c
a
5
4
=
d
b
c
a
≠
∴ a、b、c、d不是成比例线段.
5
3
=
复习引入
1.判断下列四条线段是否是成比例线段:
(1)
(2)
a=4,b=6,c=5,d=10
a=2,b= ,c=2 ,d=5
5
15
3
解: (2)
∵ d>c>b>a
∴
d
c
=
b
a
2
=
d
c
b
a
=
∴ a、b、c、d是成比例线段.
2
=
3
5
15
2
5
5
在四条线段a,b,c,d中,如果其中两条线段a,b的比,等于另外两条线段c,d的比,
即
那么,
这四条线段叫做成比例线段,
简称比例线段.
或
a
b
=
c
d
∵ a:b=c:d,
∴ ad=bc
(或a:b=c:d),
a
b
=
c
d
∵
∴ ad=bc
学习新知
1.比例线段的性质.
或如果 a:b=c:d,
那么 ad=bc.
a
b
=
c
d
如果 ,
那么 ad=bc.
(1)基本性质
(b、d≠0),
如果ad=bc,
a
c
=
b
d
那么 .
a
b
=
c
d
那么 .
d
b
=
c
a
那么 .
b
a
=
d
c
那么 .
1.比例线段的性质.
a
b
=
c
d
如果 ,
那么 .
(2)合比性质
(b、d≠0).
a±b
b
=
c±d
d
a
b
=
c
d
∵
a
b
=
c
d
∴
±1
±1,
a
b
=
c
d
∴
±
± ,
b
b
d
d
a±b
b
=
c±d
d
∴
(3)等比性质
a1
b1
=
a2
b2
如果 ,
=
a3
b3
an
bn
= =
…
那么 .
a1+a2+a3+…+an
=
b1+b2+b3+…+bn
a1
b1
b1+b2+…+bn≠0,
a1
b1
=
a2
b2
设 =k,
an
bn
= =
…
则a1=kb1,
a1+a2+a3+…+an
=
b1+b2+b3+…+bn
kb1+kb2+…+kbn
=
b1+b2+b3+…+bn
=k
b1+b2+b3+…+bn
k(b1+b2+…+bn)
=
a1
b1
a2=kb2,
…,an=kbn
引入参数k
例1.已知 ,
4
x
=
3
y
x+y
x
求 的值.
解:
4
x
=
3
y
∵
y
x
=
3
4
∴
∴
x+
x
=
1+
y
x
=
1+
3
4
=
7
4
4
x
=
3
y
∵
y
x
=
3
4
∴
∴
x+y
x
=
x+y
x
3
4
x
=
x
7
4
x
=
7
4
解法二
例1.已知 ,
4
x
=
3
y
x+y
x
求 的值.
解:
4
x
=
3
y
∵
x
4
=
y
3
∴
4k+
4k
∴
x+y
x
=
3k
=
4k
7k
=
7
4
x
4
=
y
3
设
=k
∴
x=4k,
y=3k
引入参数k
解法三
例2.已知 ,
a-2b
b
=
5
3
a+b
b
求 的值.
解:
∵
∴
11k+
3k
∴
=
3k
=
3k
14k
=
14
3
设
=k
∴
a-2b=5k,
b=3k
a+b
b
a-2b
b
=
5
3
a-2b
5
=
b
3
a-2b
5
=
b
3
∴
a=11k,
引入参数k
例3.如果 ,
求 m的值.
解:
∵
∴
∴
a+b
c
b+c
a
=
a+c
b
=
=m
且a+b+c≠0),
a+b
c
b+c
a
=
a+c
b
=
=m
a+b+c
b+c+a+c+a+b
=m
a+b+c
2(a+b+c)
=m
∴
m=
1
2
例题解析
1.已知 ,
5x-4y=0
x+y
x
求 和 的值.
解:
∵
∴
∴
x
y
5x-4y=0
5x=4y
x
y
=
4
5
x
y
=
5
4
∴
=
1+
y
x
=
1+
5
4
=
9
4
x+y
x
练习巩固
2.已知 ,
a-b
b
=
2
3
a:b
求 的值.
解:
∵
∴
∴
=
5
3
∴
3a=5b,
a
b
a-b
b
=
2
3
3a-3b=2b,
2.已知 ,
a-b
b
=
2
3
a:b
求 的值.
解:
∵
∴
∴
=
3k
5k
=
5
3
设
=k
∴
a-b=2k,
b=3k
a
b
a-b
b
=
2
3
a-b
2
=
b
3
a-b
2
=
b
3
∴
a=5k,
引入参数k
a
b
=
c
d
3.已知 ,
=
e
f
3
5
=
求 的值 .
a+c+e
b+d+f
且b+d+f≠0,
a
b
=
c
d
∵ ,
=
e
f
3
5
=
∴
a+c+e
b+d+f
=
a
b
=
3
5
解:
课堂小结
1.比例的基本性质、合比性质和等比性质.
2.注意灵活应用比例的有关性质.
3.认真观察图形,特别注意图形中线段的和、差,巧妙地与合比性质结合起来.
今天作业
课本P72页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
