沪科版数学七年级上册 2.1 代数式 同步练习(含答案)
文档属性
| 名称 | 沪科版数学七年级上册 2.1 代数式 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 10:02:22 | ||
图片预览

文档简介
课后训练
基础巩固
1.下列式子符合代数式的书写格式的是( ).
A.a·40a B. C.3÷m D.
2.下列说法正确的是( ).
A.单项式m既没有系数,也没有次数 B.单项式5×105的系数是5
C.-2 010也是单项式 D.-3πx2的系数是-3
3.买a台空调花费b元,则买10台这样的空调要花费( ).
A.元 B.10ab元 C.元 D.元
4.多项式2x-3xy2+1是__________次__________项式,其中最高次项是__________,常数项是__________.
5.当x=10,y=9时,代数式x2-y2的值是__________.
6.按照下面的操作步骤,若输入x的值为3,则输出的值为__________.
7.观察一列单项式:a,-2a2,4a3,-8a4,…,根据你发现的规律,第7个单项式为__________;第n个单项式为__________.
8.用代数式表示:
(1)a与b的积的4倍;
(2)x的2倍与y的5%的差;
(3)x的倒数与m除n的商的和;
(4)a与b的差的立方;
(5)a,b两数的立方差(即立方的差);
(6)a与b差的平方的c倍.
能力提升
9.当x=2时,代数式ax3-bx-1的值为1 000,求x=-2时,代数式ax3-bx-1的值.
10.为了节约用水,某市自来水公司采取以下收费方法:每户每月用水不超过10 t,收费1.5元/t;每户每月用水超过10 t,超过的部分按3元/t收费.现在已知小明家2月份用水x t(x>10),请用代数式表示小明家2月份应交水费多少元?如果x=16,那么小明家2月份应交水费多少元?
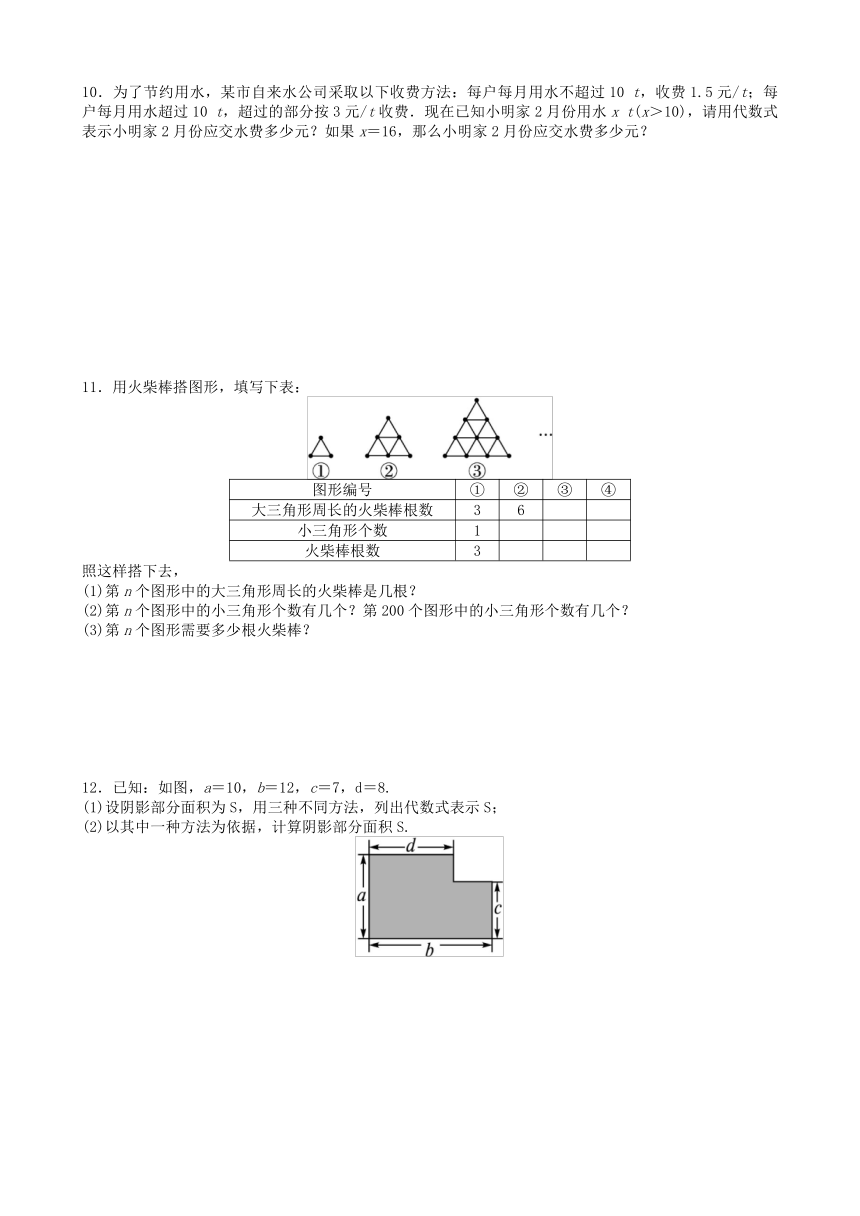
11.用火柴棒搭图形,填写下表:
图形编号 ① ② ③ ④
大三角形周长的火柴棒根数 3 6
小三角形个数 1
火柴棒根数 3
照这样搭下去,
(1)第n个图形中的大三角形周长的火柴棒是几根?
(2)第n个图形中的小三角形个数有几个?第200个图形中的小三角形个数有几个?
(3)第n个图形需要多少根火柴棒?
12.已知:如图,a=10,b=12,c=7,d=8.
(1)设阴影部分面积为S,用三种不同方法,列出代数式表示S;
(2)以其中一种方法为依据,计算阴影部分面积S.
参考答案
1.B
2.C 解析:只含有字母因式的单项式不能认为它们没有系数,它们的系数是“1”或“-1”;π,5×105,-2 010都是常数.
3.C 解析:买一台空调的花费=总价÷数量,即为元,所以买10台这样的空调要花费为10×=(元).
4.三 三 -3xy2 1 5.19
6.7 解析:实质是求当x=3时,代数式(x-5)2+3的值.
7.64a7 (-2)n-1an
8.(1)4ab;(2)2x-5%y;(3);
(4)(a-b)3;(5)a3-b3;(6)c(a-b)2.
解析:本题解题关键之一是抓住语句中的关键性词语,如:“和、差、倍、倒数、积、商、平方”等,并熟悉它们所对应的每一种运算.第二是分清运算的顺序,一般按先读先写的原则确定其先后顺序.如:(3)x的倒数与m除n的商的和.按题目中叙述的顺序分步如下:①x的倒数即;②m除n的商即;③倒数与商的和即,并要注意除和除以的区别;(4)和(5)两小题要注意二者运算顺序的不同.
9.解:把x=2代入代数式ax3-bx-1中得23a-2b-1=1 000,即8a-2b=1 001;把x=-2代入代数式ax3-bx-1中得-23a+2b-1=-8a+2b-1=-(8a-2b)-1,再把8a-2b=1 001代入得原式=-1 001-1=-1 002.
分析:(1)假设每吨水都是3元,则x t水为3x元,减去前10t水多算的15元,就是小明家2月份应交水费.(2)把x=16代入3x-15中,求出代数式的值即可.
10.解:(3x-15)元.
当x=16时,原式=3×16-15=33(元).
11.解:如下表:
图形编号 ① ② ③ ④
大三角形周长的火柴棒根数 3 6 9 12
小三角形个数 1 22 32 42
火柴棒根数(选做) 3 3+2×3 3+2×3+3×3 3+2×3+3×3+4×3
(1)3n根.
(2)n2个,第200个图形的小三角形有2002个.
(3).
点拨:(1)显然拼得的三角形都是等边三角形,只需发现边长的规律即可.第n个大三角形的边长是n,周长是3n;(2)只数小三角形的个数,发现:第n个图形中,小三角形的个数是n的平方;(3)第1个图形中需要1×3根,第2个图形中需要1×3+2×3根,以此类推,第n个图形中,需要1×3+2×3+3×3+…+n×3=3(1+2+3+…+n)=(根).
12.解:(1)对原图形进行不同的分割,可得
方法一:
S=bc+d(a-c)
方法二:
S=ad+c(b-d)
方法三:
S=ab-(a-c)(b-d)
(2)S=ab-(a-c)(b-d)=10×12-(10-7)×(12-8)=10×12-3×4=120-12=108.
基础巩固
1.下列式子符合代数式的书写格式的是( ).
A.a·40a B. C.3÷m D.
2.下列说法正确的是( ).
A.单项式m既没有系数,也没有次数 B.单项式5×105的系数是5
C.-2 010也是单项式 D.-3πx2的系数是-3
3.买a台空调花费b元,则买10台这样的空调要花费( ).
A.元 B.10ab元 C.元 D.元
4.多项式2x-3xy2+1是__________次__________项式,其中最高次项是__________,常数项是__________.
5.当x=10,y=9时,代数式x2-y2的值是__________.
6.按照下面的操作步骤,若输入x的值为3,则输出的值为__________.
7.观察一列单项式:a,-2a2,4a3,-8a4,…,根据你发现的规律,第7个单项式为__________;第n个单项式为__________.
8.用代数式表示:
(1)a与b的积的4倍;
(2)x的2倍与y的5%的差;
(3)x的倒数与m除n的商的和;
(4)a与b的差的立方;
(5)a,b两数的立方差(即立方的差);
(6)a与b差的平方的c倍.
能力提升
9.当x=2时,代数式ax3-bx-1的值为1 000,求x=-2时,代数式ax3-bx-1的值.
10.为了节约用水,某市自来水公司采取以下收费方法:每户每月用水不超过10 t,收费1.5元/t;每户每月用水超过10 t,超过的部分按3元/t收费.现在已知小明家2月份用水x t(x>10),请用代数式表示小明家2月份应交水费多少元?如果x=16,那么小明家2月份应交水费多少元?
11.用火柴棒搭图形,填写下表:
图形编号 ① ② ③ ④
大三角形周长的火柴棒根数 3 6
小三角形个数 1
火柴棒根数 3
照这样搭下去,
(1)第n个图形中的大三角形周长的火柴棒是几根?
(2)第n个图形中的小三角形个数有几个?第200个图形中的小三角形个数有几个?
(3)第n个图形需要多少根火柴棒?
12.已知:如图,a=10,b=12,c=7,d=8.
(1)设阴影部分面积为S,用三种不同方法,列出代数式表示S;
(2)以其中一种方法为依据,计算阴影部分面积S.
参考答案
1.B
2.C 解析:只含有字母因式的单项式不能认为它们没有系数,它们的系数是“1”或“-1”;π,5×105,-2 010都是常数.
3.C 解析:买一台空调的花费=总价÷数量,即为元,所以买10台这样的空调要花费为10×=(元).
4.三 三 -3xy2 1 5.19
6.7 解析:实质是求当x=3时,代数式(x-5)2+3的值.
7.64a7 (-2)n-1an
8.(1)4ab;(2)2x-5%y;(3);
(4)(a-b)3;(5)a3-b3;(6)c(a-b)2.
解析:本题解题关键之一是抓住语句中的关键性词语,如:“和、差、倍、倒数、积、商、平方”等,并熟悉它们所对应的每一种运算.第二是分清运算的顺序,一般按先读先写的原则确定其先后顺序.如:(3)x的倒数与m除n的商的和.按题目中叙述的顺序分步如下:①x的倒数即;②m除n的商即;③倒数与商的和即,并要注意除和除以的区别;(4)和(5)两小题要注意二者运算顺序的不同.
9.解:把x=2代入代数式ax3-bx-1中得23a-2b-1=1 000,即8a-2b=1 001;把x=-2代入代数式ax3-bx-1中得-23a+2b-1=-8a+2b-1=-(8a-2b)-1,再把8a-2b=1 001代入得原式=-1 001-1=-1 002.
分析:(1)假设每吨水都是3元,则x t水为3x元,减去前10t水多算的15元,就是小明家2月份应交水费.(2)把x=16代入3x-15中,求出代数式的值即可.
10.解:(3x-15)元.
当x=16时,原式=3×16-15=33(元).
11.解:如下表:
图形编号 ① ② ③ ④
大三角形周长的火柴棒根数 3 6 9 12
小三角形个数 1 22 32 42
火柴棒根数(选做) 3 3+2×3 3+2×3+3×3 3+2×3+3×3+4×3
(1)3n根.
(2)n2个,第200个图形的小三角形有2002个.
(3).
点拨:(1)显然拼得的三角形都是等边三角形,只需发现边长的规律即可.第n个大三角形的边长是n,周长是3n;(2)只数小三角形的个数,发现:第n个图形中,小三角形的个数是n的平方;(3)第1个图形中需要1×3根,第2个图形中需要1×3+2×3根,以此类推,第n个图形中,需要1×3+2×3+3×3+…+n×3=3(1+2+3+…+n)=(根).
12.解:(1)对原图形进行不同的分割,可得
方法一:
S=bc+d(a-c)
方法二:
S=ad+c(b-d)
方法三:
S=ab-(a-c)(b-d)
(2)S=ab-(a-c)(b-d)=10×12-(10-7)×(12-8)=10×12-3×4=120-12=108.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
