京改版八年级数学上册11.1-12.2 三角形的性质课堂提升训练(含解析)
文档属性
| 名称 | 京改版八年级数学上册11.1-12.2 三角形的性质课堂提升训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 434.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 21:50:22 | ||
图片预览



文档简介
2022-2023学年度北京课改版版八年级数学上册
课堂提升训练
第十二章 三角形
一 三角形及其性质
12.1 三角形
12.2 三角形的性质
基础过关全练
知识点1 三角形及其相关概念
图中三角形的个数是( )
A.7 B.6 C.5 D.4
2.如图,在△ABC中,D,E分别是BC,AC上的点,连接BE,AD,BE与AD相交于点F.
(1)图中有几个三角形 请表示出来;
(2)写出△BDF的三个顶点和三条边;
(3)AB是哪些三角形的边
(4)点F是哪些三角形的顶点
知识点2 三角形的稳定性
3.(2022湖北武汉武昌期中)下列图形中,具有稳定性的是( )
A.平行四边形 B.梯形
C.正方形 D.直角三角形
4.(2022独家原创)从斜拉索桥、起重机吊臂、篮球架、自行车架中可以发现三角形结构,这主要是利用了 .
知识点3 三角形边的性质
5.(2022北京顺义期末)在下列长度的四个线段中,能与长为3 cm,9 cm的两个线段首尾顺次相接组成一个三角形的是( )
A.3 cm B.6 cm
C.10 cm D.12 cm
6.(2022独家原创)若一个等腰三角形的三边长分别为5 cm,10 cm,a cm,则它的周长为( )
A.20 cm B.25 cm
C.15 cm D.20 cm或25 cm
7.(2021江苏淮安中考)一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是 .
8.(2021黑龙江大庆中考改编)三个数3,1-a,1-2a所对应的点在数轴上从左到右依次排列,若长为3,1-a,1-2a的三条线段能构成三角形,则a的取值范围为 .
9.(2021北京海淀期中)若三角形的三边长分别为a、b、c,则|a+b-c|-|a-b-c|= .
10.一个等腰三角形的周长为20 cm,其一边长为6 cm,求其他两边的长.
11.如图所示,D是△ABC的边AC上任意一点(不含端点),连接BD,请判断AB+BC+AC与2BD的大小关系,并说明理由.
知识点4 三角形角的性质
12. 如图是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,则这块三角形木板缺少的角的度数为( )
A.30° B.40° C.50° D.60°
13.(2021广西河池中考)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的度数为( )
A.90° B.80° C.60° D.40°
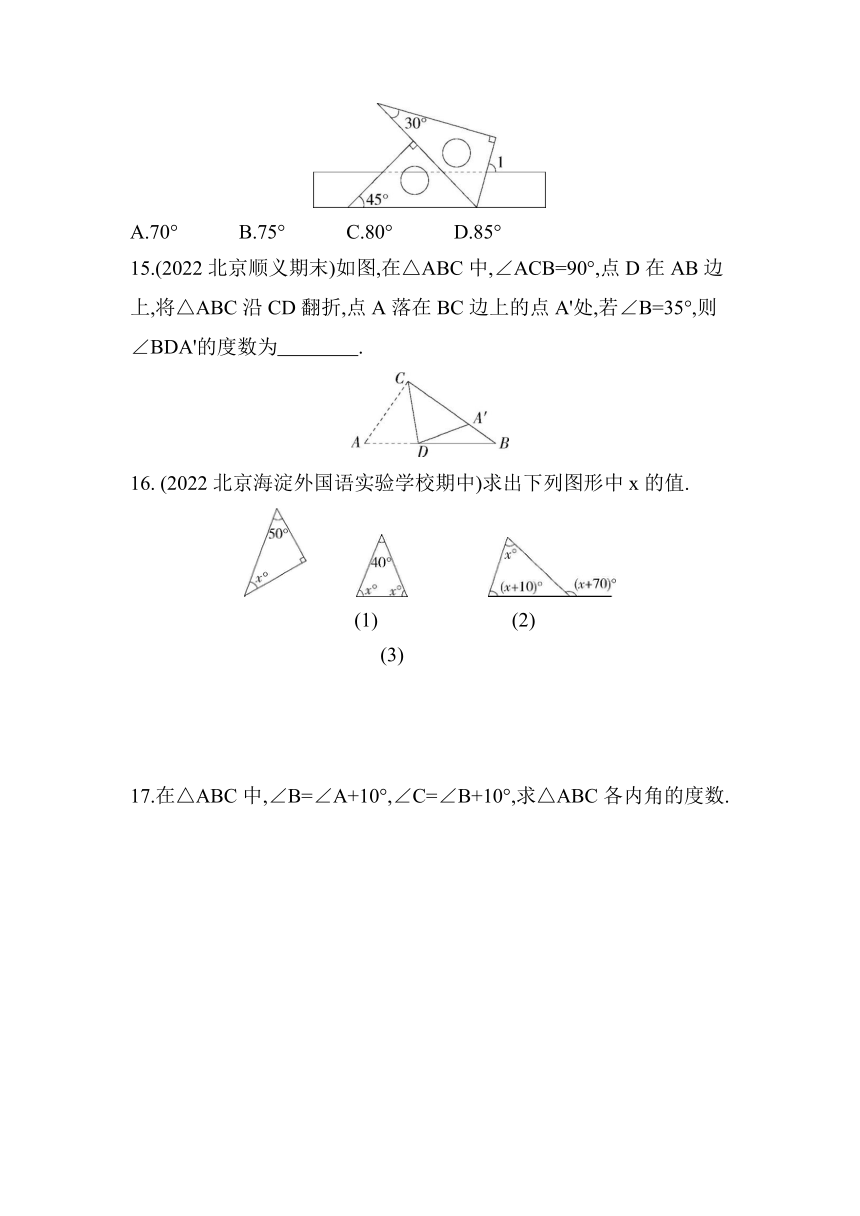
14.(2021贵州毕节中考)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
15.(2022北京顺义期末)如图,在△ABC中,∠ACB=90°,点D在AB边上,将△ABC沿CD翻折,点A落在BC边上的点A'处,若∠B=35°,则∠BDA'的度数为 .
16. (2022北京海淀外国语实验学校期中)求出下列图形中x的值.
(2) (3)
17.在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.
18.△ABC中,∠C=80°,点D、E分别是△ABC边AC、BC上的点,点P是边AB上的一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)如图1,若∠α=50°,则∠1+∠2= ;
(2)如图2,猜想∠α、∠1、∠2之间的数量关系,并证明.
图1 图2
知识点5 三角形按角分类
19.(2022独家原创)“窥一斑而知全豹”出自刘义庆《世说新语·方正》.现在,多用此句形容通过局部了解全部.下面给出的四个三角形都被遮挡了一部分,其中不能判断三角形的类型的是 ( )
A B C D
20.在△ABC中,∠A=∠B=∠C,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
能力提升全练
21. 下列图形具有稳定性的是( )
A B C D
22. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )
A.1 B.2 C.4 D.8
23. 在△ABC中,∠A=20°,∠B=4∠C,则∠C的度数为( )
A.32° B.36° C.40° D.128°
24. 将一副三角板按如图方式重叠摆放,则∠1的度数为( )
A.45° B.60° C.75° D.105°
25.(2022北京东城期末,6,)如图,BD平分∠ABC,DE∥BC,交AB于点E.若∠A=30°,∠BDC=50°,则∠BDE的度数是( )
A.10° B.20°
C.30° D.50°
26. )已知n是正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有( )
A.4个 B.5个 C.6个 D.7个
27. 如图,在△ABC中,点D、E分别在BC、AC上,∠B=40°,
∠C=60°,若DE∥AB,则∠AED= °.
28. 已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c= .
29.(2022浙江杭州钱江新城实验学校,12,)等腰三角形的周长为24 cm,其中一边长为7 cm,则另外两条边的长为 .
30.(2022北京陈经纶中学,20,)如图,点D为△ABC的边BC的延长线上的一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=40°,求∠ACD的度数.
31.(2022北京海淀外国语实验学校期中,24,)若三边均不相等的三角形三边长分别为a、b、c,且满足a-b>b-c(a为最长边的长,c为最短边的长),则称这个三角形为“不均衡三角形”.例如,一个三角形三边长分别为7,5,4,因为7-5>5-4,所以这个三角形为“不均衡三角形”.
(1)有以下4组长度的线段,其中能组成“不均衡三角形”的为 (填序号).
①4 cm,2 cm,1 cm;
②13 cm,18 cm,9 cm;
③19 cm,20 cm,19 cm;
④9 cm,8 cm,6 cm.
(2)已知“不均衡三角形”的三边长分别为2x+2,16,2x-6,则整数x的值为 .
素养探究全练
32.[逻辑推理]在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如图,△ABC中,∠ACB=90°,点P是线段AB上一点(不与A、B重合),连接CP.
(1)当∠B=72°时,
①若∠CPB=54°,则△ACP “倍角三角形”(填“是”或“不是”).
②若△BPC是“倍角三角形”,求∠ACP的度数.
(2)当△ABC、△BPC、△ACP都是“倍角三角形”时,求∠BCP的度数.
备用图1 备用图2
答案全解全析
基础过关全练
1.B 题图中的三角形分别为△ABD,△ADE,△ACE,△ABE,△ACD,△ABC,共6个.
2.解析 (1)题图中共有8个三角形,分别是△BDF,△BEC,△BDA,△BFA,△AEF,△AEB,△ADC,△ABC.
(2)△BDF的三个顶点分别是B,D,F,三条边分别是BD,DF,BF.
(3)AB是△ABF,△ABD,△ABE,△ABC的边.
(4)点F是△BDF,△ABF,△AEF的顶点.
3.D 根据三角形具有稳定性,可知四个选项中直角三角形具有稳定性.故选D.
4.三角形的稳定性
解析 题中的物体都有三角形结构,主要是利用三角形的稳定性.
5.C 设能与长为3 cm,9 cm的两个线段组成三角形的线段的长为c cm,则9-36.B 若5 cm长的边为底边,则10 cm长的边为腰,此时a=10,周长为25 cm;若5 cm长的边为腰,则10 cm长的边为底边,此时a=5,因为5+5=10不符合三角形两边之和大于第三边,所以a=5不符合题意,舍去.综上,这个等腰三角形的周长为25 cm.
7.4
解析 设第三边的长为a,根据三角形的三边关系知,4-18.-3解析 由这三个数的大小关系初步确定a的取值范围为a<-2,再由三角形的三边关系得到3+(1-a)>1-2a,解得a>-3,∴a的取值范围为-39.2a-2c
解析 ∵三角形的三边长分别为a、b、c,
∴a+b>c,a-b0,a-b-c<0,
∴|a+b-c|-|a-b-c|=a+b-c+(a-b-c)
=a+b-c+a-b-c=2a-2c.
10.解析 分两种情况讨论:
(1)当底边长为6 cm时,腰长为(20-6)÷2=7(cm),此时三边长分别为6 cm,7 cm,7 cm,可以构成三角形.
(2)当腰长为6 cm时,底边长为20-6×2=8(cm),此时三边长分别为6 cm,6 cm,8 cm,可以构成三角形.
综上,其他两边的长分别为7 cm,7 cm或6 cm,8 cm.
11.解析 AB+BC+AC>2BD.理由:
在△ABD中,AB+AD>BD,在△BCD中,BC+CD>BD,
∴AB+AD+BC+CD>2BD,
∴AB+BC+AC>2BD.
12.B 根据三角形内角和定理可知,缺少的角的度数为180°-110°-30°=40°.
13.B 由三角形内角和定理推论得,∠C=∠CBD-∠A=120°-40°=80°.
14.B 如图,
易知∠2=180°-90°-30°=60°,∠4=180°-45°-90°=45°,∴∠3=180°-45°-60°=75°,
∵a∥b,∴∠1=∠3=75°,故选B.
15.20°
解析 ∵∠ACB=90°,∴∠A+∠B=90°,
∵△CDA'是由△CDA翻折得到的,∴∠CA'D=∠A,
∵∠CA'D=∠B+∠BDA'=35°+∠BDA',
∴35°+∠BDA'+35°=90°,∴∠BDA'=20°.
16.解析 (1)x=180-90-50=40.
(2)∵x+x+40=180,∴x=70.
(3)∵x+70=x+x+10,∴x=60.
17.解析 设∠A=x°(x>0),
则∠B=(x+10)°,∠C=(x+20)°,
故可列方程为x+(x+10)+(x+20)=180,解得x=50,
∴∠A=50°,∠B=60°,∠C=70°.
18.解析 (1)如图1,连接CP,
∵∠1是△CDP的外角,∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+50°=130°.
图1
(2)如图2,连接CP,
∵∠1是△CDP的外角,∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+∠α.
图2
19.C A项,根据露出的两个角,可判断这个三角形是锐角三角形;B项,露出的角是直角,因此这个三角形是直角三角形;C项,露出的角是锐角,其他两个角的大小无法确定,因此不能判断出三角形的类型;D项,露出的角是钝角,因此这个三角形是钝角三角形.故选C.
20.B 由∠A=∠B=∠C,得∠B=2∠A,∠C=3∠A,代入∠A+∠B+∠C=180°,得∠A+2∠A+3∠A=180°,解得∠A=30°,所以∠B=60°,∠C=90°,所以△ABC是直角三角形.
能力提升全练
21.A 三角形具有稳定性.故选A.
22.C 由三角形的三边关系,得5-323.A 由三角形内角和定理可知:∠A+∠B+∠C=180°,∵∠A=20°,∠B=4∠C,∴20°+4∠C+∠C=180°,解得∠C=32°.故选A.
24.C 如图,由题可知∠DBC=30°,∠ACB=45°,∴∠1=30°+45°=75°.故选C.
25.B ∵BD平分∠ABC,∴∠ABD=∠CBD.
∵DE∥BC,∴∠BDE=∠CBD,∴∠ABD=∠BDE.
∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=50°,
∴50°=30°+∠ABD,∴∠ABD=20°.∴∠BDE=20°.
26.D n+2,n+8,3n中最大的可能为n+8,也可能为3n,故分两种情况讨论:①当n+8>3n,即n<4时,(n+2)+3n>n+8,解得n>2,∴23n,解得n<10,∴4≤n<10,故满足条件的n的值为4,5,6,7,8,9,共6个.
综上所述,满足条件的n的值有7个.
27.100
解析 在△ABC中,∠A+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠A=180°-∠B-∠C=180°-40°-60°=80°,
∵DE∥AB,∴∠A+∠AED=180°,
∴∠AED=180°-80°=100°.
28.7
解析 ∵a,b满足|a-7|+(b-1)2=0,∴a-7=0,b-1=0,解得a=7,b=1,∵7-1=6,7+1=8,∴629.8.5 cm、8.5 cm或7 cm、10 cm
解析 ∵等腰三角形的周长是24 cm,一条边长是7 cm,∴当7 cm长的边为底边时,其他两边长都为(24-7)÷2=8.5(cm),此时三角形的三边长分别为7 cm、8.5 cm、8.5 cm,可以构成三角形;当7 cm长的边为腰时,其他两边长为7 cm和10 cm,此时三角形的三边长分别为7 cm、7 cm、10 cm,可以构成三角形.∴另外两条边的长为8.5 cm、8.5 cm或7 cm、10 cm.
30.解析 ∵DF⊥AB,∴∠AFD=90°.
∵∠AFD=∠B+∠D,
∴∠B=∠AFD-∠D=90°-40°=50°.
∴∠ACD=∠B+∠A=50°+35°=85°.
31.解析 (1)①∵1+2<4,∴4 cm,2 cm,1 cm长的线段不能组成“不均衡三角形”.
②∵18-13>13-9,∴13 cm,18 cm,9 cm长的线段能组成“不均衡三角形”.
③∵19=19,∴19 cm,20 cm,19 cm长的线段不能组成“不均衡三角形”.
④∵9-8<8-6,∴9 cm,8 cm,6 cm长的线段不能组成“不均衡三角形”.
故答案为②.
(2)由题可知,2x+2,16,2x-6都为正数,且互不相等,其中最大数可能为2x+2,也可能为16,分情况进行讨论:①当16>2x+2,即x<7时,16-(2x+2)>2x+2-(2x-6),解得x<3,
此时2x-6<0,不合题意,舍去.
②当2x+2>16,即x>7时,若16>2x-6,则x<11,
2x+2-16>16-(2x-6),解得x>9,
∴9当x=10时,三边长分别为22,16,14,可构成三角形,符合题意;若2x-6>16,则x>11,
2x+2-(2x-6)>2x-6-16,解得x<15,
∴11当x=12时,三边长分别为26,16,18,可构成三角形;当x=13时,三边长分别为28,16,20,可构成三角形;当x=14时,三边长分别为30,16,22,可构成三角形,故x=12,13,14符合题意.
综上所述,整数x的值为10,12,13,14.
素养探究全练
32.解析 (1)①是.
②∵∠B=72°,△BPC是“倍角三角形”,
∴△BCP的三个内角的度数分别是72°,72°,36°,
∴∠BCP=36°或72°,
∵∠ACB=90°,∴∠ACP=54°或18°.
(2)∵∠ACB=90°,且△ABC为“倍角三角形”,
∴从△ABC入手进行分类讨论:
①当∠ACB=2∠A时,易知∠A=∠B=45°,
若CP⊥AB,则∠CPB=∠CPA=90°,如图1,易知∠BCP=45°,∠ACP=45°,此时△BCP与△ACP都是“倍角三角形”.
②当∠A=2∠B时,易知∠A=60°,∠B=30°,
若∠BCP=2∠B,则∠BCP=60°,如图2,易知∠ACP=30°,∠BPC=∠APC=90°,此时△BCP与△ACP都是“倍角三角形”;
若∠BPC=2∠BCP,则∠BCP=50°,∠BPC=100°,如图3,易知∠ACP=40°,∠APC=80°,此时△BCP与△ACP都是“倍角三角形”.
③当∠B=2∠A时,易知∠A=30°,∠B=60°,
若∠B=2∠BCP,则∠BCP=30°,如图4,易知∠BPC=90°,∠APC=90°,∠ACP=60°,此时△BCP与△ACP都是“倍角三角形”;
若∠BPC=2∠BCP,则∠BCP=40°,∠BPC=80°,如图5,易知∠APC=100°,∠ACP=50°,此时△BCP与△ACP都是“倍角三角形”.
综上,满足条件的∠BCP的度数为30°,40°,45°,50°,60°.
图 1 图2 图3 图4 图5
课堂提升训练
第十二章 三角形
一 三角形及其性质
12.1 三角形
12.2 三角形的性质
基础过关全练
知识点1 三角形及其相关概念
图中三角形的个数是( )
A.7 B.6 C.5 D.4
2.如图,在△ABC中,D,E分别是BC,AC上的点,连接BE,AD,BE与AD相交于点F.
(1)图中有几个三角形 请表示出来;
(2)写出△BDF的三个顶点和三条边;
(3)AB是哪些三角形的边
(4)点F是哪些三角形的顶点
知识点2 三角形的稳定性
3.(2022湖北武汉武昌期中)下列图形中,具有稳定性的是( )
A.平行四边形 B.梯形
C.正方形 D.直角三角形
4.(2022独家原创)从斜拉索桥、起重机吊臂、篮球架、自行车架中可以发现三角形结构,这主要是利用了 .
知识点3 三角形边的性质
5.(2022北京顺义期末)在下列长度的四个线段中,能与长为3 cm,9 cm的两个线段首尾顺次相接组成一个三角形的是( )
A.3 cm B.6 cm
C.10 cm D.12 cm
6.(2022独家原创)若一个等腰三角形的三边长分别为5 cm,10 cm,a cm,则它的周长为( )
A.20 cm B.25 cm
C.15 cm D.20 cm或25 cm
7.(2021江苏淮安中考)一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是 .
8.(2021黑龙江大庆中考改编)三个数3,1-a,1-2a所对应的点在数轴上从左到右依次排列,若长为3,1-a,1-2a的三条线段能构成三角形,则a的取值范围为 .
9.(2021北京海淀期中)若三角形的三边长分别为a、b、c,则|a+b-c|-|a-b-c|= .
10.一个等腰三角形的周长为20 cm,其一边长为6 cm,求其他两边的长.
11.如图所示,D是△ABC的边AC上任意一点(不含端点),连接BD,请判断AB+BC+AC与2BD的大小关系,并说明理由.
知识点4 三角形角的性质
12. 如图是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,则这块三角形木板缺少的角的度数为( )
A.30° B.40° C.50° D.60°
13.(2021广西河池中考)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的度数为( )
A.90° B.80° C.60° D.40°
14.(2021贵州毕节中考)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
15.(2022北京顺义期末)如图,在△ABC中,∠ACB=90°,点D在AB边上,将△ABC沿CD翻折,点A落在BC边上的点A'处,若∠B=35°,则∠BDA'的度数为 .
16. (2022北京海淀外国语实验学校期中)求出下列图形中x的值.
(2) (3)
17.在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.
18.△ABC中,∠C=80°,点D、E分别是△ABC边AC、BC上的点,点P是边AB上的一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)如图1,若∠α=50°,则∠1+∠2= ;
(2)如图2,猜想∠α、∠1、∠2之间的数量关系,并证明.
图1 图2
知识点5 三角形按角分类
19.(2022独家原创)“窥一斑而知全豹”出自刘义庆《世说新语·方正》.现在,多用此句形容通过局部了解全部.下面给出的四个三角形都被遮挡了一部分,其中不能判断三角形的类型的是 ( )
A B C D
20.在△ABC中,∠A=∠B=∠C,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
能力提升全练
21. 下列图形具有稳定性的是( )
A B C D
22. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )
A.1 B.2 C.4 D.8
23. 在△ABC中,∠A=20°,∠B=4∠C,则∠C的度数为( )
A.32° B.36° C.40° D.128°
24. 将一副三角板按如图方式重叠摆放,则∠1的度数为( )
A.45° B.60° C.75° D.105°
25.(2022北京东城期末,6,)如图,BD平分∠ABC,DE∥BC,交AB于点E.若∠A=30°,∠BDC=50°,则∠BDE的度数是( )
A.10° B.20°
C.30° D.50°
26. )已知n是正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有( )
A.4个 B.5个 C.6个 D.7个
27. 如图,在△ABC中,点D、E分别在BC、AC上,∠B=40°,
∠C=60°,若DE∥AB,则∠AED= °.
28. 已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c= .
29.(2022浙江杭州钱江新城实验学校,12,)等腰三角形的周长为24 cm,其中一边长为7 cm,则另外两条边的长为 .
30.(2022北京陈经纶中学,20,)如图,点D为△ABC的边BC的延长线上的一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=40°,求∠ACD的度数.
31.(2022北京海淀外国语实验学校期中,24,)若三边均不相等的三角形三边长分别为a、b、c,且满足a-b>b-c(a为最长边的长,c为最短边的长),则称这个三角形为“不均衡三角形”.例如,一个三角形三边长分别为7,5,4,因为7-5>5-4,所以这个三角形为“不均衡三角形”.
(1)有以下4组长度的线段,其中能组成“不均衡三角形”的为 (填序号).
①4 cm,2 cm,1 cm;
②13 cm,18 cm,9 cm;
③19 cm,20 cm,19 cm;
④9 cm,8 cm,6 cm.
(2)已知“不均衡三角形”的三边长分别为2x+2,16,2x-6,则整数x的值为 .
素养探究全练
32.[逻辑推理]在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如图,△ABC中,∠ACB=90°,点P是线段AB上一点(不与A、B重合),连接CP.
(1)当∠B=72°时,
①若∠CPB=54°,则△ACP “倍角三角形”(填“是”或“不是”).
②若△BPC是“倍角三角形”,求∠ACP的度数.
(2)当△ABC、△BPC、△ACP都是“倍角三角形”时,求∠BCP的度数.
备用图1 备用图2
答案全解全析
基础过关全练
1.B 题图中的三角形分别为△ABD,△ADE,△ACE,△ABE,△ACD,△ABC,共6个.
2.解析 (1)题图中共有8个三角形,分别是△BDF,△BEC,△BDA,△BFA,△AEF,△AEB,△ADC,△ABC.
(2)△BDF的三个顶点分别是B,D,F,三条边分别是BD,DF,BF.
(3)AB是△ABF,△ABD,△ABE,△ABC的边.
(4)点F是△BDF,△ABF,△AEF的顶点.
3.D 根据三角形具有稳定性,可知四个选项中直角三角形具有稳定性.故选D.
4.三角形的稳定性
解析 题中的物体都有三角形结构,主要是利用三角形的稳定性.
5.C 设能与长为3 cm,9 cm的两个线段组成三角形的线段的长为c cm,则9-3
7.4
解析 设第三边的长为a,根据三角形的三边关系知,4-1
解析 ∵三角形的三边长分别为a、b、c,
∴a+b>c,a-b
∴|a+b-c|-|a-b-c|=a+b-c+(a-b-c)
=a+b-c+a-b-c=2a-2c.
10.解析 分两种情况讨论:
(1)当底边长为6 cm时,腰长为(20-6)÷2=7(cm),此时三边长分别为6 cm,7 cm,7 cm,可以构成三角形.
(2)当腰长为6 cm时,底边长为20-6×2=8(cm),此时三边长分别为6 cm,6 cm,8 cm,可以构成三角形.
综上,其他两边的长分别为7 cm,7 cm或6 cm,8 cm.
11.解析 AB+BC+AC>2BD.理由:
在△ABD中,AB+AD>BD,在△BCD中,BC+CD>BD,
∴AB+AD+BC+CD>2BD,
∴AB+BC+AC>2BD.
12.B 根据三角形内角和定理可知,缺少的角的度数为180°-110°-30°=40°.
13.B 由三角形内角和定理推论得,∠C=∠CBD-∠A=120°-40°=80°.
14.B 如图,
易知∠2=180°-90°-30°=60°,∠4=180°-45°-90°=45°,∴∠3=180°-45°-60°=75°,
∵a∥b,∴∠1=∠3=75°,故选B.
15.20°
解析 ∵∠ACB=90°,∴∠A+∠B=90°,
∵△CDA'是由△CDA翻折得到的,∴∠CA'D=∠A,
∵∠CA'D=∠B+∠BDA'=35°+∠BDA',
∴35°+∠BDA'+35°=90°,∴∠BDA'=20°.
16.解析 (1)x=180-90-50=40.
(2)∵x+x+40=180,∴x=70.
(3)∵x+70=x+x+10,∴x=60.
17.解析 设∠A=x°(x>0),
则∠B=(x+10)°,∠C=(x+20)°,
故可列方程为x+(x+10)+(x+20)=180,解得x=50,
∴∠A=50°,∠B=60°,∠C=70°.
18.解析 (1)如图1,连接CP,
∵∠1是△CDP的外角,∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+50°=130°.
图1
(2)如图2,连接CP,
∵∠1是△CDP的外角,∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+∠α.
图2
19.C A项,根据露出的两个角,可判断这个三角形是锐角三角形;B项,露出的角是直角,因此这个三角形是直角三角形;C项,露出的角是锐角,其他两个角的大小无法确定,因此不能判断出三角形的类型;D项,露出的角是钝角,因此这个三角形是钝角三角形.故选C.
20.B 由∠A=∠B=∠C,得∠B=2∠A,∠C=3∠A,代入∠A+∠B+∠C=180°,得∠A+2∠A+3∠A=180°,解得∠A=30°,所以∠B=60°,∠C=90°,所以△ABC是直角三角形.
能力提升全练
21.A 三角形具有稳定性.故选A.
22.C 由三角形的三边关系,得5-3
24.C 如图,由题可知∠DBC=30°,∠ACB=45°,∴∠1=30°+45°=75°.故选C.
25.B ∵BD平分∠ABC,∴∠ABD=∠CBD.
∵DE∥BC,∴∠BDE=∠CBD,∴∠ABD=∠BDE.
∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=50°,
∴50°=30°+∠ABD,∴∠ABD=20°.∴∠BDE=20°.
26.D n+2,n+8,3n中最大的可能为n+8,也可能为3n,故分两种情况讨论:①当n+8>3n,即n<4时,(n+2)+3n>n+8,解得n>2,∴2
综上所述,满足条件的n的值有7个.
27.100
解析 在△ABC中,∠A+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠A=180°-∠B-∠C=180°-40°-60°=80°,
∵DE∥AB,∴∠A+∠AED=180°,
∴∠AED=180°-80°=100°.
28.7
解析 ∵a,b满足|a-7|+(b-1)2=0,∴a-7=0,b-1=0,解得a=7,b=1,∵7-1=6,7+1=8,∴6
解析 ∵等腰三角形的周长是24 cm,一条边长是7 cm,∴当7 cm长的边为底边时,其他两边长都为(24-7)÷2=8.5(cm),此时三角形的三边长分别为7 cm、8.5 cm、8.5 cm,可以构成三角形;当7 cm长的边为腰时,其他两边长为7 cm和10 cm,此时三角形的三边长分别为7 cm、7 cm、10 cm,可以构成三角形.∴另外两条边的长为8.5 cm、8.5 cm或7 cm、10 cm.
30.解析 ∵DF⊥AB,∴∠AFD=90°.
∵∠AFD=∠B+∠D,
∴∠B=∠AFD-∠D=90°-40°=50°.
∴∠ACD=∠B+∠A=50°+35°=85°.
31.解析 (1)①∵1+2<4,∴4 cm,2 cm,1 cm长的线段不能组成“不均衡三角形”.
②∵18-13>13-9,∴13 cm,18 cm,9 cm长的线段能组成“不均衡三角形”.
③∵19=19,∴19 cm,20 cm,19 cm长的线段不能组成“不均衡三角形”.
④∵9-8<8-6,∴9 cm,8 cm,6 cm长的线段不能组成“不均衡三角形”.
故答案为②.
(2)由题可知,2x+2,16,2x-6都为正数,且互不相等,其中最大数可能为2x+2,也可能为16,分情况进行讨论:①当16>2x+2,即x<7时,16-(2x+2)>2x+2-(2x-6),解得x<3,
此时2x-6<0,不合题意,舍去.
②当2x+2>16,即x>7时,若16>2x-6,则x<11,
2x+2-16>16-(2x-6),解得x>9,
∴9
2x+2-(2x-6)>2x-6-16,解得x<15,
∴11
综上所述,整数x的值为10,12,13,14.
素养探究全练
32.解析 (1)①是.
②∵∠B=72°,△BPC是“倍角三角形”,
∴△BCP的三个内角的度数分别是72°,72°,36°,
∴∠BCP=36°或72°,
∵∠ACB=90°,∴∠ACP=54°或18°.
(2)∵∠ACB=90°,且△ABC为“倍角三角形”,
∴从△ABC入手进行分类讨论:
①当∠ACB=2∠A时,易知∠A=∠B=45°,
若CP⊥AB,则∠CPB=∠CPA=90°,如图1,易知∠BCP=45°,∠ACP=45°,此时△BCP与△ACP都是“倍角三角形”.
②当∠A=2∠B时,易知∠A=60°,∠B=30°,
若∠BCP=2∠B,则∠BCP=60°,如图2,易知∠ACP=30°,∠BPC=∠APC=90°,此时△BCP与△ACP都是“倍角三角形”;
若∠BPC=2∠BCP,则∠BCP=50°,∠BPC=100°,如图3,易知∠ACP=40°,∠APC=80°,此时△BCP与△ACP都是“倍角三角形”.
③当∠B=2∠A时,易知∠A=30°,∠B=60°,
若∠B=2∠BCP,则∠BCP=30°,如图4,易知∠BPC=90°,∠APC=90°,∠ACP=60°,此时△BCP与△ACP都是“倍角三角形”;
若∠BPC=2∠BCP,则∠BCP=40°,∠BPC=80°,如图5,易知∠APC=100°,∠ACP=50°,此时△BCP与△ACP都是“倍角三角形”.
综上,满足条件的∠BCP的度数为30°,40°,45°,50°,60°.
图 1 图2 图3 图4 图5
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
