人教版数学八年级上册 11.2.1三角形的内角 课件(共14张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.2.1三角形的内角 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 944.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 18:59:40 | ||
图片预览




文档简介
(共19张PPT)
11.2.1三角形的内角
三角形的三个内角和是多少
三角形的三个内角和是多少
三角形内角和定理:
三角形三个内角的和等于180°
自学课本12至13页例2,思考:
1、课本第12-13页例2你看懂了吗?
2、还有其他解法吗?
3、完成第13页练习1。
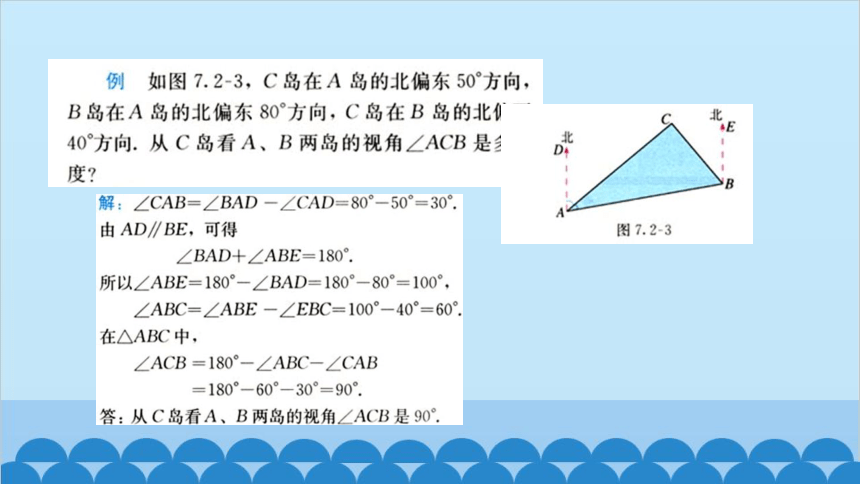
B
D
C
E
北
A
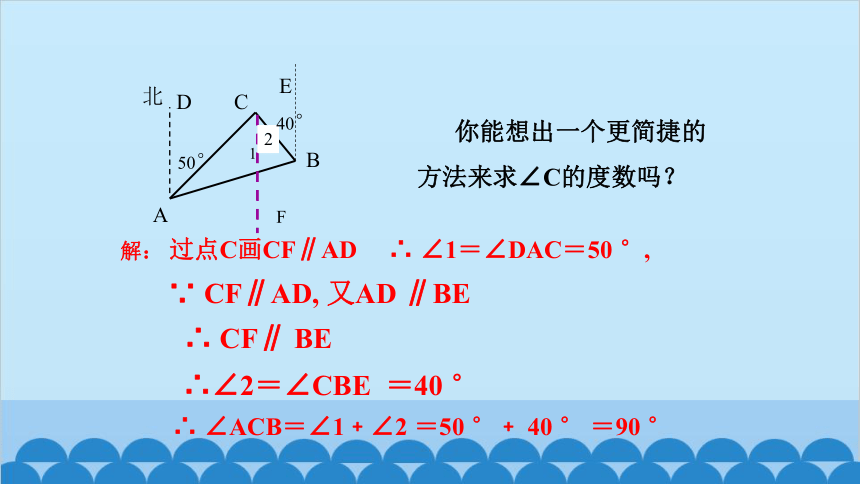
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °,
F
∵ CF∥AD, 又AD ∥BE
∴ CF∥ BE
∴∠2=∠CBE =40 °
∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °
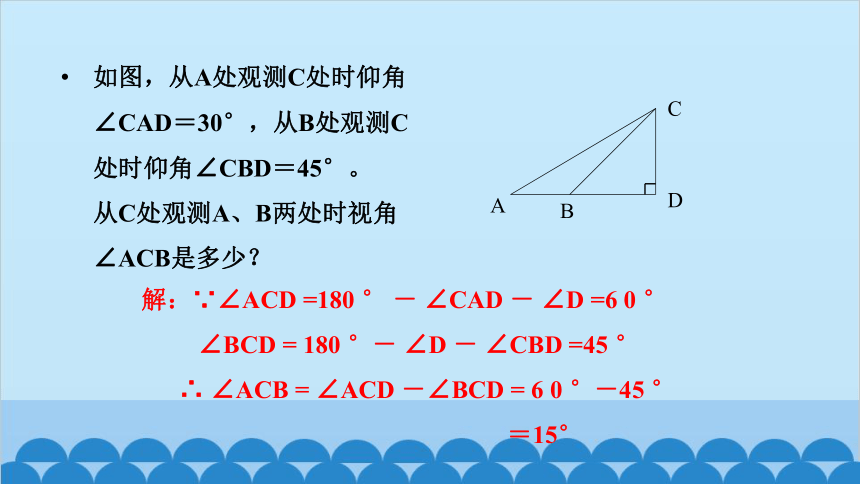
如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。 从C处观测A、B两处时视角 ∠ACB是多少?
A
B
C
D
解:∵∠ACD =180 ° - ∠CAD - ∠D =6 0 °
∠BCD = 180 °- ∠D - ∠CBD =45 °
∴ ∠ACB = ∠ACD -∠BCD = 6 0 °-45 °
=15°
自学课本13-14页例3,思考:
1、直角三角形的两个锐角有什么关系?你会用几何语言表达吗?
2、 14页例3你理解吗?
3、完成第14页思考。
直角三角形的两个锐角 。
A
C
B
几何语言:
∵在Rt△ABC中∠C=90°
∴ ∠ + =90°
互余
A B
有两个角 的三角形是直角三角形。
A
C
B
∴△ABC是 。
几何语言:
∵ ∠ + =90°
互余
A B
直角三角形
1.如图∠ABC=90°,CD⊥AB ,垂足为D ,∠ACD 与 ∠B有什么关系?为什么?
2.如图∠C=90°,∠1 = ∠2,△ADE是直角三角形吗?为什么?
小结归纳
小结归纳
1、本节课你学到了哪些知识?
2、你还有什么疑问?
如图a∥b, ∠1+ ∠2=75°, 求∠3+ ∠4 的度数。
作业布置
A组作业:课本第17页8、9、10题
练习册第4页10、11题
B组作业:课本第17页8、9、10题
练习册第4页10、11题
11.2.1三角形的内角
三角形的三个内角和是多少
三角形的三个内角和是多少
三角形内角和定理:
三角形三个内角的和等于180°
自学课本12至13页例2,思考:
1、课本第12-13页例2你看懂了吗?
2、还有其他解法吗?
3、完成第13页练习1。
B
D
C
E
北
A
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °,
F
∵ CF∥AD, 又AD ∥BE
∴ CF∥ BE
∴∠2=∠CBE =40 °
∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °
如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。 从C处观测A、B两处时视角 ∠ACB是多少?
A
B
C
D
解:∵∠ACD =180 ° - ∠CAD - ∠D =6 0 °
∠BCD = 180 °- ∠D - ∠CBD =45 °
∴ ∠ACB = ∠ACD -∠BCD = 6 0 °-45 °
=15°
自学课本13-14页例3,思考:
1、直角三角形的两个锐角有什么关系?你会用几何语言表达吗?
2、 14页例3你理解吗?
3、完成第14页思考。
直角三角形的两个锐角 。
A
C
B
几何语言:
∵在Rt△ABC中∠C=90°
∴ ∠ + =90°
互余
A B
有两个角 的三角形是直角三角形。
A
C
B
∴△ABC是 。
几何语言:
∵ ∠ + =90°
互余
A B
直角三角形
1.如图∠ABC=90°,CD⊥AB ,垂足为D ,∠ACD 与 ∠B有什么关系?为什么?
2.如图∠C=90°,∠1 = ∠2,△ADE是直角三角形吗?为什么?
小结归纳
小结归纳
1、本节课你学到了哪些知识?
2、你还有什么疑问?
如图a∥b, ∠1+ ∠2=75°, 求∠3+ ∠4 的度数。
作业布置
A组作业:课本第17页8、9、10题
练习册第4页10、11题
B组作业:课本第17页8、9、10题
练习册第4页10、11题
