第二十三章 旋转单元质量检测试卷A(含解析)
文档属性
| 名称 | 第二十三章 旋转单元质量检测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 20:15:34 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2022-20203学年九年级(上)第二十三章旋转检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 下列四边形中,是中心对称但不是轴对称的图形是
A. 矩形 B. 等腰梯形 C. 正方形 D. 平行四边形
2. 下列图形中,是中心对称图形,但不是轴对称图形的是
A. 等腰三角形 B. 平行四边形 C. 长方形 D. 五边形
3. 年冬季奥运会将在北京和张家口举行,如图所示的滑雪人经过旋转不能得到的是
A. B.
C. D.
4. 如图所示,在平面直角坐标系中,,, 是等腰直角三角形且 ,把 绕点 顺时针旋转 ,得到 ,把 绕点 顺时针旋转 ,得到 ,依此类推,得到的等腰直角三角形的直角顶点 的坐标为
A. B. C. D.
5. 下列图形中是中心对称图形,但不是轴对称图形的是
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
6. 将 绕点 旋转 得到 ,则下列作图正确的是
A. B.
C. D.
7. 一副三角板 、 ,如图 放置( 、 ),将三角板 绕点 逆时针旋转一定角度,如图 所示,且 ,则下列结论中正确的是
① 的角度恒为 ;
②在旋转过程中,若 平分 , 平分 , 的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成 的次数为 次;
④在图 的情况下,作 ,则 平分 .
A. ① B. ② C. ①②④ D. ①②③④
8. 如图,在等边三角形 中,在 边上取两点 ,,使 .若 ,,,则以 ,, 为边长的三角形的形状为
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随 ,, 的值而定
9. 已知图中所有的小正方形都全等,若在右侧添加一个全等的小正方形,使得到的新图形是中心对称图形,则正确的添加方案是
A. B.
C. D.
10. 线段 以点 为旋转中心,逆时针旋转 ,得到 ,再将 以点 为旋转中心逆时针旋转 得到 ,依此操作直到点 与点 重合为止,顺次连接点 , 形成的多边形是
A. 正四边形 B. 正五边形 C. 正六边形 D. 正七边形
二、填空题(共6小题;每小题3分,共18分)
11. 若两个图形成中心对称,分别联结这两个图形的两对对应点,所得两条直线的交点就是 .
12. 平面内,一个图形绕着一个定点旋转 后,能与另一个图形重合,叫做这两个图形 ,也叫做这两个图形 ,这个定点叫做 ,这两个图形中的对应点,也叫做关于这个定点的 .
13. 如果一个图形绕着所在平面内的一个定点旋转 后,能与原图形重合,那么这个图形叫做 ,这个定点叫做 .
14. 已知点 关于原点对称的点为 ,点 关于 轴对称的点为 ,点 在第四象限,那么 的取值范围是 .
15. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
16. 如图,已知在 中,,,将 绕点 逆时针旋转 后得 ,点 落在点 处,点 落在点 处,连接 ,,作 的平分线 ,交线段 于点 ,交线段 于点 ,那么 的值为 .
三、解答题(共9小题;共72分)
17. (8分)如图,下面两个图案都是由 个大小一样的小长方形拼成的,并且图()中央小正方形的边长是 厘米.问:
(1)图案()、图案()是中心对称图形吗
图() ;图() .(填:“是”或“不是”)
(2)求小长方形的长和宽.
18. (8分)为了美化环境,需要在一块正方形空地上分别种植四种不同的花草,现将这块空地按下列要求分成 块:(画出 种方法)
()分割后整个图形必须是中心对称图形;
() 块图形形状相同;
() 块图形面积相等.
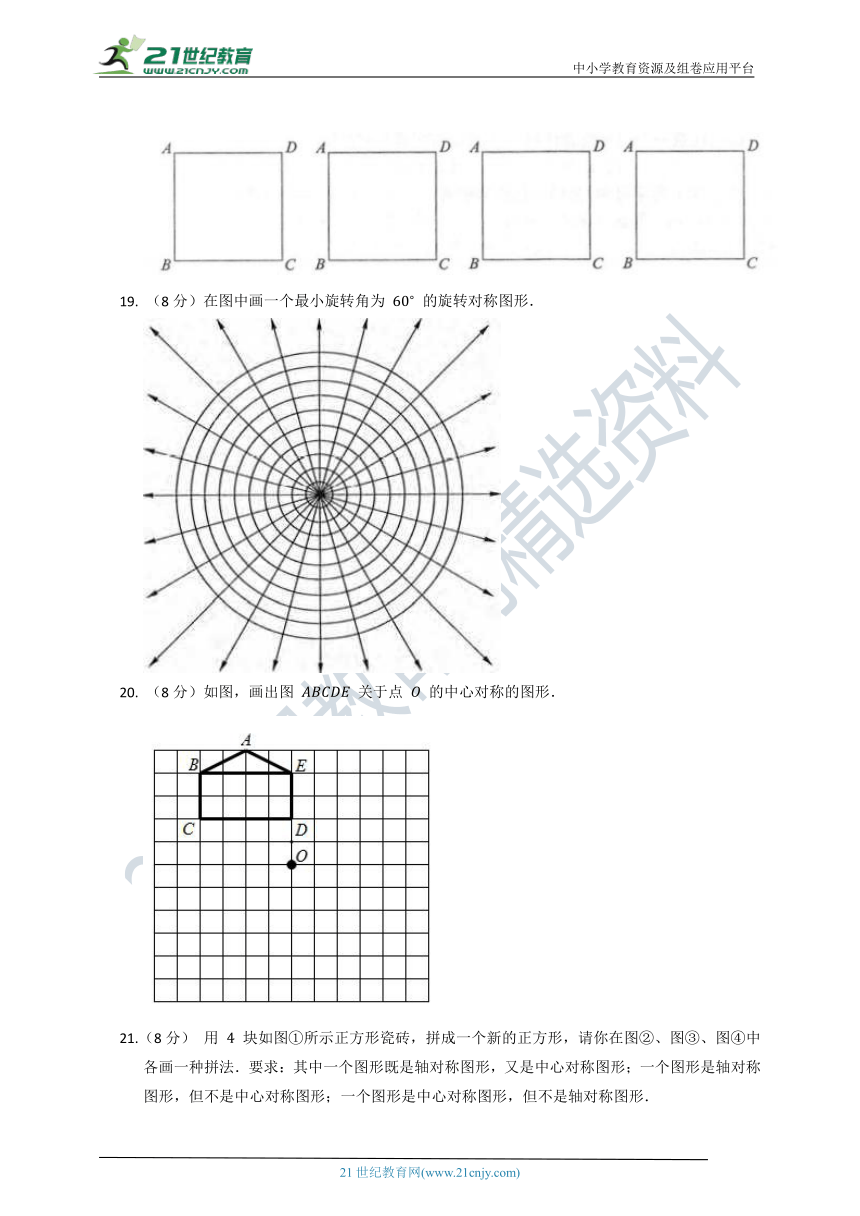
19. (8分)在图中画一个最小旋转角为 的旋转对称图形.
20. (8分)如图,画出图 关于点 的中心对称的图形.
21.(8分) 用 块如图①所示正方形瓷砖,拼成一个新的正方形,请你在图②、图③、图④中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
22.(8分) 把三角形 分别绕着边 、边 的中点 , 旋转 ,画出旋转后所得的图形.
23. (8分)如图,在等腰 中,,,且 .
(1)把 绕点 逆时针旋转 ,请画出旋转后的 的位置;
(2) 与 全等吗
(3)判断 是什么类型的三角形.
24. (8分)如图,在 中,,,点 为线段 上一动点(不与点 , 重合),作射线 ,,将射线 , 分别绕点 顺时针旋转 ,得到射线 ,,过点 作 的垂线,分别交射线 , 于点 ,.
(1)依题意补全图形.
(2)求证:.
(3)用等式表示线段 , 与 之间的数量关系,并证明.
25.(8分) 如图,已知在锐角三角形 中,,,.
(1)求点 到直线 的距离;
(2)将 绕点 旋转,点 落在点 处,点 落在点 处.
①当点 在边 上时,连接 ,求 的正弦值;
②当 时,求点 与点 的距离,
答案
第一部分
1. D
【解析】A、既是轴对称图形,也是中心对称图形,故不符题意;
B、是轴对称图形,不是中心对称图形,故不符题意;
C、既是轴对称图形,也是中心对称图形,故不符题意;
D、是中心对称图形,不是轴对称图形,故符合题意;
故选:D.
2. B
3. C
【解析】选项A、B、D中滑雪人都可以通过题图旋转得到,而选项C中滑雪人是题图通过翻折到的.
4. A
【解析】,, 是等腰直角三角形,且 ,
.
把 绕点 顺时针旋转 ,得到 ,
.
同理可得出:,,,,
,( 为自然数).
,,
.
故选:A.
5. D
6. C
7. B
【解析】设旋转角度为 ,
①当 时,,于是此小题结论错误;
②
于是此小题的结论正确;
③当旋转 时,,当旋转 时,,当旋转 时,,则在旋转过程中,两块三角板的边所在直线夹角成 的次数为 次,于是此小题结论错误;
④当 在 外时,如下图所示,
虽然 ,但 不平分 ,于是此小题的结论错误.
故选:B.
8. C
【解析】将 绕点 顺时针旋转 得到 .连接 .
是等边三角形,
,
,
,
,
,
,,
,
,
,,
,
,, 为边长的三角形 是钝角三角形,
故选:C.
9. B
【解析】A,C,D所得到的新图形不是中心对称图形,故A,C,D选项错误;B得到的新图形是中心对称图形,故B选项正确.故选B.
10. C
第二部分
11. 对称中心
12. 关于这个定点对称,成中心对称,对称中心,对称点
13. 中心对称图形,对称中心
14.
15. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
16.
【解析】如图,以 为原点建立平面直角坐标系,过点 作 延长交 于点 , 交于点 , 轴交于点 ,过点 作 轴交于点 ,
,,
设 ,,,
由旋转可得:,,,
,,
,,,
是 平分线,
,
,即可得 ,
,
设直线 的解析式为 ,
把 , 代入得:
解得:
,
当 时,,解得:,
,
,
,,
,
,
,
,
.
第三部分
17. (1) 不是;是
(2) 设小长方形的长为 ,宽为 ,
18. 如图.
19. 略
20. 略
21. 如图:
22. 略
23. (1) 图略.
(2) 全等.
因为 ,
所以 ,,
因为 ,,
所以 ,
所以 ,
即 ,
可证 .
(3) 直角三角形.
24. (1)
(2) 中,,,
,
,
,
,
射线 绕点 顺时针旋转 得到射线 ,
,
,
.
(3) .
射线 , 分别绕点 顺时针旋转 ,得到射线 ,,
,
,
又 ,,
在 和 中,
,
,,
在 中,,在 中,,
,
.
25. (1) 解 ,可知,,,,
,,,.
(2) ①如备用图 可知: 是等边 .
斜边 .
解 ,作 ,
,
,
,,
.
②Ⅰ.当 在 的右侧时,此时旋转角 ,
延长 交 于点 ,
,
,,,,
.
解 ,作 ,
,,,
.
Ⅱ.当 在 的左侧时,
此时旋转角 ,
是等边 .
.
,, 三点共线.
.
【解析】①方法二:
连接 ,
是顶角为 的等腰 ,
,
,
.
,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2022-20203学年九年级(上)第二十三章旋转检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 下列四边形中,是中心对称但不是轴对称的图形是
A. 矩形 B. 等腰梯形 C. 正方形 D. 平行四边形
2. 下列图形中,是中心对称图形,但不是轴对称图形的是
A. 等腰三角形 B. 平行四边形 C. 长方形 D. 五边形
3. 年冬季奥运会将在北京和张家口举行,如图所示的滑雪人经过旋转不能得到的是
A. B.
C. D.
4. 如图所示,在平面直角坐标系中,,, 是等腰直角三角形且 ,把 绕点 顺时针旋转 ,得到 ,把 绕点 顺时针旋转 ,得到 ,依此类推,得到的等腰直角三角形的直角顶点 的坐标为
A. B. C. D.
5. 下列图形中是中心对称图形,但不是轴对称图形的是
A. 正方形 B. 菱形 C. 矩形 D. 平行四边形
6. 将 绕点 旋转 得到 ,则下列作图正确的是
A. B.
C. D.
7. 一副三角板 、 ,如图 放置( 、 ),将三角板 绕点 逆时针旋转一定角度,如图 所示,且 ,则下列结论中正确的是
① 的角度恒为 ;
②在旋转过程中,若 平分 , 平分 , 的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成 的次数为 次;
④在图 的情况下,作 ,则 平分 .
A. ① B. ② C. ①②④ D. ①②③④
8. 如图,在等边三角形 中,在 边上取两点 ,,使 .若 ,,,则以 ,, 为边长的三角形的形状为
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随 ,, 的值而定
9. 已知图中所有的小正方形都全等,若在右侧添加一个全等的小正方形,使得到的新图形是中心对称图形,则正确的添加方案是
A. B.
C. D.
10. 线段 以点 为旋转中心,逆时针旋转 ,得到 ,再将 以点 为旋转中心逆时针旋转 得到 ,依此操作直到点 与点 重合为止,顺次连接点 , 形成的多边形是
A. 正四边形 B. 正五边形 C. 正六边形 D. 正七边形
二、填空题(共6小题;每小题3分,共18分)
11. 若两个图形成中心对称,分别联结这两个图形的两对对应点,所得两条直线的交点就是 .
12. 平面内,一个图形绕着一个定点旋转 后,能与另一个图形重合,叫做这两个图形 ,也叫做这两个图形 ,这个定点叫做 ,这两个图形中的对应点,也叫做关于这个定点的 .
13. 如果一个图形绕着所在平面内的一个定点旋转 后,能与原图形重合,那么这个图形叫做 ,这个定点叫做 .
14. 已知点 关于原点对称的点为 ,点 关于 轴对称的点为 ,点 在第四象限,那么 的取值范围是 .
15. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
16. 如图,已知在 中,,,将 绕点 逆时针旋转 后得 ,点 落在点 处,点 落在点 处,连接 ,,作 的平分线 ,交线段 于点 ,交线段 于点 ,那么 的值为 .
三、解答题(共9小题;共72分)
17. (8分)如图,下面两个图案都是由 个大小一样的小长方形拼成的,并且图()中央小正方形的边长是 厘米.问:
(1)图案()、图案()是中心对称图形吗
图() ;图() .(填:“是”或“不是”)
(2)求小长方形的长和宽.
18. (8分)为了美化环境,需要在一块正方形空地上分别种植四种不同的花草,现将这块空地按下列要求分成 块:(画出 种方法)
()分割后整个图形必须是中心对称图形;
() 块图形形状相同;
() 块图形面积相等.
19. (8分)在图中画一个最小旋转角为 的旋转对称图形.
20. (8分)如图,画出图 关于点 的中心对称的图形.
21.(8分) 用 块如图①所示正方形瓷砖,拼成一个新的正方形,请你在图②、图③、图④中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
22.(8分) 把三角形 分别绕着边 、边 的中点 , 旋转 ,画出旋转后所得的图形.
23. (8分)如图,在等腰 中,,,且 .
(1)把 绕点 逆时针旋转 ,请画出旋转后的 的位置;
(2) 与 全等吗
(3)判断 是什么类型的三角形.
24. (8分)如图,在 中,,,点 为线段 上一动点(不与点 , 重合),作射线 ,,将射线 , 分别绕点 顺时针旋转 ,得到射线 ,,过点 作 的垂线,分别交射线 , 于点 ,.
(1)依题意补全图形.
(2)求证:.
(3)用等式表示线段 , 与 之间的数量关系,并证明.
25.(8分) 如图,已知在锐角三角形 中,,,.
(1)求点 到直线 的距离;
(2)将 绕点 旋转,点 落在点 处,点 落在点 处.
①当点 在边 上时,连接 ,求 的正弦值;
②当 时,求点 与点 的距离,
答案
第一部分
1. D
【解析】A、既是轴对称图形,也是中心对称图形,故不符题意;
B、是轴对称图形,不是中心对称图形,故不符题意;
C、既是轴对称图形,也是中心对称图形,故不符题意;
D、是中心对称图形,不是轴对称图形,故符合题意;
故选:D.
2. B
3. C
【解析】选项A、B、D中滑雪人都可以通过题图旋转得到,而选项C中滑雪人是题图通过翻折到的.
4. A
【解析】,, 是等腰直角三角形,且 ,
.
把 绕点 顺时针旋转 ,得到 ,
.
同理可得出:,,,,
,( 为自然数).
,,
.
故选:A.
5. D
6. C
7. B
【解析】设旋转角度为 ,
①当 时,,于是此小题结论错误;
②
于是此小题的结论正确;
③当旋转 时,,当旋转 时,,当旋转 时,,则在旋转过程中,两块三角板的边所在直线夹角成 的次数为 次,于是此小题结论错误;
④当 在 外时,如下图所示,
虽然 ,但 不平分 ,于是此小题的结论错误.
故选:B.
8. C
【解析】将 绕点 顺时针旋转 得到 .连接 .
是等边三角形,
,
,
,
,
,
,,
,
,
,,
,
,, 为边长的三角形 是钝角三角形,
故选:C.
9. B
【解析】A,C,D所得到的新图形不是中心对称图形,故A,C,D选项错误;B得到的新图形是中心对称图形,故B选项正确.故选B.
10. C
第二部分
11. 对称中心
12. 关于这个定点对称,成中心对称,对称中心,对称点
13. 中心对称图形,对称中心
14.
15. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
16.
【解析】如图,以 为原点建立平面直角坐标系,过点 作 延长交 于点 , 交于点 , 轴交于点 ,过点 作 轴交于点 ,
,,
设 ,,,
由旋转可得:,,,
,,
,,,
是 平分线,
,
,即可得 ,
,
设直线 的解析式为 ,
把 , 代入得:
解得:
,
当 时,,解得:,
,
,
,,
,
,
,
,
.
第三部分
17. (1) 不是;是
(2) 设小长方形的长为 ,宽为 ,
18. 如图.
19. 略
20. 略
21. 如图:
22. 略
23. (1) 图略.
(2) 全等.
因为 ,
所以 ,,
因为 ,,
所以 ,
所以 ,
即 ,
可证 .
(3) 直角三角形.
24. (1)
(2) 中,,,
,
,
,
,
射线 绕点 顺时针旋转 得到射线 ,
,
,
.
(3) .
射线 , 分别绕点 顺时针旋转 ,得到射线 ,,
,
,
又 ,,
在 和 中,
,
,,
在 中,,在 中,,
,
.
25. (1) 解 ,可知,,,,
,,,.
(2) ①如备用图 可知: 是等边 .
斜边 .
解 ,作 ,
,
,
,,
.
②Ⅰ.当 在 的右侧时,此时旋转角 ,
延长 交 于点 ,
,
,,,,
.
解 ,作 ,
,,,
.
Ⅱ.当 在 的左侧时,
此时旋转角 ,
是等边 .
.
,, 三点共线.
.
【解析】①方法二:
连接 ,
是顶角为 的等腰 ,
,
,
.
,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
