人教版数学九年级上册24.1.2垂直于弦的直径同步练习(含解析)
文档属性
| 名称 | 人教版数学九年级上册24.1.2垂直于弦的直径同步练习(含解析) | 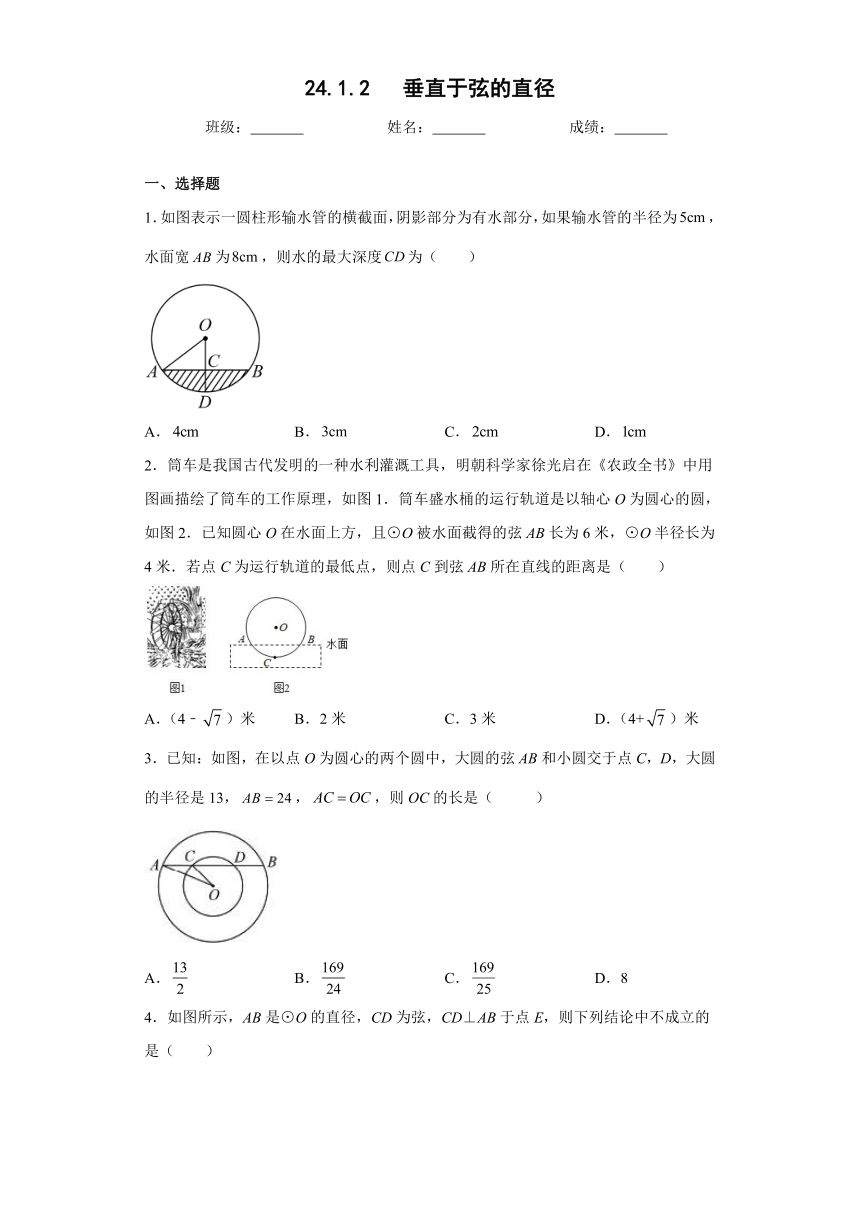 | |
| 格式 | docx | ||
| 文件大小 | 840.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 22:00:16 | ||
图片预览





文档简介
24.1.2 垂直于弦的直径
班级: 姓名: 成绩:
一、选择题
1.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为,水面宽为,则水的最大深度为( )
A. B. C. D.
2.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.(4﹣)米 B.2米 C.3米 D.(4+)米
3.已知:如图,在以点O为圆心的两个圆中,大圆的弦AB和小圆交于点C,D,大圆的半径是13,,,则OC的长是( )
A. B. C. D.8
4.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.
5.一个圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD的长为( )
A.2m B.4m C.6m D.8m
6.如图,的半径为,,经过点的的最短弦的长为( )
A.4 B.6 C.8 D.10
7.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
8.如图,矩形ABCD是由边长为1的五个小正方形拼成,O是第2个小正方形的中心,将矩形ABCD绕O点逆时针旋转90°得矩形,现用一个最小的圆覆盖这个图形,则这个圆的半径是( )
A. B. C. D.
9.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm
A.1 B.3 C.3或4 D.1或7
10.如图,点,,,在圆上,弦和交于点,则下列说法正确的是( )
A.若平分,则 B.若,则平分
C.若垂直平分,则圆心在上 D.若圆心在上,则垂直平分
11.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1或7 B.7 C.1 D.3或4
12.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是
A.5 B.6 C.7 D.8
13.如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,AB=12cm,AO=8cm,则OC长为( )cm
A.5 B.4 C. D.
14.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是( )
A.2 B. C. D.
15.如图,在⊙O中,弦AB,AC互相垂直,D,E分别为AB,AC的中点,则四边形OEAD是( )
A.梯形 B.矩形 C.菱形 D.正方形
16.如图,AB是半圆O的直径,以弦AC为折痕折叠后,恰好经过点O,则等于( )
A.120° B.125° C.130° D.145°
17.下列命题中假命题是( )
A.平分弦的半径垂直于弦 B.垂直平分弦的直线必经过圆心
C.垂直于弦的直径平分这条弦所对的弧 D.平分弧的直径垂直平分这条弧所对的弦
18.在Rt△ ABC中,∠ C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B. C. D.
19.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
20.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
二、填空题
21.如图, 在⊙O中,AB是⊙O的直径,,AB=8,M是AB上的一动点,CM+DM的最小值是_____________.
22.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=6,则⊙O半径为_______.
23.如图,矩形ABCD与圆心在AB上的☉O交于点G,B,F,E, GB =5,EF =4,那么AD =______.
24.如图,在⊙O中,弦的长为4,圆心到弦的距离为2,则的度数为______.
25.如图,A、B、C是上的点,,垂足为点D,且D为OC的中点,若,则BC的长为___________.
26.在进行垂径定理的证明教学中,老师设计了如下活动:先让同学们在圆中作了一条直径MN,然后任意作了一条弦(非直径).如图1,接下来老师提出问题:在保证弦AB长度不变的情况下,如何能找到它的中点?在同学们思考作图验证后,小华说了自己的一种想法:只要将弦AB与直径MN保持垂直关系,如图2,它们的交点就是弦AB的中点,请你说出小华此想法的依据是__.
27.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为______cm(玻璃瓶厚度忽略不计).
三、解答题
28.已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D.
(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
29.如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF
30.如图,在以点为圆心的两个同心圆中,大圆的弦交小圆于、两点.
(1)求证:;
(2)连接、,若,,,求的长.
31.学习完《垂径定理》这一节内容后,同学们学到了如何用直尺和圆规来平分一条已知弧的方法,老师接下来请小亮同学做如下四等分圆弧问题的操作:
小亮的作法如下:
如图, (1)连接AB; (2)作AB的垂直平分线CD交弧AB于点M,交AB于点T; (3)分别作线段AT,线段BT的垂直平分线EF,CH,交弧AB于N,P两点; 那么N,M,P三点把弧AB四等分.
(1)小明否定了小亮四等分弧AB作法的正确性,请你帮小明简要说明判断小亮作法错误的理由;
(2)请你利用直尺和圆规四等分所给的弧AB(仿照小亮,写出简要的作法步骤,保留作图痕迹).
32.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就,它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(寸),锯道长1尺(1尺=10寸).问这块圆形木材的直径()是多少?”如图所示,请根据所学的知识解答上述问题.
参考答案
1.C
2.A
3.B
4.C
5.B
6.C
7.A
8.C
9.D
10.C
11.A
12.B
13.D
14.A
15.B
16.A
17.A
18.A
19.B
20.A
21.8
22.
23.
24.
25.7
26.等腰三角形三线合一的性质
27.如下图所示,设球的半径为rcm,
则OG=EG-r=EF-GF-r=EF-AB-r=32-20-r=(12-r)cm,
∵EG过圆心,且垂直于AD,
∴G为AD的中点,
则AG=0.5AD=0.5×12=6cm,
在中,由勾股定理可得,
,
即,
解方程得r=7.5,
则球的半径为7.5cm.
28.(1)证明:作OE⊥AB,则AE=BE,CE=DE,
故BE﹣DE=AE﹣CE;
即AC=BD;
(2)解:连接OC,OA,
∵OE⊥AB且OE⊥CD,
∴OE=4,CE=DE,
∴DE=CE===2,
AE===4,
∴AC=AE﹣CE=4﹣2.
29.解:∵E为AB中点,MN过圆心O,
∴MN⊥AB ,
∴∠MEB=90°,
∵AB∥CD ,
∴∠MFD=∠MEB=90°,
即MN⊥CD ,
∴CF=DF.
30.(1)证明:如图,过点作于点.
,
,.
,
即.
(2)解:,,
,
,
,
,
31.(1)EF、CH平分的不是弧AM 、弧BM所对的弦;(答案不唯一),
(2)如图,点E,F,G是四等分点.
作法步骤:作AB的垂直平分线交于点F,连接AF、BF,
分别作线段AF,线段BF的垂直平分线交于点E,G,
32.设的半径为x寸,
∵,寸,
∴寸,
在中,,,
由勾股定理得,
解得.
∴的直径(寸).
答:这块圆形木材的直径()是26寸.
班级: 姓名: 成绩:
一、选择题
1.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为,水面宽为,则水的最大深度为( )
A. B. C. D.
2.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.(4﹣)米 B.2米 C.3米 D.(4+)米
3.已知:如图,在以点O为圆心的两个圆中,大圆的弦AB和小圆交于点C,D,大圆的半径是13,,,则OC的长是( )
A. B. C. D.8
4.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.
5.一个圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD的长为( )
A.2m B.4m C.6m D.8m
6.如图,的半径为,,经过点的的最短弦的长为( )
A.4 B.6 C.8 D.10
7.如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
8.如图,矩形ABCD是由边长为1的五个小正方形拼成,O是第2个小正方形的中心,将矩形ABCD绕O点逆时针旋转90°得矩形,现用一个最小的圆覆盖这个图形,则这个圆的半径是( )
A. B. C. D.
9.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm
A.1 B.3 C.3或4 D.1或7
10.如图,点,,,在圆上,弦和交于点,则下列说法正确的是( )
A.若平分,则 B.若,则平分
C.若垂直平分,则圆心在上 D.若圆心在上,则垂直平分
11.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1或7 B.7 C.1 D.3或4
12.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是
A.5 B.6 C.7 D.8
13.如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,AB=12cm,AO=8cm,则OC长为( )cm
A.5 B.4 C. D.
14.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是( )
A.2 B. C. D.
15.如图,在⊙O中,弦AB,AC互相垂直,D,E分别为AB,AC的中点,则四边形OEAD是( )
A.梯形 B.矩形 C.菱形 D.正方形
16.如图,AB是半圆O的直径,以弦AC为折痕折叠后,恰好经过点O,则等于( )
A.120° B.125° C.130° D.145°
17.下列命题中假命题是( )
A.平分弦的半径垂直于弦 B.垂直平分弦的直线必经过圆心
C.垂直于弦的直径平分这条弦所对的弧 D.平分弧的直径垂直平分这条弧所对的弦
18.在Rt△ ABC中,∠ C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B. C. D.
19.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
20.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
二、填空题
21.如图, 在⊙O中,AB是⊙O的直径,,AB=8,M是AB上的一动点,CM+DM的最小值是_____________.
22.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=6,则⊙O半径为_______.
23.如图,矩形ABCD与圆心在AB上的☉O交于点G,B,F,E, GB =5,EF =4,那么AD =______.
24.如图,在⊙O中,弦的长为4,圆心到弦的距离为2,则的度数为______.
25.如图,A、B、C是上的点,,垂足为点D,且D为OC的中点,若,则BC的长为___________.
26.在进行垂径定理的证明教学中,老师设计了如下活动:先让同学们在圆中作了一条直径MN,然后任意作了一条弦(非直径).如图1,接下来老师提出问题:在保证弦AB长度不变的情况下,如何能找到它的中点?在同学们思考作图验证后,小华说了自己的一种想法:只要将弦AB与直径MN保持垂直关系,如图2,它们的交点就是弦AB的中点,请你说出小华此想法的依据是__.
27.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为______cm(玻璃瓶厚度忽略不计).
三、解答题
28.已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D.
(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
29.如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF
30.如图,在以点为圆心的两个同心圆中,大圆的弦交小圆于、两点.
(1)求证:;
(2)连接、,若,,,求的长.
31.学习完《垂径定理》这一节内容后,同学们学到了如何用直尺和圆规来平分一条已知弧的方法,老师接下来请小亮同学做如下四等分圆弧问题的操作:
小亮的作法如下:
如图, (1)连接AB; (2)作AB的垂直平分线CD交弧AB于点M,交AB于点T; (3)分别作线段AT,线段BT的垂直平分线EF,CH,交弧AB于N,P两点; 那么N,M,P三点把弧AB四等分.
(1)小明否定了小亮四等分弧AB作法的正确性,请你帮小明简要说明判断小亮作法错误的理由;
(2)请你利用直尺和圆规四等分所给的弧AB(仿照小亮,写出简要的作法步骤,保留作图痕迹).
32.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就,它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(寸),锯道长1尺(1尺=10寸).问这块圆形木材的直径()是多少?”如图所示,请根据所学的知识解答上述问题.
参考答案
1.C
2.A
3.B
4.C
5.B
6.C
7.A
8.C
9.D
10.C
11.A
12.B
13.D
14.A
15.B
16.A
17.A
18.A
19.B
20.A
21.8
22.
23.
24.
25.7
26.等腰三角形三线合一的性质
27.如下图所示,设球的半径为rcm,
则OG=EG-r=EF-GF-r=EF-AB-r=32-20-r=(12-r)cm,
∵EG过圆心,且垂直于AD,
∴G为AD的中点,
则AG=0.5AD=0.5×12=6cm,
在中,由勾股定理可得,
,
即,
解方程得r=7.5,
则球的半径为7.5cm.
28.(1)证明:作OE⊥AB,则AE=BE,CE=DE,
故BE﹣DE=AE﹣CE;
即AC=BD;
(2)解:连接OC,OA,
∵OE⊥AB且OE⊥CD,
∴OE=4,CE=DE,
∴DE=CE===2,
AE===4,
∴AC=AE﹣CE=4﹣2.
29.解:∵E为AB中点,MN过圆心O,
∴MN⊥AB ,
∴∠MEB=90°,
∵AB∥CD ,
∴∠MFD=∠MEB=90°,
即MN⊥CD ,
∴CF=DF.
30.(1)证明:如图,过点作于点.
,
,.
,
即.
(2)解:,,
,
,
,
,
31.(1)EF、CH平分的不是弧AM 、弧BM所对的弦;(答案不唯一),
(2)如图,点E,F,G是四等分点.
作法步骤:作AB的垂直平分线交于点F,连接AF、BF,
分别作线段AF,线段BF的垂直平分线交于点E,G,
32.设的半径为x寸,
∵,寸,
∴寸,
在中,,,
由勾股定理得,
解得.
∴的直径(寸).
答:这块圆形木材的直径()是26寸.
同课章节目录
