人教版数学九年级上册24.4扇形的弧长与面积专项培优练习(含解析)
文档属性
| 名称 | 人教版数学九年级上册24.4扇形的弧长与面积专项培优练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 742.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览


文档简介
人教版数学九年级上册专项培优练习
《圆-扇形的弧长与面积》
一 、选择题
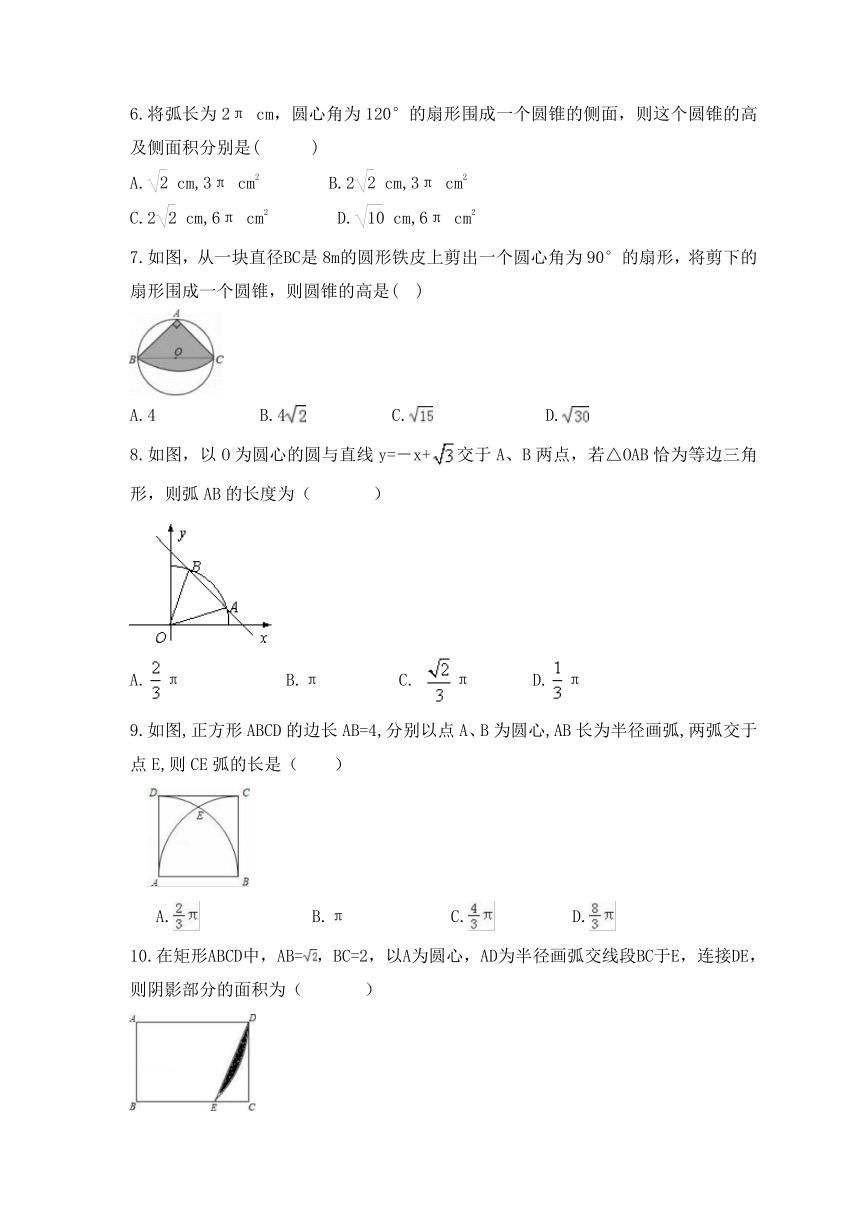
1.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π B.4π C.5π D.6π
2.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A.10π B. C.π D.π
3.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到点A′的位置,则图中阴影部分的面积为( )
A.π B.2π C. D.4π
4.如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
A.2cm2 B.4cm2 C.4cm2 D.πcm2
5.用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是( )
A.10 B.20 C.10π D.20π
6.将弧长为2π cm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
A. cm,3π cm2 B.2 cm,3π cm2
C.2 cm,6π cm2 D. cm,6π cm2
7.如图,从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,则圆锥的高是( )
A.4 B.4 C. D.
8.如图,以O为圆心的圆与直线y=-x+交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
A.π B.π C. π D.π
9.如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
A. B.π C. D.
10.在矩形ABCD中,AB=,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,
则阴影部分的面积为( )
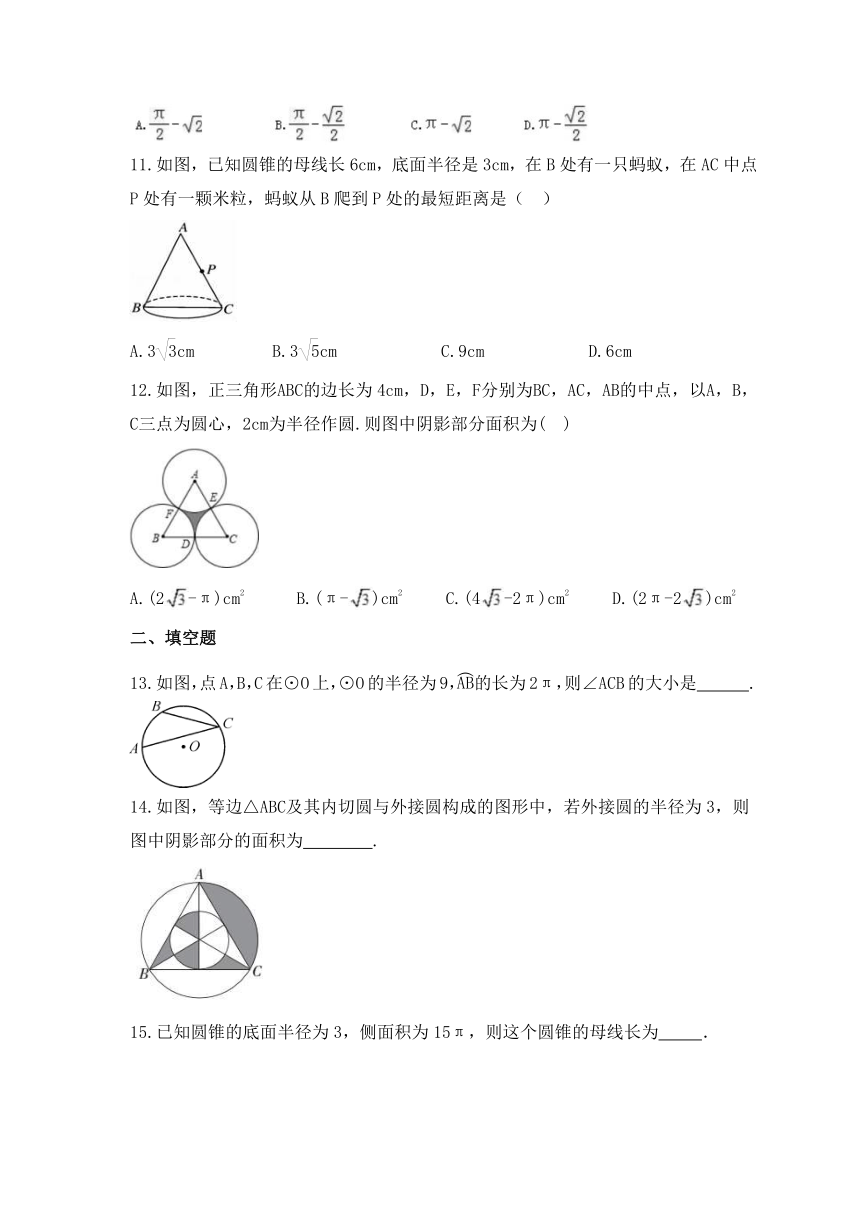
11.如图,已知圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )
A.3cm B.3cm C.9cm D.6cm
12.如图,正三角形ABC的边长为4cm,D,E,F分别为BC,AC,AB的中点,以A,B,C三点为圆心,2cm为半径作圆.则图中阴影部分面积为( )
A.(2-π)cm2 B.(π-)cm2 C.(4-2π)cm2 D.(2π-2)cm2
二 、填空题
13.如图,点A,B,C在⊙O上,⊙O的半径为9,的长为2π,则∠ACB的大小是 .
14.如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则图中阴影部分的面积为 .
15.已知圆锥的底面半径为3,侧面积为15π,则这个圆锥的母线长为 .
16.如图,方格纸中4个小正方形边长均为1,则图中阴影部分三个小扇形面积和为________.(结果保留π)
17.如图,在Rt△ABC中,AC=4,BC=3,绕其中一条线段旋转一周,所得图形的最小表面积为____.
18.如图,⊙O的直径为16,AB、CD是互相垂直的两条直径,点P是弧AD上任意一点,经过P作PM⊥AB于M,PN⊥CD于N,点Q是MN的中点,当点P沿着弧AD从点A移动到终点D时,点Q走过的路径长为 .
三 、解答题
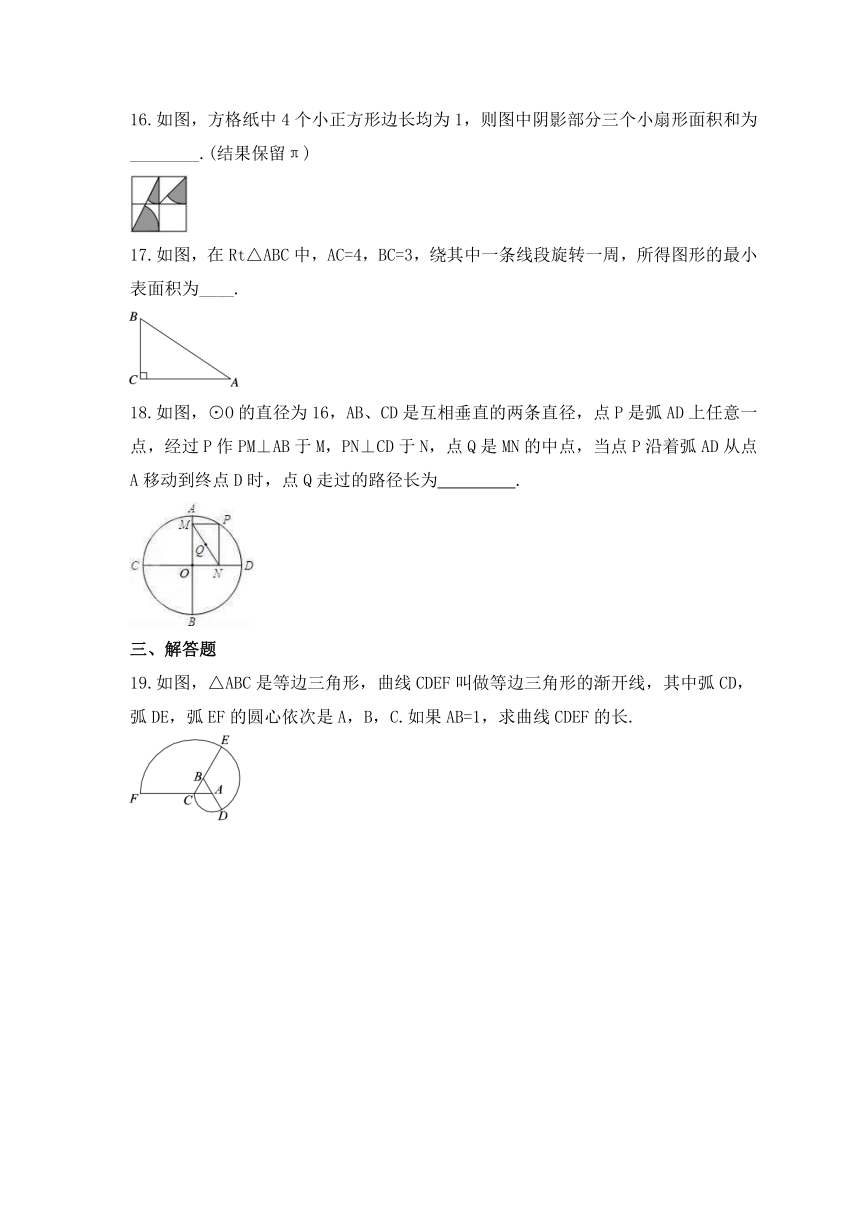
19.如图,△ABC是等边三角形,曲线CDEF叫做等边三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C.如果AB=1,求曲线CDEF的长.
20.如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
21.如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
22.如图,有一直径是 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形BAC.
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为多少米.
23.如图,有一个直径为米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形纸片围成一个圆锥,则圆锥的底面圆半径是多少?
(3)求圆锥的全面积.
24.如图,在扇形AOB中,OA、OB是半径,且OA=4,∠AOB=120°.点P是弧AB上的一个动点,连接AP、BP,分别作OC⊥PA,OD⊥PB,垂足分别为C、D,连接CD.
(1)如图①,在点P的移动过程中,线段CD的长是否会发生变化?若不发生变化,请求出线段CD的长;若会发生变化,请说明理由;
(2)如图②,若点M、N为弧AB的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
参考答案
1.B
2.C;
3.B
4.B
5.A
6.B.
7.D
8.C
9.A
10.A
11.B
12.C
13.答案为:20°.
14.答案为:3π.
15.答案为5.
16.答案为:
17.答案为:π.
18.答案为:2π.
19.解:的长是=,
的长是=,
的长是=2π,
则曲线CDEF的长是++2π=4π.
20.解:(1)证明:∵点C、D为半圆O的三等分点,
∴,
∴∠BOC=∠A,
∴OC∥AD,
∵CE⊥AD,
∴CE⊥OC,
∴CE为⊙O的切线;
(2)解:连接OD,OC,
∵,
∴∠COD=×180°=60°,
∵CD∥AB,
∴S△ACD=S△COD,
∴图中阴影部分的面积=S扇形COD=.
21.证明:(1)连接OD,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
又∵OD=OB,
∴∠ODB=∠OBD,
∵DE⊥BC,
∴∠E=90°,
∴∠CBD+∠BDE=90°,
∴∠ODB+∠BDE=90°,
即OD⊥DE,
∴DE是⊙O的切线;
(2)∵DF⊥AB,
∴∠DFB=90°=∠E,
又∵∠ABD=∠CBD=∠ABC=30°,BD=BD,
∴△BDF≌△BDE(AAS)
∴BF=BE=3,
在Rt△BDF中,∠FBD=30°,BF=3,
∴DF=tan30°×BF=3,
在Rt△ODF中,∠DOF=2∠OBD=30°×2=60°,DF=3,
∴OF=tan30°×DF=,OD=2 OF=2,
∴S阴影=S扇形OAD﹣S△ODF=2π﹣.
22.解:(1)如图,连结BC.
∵∠BAC=90°,
∴BC为⊙O的直径,即BC= m,
∴AB=BC=1(m);
(2)设所得圆锥的底面圆的半径为r(m),
由题意,得2πr=,解得r=.
答:圆锥的底面圆的半径为 m.
23.解:(1)连接BC.
∵∠A=90°,
∴BC为⊙O的直径,
∴AB=AC=1米.
则被剪掉的阴影部分的面积为π×()2-=(米2).
(2)圆锥的底面圆半径为÷2π=(米).
(3)圆锥的全面积为+π×()2=π(米2).
24.解:(1)线段CD的长不会发生变化.
连接AB,过O作OH⊥AB于H.
∵OC⊥PA,OD⊥PB,
∴AC=PC,BD=PD.
∴CD=0.5AB.
∵OA=OB,OH⊥AB,
∴AH=BH=0.5AB,∠AOH=0.5∠AOB=60°.
在Rt△AOH中,∵∠OAH=30°,∴OH=2.
∴在Rt△AOH,由勾股定理得AH=.
∴AB=.∴CD=.
(2).
《圆-扇形的弧长与面积》
一 、选择题
1.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π B.4π C.5π D.6π
2.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A.10π B. C.π D.π
3.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到点A′的位置,则图中阴影部分的面积为( )
A.π B.2π C. D.4π
4.如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
A.2cm2 B.4cm2 C.4cm2 D.πcm2
5.用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是( )
A.10 B.20 C.10π D.20π
6.将弧长为2π cm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
A. cm,3π cm2 B.2 cm,3π cm2
C.2 cm,6π cm2 D. cm,6π cm2
7.如图,从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,则圆锥的高是( )
A.4 B.4 C. D.
8.如图,以O为圆心的圆与直线y=-x+交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
A.π B.π C. π D.π
9.如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
A. B.π C. D.
10.在矩形ABCD中,AB=,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,
则阴影部分的面积为( )
11.如图,已知圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )
A.3cm B.3cm C.9cm D.6cm
12.如图,正三角形ABC的边长为4cm,D,E,F分别为BC,AC,AB的中点,以A,B,C三点为圆心,2cm为半径作圆.则图中阴影部分面积为( )
A.(2-π)cm2 B.(π-)cm2 C.(4-2π)cm2 D.(2π-2)cm2
二 、填空题
13.如图,点A,B,C在⊙O上,⊙O的半径为9,的长为2π,则∠ACB的大小是 .
14.如图,等边△ABC及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则图中阴影部分的面积为 .
15.已知圆锥的底面半径为3,侧面积为15π,则这个圆锥的母线长为 .
16.如图,方格纸中4个小正方形边长均为1,则图中阴影部分三个小扇形面积和为________.(结果保留π)
17.如图,在Rt△ABC中,AC=4,BC=3,绕其中一条线段旋转一周,所得图形的最小表面积为____.
18.如图,⊙O的直径为16,AB、CD是互相垂直的两条直径,点P是弧AD上任意一点,经过P作PM⊥AB于M,PN⊥CD于N,点Q是MN的中点,当点P沿着弧AD从点A移动到终点D时,点Q走过的路径长为 .
三 、解答题
19.如图,△ABC是等边三角形,曲线CDEF叫做等边三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C.如果AB=1,求曲线CDEF的长.
20.如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
21.如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
22.如图,有一直径是 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形BAC.
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为多少米.
23.如图,有一个直径为米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形纸片围成一个圆锥,则圆锥的底面圆半径是多少?
(3)求圆锥的全面积.
24.如图,在扇形AOB中,OA、OB是半径,且OA=4,∠AOB=120°.点P是弧AB上的一个动点,连接AP、BP,分别作OC⊥PA,OD⊥PB,垂足分别为C、D,连接CD.
(1)如图①,在点P的移动过程中,线段CD的长是否会发生变化?若不发生变化,请求出线段CD的长;若会发生变化,请说明理由;
(2)如图②,若点M、N为弧AB的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
参考答案
1.B
2.C;
3.B
4.B
5.A
6.B.
7.D
8.C
9.A
10.A
11.B
12.C
13.答案为:20°.
14.答案为:3π.
15.答案为5.
16.答案为:
17.答案为:π.
18.答案为:2π.
19.解:的长是=,
的长是=,
的长是=2π,
则曲线CDEF的长是++2π=4π.
20.解:(1)证明:∵点C、D为半圆O的三等分点,
∴,
∴∠BOC=∠A,
∴OC∥AD,
∵CE⊥AD,
∴CE⊥OC,
∴CE为⊙O的切线;
(2)解:连接OD,OC,
∵,
∴∠COD=×180°=60°,
∵CD∥AB,
∴S△ACD=S△COD,
∴图中阴影部分的面积=S扇形COD=.
21.证明:(1)连接OD,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
又∵OD=OB,
∴∠ODB=∠OBD,
∵DE⊥BC,
∴∠E=90°,
∴∠CBD+∠BDE=90°,
∴∠ODB+∠BDE=90°,
即OD⊥DE,
∴DE是⊙O的切线;
(2)∵DF⊥AB,
∴∠DFB=90°=∠E,
又∵∠ABD=∠CBD=∠ABC=30°,BD=BD,
∴△BDF≌△BDE(AAS)
∴BF=BE=3,
在Rt△BDF中,∠FBD=30°,BF=3,
∴DF=tan30°×BF=3,
在Rt△ODF中,∠DOF=2∠OBD=30°×2=60°,DF=3,
∴OF=tan30°×DF=,OD=2 OF=2,
∴S阴影=S扇形OAD﹣S△ODF=2π﹣.
22.解:(1)如图,连结BC.
∵∠BAC=90°,
∴BC为⊙O的直径,即BC= m,
∴AB=BC=1(m);
(2)设所得圆锥的底面圆的半径为r(m),
由题意,得2πr=,解得r=.
答:圆锥的底面圆的半径为 m.
23.解:(1)连接BC.
∵∠A=90°,
∴BC为⊙O的直径,
∴AB=AC=1米.
则被剪掉的阴影部分的面积为π×()2-=(米2).
(2)圆锥的底面圆半径为÷2π=(米).
(3)圆锥的全面积为+π×()2=π(米2).
24.解:(1)线段CD的长不会发生变化.
连接AB,过O作OH⊥AB于H.
∵OC⊥PA,OD⊥PB,
∴AC=PC,BD=PD.
∴CD=0.5AB.
∵OA=OB,OH⊥AB,
∴AH=BH=0.5AB,∠AOH=0.5∠AOB=60°.
在Rt△AOH中,∵∠OAH=30°,∴OH=2.
∴在Rt△AOH,由勾股定理得AH=.
∴AB=.∴CD=.
(2).
同课章节目录
