2022-2023学年沪科版九年级上册数学(21.1-21.4.1)专项测试(含答案)
文档属性
| 名称 | 2022-2023学年沪科版九年级上册数学(21.1-21.4.1)专项测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 196.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 22:18:16 | ||
图片预览


文档简介
沪科版九年级上册数学(21.1-21.4.1)专项测试
一、单选题(共40分)
1.已知y=(m+2)+2是关于x的二次函数,那么m的值为( )
A.-2 B.2 C.±2 D.0
2.把抛物线的图象向左平移2个单位,再向上平移3个单位,所得的抛物线是( )
A. B. C. D.
3.已知抛物线y=ax2+bx+c(a≠0)与y=x2-4x+3关于x轴对称,则a,b,c的值分别是( )
A.-1,4,-3 B.-1,-4,-3 C.-1,4,3 D.-1,-4,3
4.下表是二次函数的对应值,那么方程x2﹣5x+c=0的一个近似根是( ):
x … 1.3 1.4 1.5 1.6 1.7 …
y … 0.36 0.13 ﹣0.08 ﹣0.27 ﹣0.44 …
A.1.4 B.1.5 C.1.6 D.1.7
5.,,都在二次函数的图象上,则,,的大小关系为( )
A. B. C. D.
6.在同一直角坐标系中,函数和函数 (a是常数,且a≠0)的图象可能是( )
A. B. C. D.
7.如表中列出的是二次函数y=a+bx+c中x与y的几组对应值,下列各选项中正确的是( )
x … ﹣2 0 1 3 …
y … 6 ﹣4 ﹣6 ﹣4 …
A.这个函数的图象开口向下 B.这个函数的图象与x轴有两个交点,且都在y轴同侧
C.当x>1时,y的值随x值的增大而增大 D.方程a+(b+2)x+c=﹣4的解为=0,=1
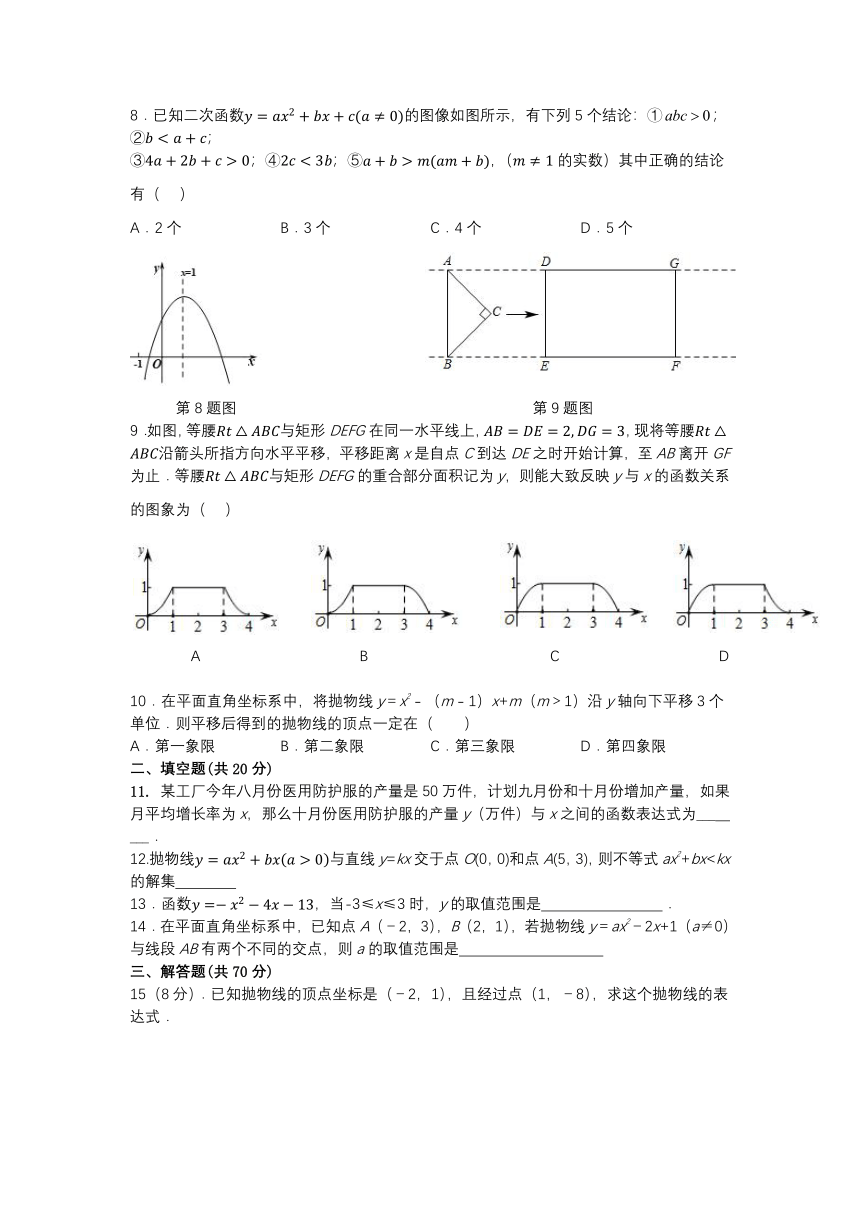
8.已知二次函数的图像如图所示,有下列5个结论:①;②;
③;④;⑤,(的实数)其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
第8题图 第9题图
9.如图,等腰与矩形DEFG在同一水平线上,,现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A B C D
10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题(共20分)
11. 某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x,那么十月份医用防护服的产量y(万件)与x之间的函数表达式为___ ___.
12.抛物线与直线y=kx交于点O(0,0)和点A(5,3),则不等式ax2+bx13.函数,当-3≤x≤3时,y的取值范围是 .
14.在平面直角坐标系中,已知点A(-2,3),B(2,1),若抛物线y=ax2-2x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是
三、解答题(共70分)
15(8分).已知抛物线的顶点坐标是(-2,1),且经过点(1,-8),求这个抛物线的表达式.
16(8分)已知二次函数y=﹣(x+4)2,将此函数的向右平移3个单位长度,再向上平移2个单位长度.
(1)请写出平移后图像所对应的函数解析式:
(2)在如图所示的平面直角坐标系中,画出平移后的图像;
(3)根据所画的函数图像,写出当y<0时x的取值范围:
17.(8分)二次函数的图象与直线y=2x-1交于点P(1,m).
(1)求a、m的值;
(2)写出二次函数的解析式,指出抛物线的顶点坐标和对称轴.
18.(8分)抛物线与轴交于点A(1,0),B(5,0),点为轴正半轴上一点,直线轴交抛物线于点,(点在点左侧).
(1)求该抛物线的表达式;
(2)若,求点的坐标.
19.(10分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
(1)写出方程ax2+bx+c=0的两个根: ;
(2)写出不等式ax2+bx+c>0的解集: ;
(3)写出y随x的增大而增大的自变量x的取值范围: ;
(4)若方程ax2+bx+c+k=0有两个不相等的实数根,直接写出k的取值范围: .
20.(10分)抛物线y=-x2+(a+1)x-a与x轴交于A,B两点,与y轴交于点C,已知△BAC的面积是6.
(1)求a的值
(2)在抛物线上是否存在异于点C的另一点P,使S△ABP=S△ABC.,
若存在,请求出点P的坐标,若不存在,请说明理由.
21.(12分)已知二次函数y=x2-2mx+2m2+1(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点.
(2)如果把该函数图象沿y轴向下平移5个单位长度后,得到的函数图象与x轴只有一个公共点,求m的值.
22.(12分)一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
23.(14分)如图①,抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图②,连接BC,点E是第四象限内抛物线上的动点,过点E作EF⊥BC于点F,EGy轴交BC于点G,求△EFG面积的最大值及此时点E的坐标;
答 案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A B B D D B A D
y=50(1+x)2 12.0y=-(x+2)2+1 16.(1) y=-0.5(x+1)2+2 (3)x>1或x<-3 17.a=1 ,m=1 (2) y=x2,顶点(0,0),对称轴x=0 18.y=-x2+6x-5 (2)(4,3) 19.(1)x=1或x=3;(2)1-2
一、单选题(共40分)
1.已知y=(m+2)+2是关于x的二次函数,那么m的值为( )
A.-2 B.2 C.±2 D.0
2.把抛物线的图象向左平移2个单位,再向上平移3个单位,所得的抛物线是( )
A. B. C. D.
3.已知抛物线y=ax2+bx+c(a≠0)与y=x2-4x+3关于x轴对称,则a,b,c的值分别是( )
A.-1,4,-3 B.-1,-4,-3 C.-1,4,3 D.-1,-4,3
4.下表是二次函数的对应值,那么方程x2﹣5x+c=0的一个近似根是( ):
x … 1.3 1.4 1.5 1.6 1.7 …
y … 0.36 0.13 ﹣0.08 ﹣0.27 ﹣0.44 …
A.1.4 B.1.5 C.1.6 D.1.7
5.,,都在二次函数的图象上,则,,的大小关系为( )
A. B. C. D.
6.在同一直角坐标系中,函数和函数 (a是常数,且a≠0)的图象可能是( )
A. B. C. D.
7.如表中列出的是二次函数y=a+bx+c中x与y的几组对应值,下列各选项中正确的是( )
x … ﹣2 0 1 3 …
y … 6 ﹣4 ﹣6 ﹣4 …
A.这个函数的图象开口向下 B.这个函数的图象与x轴有两个交点,且都在y轴同侧
C.当x>1时,y的值随x值的增大而增大 D.方程a+(b+2)x+c=﹣4的解为=0,=1
8.已知二次函数的图像如图所示,有下列5个结论:①;②;
③;④;⑤,(的实数)其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
第8题图 第9题图
9.如图,等腰与矩形DEFG在同一水平线上,,现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A B C D
10.在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题(共20分)
11. 某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x,那么十月份医用防护服的产量y(万件)与x之间的函数表达式为___ ___.
12.抛物线与直线y=kx交于点O(0,0)和点A(5,3),则不等式ax2+bx
14.在平面直角坐标系中,已知点A(-2,3),B(2,1),若抛物线y=ax2-2x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是
三、解答题(共70分)
15(8分).已知抛物线的顶点坐标是(-2,1),且经过点(1,-8),求这个抛物线的表达式.
16(8分)已知二次函数y=﹣(x+4)2,将此函数的向右平移3个单位长度,再向上平移2个单位长度.
(1)请写出平移后图像所对应的函数解析式:
(2)在如图所示的平面直角坐标系中,画出平移后的图像;
(3)根据所画的函数图像,写出当y<0时x的取值范围:
17.(8分)二次函数的图象与直线y=2x-1交于点P(1,m).
(1)求a、m的值;
(2)写出二次函数的解析式,指出抛物线的顶点坐标和对称轴.
18.(8分)抛物线与轴交于点A(1,0),B(5,0),点为轴正半轴上一点,直线轴交抛物线于点,(点在点左侧).
(1)求该抛物线的表达式;
(2)若,求点的坐标.
19.(10分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
(1)写出方程ax2+bx+c=0的两个根: ;
(2)写出不等式ax2+bx+c>0的解集: ;
(3)写出y随x的增大而增大的自变量x的取值范围: ;
(4)若方程ax2+bx+c+k=0有两个不相等的实数根,直接写出k的取值范围: .
20.(10分)抛物线y=-x2+(a+1)x-a与x轴交于A,B两点,与y轴交于点C,已知△BAC的面积是6.
(1)求a的值
(2)在抛物线上是否存在异于点C的另一点P,使S△ABP=S△ABC.,
若存在,请求出点P的坐标,若不存在,请说明理由.
21.(12分)已知二次函数y=x2-2mx+2m2+1(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点.
(2)如果把该函数图象沿y轴向下平移5个单位长度后,得到的函数图象与x轴只有一个公共点,求m的值.
22.(12分)一大型商场经营某种品牌商品,该商品的进价为每件6元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,表格记录的是某三周的有关数据:
x(元/件) 7 8 9
y(件) 8500 8000 7500
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于17元/件,若某一周该商品的销售最不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
23.(14分)如图①,抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图②,连接BC,点E是第四象限内抛物线上的动点,过点E作EF⊥BC于点F,EGy轴交BC于点G,求△EFG面积的最大值及此时点E的坐标;
答 案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A B B D D B A D
y=50(1+x)2 12.0
