人教版数学九年级上册24.1 圆的有关性质 综合强化练(含答案)
文档属性
| 名称 | 人教版数学九年级上册24.1 圆的有关性质 综合强化练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 539.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 11:20:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册综合强化练6
【练习范围:24.1 满分:100分】
一、选择题(每小题4分,共32分)
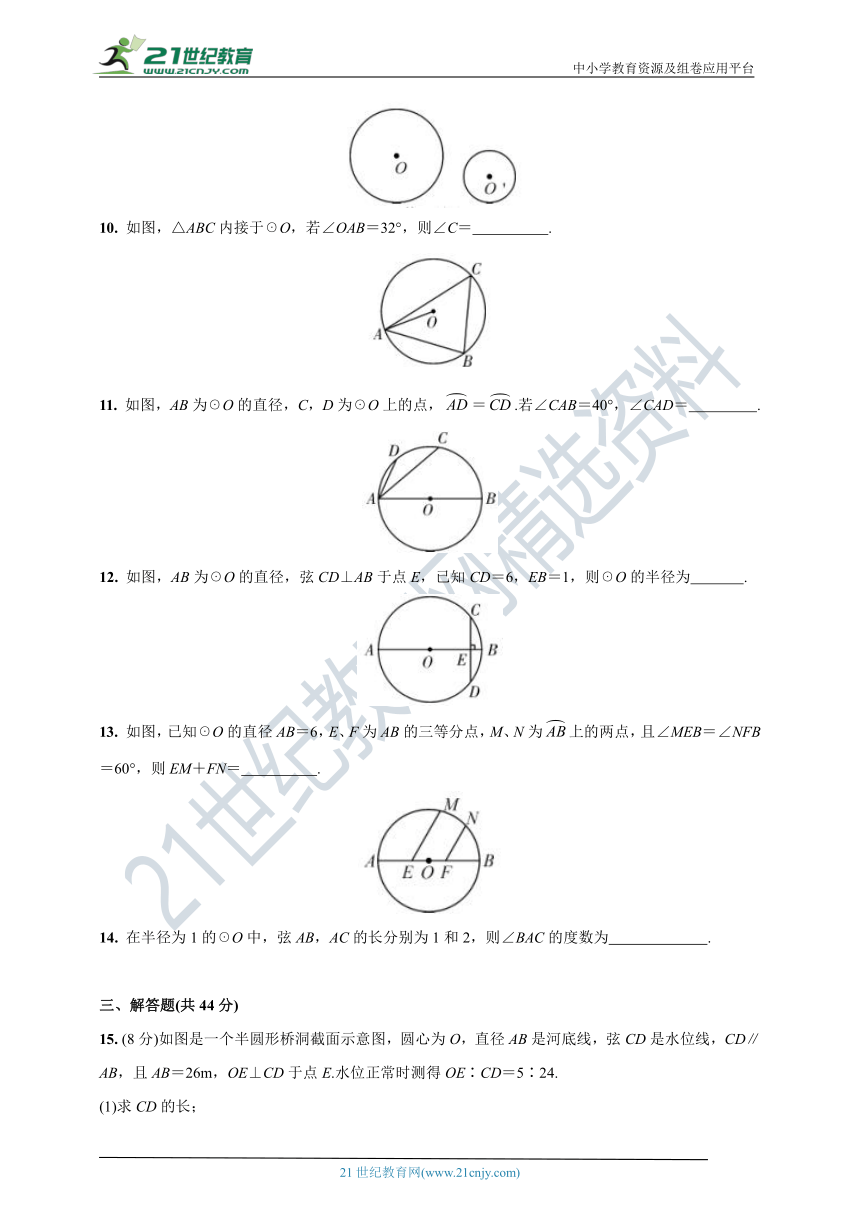
1. 如图,点A、B、C都在☉O上,且点C在弦AB所对的优弧上,如果∠AOB=64°,那∠ACB的度数是( )
A.26° B.30° C.32° D.64°
2. 如图,在☉O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB B.CE=EO C.∠OCE=40° D.∠BOC=2∠BAD
3. 如图,A,B,C,D是☉O上的四点,且AD=BC,则AB与CD的大小关系为( )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
4. 如图,CD为☉O的直径,弦AB⊥CD,垂足为M,若AB=12.OM∶MD=5∶8,则☉O的周长为( )
A.26π B.13π C. D.
5. 如图,点A、B、C在☉O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
6. 如图,C,D是以线段AB为直径的☉O上两点,若CA=CD,且∠ACD=40°,则∠CAB等于( )
A.10° B.20° C.30° D.40°
7. 如图,☉O的半径是2,AB是☉O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( )
A.60° B.120° C.60°或120° D.30°或150°
8. 如图,AB是☉O的直径,C,D是☉O上的点,且OC∥BD,AD分别与BC,OC相交于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED. 其中一定成立的是( )
A.②④⑤⑥ B.①③⑤⑥ C.②③④⑥ D.①③④⑤
二、填空题(每小题4分,共24分)
9. 如图所示,☉O与☉O′是任意的两个圆,把这两个圆看作一个整体,它是一个轴对称图形,这个图形的对称轴是 .
10. 如图,△ABC内接于☉O,若∠OAB=32°,则∠C= .
11. 如图,AB为☉O的直径,C,D为☉O上的点,=.若∠CAB=40°,∠CAD= .
12. 如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 .
13. 如图,已知☉O的直径AB=6,E、F为AB的三等分点,M、N为上的两点,且∠MEB=∠NFB=60°,则EM+FN= .
14. 在半径为1的☉O中,弦AB,AC的长分别为1和2,则∠BAC的度数为 .
三、解答题(共44分)
15. (8分)如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥
AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE∶CD=5∶24.
(1)求CD的长;
(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满
16. (8分)如图,在☉O中,AB、CD为互相垂直的两条弦,垂足为点E.当☉O的半径为2,AB2+CD2=28,求OE的长.
17. (8分)如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆☉O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若☉O的直径为2,求PC2+PB2的值.
18. (10分)如图,AB是☉O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,则☉O的半径为 ,CE的长是 .
19. (10分)如图,在平面直角坐标系中,以点M(0,)为圆心,以2为半径作☉M交x轴于A、B两点,交y轴于C、D两点,连接AM并延长交☉M于P点,连接PC交x轴于点E.
(1)求点C、P的坐标;
(2)求证:BE=2OE.
参 考 答 案
一、选择题(每小题4分,共32分)
1. C 2. D 3. B 4. B 5. B 6. B 7. C 8. D
二、填空题(每小题4分,共24分)
9. 直线OO′
10. 58°
11. 25°
12. 5
13.
14. 15°或105°
三、解答题(共44分)
15. (8分)
解:(1)∵直径AB=26m,∴OD=AB=×26=13(m). ∵OE⊥CD,∴DE=CD. ∵OE∶CD=5∶24,∴OE∶ED=5∶12,∴设OE=5x,ED=12x. ∴在Rt△ODE中,(5x)2+(12x)2=132. 解得x=1. ∴CD=2DE=2×12×1=24(m).
(2)由(1)得OE=1×5=5(m),延长OE交圆O于点F,∴EF=OF-OE=13-5=8(m). ∴8÷4=2(小时),即经过2小时桥洞会刚刚被灌满.
16. (8分)
解:如图,过点O分别作OM⊥CD,ON⊥AB,垂足分别为M,N,连接OC,OB,∵AB⊥CD,OM⊥CD,ON⊥AB,∴四边形OMEN是矩形,∴ON=ME,OM=EN. 在Rt△COM中,OC2-CM2=OM2. 在Rt△BON中,OB2-BN2=ON2,而BN=AB,CM=CD,∴OE2=MO2+ON2=OC2-CM2+OB2-BN2=2OB2-(AB2+CD2),又∵⊙O的半径为2,AB2+CD2=28,∴OE2=8-7=1,即OE=1.
17. (8分)
(1)证明:∵△ABC是等腰直角三角形,∴AC=AB,∠CAB=90°,∠PBA=45°,∴∠PEA=∠PBA=45°. ∵PE为⊙O的直径,∴∠PAE=90°,∴∠APE=∠PEA=45°,∴△APE为等腰直角三角形;
(2)解:∵∠PAE=∠CAB=90°,∴∠CAB-∠PAB=∠PAE-∠PAB,∴∠CAP=∠BAE,∴△CAP≌△BAE(SAS),∴PC=BE. ∵∠PBE=90°,∴在Rt△PBE中,BE2+PB2=PE2=4. ∴PC2+PB2=4.
18. (10分)
(1)证明:∵AB为⊙O直径,∴∠ACB=90°,∴∠A+∠CBA=90°. 又CE⊥AB,∴∠ECB+∠CBA=90°,∴∠BCE=∠A,又=,∴∠A=∠CBD,∴∠ECB=∠DBC,∴CF=BF.
(2)半径为5,CE===4.8.
19. (10分)(1)解:连接PB,∵PA是⊙M的直径,∴∠PBA=90°,又∵MO⊥AB,∴PB∥MO,∴PB=2OM=2. 在Rt△ABP中,AP=4,PB=2,根据勾股定理,得AB=6,∴AO=OB=3. ∴P点坐标为(3,2).圆的半径MC=2,又OM=,所以OC=MC-OM=,则点C的坐标为(0,-).
(2)证明:连接AC,∵AO=3,OC=,∴AC==2,∴AM=MC=AC=2,∴△AMC为等边三角形,∴∠ACM=60°. 又∵AP为⊙M的直径,∴∠ACP=90°,∴∠OCE=30°,设OE=x,则EC=2x. 在Rt△OEC中,x2+()2=(2x)2,解得x=1,∴OE=1,BE=2. ∴BE=2OE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级上册综合强化练6
【练习范围:24.1 满分:100分】
一、选择题(每小题4分,共32分)
1. 如图,点A、B、C都在☉O上,且点C在弦AB所对的优弧上,如果∠AOB=64°,那∠ACB的度数是( )
A.26° B.30° C.32° D.64°
2. 如图,在☉O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB B.CE=EO C.∠OCE=40° D.∠BOC=2∠BAD
3. 如图,A,B,C,D是☉O上的四点,且AD=BC,则AB与CD的大小关系为( )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
4. 如图,CD为☉O的直径,弦AB⊥CD,垂足为M,若AB=12.OM∶MD=5∶8,则☉O的周长为( )
A.26π B.13π C. D.
5. 如图,点A、B、C在☉O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
6. 如图,C,D是以线段AB为直径的☉O上两点,若CA=CD,且∠ACD=40°,则∠CAB等于( )
A.10° B.20° C.30° D.40°
7. 如图,☉O的半径是2,AB是☉O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( )
A.60° B.120° C.60°或120° D.30°或150°
8. 如图,AB是☉O的直径,C,D是☉O上的点,且OC∥BD,AD分别与BC,OC相交于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED. 其中一定成立的是( )
A.②④⑤⑥ B.①③⑤⑥ C.②③④⑥ D.①③④⑤
二、填空题(每小题4分,共24分)
9. 如图所示,☉O与☉O′是任意的两个圆,把这两个圆看作一个整体,它是一个轴对称图形,这个图形的对称轴是 .
10. 如图,△ABC内接于☉O,若∠OAB=32°,则∠C= .
11. 如图,AB为☉O的直径,C,D为☉O上的点,=.若∠CAB=40°,∠CAD= .
12. 如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 .
13. 如图,已知☉O的直径AB=6,E、F为AB的三等分点,M、N为上的两点,且∠MEB=∠NFB=60°,则EM+FN= .
14. 在半径为1的☉O中,弦AB,AC的长分别为1和2,则∠BAC的度数为 .
三、解答题(共44分)
15. (8分)如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥
AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE∶CD=5∶24.
(1)求CD的长;
(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满
16. (8分)如图,在☉O中,AB、CD为互相垂直的两条弦,垂足为点E.当☉O的半径为2,AB2+CD2=28,求OE的长.
17. (8分)如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆☉O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若☉O的直径为2,求PC2+PB2的值.
18. (10分)如图,AB是☉O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,则☉O的半径为 ,CE的长是 .
19. (10分)如图,在平面直角坐标系中,以点M(0,)为圆心,以2为半径作☉M交x轴于A、B两点,交y轴于C、D两点,连接AM并延长交☉M于P点,连接PC交x轴于点E.
(1)求点C、P的坐标;
(2)求证:BE=2OE.
参 考 答 案
一、选择题(每小题4分,共32分)
1. C 2. D 3. B 4. B 5. B 6. B 7. C 8. D
二、填空题(每小题4分,共24分)
9. 直线OO′
10. 58°
11. 25°
12. 5
13.
14. 15°或105°
三、解答题(共44分)
15. (8分)
解:(1)∵直径AB=26m,∴OD=AB=×26=13(m). ∵OE⊥CD,∴DE=CD. ∵OE∶CD=5∶24,∴OE∶ED=5∶12,∴设OE=5x,ED=12x. ∴在Rt△ODE中,(5x)2+(12x)2=132. 解得x=1. ∴CD=2DE=2×12×1=24(m).
(2)由(1)得OE=1×5=5(m),延长OE交圆O于点F,∴EF=OF-OE=13-5=8(m). ∴8÷4=2(小时),即经过2小时桥洞会刚刚被灌满.
16. (8分)
解:如图,过点O分别作OM⊥CD,ON⊥AB,垂足分别为M,N,连接OC,OB,∵AB⊥CD,OM⊥CD,ON⊥AB,∴四边形OMEN是矩形,∴ON=ME,OM=EN. 在Rt△COM中,OC2-CM2=OM2. 在Rt△BON中,OB2-BN2=ON2,而BN=AB,CM=CD,∴OE2=MO2+ON2=OC2-CM2+OB2-BN2=2OB2-(AB2+CD2),又∵⊙O的半径为2,AB2+CD2=28,∴OE2=8-7=1,即OE=1.
17. (8分)
(1)证明:∵△ABC是等腰直角三角形,∴AC=AB,∠CAB=90°,∠PBA=45°,∴∠PEA=∠PBA=45°. ∵PE为⊙O的直径,∴∠PAE=90°,∴∠APE=∠PEA=45°,∴△APE为等腰直角三角形;
(2)解:∵∠PAE=∠CAB=90°,∴∠CAB-∠PAB=∠PAE-∠PAB,∴∠CAP=∠BAE,∴△CAP≌△BAE(SAS),∴PC=BE. ∵∠PBE=90°,∴在Rt△PBE中,BE2+PB2=PE2=4. ∴PC2+PB2=4.
18. (10分)
(1)证明:∵AB为⊙O直径,∴∠ACB=90°,∴∠A+∠CBA=90°. 又CE⊥AB,∴∠ECB+∠CBA=90°,∴∠BCE=∠A,又=,∴∠A=∠CBD,∴∠ECB=∠DBC,∴CF=BF.
(2)半径为5,CE===4.8.
19. (10分)(1)解:连接PB,∵PA是⊙M的直径,∴∠PBA=90°,又∵MO⊥AB,∴PB∥MO,∴PB=2OM=2. 在Rt△ABP中,AP=4,PB=2,根据勾股定理,得AB=6,∴AO=OB=3. ∴P点坐标为(3,2).圆的半径MC=2,又OM=,所以OC=MC-OM=,则点C的坐标为(0,-).
(2)证明:连接AC,∵AO=3,OC=,∴AC==2,∴AM=MC=AC=2,∴△AMC为等边三角形,∴∠ACM=60°. 又∵AP为⊙M的直径,∴∠ACP=90°,∴∠OCE=30°,设OE=x,则EC=2x. 在Rt△OEC中,x2+()2=(2x)2,解得x=1,∴OE=1,BE=2. ∴BE=2OE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
