人教版数学九年级上册:23.1—23.3综合强化练(含答案)
文档属性
| 名称 | 人教版数学九年级上册:23.1—23.3综合强化练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 533.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册综合强化练5
【练习范围:23.1—23.3 满分:100分】
一、选择题(每小题4分,共32分)
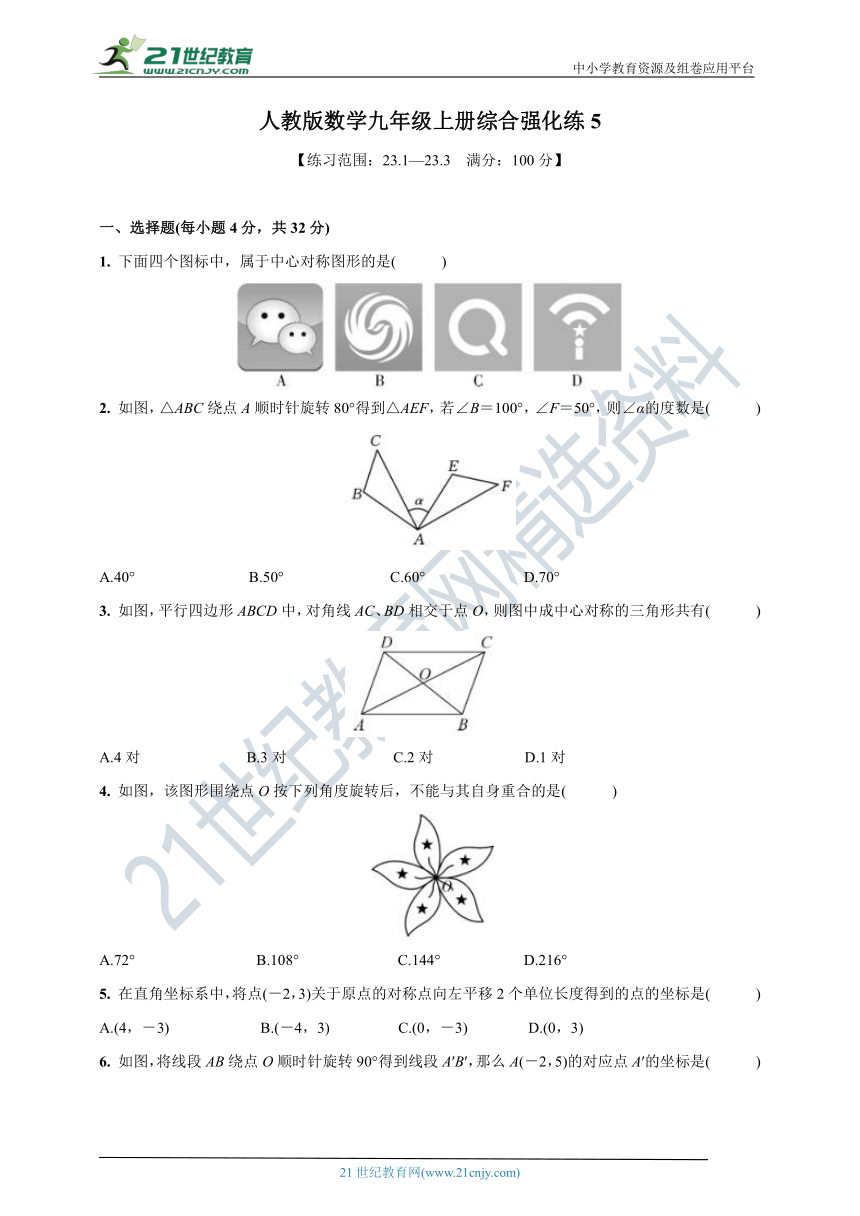
1. 下面四个图标中,属于中心对称图形的是( )
2. 如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=100°,∠F=50°,则∠α的度数是( )
A.40° B.50° C.60° D.70°
3. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,则图中成中心对称的三角形共有( )
A.4对 B.3对 C.2对 D.1对
4. 如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
5. 在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,-3) B.(-4,3) C.(0,-3) D.(0,3)
6. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
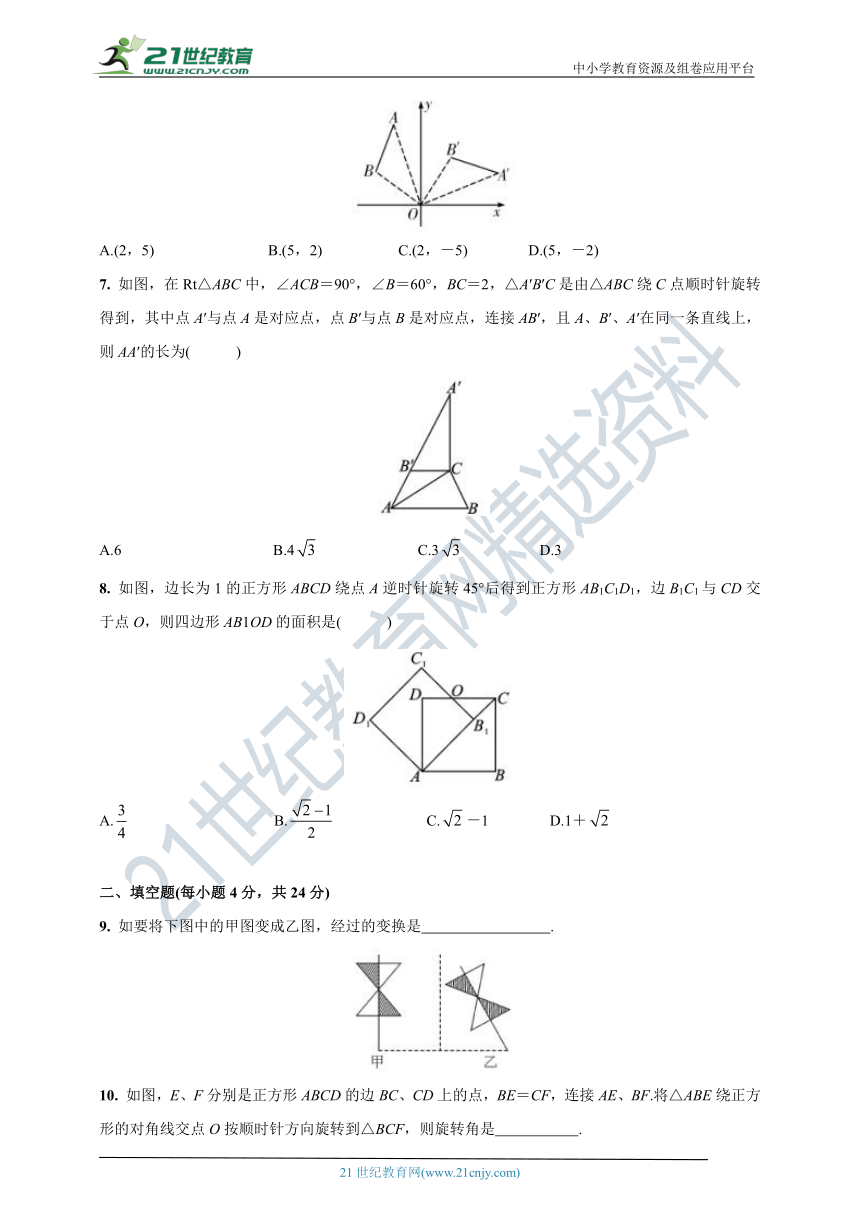
A.(2,5) B.(5,2) C.(2,-5) D.(5,-2)
7. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.6 B.4 C.3 D.3
8. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. B. C.-1 D.1+
二、填空题(每小题4分,共24分)
9. 如要将下图中的甲图变成乙图,经过的变换是 .
10. 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF,则旋转角是 .
11. 如图,正方形OEFG的一个顶点与正方形ABCD的对角线交点O重合,且正方形ABCD与正方形OEFG的边长都为2cm,则图中阴影部分的面积为 cm2.
12. 如图,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对(2,1)表示方格纸上点A的位置,用(1,2)表示点B的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是 .
13. 如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2).将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′,B′,C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′,B′,C′的对应点分别为A″,B″,C″,则点A″的坐标为 .
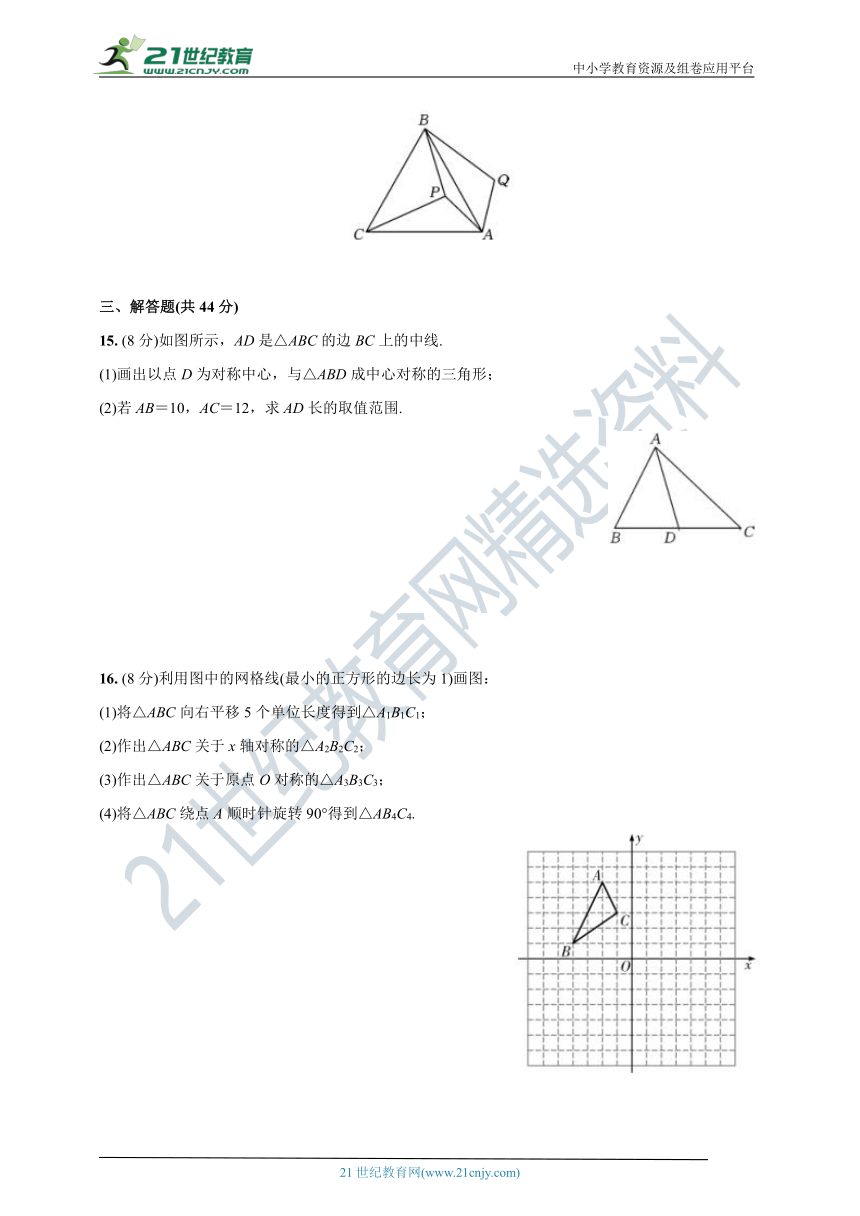
14. 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 .
三、解答题(共44分)
15. (8分)如图所示,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
16. (8分)利用图中的网格线(最小的正方形的边长为1)画图:
(1)将△ABC向右平移5个单位长度得到△A1B1C1;
(2)作出△ABC关于x轴对称的△A2B2C2;
(3)作出△ABC关于原点O对称的△A3B3C3;
(4)将△ABC绕点A顺时针旋转90°得到△AB4C4.
17. (8分)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
18. (10分)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
19. (10分)某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图1所示位置放置,现将Rt△AFE绕A点按逆时针方向旋转角α(0°<α<90°),如图2,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形 并说明理由.
参 考 答 案
一、选择题(每小题4分,共32分)
1. B 2. B 3. A 4. B 5. C 6. B 7. A 8. C
二、填空题(每小题4分,共24分)
9. 旋转、平移
10. 90°
11. 1
12. (5,2)
13. (6,0)
14. 24+9
三、解答题(共44分)
15. (8分)
解:(1)如图所示,△ECD即为所作.
(2)由中心对称可得EC=AB=10,且AD=DE,∴在△ACE中,2<AE<22,∴2<2AD<22,∴1<AD<11.
16. (8分)
解:(1)如图所示,△A1B1C1即为所作.
(2)如图所示,△A2B2C2即为所作.
(3)如图所示,△A3B3C3即为所作.
(4)如图所示,△AB4C4即为所作.
17. (8分)
解:(1)(0,2.5);
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
18. (10分)
(1)证明:由旋转的性质得DB=CB,∠ABD=∠EBC,∠ABE=60°. ∵AB⊥BC,∴∠ABC=90°,∴∠DBE=∠CBE=30°. 又∵BE=BE,∴△BDE≌△BCE(SAS).
(2)解:四边形ABED是菱形.
理由:由(1)知△BDE≌△BCE,由旋转知△BAD≌△BEC,∴BA=BE,AD=EC=DE. 又∵BE=CE,∴BA=BE=AD=DE,∴四边形ABED为菱形.
19. (10分)
(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,∴∠α=∠NAF.又∵∠B=∠F,AB=AF,∴△ABM≌△AFN(ASA).∴AM=AN.
(2)解:四边形ABPF是菱形.
理由:∵∠α=30°,∠EAF=90°,∴∠BAF=120°. 又∵∠B=∠F=60°,∴∠B+∠BAF=60°+120=180°,∠F+∠BAF=60°+120°=180°. ∴AF∥BC,AB∥EF. ∴四边形ABPF是平行四边形. 又∵AB=AF,∴四边形ABPF是菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级上册综合强化练5
【练习范围:23.1—23.3 满分:100分】
一、选择题(每小题4分,共32分)
1. 下面四个图标中,属于中心对称图形的是( )
2. 如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=100°,∠F=50°,则∠α的度数是( )
A.40° B.50° C.60° D.70°
3. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,则图中成中心对称的三角形共有( )
A.4对 B.3对 C.2对 D.1对
4. 如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
5. 在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,-3) B.(-4,3) C.(0,-3) D.(0,3)
6. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
A.(2,5) B.(5,2) C.(2,-5) D.(5,-2)
7. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.6 B.4 C.3 D.3
8. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. B. C.-1 D.1+
二、填空题(每小题4分,共24分)
9. 如要将下图中的甲图变成乙图,经过的变换是 .
10. 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF,则旋转角是 .
11. 如图,正方形OEFG的一个顶点与正方形ABCD的对角线交点O重合,且正方形ABCD与正方形OEFG的边长都为2cm,则图中阴影部分的面积为 cm2.
12. 如图,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对(2,1)表示方格纸上点A的位置,用(1,2)表示点B的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是 .
13. 如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2).将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′,B′,C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′,B′,C′的对应点分别为A″,B″,C″,则点A″的坐标为 .
14. 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 .
三、解答题(共44分)
15. (8分)如图所示,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
16. (8分)利用图中的网格线(最小的正方形的边长为1)画图:
(1)将△ABC向右平移5个单位长度得到△A1B1C1;
(2)作出△ABC关于x轴对称的△A2B2C2;
(3)作出△ABC关于原点O对称的△A3B3C3;
(4)将△ABC绕点A顺时针旋转90°得到△AB4C4.
17. (8分)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
18. (10分)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
19. (10分)某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图1所示位置放置,现将Rt△AFE绕A点按逆时针方向旋转角α(0°<α<90°),如图2,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形 并说明理由.
参 考 答 案
一、选择题(每小题4分,共32分)
1. B 2. B 3. A 4. B 5. C 6. B 7. A 8. C
二、填空题(每小题4分,共24分)
9. 旋转、平移
10. 90°
11. 1
12. (5,2)
13. (6,0)
14. 24+9
三、解答题(共44分)
15. (8分)
解:(1)如图所示,△ECD即为所作.
(2)由中心对称可得EC=AB=10,且AD=DE,∴在△ACE中,2<AE<22,∴2<2AD<22,∴1<AD<11.
16. (8分)
解:(1)如图所示,△A1B1C1即为所作.
(2)如图所示,△A2B2C2即为所作.
(3)如图所示,△A3B3C3即为所作.
(4)如图所示,△AB4C4即为所作.
17. (8分)
解:(1)(0,2.5);
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
18. (10分)
(1)证明:由旋转的性质得DB=CB,∠ABD=∠EBC,∠ABE=60°. ∵AB⊥BC,∴∠ABC=90°,∴∠DBE=∠CBE=30°. 又∵BE=BE,∴△BDE≌△BCE(SAS).
(2)解:四边形ABED是菱形.
理由:由(1)知△BDE≌△BCE,由旋转知△BAD≌△BEC,∴BA=BE,AD=EC=DE. 又∵BE=CE,∴BA=BE=AD=DE,∴四边形ABED为菱形.
19. (10分)
(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,∴∠α=∠NAF.又∵∠B=∠F,AB=AF,∴△ABM≌△AFN(ASA).∴AM=AN.
(2)解:四边形ABPF是菱形.
理由:∵∠α=30°,∠EAF=90°,∴∠BAF=120°. 又∵∠B=∠F=60°,∴∠B+∠BAF=60°+120=180°,∠F+∠BAF=60°+120°=180°. ∴AF∥BC,AB∥EF. ∴四边形ABPF是平行四边形. 又∵AB=AF,∴四边形ABPF是菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
