2022—2023学年苏科版数学八年级上册1.3探索全等三角形的条件 sss 课件(共38张PPT)
文档属性
| 名称 | 2022—2023学年苏科版数学八年级上册1.3探索全等三角形的条件 sss 课件(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 757.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 13:01:22 | ||
图片预览



文档简介
(共38张PPT)
1.3探索三角形全等的条件(6)
学习目标
1. 掌握三角形全等的“边边边”条件,了解三角形的稳定性.
2. 能够进行有条理的思考并进行推理与证明.
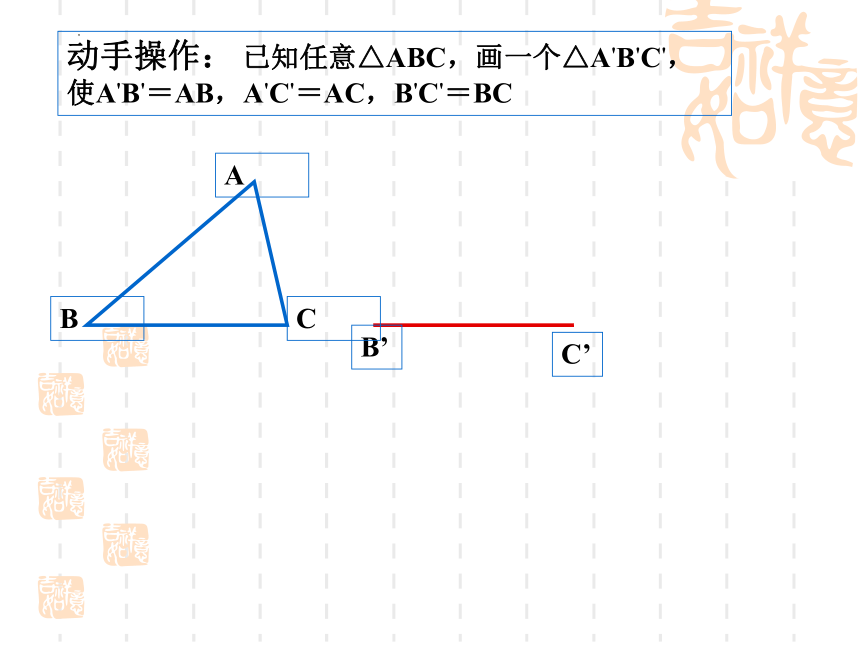
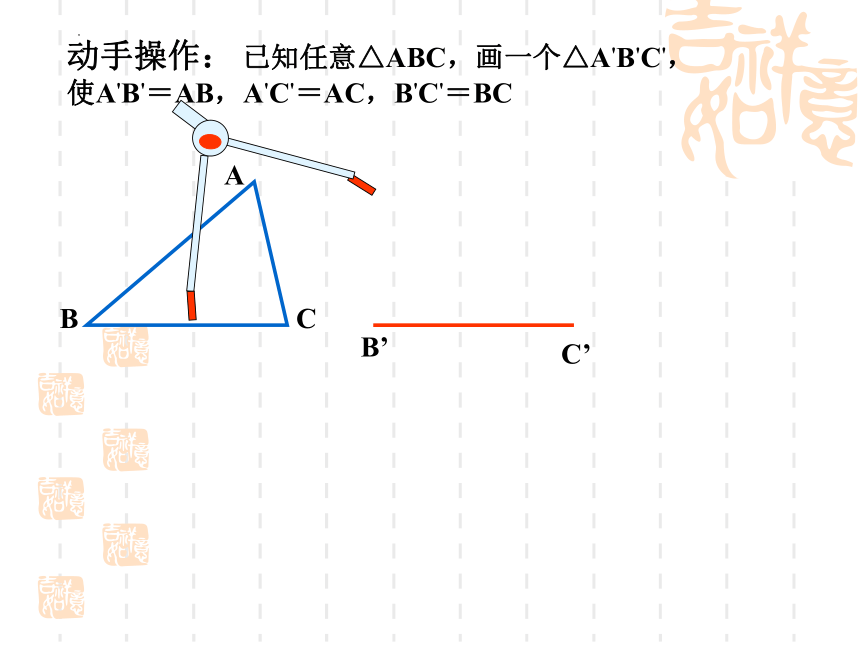
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
自主预习
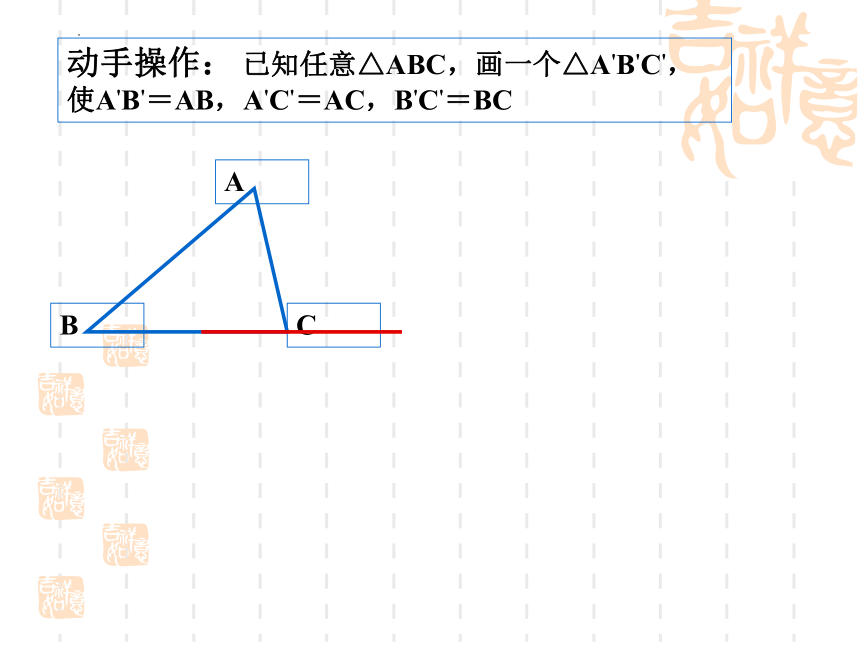
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
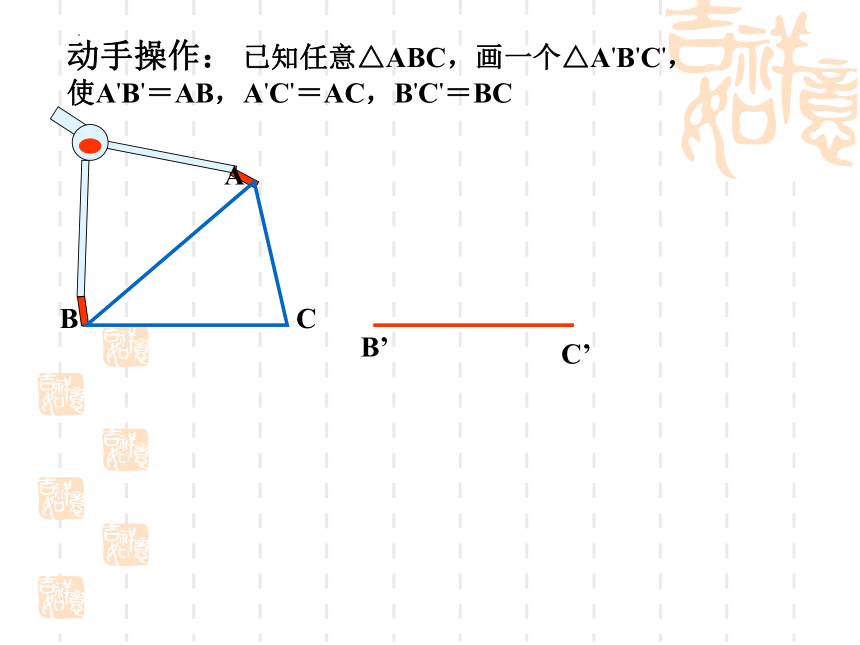
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
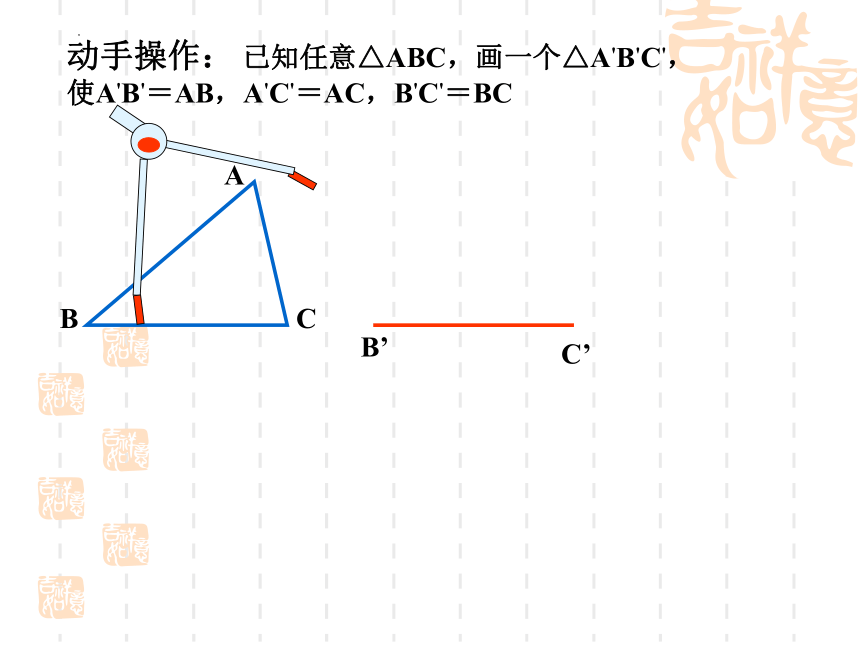
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
B’
C’
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
A’
画法:1、画线段B‘C'=BC 。
2、分别以B',C'为圆心,BA、CA为半径画弧,两弧相交于点A'。
3、连结A‘B'、A'C',得△A'B'C'。
剪下△A‘B’C‘,放在△ABC上,可以看到△A’B‘C’≌△ABC,由此可得判定两个三角形全等的又一个基本事实。
全等三角形判定(三)
如果一个三角形的三条边与另一个三角形的三条边对应相等,那么这两个三角形全等。
简称“边边边”,简记为SSS。
巩固练习一
木工师傅在做如图所示的门时,通常在门上角处斜钉两根木条,其中的道理是 .
三角形具有稳定性
已知:AB=AD,CB=CD 求证:AC平分 BAD
A
B
C
D
证明:在△ABC和△ADC中
AB=AD (已知)
CB=CD (已知)
AC=AC (公共边)
△ABC ≌ △ADC (SSS)
BAC= DAC(全等三角形的对应角相等)
即AC平分 BAD
如果连结BD,那么AC与BD有什么特殊关系吗?为什么?
合作探究
已知:在△ABC中,AB=AC,D是BC的中点。
求证: AD BC
A
B
C
D
分析:
D是BC的中点
BD=CD
AB=AC
AD=AD
△ADB △ADC
ADB= ADC
ADB与 ADC
是邻补角
ADB= ADC=90°
AD BC
解题
个性展示
≌
已知:在△ABC中,AB=AC,D是BC的中点。
求证: AD BC
A
B
C
D
证明: ∵ D是BC的中点(已知)
BD=CD(线段中点的定义)
在△ADB 和△ADC中
AB=AC,
BD=CD ,
AD=AD
△ADB △ADC(SSS)
∵ ADB= ADC(全等三角形对应角相等)
又∵ ADB与 ADC是邻补角
ADB= ADC=90°
AD BC(垂直的定义)
≌
整合提升
如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.求证:∠B=∠E.
1.为了判断三角形全等,我们可以寻找三组对应相等的边,运用“SSS”的全等条件来判定;
2.为了推出线段相等,应注意中点、公共边等条件.
课堂小结
1.判断
(1)判断两个三角形全等的条件中,至少要有一个角对应相等。 ( )
(2)有一组边对应相等的两个等边三角形全等 ( )
(3)两腰对应相等的两个三角形全等。 ( )
(4)底边和腰对应相等的两个等腰三角形全等。( )
检测反馈
2. (1)如图,AB=CD,AC=BD,△ABC和 △DCB是否全等?试说明理由.
解:在△ABC △DCB中,理由如下:
AB = CD
AC = BD
=
BC
BC
△ABC ( );
△DCB
SSS
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要△ABF≌△ECD,
还需要条件__________________.
BF=DC
或BD=FC
≌
≌
3.如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA;
(2)∠B=∠D.
B
A
C
D
1.3探索三角形全等的条件(6)
学习目标
1. 掌握三角形全等的“边边边”条件,了解三角形的稳定性.
2. 能够进行有条理的思考并进行推理与证明.
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
自主预习
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
B’
C’
A
B
C
B’
C’
动手操作: 已知任意△ABC,画一个△A'B'C',使A'B'=AB,A'C'=AC,B'C'=BC
A
B
C
A’
画法:1、画线段B‘C'=BC 。
2、分别以B',C'为圆心,BA、CA为半径画弧,两弧相交于点A'。
3、连结A‘B'、A'C',得△A'B'C'。
剪下△A‘B’C‘,放在△ABC上,可以看到△A’B‘C’≌△ABC,由此可得判定两个三角形全等的又一个基本事实。
全等三角形判定(三)
如果一个三角形的三条边与另一个三角形的三条边对应相等,那么这两个三角形全等。
简称“边边边”,简记为SSS。
巩固练习一
木工师傅在做如图所示的门时,通常在门上角处斜钉两根木条,其中的道理是 .
三角形具有稳定性
已知:AB=AD,CB=CD 求证:AC平分 BAD
A
B
C
D
证明:在△ABC和△ADC中
AB=AD (已知)
CB=CD (已知)
AC=AC (公共边)
△ABC ≌ △ADC (SSS)
BAC= DAC(全等三角形的对应角相等)
即AC平分 BAD
如果连结BD,那么AC与BD有什么特殊关系吗?为什么?
合作探究
已知:在△ABC中,AB=AC,D是BC的中点。
求证: AD BC
A
B
C
D
分析:
D是BC的中点
BD=CD
AB=AC
AD=AD
△ADB △ADC
ADB= ADC
ADB与 ADC
是邻补角
ADB= ADC=90°
AD BC
解题
个性展示
≌
已知:在△ABC中,AB=AC,D是BC的中点。
求证: AD BC
A
B
C
D
证明: ∵ D是BC的中点(已知)
BD=CD(线段中点的定义)
在△ADB 和△ADC中
AB=AC,
BD=CD ,
AD=AD
△ADB △ADC(SSS)
∵ ADB= ADC(全等三角形对应角相等)
又∵ ADB与 ADC是邻补角
ADB= ADC=90°
AD BC(垂直的定义)
≌
整合提升
如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.求证:∠B=∠E.
1.为了判断三角形全等,我们可以寻找三组对应相等的边,运用“SSS”的全等条件来判定;
2.为了推出线段相等,应注意中点、公共边等条件.
课堂小结
1.判断
(1)判断两个三角形全等的条件中,至少要有一个角对应相等。 ( )
(2)有一组边对应相等的两个等边三角形全等 ( )
(3)两腰对应相等的两个三角形全等。 ( )
(4)底边和腰对应相等的两个等腰三角形全等。( )
检测反馈
2. (1)如图,AB=CD,AC=BD,△ABC和 △DCB是否全等?试说明理由.
解:在△ABC △DCB中,理由如下:
AB = CD
AC = BD
=
BC
BC
△ABC ( );
△DCB
SSS
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要△ABF≌△ECD,
还需要条件__________________.
BF=DC
或BD=FC
≌
≌
3.如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA;
(2)∠B=∠D.
B
A
C
D
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
