2022-2023学年人教版数学九年级上册22.3实际问题与二次函数 课后培优(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册22.3实际问题与二次函数 课后培优(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 986.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:18:04 | ||
图片预览




文档简介
实际问题与二次函数(图形)
一、单选题
1.如图,抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内(含边界),且该抛物线经过原点O(0,0),则a的取值范围是( )
A.-2≤a≤-1 B. C. D.
2.如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线的一部分,则杯口的口径AC为( )
A.7 B.8 C.9 D.10
3.用总长为60 m的篱笆围成一个矩形场地,使矩形场地的一边靠墙,墙壁足够长,则围成的矩形场地的最大面积为( )
A.400 m2 B.450 m2 C.500 m2 D.900 m2
4.如图,抛物线y=2x2﹣8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=﹣x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
5.如图,在等边△ABC中,D、E分别是AB、AC上的动点,且,将△ADE沿着DE翻折,在D、E同时从A出发,分别向点B、C运动的过程中,与梯形BCED重合部分的面积( )
A.保持不变 B.先变大后变小 C.一直变大 D.先变小后变大
6.如图,现有一张透明网格(1000×1000)塑料片,纵向的网格线A1B1,…,A1000B1000,以A1为原点,A1A1000所在的直线为x轴建立平面直角坐标系,现有抛物线y=x2+x的一部分落在这个网格内,那么此抛物线在A20B20与A21B21之间(包括这两条网格线)与横向的网格线相交的点的个数为( )
A.20 B.38 C.40 D.42
7.在平面直角坐标系中,O为坐标原点.二次函数致的图象与x轴只有一个交点,且经过点,,则的面积为( )
A.8 B.12 C.16 D.4
8.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
9.如图,一个边长为的正方形,把它的边延长得到一个新的正方形,周长增加了,面积增加了.当x在一定范围内变化时,和,都随x的变化而变化,则与x,与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,一次函数关系 D.反比例函数关系,一次函数关系
10.如图,矩形中,,E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点,,连接,.甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.
甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
A.甲、乙都正确 B.甲、乙都不正确
C.甲正确,乙不正确 D.甲不正确,乙正确
11.已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
12.根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.某校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长5米),其它三面用防疫隔离材料搭建,但要开一扇1米宽的进出口(不需材料),共用防疫隔离材料10米搭建的隔离区的面积最大为( )平方米.
A. B.25 C. D.15
13.已知矩形MNPQ的顶点M,N,P,Q分别在正六边形ABCDEF的边DE,FA,AB,CD上,且.在点从移向(与不重合)的过程中,下列的判断中,正确的是( )
A.矩形MNPQ的面积与周长保持不变
B.矩形MNPQ的面积逐渐减小,周长逐渐增大
C.矩形MNPQ的面积与周长均逐渐增大
D.矩形MNPQ的面积与周长均逐渐减小
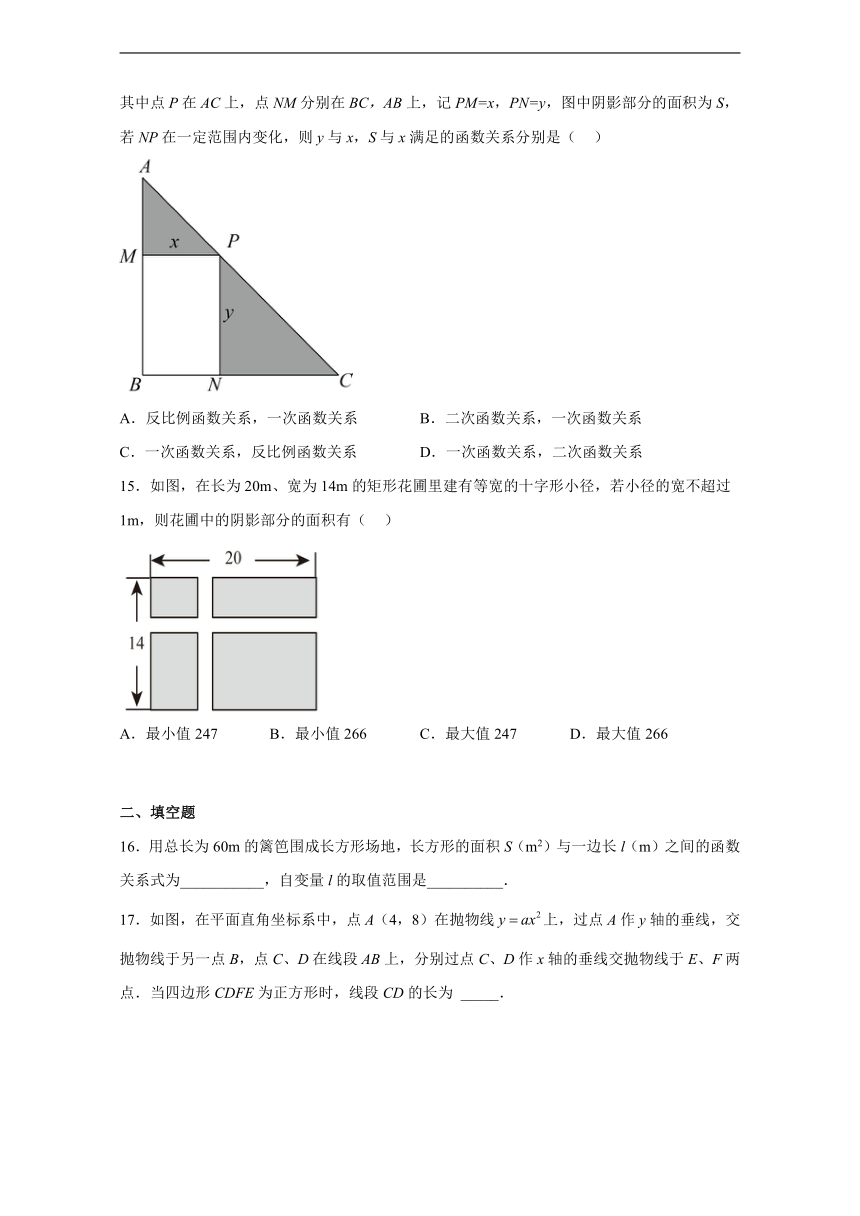
14.如图,某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN,其中点P在AC上,点NM分别在BC,AB上,记PM=x,PN=y,图中阴影部分的面积为S,若NP在一定范围内变化,则y与x,S与x满足的函数关系分别是( )
A.反比例函数关系,一次函数关系 B.二次函数关系,一次函数关系
C.一次函数关系,反比例函数关系 D.一次函数关系,二次函数关系
15.如图,在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1m,则花圃中的阴影部分的面积有( )
A.最小值247 B.最小值266 C.最大值247 D.最大值266
二、填空题
16.用总长为60m的篱笆围成长方形场地,长方形的面积S(m2)与一边长l(m)之间的函数关系式为___________,自变量l的取值范围是__________.
17.如图,在平面直角坐标系中,点A(4,8)在抛物线上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 _____.
18.一个玻璃杯竖直放置时的纵向截面如图1所示,其左右轮廓线,为同一抛物线的一部分,,都与水平地面平行,当杯子装满水后,,液体高度,将杯子绕倾斜倒出部分液体,当倾斜角时停止转动,如图2所示,此时液面宽度________,液面到点所在水平地面的距离是________.
19.如图,抛物线的顶点为,与轴交于点,轴,与抛物线交于点,轴,与射线交于点,,则_______.
20.如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为__________.
三、解答题
21.某庆典公司为迎接国庆共制作了A,B两种型号的庆典花车共100辆,已知制作A型花车的利润为20万元/辆,制作B型花车每辆的利润y(万元)与制作A型花车的数量x(辆)之间函数关系的图像如图所示.
(1)求y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)若该公司制作A,B两种花车的总利润为w(万元),试确定w与x之间的函数表达式,并求出x为何值时,总利润w有最大值,最大值是多少.
22.如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为y.
(1)求y与x的函数关系式,(不必写出自变量x的取值范围)
(2)写出此二次函数的二次项系数、一次项系数和常数项;
(3)写出次函数的图像的对称轴及顶点坐标.
23.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
24.如图,已知抛物线y=ax2+bx-8的图像与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
(1)求抛物线的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
25.南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“L”字形的墙面(粗线ABC表示墙面,已知AB⊥BC,AB=3米,BC=1米)和总长为11米的篱笆围建一个“日”字形的小型农场DBEF(细线表示篱笆,小型农场中间GH也是用篱笆隔开),点D可能在线段AB上(如图1),也可能在线段BA的延长线上(如图2),点E在线段BC的延长线上.
(1)当点D在线段AB上时,
①设DF的长为x米,请用含x的代数式表示EF的长;
②若要求所围成的小型农场DBEF的面积为9平方米,求DF的长;
(2)DF的长为多少米时,小型农场DBEF的面积最大?最大面积为多少平方米?
26.如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
(1)探究1:如果木板边长为2米,FC=1米,则一块木板用墙纸的费用需_____元;
(2)探究2:如果木板边长为1米,当FC的长为多少时,一块木板需用墙纸的费用最省?最省是多少元?
(3)探究3:设木板的边长为a(a为整数),当正方形EFCG的边长为多少时,墙纸费用最省?
参考答案:
1.D
解:根据图象可知:A(1,1),B(3,1),C(3,2),D(1,2).
当顶点在A,D之间时,图象经过点(0,0)和(2,0),
∴.
当x=1,,
解得;
当顶点在B,C之间时,图象经过点(0,0)和(6,0),
∴.
当x=3,,
解得.
∵顶点在矩形ABCD内,
∴.
故选:D.
2.C
解:当y=14时,,
解得,,
∴A(,14),C(,14),
∴AC=.
故选:C.
3.B
解:如图所示:
设AB=xm,
∵AB+CD+BC=60 m,且AB=CD,
∴BC=60﹣2x(m),
则S=x(60﹣2x)=﹣2x2+60x=﹣2(x﹣15)2+450,
∵60﹣2x>0,
∴x<30,
∵﹣2<0,
∴当x=15时,S取得最大值450,
故选:B.
4.B
解:由y=2x2﹣8x+6可知,令y=0,即2x2﹣8x+6=0,
解得x=1或3,
∴A(1,0),B(3,0),
由于将C1向右平移两个单位得到C2,
则C2的解析式为y=2(x﹣2)2﹣8(x﹣2)+6(3≤x≤5),
由图象知当直线y=﹣x+m在过B和与C2相切之间时与两个抛物线有三个不同的交点,
∴①当y=﹣x+m与C2相切时,
令y=﹣x+m=2(x﹣2)2﹣8(x﹣2)+6,
即2x2﹣15x+30﹣m=0,
∴△=8m﹣15=0,解得m=,
②当y=﹣x+m'过点B时,
即0=﹣3+m',解得m'=3,
综上,当时,直线y=﹣x+m与C1、C2共有3个不同的交点,
故选B.
5.B
解:设△ABC的边长为a,AD=x,与梯形BCED重合部分的面积为y,
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∵,
∴∠ADE=∠B=∠AED=∠C=60°,
∴△ADE是等边三角形,
∴DE=AD=x,
如图甲所示,当时,,
过点A作AG⊥DE于点G,
∵AG⊥DE,
∴∠AGD=90°,∠DAG=30°,,
∴,
∴,
∵,且x>0,
∴y随x的增大而增大,
当时,y最大,
如图乙所示,当时,设BC分别交DF,EF于点M,N,过点M作MG⊥DE于点G,
∵△ADE是等边三角形,
∴是等边三角形,
∴,
∴∠BDM=∠B=60°,
∴∠BMD=60°,
∴△BDM是等边三角形,
∵,
∴GM⊥BC,
∴∠BMG=90°,
∴∠DMG=30°,
∵AD=x,
∴BD=DM=a-x,
同理CN= a-x,
∴MN=a-(a-x+a-x)=2x-a,
∴,
∴,
∴,
∵,
∴当时,y有最大值,
∴与梯形BCED重合部分的面积先变大后变小.
故选:B
图甲 图乙
6.C
解:∵A1为原点,
∴A20对应的x=19,A21对应的x=20,
当x=19时,y1380,
当x=20时,y2,
∴y2﹣y1=40,
∴此抛物线在A20B20与A21B21之间与横向的网格线相交的点的个数为40个,
故选:C.
7.A
解:∵二次函数经过点,,
∴二次函数的对称轴为,
∴,即,
又∵二次函数的图象与x轴只有一个交点,
∴,即,
解得:,
∴二次函数解析式为,
令,解得:或4,
∴,或,,
∴,
故选:A.
8.C
解:方案1,设米,则米,
则菜园的面积
当时,此时散架的最大面积为8平方米;
方案2,当∠时,菜园最大面积平方米;
方案3,半圆的半径
此时菜园最大面积平方米>8平方米,
故选:C
9.A
解:由题意得:y1=4(8+x)﹣4×8=4x,此函数是一次函数;
y2=(8+x)2﹣82=x2+16x,此函数是二次函数,
故选:A.
10.D
解:∵四边形ABCD是矩形,
∴,∠ADC=∠C=90°,AB=CD,
∴∠ODE=∠OBF,∠OED=∠OFB,
∵O是BD的中点,
∴OB=OD,
∴△EOD≌△FOB(AAS),
∴DE=BF,
∴AE=CF,
又∵AE=DG,
∴CF=DG,
假设存在点E使得EG⊥FG,
∴∠EGF=90°,
∴∠EGD+∠CGF=90°,
又∵∠EGD+∠DEG=90°,
∴∠DEG=∠CGF,
又∵∠EDG=∠GCF=90°,
∴△EDG≌△GCF(AAS),
∴DE=CG,
∴AE+DE=DG+CG,即AD=CD,
∵,
∴CD>AD,与AD=CD矛盾,
∴假设不成立,即不存在点E使得EG与GF垂直,故甲说法错误;
设AB=CD=4,BC=AD=3,AE=DG=CF=x,则BF=DE=3-x,CG=4-x,
∴
,
即当时,△EFG的面积有最小值,
同理假设AB=CD=4时,只要满足BC<AB,都能求出△EFG的面积关于线段AE的长的二次函数关系式,即可求出△EFG的面积有最小值,故乙说法正确;
故选D.
11.D
解:如图:
连接AC,BD交于点O,AC分别交PQ,MN于点E,F.
∵菱形ABCD中,AB=6,∠B=60°,
∴△ABC是等边三角形,∠ABD=30°,
∴AC=AB=6.
∵矩形MNQP,
∴PQ∥BD,PM=EF,PQ⊥AC.
∴∠APE=∠ABD=30°,
设AP=a,AE=CFa,
∴EF=PM=6﹣a.
由勾股定理得:PE.
∴PQ=2PEa.
∴S矩形PMNQ=PM PQa×(6﹣a)(﹣a2+6a)
(a﹣3)2+9.
∵0,
∴当a=3时,矩形面积有最大值9.
故选:D.
12.C
解:设这个隔离区一边AB长为x米,则另一边BC长为(10-x+1)米,
依题意,隔离区的面积为S=x (10-x+1)=-x2+x=-(x-)2+,
∵-<0,
∴当x=时,隔离区有最大面积,最大面积为平方米,
故选:C.
13.D
解:正六边形为轴对称图形,以EF之间的对称轴为y轴,以直线AD上的对称轴为x轴,建立平面直角坐标系.
设六边形的边长为2,
则,,
设直线ED的解析式为y=kx+b,
解得,
故ED的解析式为,
点M在线段ED上,故设M(x,y),
矩形NMQP中,N与M关于y轴对称,∴N(-x,y),
Q与M关于x轴对称,∴Q(x,-y),
∴,,
∴ 矩形的周长C=2(NM+MQ)=2(2x+2y)= =,
由于,故C的值会随x的增大而减小,点M从E移动到D的过程中,x不断增大,所以周长会不断减小;
矩形的面积
∵<0,抛物线开后向下,当x>1时,S随x的增大而减小,所以面积也会逐渐减小.
故选:D.
14.D
解:设AB=m(m为常数).在△AMP中,∠A=45°,AM⊥PM,
∴△AMP为等腰直角三角形,
∴AM=PM,
又∵在矩形PMBN中,PN=BM,
∴x+y=PM+PN=AM+BM=AB=m,即y=﹣x+m,
∴y与x成一次函数关系,
∴S=S△ABC-S矩形PMBN=m2-xy=m2-x(﹣x+m)=x 2-mx+,
∴S与x成二次函数关系.
故选D.
15.A
解:设小径的宽为xm,阴影部分的面积为ym2
由题意得,y=(20 x)(14 x)=x2 34x+280=(x-17)2-9(0有最小值,对称轴为直线x=17,在对称轴的左侧,y随x的增大而减小
当x=1时,y有最小值,最小值为:y= (1-17)2-9=247
故选:A
16. 0<l<30
解:长方形一边长为l(m),则另一边长为(﹣l)m=(30﹣l)m,所以长方形的面积=l(30﹣l),
即S=﹣l2+30l,
l的范围为:0<l<30m.
故答案为:S=﹣l2+30l,0<l<30.
17.
解:把A(4,8)代入中得8=16a,
解得a=,
∴,
设点C横坐标为m,则CD=CE=2m,
∴点E坐标为(m,8﹣2m),
∴=8﹣2m,
解得m=(舍)或m=,
∴CD=2m=,
故答案为:.
18.
解:依题意建立如图平面直角坐标系,作∠ABE=45°,交抛物线于E,交x轴于F点,过B作于M点,
依题意得:,BM=12,
设抛物线的解析式为:
把A、B、C点坐标代入得:
∴
∴
∴
∵
∴
∵
∴
∴
∵
∴
设直线BF的解析式为:
把B、M点坐标代入得:
∴
∴
∵
∴
∴
∵
∴
∴
∵
∴
又∵
∴
∴
∴C到点BE的距离为:
故图2中液面到点所在水平地面的距离是
故答案为: ,
19.
解:把x=0代入y=x2-2x+m得y=m,
∴点B坐标为(0,m),
∵y=x2-2x+m=(x-1)2+m-1,
∴抛物线对称轴为直线x=1,顶点A坐标为(1,m-1),
∴点C坐标为(2,m),
∵CD∥y轴,OC=OD,
∴点D坐标为(2,-m),
∵点A横坐标为1,点D横坐标为2,
∴点A为OD中点,
∴2(m-1)=-m,
解得m=.
故答案为:.
20.或1.5
解:∵四边形ABCD是正方形,
∴∠CDE=90°,
设,则,
过点D作 PQ∥EF交CE于Q,GF于P,
∵四边形CEFG是正方形,
∴∠QEF=∠EFP=90°,EF=EC=FG,
∴∠EQP=90°,
∴四边形EQPF是矩形,
∴EC=EF=PQ,
∴
,
,
当时,面积的最小值为,
故答案为:.
21.(1)y=2x﹣50
(2),当x=67或68时总利润w有最大值,最大值是4112万元
(1)
解:设y与x之间的函数表达式为y=kx+b(k≠0),
根据题意得: ,
解得:,
∴y与x之间的函数表达式为y=2x﹣50;
(2)
由题意得:w=20x+(100﹣x)(2x﹣50)=+270x﹣5000=﹣2+4112.5,
∵﹣2<0,
∴抛物线开口向下,
又∵x为整数,
∴当x=67或68时,w最大,最大值为4112,
∴当x=67或68时总利润w有最大值,最大值是4112万元.
22.(1)y=-+15x(0<x≤18),
(2)二次项系数为,一次项系数为15,常数项为0
(3)对称轴x=15;及顶点坐标(15,)
(1)
解:依题意得,矩形的另一边长为,
则y=x=,
由图形可得,自变量x的取值范围是0<x≤18,
∴y与x的函数关系式为y=(0<x≤18);
(2)
解:∵y与x的函数关系式为y=,
∴二次项系数为,一次项系数为15,常数项为0;
(3)
解:y=,
∴对称轴:直线x=15;及顶点坐标(15,) .
23.(1);
(2)它能通过该隧道;
(3)货运卡车不能通过.
(1)
解:∵OE为线段BC的中垂线,
∴.
∵四边形ABCD是矩形,
∴AD=BC=8m,AB=CD=2m,
∴OC=4.
∴D(4,2,).E(0,6).
设抛物线的解析式为y=ax2+c,由题意,得
,
解得:
,
∴;
(2)
由题意,得
当y=4.4时,,
解得:,
∴宽度为:,
∴它能通过该隧道;
(3)
据题意,x=-0.2-2.4=-2.6m或x=0.2+2.4=2.6m,
把x=±2.6代入解析式,
得y=4.31m.
∵4.31m<4.4m,
∴货运卡车不能通过.
24.(1)抛物线解析式为y=+3x﹣8;
(2)点F的坐标是F(﹣4,﹣12);
(3)存在,点Q有坐标为(0,4)或(0,﹣4)或(0,﹣4)或(0,0).
(1)
解:将A(2,0),B(﹣8,0)C(0,﹣8)代入函数y=+bx+c,
得,
解得,,
∴抛物线解析式为y=+3x﹣8;
(2)
如图1中,
作FNy轴交BC于N,
设直线BC的解析式为=kx+b,
将B(﹣8,0)、C(0,-8)代入解析式得:
,
解得:
∴=﹣x﹣8,
设F(m,+3m﹣8),则N(m,﹣m﹣8),
∴
=FN×BO
=FN×8
=4FN
=4[(﹣m﹣8)﹣(+3m﹣8)]
=﹣2﹣16m
=﹣2+32,
∴当m=﹣4时,△FBC的面积有最大值,
此时F(﹣4,﹣12),
∴点F的坐标是F(﹣4,﹣12);
(3)
存在点Q(0,m),使得△BFQ为等腰三角形,理由如下:
①如图2﹣1,
当BQ=BF时,
由题意可列,
解得,=,=
∴(0,),(0,);
②如图2﹣2,
当QB=QF时,
由题意可列,
解题,m=﹣4,
∴(0,﹣4);
③如图2﹣3,
当FB=FQ时,
由题意可列,
解得,=0,=﹣24,
∴(0,0),(0,﹣24);
设直线BF的解析式为y=kx+b,
将B(﹣8,0),F(﹣4,﹣12)代入,
得,
解得,k=﹣3,b=﹣24,
∴=﹣3x﹣24,
当x=0时,y=﹣24,
∴点B,F,Q重合,故舍去,
∴点Q有坐标为(0,4)或(0,﹣4)或(0,﹣4)或(0,0).
25.(1)①(12﹣3x)米;②3米
(2)饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米
(1)
解:①设DF的长为x米,
∵点D在线段AB上,
∴EF=11﹣2x﹣(x﹣1)=12﹣3x,
∵AB=3,
∴EF≤3,即12﹣3x≤3,
∴x≥3;
②设DF的长为x米,根据题意得:
x(12﹣3x)=9,
解得:x1=3,x2=1(此时点D不在线段AB上,舍去),
∴x=3,
答:饲养场的长DF为3米;
(2)
解:设饲养场DBEF的面积为S,DF的长为x米,
①点D在线段AB上,由(1)知此时x≥3,
则S=x(12﹣3x)=﹣3x2+12x=﹣3(x﹣2)2+12,
∵﹣3<0,抛物线对称轴是直线x=2,
∴在对称轴右侧,S随x的增大而减小,
∴x=3时,S有最大值,S最大值=﹣3×12+12=9;
②点D在线段BA的延长线上,此时x<3,
则,
∵,,
∴时,S有最大值,S最大值=,
∴时,S最大值=(平方米);
∵>9,
∴饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米.
答:饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米.
26.(1)220;
(2)当FC的长为m时,一块木板需用墙纸的费用最省,最省是55元;
(3)当正方形EFCG的边长为时,墙纸费用最省.
(1)
解:∵CF=1m,BC=2m,
∴BF=1m,
∴,=1,=4 1 1=2,
∴一块木板用墙纸的费用为:1×60+1×80+2×40=220(元),
故答案为:220;
(2)
设FC=xm,则BF=(1 x)m,总费用为y元,
∴,,=,
∴,
∴当x=时,=55元,
答:当FC的长为m时,一块木板需用墙纸的费用最省,最省是55元;
(3)
设FC=xm,则BF=(a x)m,总费用为y元,
∴,,=,
∴,
∴当x=时,y有最小值,即墙纸费用最省,
答:当正方形EFCG的边长为时,墙纸费用最省.
一、单选题
1.如图,抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内(含边界),且该抛物线经过原点O(0,0),则a的取值范围是( )
A.-2≤a≤-1 B. C. D.
2.如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线的一部分,则杯口的口径AC为( )
A.7 B.8 C.9 D.10
3.用总长为60 m的篱笆围成一个矩形场地,使矩形场地的一边靠墙,墙壁足够长,则围成的矩形场地的最大面积为( )
A.400 m2 B.450 m2 C.500 m2 D.900 m2
4.如图,抛物线y=2x2﹣8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=﹣x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
5.如图,在等边△ABC中,D、E分别是AB、AC上的动点,且,将△ADE沿着DE翻折,在D、E同时从A出发,分别向点B、C运动的过程中,与梯形BCED重合部分的面积( )
A.保持不变 B.先变大后变小 C.一直变大 D.先变小后变大
6.如图,现有一张透明网格(1000×1000)塑料片,纵向的网格线A1B1,…,A1000B1000,以A1为原点,A1A1000所在的直线为x轴建立平面直角坐标系,现有抛物线y=x2+x的一部分落在这个网格内,那么此抛物线在A20B20与A21B21之间(包括这两条网格线)与横向的网格线相交的点的个数为( )
A.20 B.38 C.40 D.42
7.在平面直角坐标系中,O为坐标原点.二次函数致的图象与x轴只有一个交点,且经过点,,则的面积为( )
A.8 B.12 C.16 D.4
8.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
9.如图,一个边长为的正方形,把它的边延长得到一个新的正方形,周长增加了,面积增加了.当x在一定范围内变化时,和,都随x的变化而变化,则与x,与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,一次函数关系 D.反比例函数关系,一次函数关系
10.如图,矩形中,,E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点,,连接,.甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.
甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
A.甲、乙都正确 B.甲、乙都不正确
C.甲正确,乙不正确 D.甲不正确,乙正确
11.已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
12.根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.某校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长5米),其它三面用防疫隔离材料搭建,但要开一扇1米宽的进出口(不需材料),共用防疫隔离材料10米搭建的隔离区的面积最大为( )平方米.
A. B.25 C. D.15
13.已知矩形MNPQ的顶点M,N,P,Q分别在正六边形ABCDEF的边DE,FA,AB,CD上,且.在点从移向(与不重合)的过程中,下列的判断中,正确的是( )
A.矩形MNPQ的面积与周长保持不变
B.矩形MNPQ的面积逐渐减小,周长逐渐增大
C.矩形MNPQ的面积与周长均逐渐增大
D.矩形MNPQ的面积与周长均逐渐减小
14.如图,某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN,其中点P在AC上,点NM分别在BC,AB上,记PM=x,PN=y,图中阴影部分的面积为S,若NP在一定范围内变化,则y与x,S与x满足的函数关系分别是( )
A.反比例函数关系,一次函数关系 B.二次函数关系,一次函数关系
C.一次函数关系,反比例函数关系 D.一次函数关系,二次函数关系
15.如图,在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1m,则花圃中的阴影部分的面积有( )
A.最小值247 B.最小值266 C.最大值247 D.最大值266
二、填空题
16.用总长为60m的篱笆围成长方形场地,长方形的面积S(m2)与一边长l(m)之间的函数关系式为___________,自变量l的取值范围是__________.
17.如图,在平面直角坐标系中,点A(4,8)在抛物线上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 _____.
18.一个玻璃杯竖直放置时的纵向截面如图1所示,其左右轮廓线,为同一抛物线的一部分,,都与水平地面平行,当杯子装满水后,,液体高度,将杯子绕倾斜倒出部分液体,当倾斜角时停止转动,如图2所示,此时液面宽度________,液面到点所在水平地面的距离是________.
19.如图,抛物线的顶点为,与轴交于点,轴,与抛物线交于点,轴,与射线交于点,,则_______.
20.如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为__________.
三、解答题
21.某庆典公司为迎接国庆共制作了A,B两种型号的庆典花车共100辆,已知制作A型花车的利润为20万元/辆,制作B型花车每辆的利润y(万元)与制作A型花车的数量x(辆)之间函数关系的图像如图所示.
(1)求y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)若该公司制作A,B两种花车的总利润为w(万元),试确定w与x之间的函数表达式,并求出x为何值时,总利润w有最大值,最大值是多少.
22.如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为y.
(1)求y与x的函数关系式,(不必写出自变量x的取值范围)
(2)写出此二次函数的二次项系数、一次项系数和常数项;
(3)写出次函数的图像的对称轴及顶点坐标.
23.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
24.如图,已知抛物线y=ax2+bx-8的图像与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
(1)求抛物线的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
25.南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“L”字形的墙面(粗线ABC表示墙面,已知AB⊥BC,AB=3米,BC=1米)和总长为11米的篱笆围建一个“日”字形的小型农场DBEF(细线表示篱笆,小型农场中间GH也是用篱笆隔开),点D可能在线段AB上(如图1),也可能在线段BA的延长线上(如图2),点E在线段BC的延长线上.
(1)当点D在线段AB上时,
①设DF的长为x米,请用含x的代数式表示EF的长;
②若要求所围成的小型农场DBEF的面积为9平方米,求DF的长;
(2)DF的长为多少米时,小型农场DBEF的面积最大?最大面积为多少平方米?
26.如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
(1)探究1:如果木板边长为2米,FC=1米,则一块木板用墙纸的费用需_____元;
(2)探究2:如果木板边长为1米,当FC的长为多少时,一块木板需用墙纸的费用最省?最省是多少元?
(3)探究3:设木板的边长为a(a为整数),当正方形EFCG的边长为多少时,墙纸费用最省?
参考答案:
1.D
解:根据图象可知:A(1,1),B(3,1),C(3,2),D(1,2).
当顶点在A,D之间时,图象经过点(0,0)和(2,0),
∴.
当x=1,,
解得;
当顶点在B,C之间时,图象经过点(0,0)和(6,0),
∴.
当x=3,,
解得.
∵顶点在矩形ABCD内,
∴.
故选:D.
2.C
解:当y=14时,,
解得,,
∴A(,14),C(,14),
∴AC=.
故选:C.
3.B
解:如图所示:
设AB=xm,
∵AB+CD+BC=60 m,且AB=CD,
∴BC=60﹣2x(m),
则S=x(60﹣2x)=﹣2x2+60x=﹣2(x﹣15)2+450,
∵60﹣2x>0,
∴x<30,
∵﹣2<0,
∴当x=15时,S取得最大值450,
故选:B.
4.B
解:由y=2x2﹣8x+6可知,令y=0,即2x2﹣8x+6=0,
解得x=1或3,
∴A(1,0),B(3,0),
由于将C1向右平移两个单位得到C2,
则C2的解析式为y=2(x﹣2)2﹣8(x﹣2)+6(3≤x≤5),
由图象知当直线y=﹣x+m在过B和与C2相切之间时与两个抛物线有三个不同的交点,
∴①当y=﹣x+m与C2相切时,
令y=﹣x+m=2(x﹣2)2﹣8(x﹣2)+6,
即2x2﹣15x+30﹣m=0,
∴△=8m﹣15=0,解得m=,
②当y=﹣x+m'过点B时,
即0=﹣3+m',解得m'=3,
综上,当时,直线y=﹣x+m与C1、C2共有3个不同的交点,
故选B.
5.B
解:设△ABC的边长为a,AD=x,与梯形BCED重合部分的面积为y,
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∵,
∴∠ADE=∠B=∠AED=∠C=60°,
∴△ADE是等边三角形,
∴DE=AD=x,
如图甲所示,当时,,
过点A作AG⊥DE于点G,
∵AG⊥DE,
∴∠AGD=90°,∠DAG=30°,,
∴,
∴,
∵,且x>0,
∴y随x的增大而增大,
当时,y最大,
如图乙所示,当时,设BC分别交DF,EF于点M,N,过点M作MG⊥DE于点G,
∵△ADE是等边三角形,
∴是等边三角形,
∴,
∴∠BDM=∠B=60°,
∴∠BMD=60°,
∴△BDM是等边三角形,
∵,
∴GM⊥BC,
∴∠BMG=90°,
∴∠DMG=30°,
∵AD=x,
∴BD=DM=a-x,
同理CN= a-x,
∴MN=a-(a-x+a-x)=2x-a,
∴,
∴,
∴,
∵,
∴当时,y有最大值,
∴与梯形BCED重合部分的面积先变大后变小.
故选:B
图甲 图乙
6.C
解:∵A1为原点,
∴A20对应的x=19,A21对应的x=20,
当x=19时,y1380,
当x=20时,y2,
∴y2﹣y1=40,
∴此抛物线在A20B20与A21B21之间与横向的网格线相交的点的个数为40个,
故选:C.
7.A
解:∵二次函数经过点,,
∴二次函数的对称轴为,
∴,即,
又∵二次函数的图象与x轴只有一个交点,
∴,即,
解得:,
∴二次函数解析式为,
令,解得:或4,
∴,或,,
∴,
故选:A.
8.C
解:方案1,设米,则米,
则菜园的面积
当时,此时散架的最大面积为8平方米;
方案2,当∠时,菜园最大面积平方米;
方案3,半圆的半径
此时菜园最大面积平方米>8平方米,
故选:C
9.A
解:由题意得:y1=4(8+x)﹣4×8=4x,此函数是一次函数;
y2=(8+x)2﹣82=x2+16x,此函数是二次函数,
故选:A.
10.D
解:∵四边形ABCD是矩形,
∴,∠ADC=∠C=90°,AB=CD,
∴∠ODE=∠OBF,∠OED=∠OFB,
∵O是BD的中点,
∴OB=OD,
∴△EOD≌△FOB(AAS),
∴DE=BF,
∴AE=CF,
又∵AE=DG,
∴CF=DG,
假设存在点E使得EG⊥FG,
∴∠EGF=90°,
∴∠EGD+∠CGF=90°,
又∵∠EGD+∠DEG=90°,
∴∠DEG=∠CGF,
又∵∠EDG=∠GCF=90°,
∴△EDG≌△GCF(AAS),
∴DE=CG,
∴AE+DE=DG+CG,即AD=CD,
∵,
∴CD>AD,与AD=CD矛盾,
∴假设不成立,即不存在点E使得EG与GF垂直,故甲说法错误;
设AB=CD=4,BC=AD=3,AE=DG=CF=x,则BF=DE=3-x,CG=4-x,
∴
,
即当时,△EFG的面积有最小值,
同理假设AB=CD=4时,只要满足BC<AB,都能求出△EFG的面积关于线段AE的长的二次函数关系式,即可求出△EFG的面积有最小值,故乙说法正确;
故选D.
11.D
解:如图:
连接AC,BD交于点O,AC分别交PQ,MN于点E,F.
∵菱形ABCD中,AB=6,∠B=60°,
∴△ABC是等边三角形,∠ABD=30°,
∴AC=AB=6.
∵矩形MNQP,
∴PQ∥BD,PM=EF,PQ⊥AC.
∴∠APE=∠ABD=30°,
设AP=a,AE=CFa,
∴EF=PM=6﹣a.
由勾股定理得:PE.
∴PQ=2PEa.
∴S矩形PMNQ=PM PQa×(6﹣a)(﹣a2+6a)
(a﹣3)2+9.
∵0,
∴当a=3时,矩形面积有最大值9.
故选:D.
12.C
解:设这个隔离区一边AB长为x米,则另一边BC长为(10-x+1)米,
依题意,隔离区的面积为S=x (10-x+1)=-x2+x=-(x-)2+,
∵-<0,
∴当x=时,隔离区有最大面积,最大面积为平方米,
故选:C.
13.D
解:正六边形为轴对称图形,以EF之间的对称轴为y轴,以直线AD上的对称轴为x轴,建立平面直角坐标系.
设六边形的边长为2,
则,,
设直线ED的解析式为y=kx+b,
解得,
故ED的解析式为,
点M在线段ED上,故设M(x,y),
矩形NMQP中,N与M关于y轴对称,∴N(-x,y),
Q与M关于x轴对称,∴Q(x,-y),
∴,,
∴ 矩形的周长C=2(NM+MQ)=2(2x+2y)= =,
由于,故C的值会随x的增大而减小,点M从E移动到D的过程中,x不断增大,所以周长会不断减小;
矩形的面积
∵<0,抛物线开后向下,当x>1时,S随x的增大而减小,所以面积也会逐渐减小.
故选:D.
14.D
解:设AB=m(m为常数).在△AMP中,∠A=45°,AM⊥PM,
∴△AMP为等腰直角三角形,
∴AM=PM,
又∵在矩形PMBN中,PN=BM,
∴x+y=PM+PN=AM+BM=AB=m,即y=﹣x+m,
∴y与x成一次函数关系,
∴S=S△ABC-S矩形PMBN=m2-xy=m2-x(﹣x+m)=x 2-mx+,
∴S与x成二次函数关系.
故选D.
15.A
解:设小径的宽为xm,阴影部分的面积为ym2
由题意得,y=(20 x)(14 x)=x2 34x+280=(x-17)2-9(0
当x=1时,y有最小值,最小值为:y= (1-17)2-9=247
故选:A
16. 0<l<30
解:长方形一边长为l(m),则另一边长为(﹣l)m=(30﹣l)m,所以长方形的面积=l(30﹣l),
即S=﹣l2+30l,
l的范围为:0<l<30m.
故答案为:S=﹣l2+30l,0<l<30.
17.
解:把A(4,8)代入中得8=16a,
解得a=,
∴,
设点C横坐标为m,则CD=CE=2m,
∴点E坐标为(m,8﹣2m),
∴=8﹣2m,
解得m=(舍)或m=,
∴CD=2m=,
故答案为:.
18.
解:依题意建立如图平面直角坐标系,作∠ABE=45°,交抛物线于E,交x轴于F点,过B作于M点,
依题意得:,BM=12,
设抛物线的解析式为:
把A、B、C点坐标代入得:
∴
∴
∴
∵
∴
∵
∴
∴
∵
∴
设直线BF的解析式为:
把B、M点坐标代入得:
∴
∴
∵
∴
∴
∵
∴
∴
∵
∴
又∵
∴
∴
∴C到点BE的距离为:
故图2中液面到点所在水平地面的距离是
故答案为: ,
19.
解:把x=0代入y=x2-2x+m得y=m,
∴点B坐标为(0,m),
∵y=x2-2x+m=(x-1)2+m-1,
∴抛物线对称轴为直线x=1,顶点A坐标为(1,m-1),
∴点C坐标为(2,m),
∵CD∥y轴,OC=OD,
∴点D坐标为(2,-m),
∵点A横坐标为1,点D横坐标为2,
∴点A为OD中点,
∴2(m-1)=-m,
解得m=.
故答案为:.
20.或1.5
解:∵四边形ABCD是正方形,
∴∠CDE=90°,
设,则,
过点D作 PQ∥EF交CE于Q,GF于P,
∵四边形CEFG是正方形,
∴∠QEF=∠EFP=90°,EF=EC=FG,
∴∠EQP=90°,
∴四边形EQPF是矩形,
∴EC=EF=PQ,
∴
,
,
当时,面积的最小值为,
故答案为:.
21.(1)y=2x﹣50
(2),当x=67或68时总利润w有最大值,最大值是4112万元
(1)
解:设y与x之间的函数表达式为y=kx+b(k≠0),
根据题意得: ,
解得:,
∴y与x之间的函数表达式为y=2x﹣50;
(2)
由题意得:w=20x+(100﹣x)(2x﹣50)=+270x﹣5000=﹣2+4112.5,
∵﹣2<0,
∴抛物线开口向下,
又∵x为整数,
∴当x=67或68时,w最大,最大值为4112,
∴当x=67或68时总利润w有最大值,最大值是4112万元.
22.(1)y=-+15x(0<x≤18),
(2)二次项系数为,一次项系数为15,常数项为0
(3)对称轴x=15;及顶点坐标(15,)
(1)
解:依题意得,矩形的另一边长为,
则y=x=,
由图形可得,自变量x的取值范围是0<x≤18,
∴y与x的函数关系式为y=(0<x≤18);
(2)
解:∵y与x的函数关系式为y=,
∴二次项系数为,一次项系数为15,常数项为0;
(3)
解:y=,
∴对称轴:直线x=15;及顶点坐标(15,) .
23.(1);
(2)它能通过该隧道;
(3)货运卡车不能通过.
(1)
解:∵OE为线段BC的中垂线,
∴.
∵四边形ABCD是矩形,
∴AD=BC=8m,AB=CD=2m,
∴OC=4.
∴D(4,2,).E(0,6).
设抛物线的解析式为y=ax2+c,由题意,得
,
解得:
,
∴;
(2)
由题意,得
当y=4.4时,,
解得:,
∴宽度为:,
∴它能通过该隧道;
(3)
据题意,x=-0.2-2.4=-2.6m或x=0.2+2.4=2.6m,
把x=±2.6代入解析式,
得y=4.31m.
∵4.31m<4.4m,
∴货运卡车不能通过.
24.(1)抛物线解析式为y=+3x﹣8;
(2)点F的坐标是F(﹣4,﹣12);
(3)存在,点Q有坐标为(0,4)或(0,﹣4)或(0,﹣4)或(0,0).
(1)
解:将A(2,0),B(﹣8,0)C(0,﹣8)代入函数y=+bx+c,
得,
解得,,
∴抛物线解析式为y=+3x﹣8;
(2)
如图1中,
作FNy轴交BC于N,
设直线BC的解析式为=kx+b,
将B(﹣8,0)、C(0,-8)代入解析式得:
,
解得:
∴=﹣x﹣8,
设F(m,+3m﹣8),则N(m,﹣m﹣8),
∴
=FN×BO
=FN×8
=4FN
=4[(﹣m﹣8)﹣(+3m﹣8)]
=﹣2﹣16m
=﹣2+32,
∴当m=﹣4时,△FBC的面积有最大值,
此时F(﹣4,﹣12),
∴点F的坐标是F(﹣4,﹣12);
(3)
存在点Q(0,m),使得△BFQ为等腰三角形,理由如下:
①如图2﹣1,
当BQ=BF时,
由题意可列,
解得,=,=
∴(0,),(0,);
②如图2﹣2,
当QB=QF时,
由题意可列,
解题,m=﹣4,
∴(0,﹣4);
③如图2﹣3,
当FB=FQ时,
由题意可列,
解得,=0,=﹣24,
∴(0,0),(0,﹣24);
设直线BF的解析式为y=kx+b,
将B(﹣8,0),F(﹣4,﹣12)代入,
得,
解得,k=﹣3,b=﹣24,
∴=﹣3x﹣24,
当x=0时,y=﹣24,
∴点B,F,Q重合,故舍去,
∴点Q有坐标为(0,4)或(0,﹣4)或(0,﹣4)或(0,0).
25.(1)①(12﹣3x)米;②3米
(2)饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米
(1)
解:①设DF的长为x米,
∵点D在线段AB上,
∴EF=11﹣2x﹣(x﹣1)=12﹣3x,
∵AB=3,
∴EF≤3,即12﹣3x≤3,
∴x≥3;
②设DF的长为x米,根据题意得:
x(12﹣3x)=9,
解得:x1=3,x2=1(此时点D不在线段AB上,舍去),
∴x=3,
答:饲养场的长DF为3米;
(2)
解:设饲养场DBEF的面积为S,DF的长为x米,
①点D在线段AB上,由(1)知此时x≥3,
则S=x(12﹣3x)=﹣3x2+12x=﹣3(x﹣2)2+12,
∵﹣3<0,抛物线对称轴是直线x=2,
∴在对称轴右侧,S随x的增大而减小,
∴x=3时,S有最大值,S最大值=﹣3×12+12=9;
②点D在线段BA的延长线上,此时x<3,
则,
∵,,
∴时,S有最大值,S最大值=,
∴时,S最大值=(平方米);
∵>9,
∴饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米.
答:饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米.
26.(1)220;
(2)当FC的长为m时,一块木板需用墙纸的费用最省,最省是55元;
(3)当正方形EFCG的边长为时,墙纸费用最省.
(1)
解:∵CF=1m,BC=2m,
∴BF=1m,
∴,=1,=4 1 1=2,
∴一块木板用墙纸的费用为:1×60+1×80+2×40=220(元),
故答案为:220;
(2)
设FC=xm,则BF=(1 x)m,总费用为y元,
∴,,=,
∴,
∴当x=时,=55元,
答:当FC的长为m时,一块木板需用墙纸的费用最省,最省是55元;
(3)
设FC=xm,则BF=(a x)m,总费用为y元,
∴,,=,
∴,
∴当x=时,y有最小值,即墙纸费用最省,
答:当正方形EFCG的边长为时,墙纸费用最省.
同课章节目录
