2022-2023学年鲁教版(五四制)九年级数学上册第一次阶段性(1.1—2.6)综合测试题(含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)九年级数学上册第一次阶段性(1.1—2.6)综合测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 365.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:18:24 | ||
图片预览



文档简介
2022-2023学年鲁教版九年级数学上册第一次阶段性(1.1—2.6)综合测试题(附答案)
一、单选题(36分)
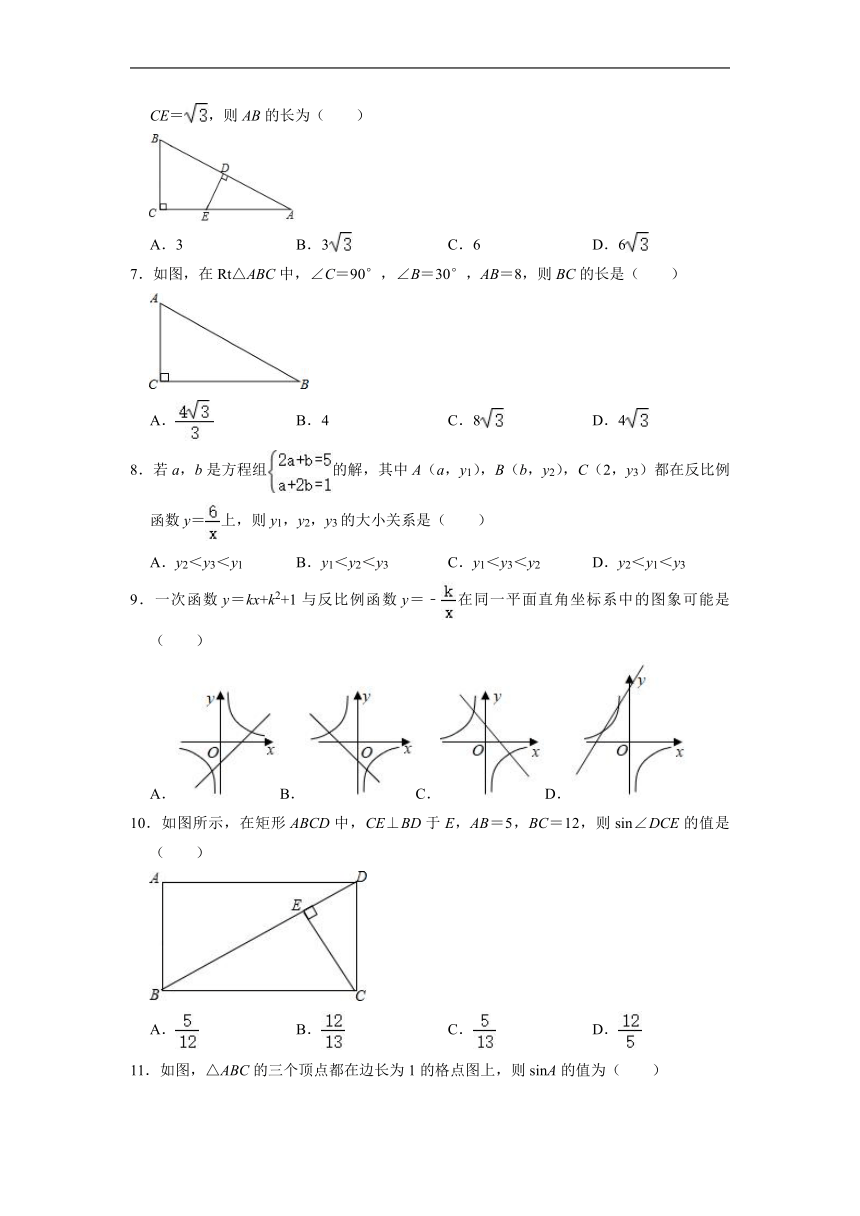
1.在Rt△ABC中,∠C=90°,sinA=,则tanA=( )
A. B. C. D.
2.反比例函数y=(k为常数,k≠0)的图象经过点(2,1),则下列说法错误的是( )
A.k=2
B.当x>0时,y 随x的增大而增大
C.函数图象分布在第一、三象限
D.当x<0时,y随x的增大而减小
3.若反比例函数y=(2m﹣1)的图象在第一、三象限,则m的值是( )
A.﹣1或1 B.小于的任意实数
C.1 D.不能确定
4.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,若OA2﹣AB2=6,则k的值为( )
A.6 B.3 C. D.
5.如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数的图象经过点C,且与AB交于点E.若OD=2,则△OCE的面积为( )
A.2 B.4 C.2 D.4
6.如图,在Rt△ABC中,∠C=90°,点D是AB的中点,DE⊥AB交AC于点E,DE=CE=,则AB的长为( )
A.3 B.3 C.6 D.6
7.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
8.若a,b是方程组的解,其中A(a,y1),B(b,y2),C(2,y3)都在反比例函数y=上,则y1,y2,y3的大小关系是( )
A.y2<y3<y1 B.y1<y2<y3 C.y1<y3<y2 D.y2<y1<y3
9.一次函数y=kx+k2+1与反比例函数y=﹣在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
10.如图所示,在矩形ABCD中,CE⊥BD于E,AB=5,BC=12,则sin∠DCE的值是( )
A. B. C. D.
11.如图,△ABC的三个顶点都在边长为1的格点图上,则sinA的值为( )
A. B. C. D.
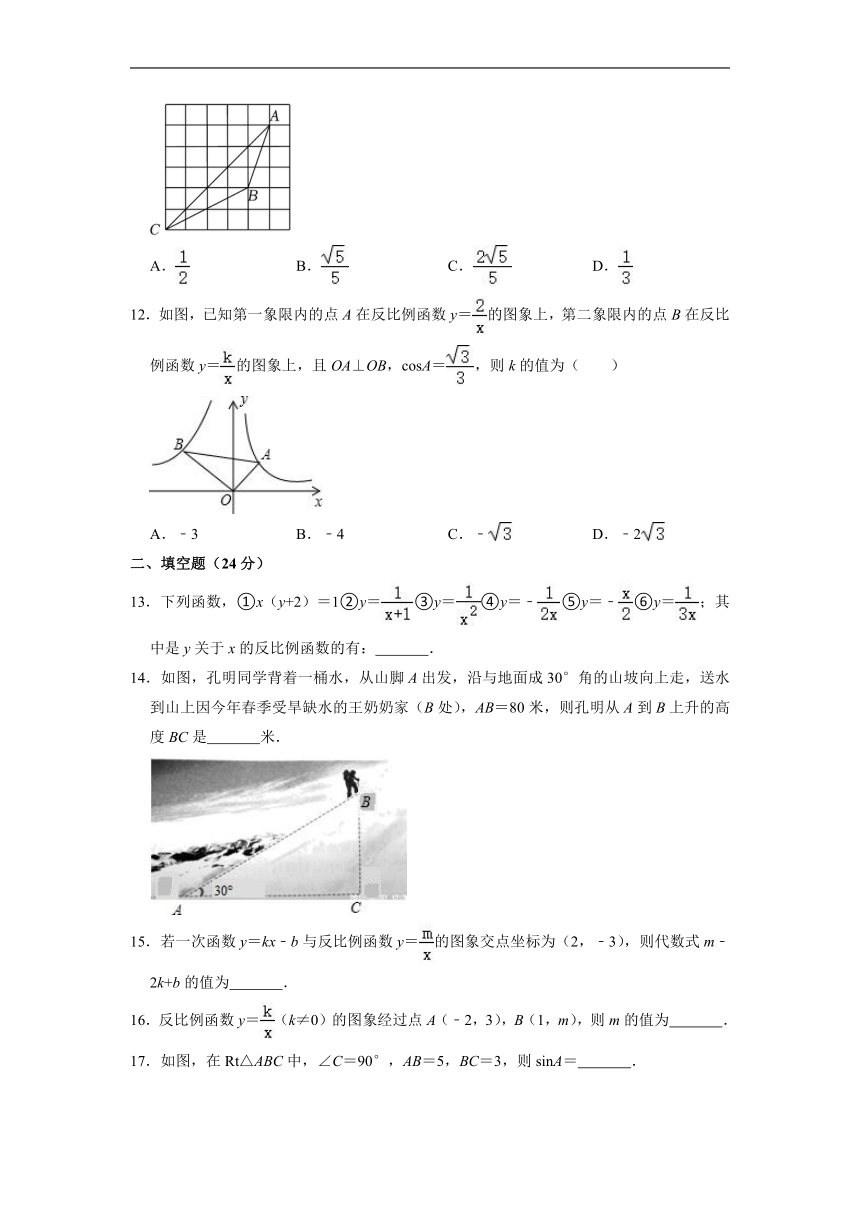
12.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=的图象上,且OA⊥OB,cosA=,则k的值为( )
A.﹣3 B.﹣4 C.﹣ D.﹣2
二、填空题(24分)
13.下列函数,①x(y+2)=1②y=③y=④y=﹣⑤y=﹣⑥y=;其中是y关于x的反比例函数的有: .
14.如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
15.若一次函数y=kx﹣b与反比例函数y=的图象交点坐标为(2,﹣3),则代数式m﹣2k+b的值为 .
16.反比例函数y=(k≠0)的图象经过点A(﹣2,3),B(1,m),则m的值为 .
17.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .
18.如图,点A在双曲线y=(x>0)上,点B在双曲线y=(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k= .
三、解答题(共60分)
19.计算
(1);
(2)(tan45°)2﹣;
(3)2cos45°﹣|﹣1|﹣()﹣2+(π﹣3)0.
20.如图,已知直线AB与x轴、y轴交于A、B两点与反比例函数的图象交于C点和D点,若OA=3,点C的横坐标为﹣3,tan∠BAO=.
(1)求反比例函数与一次函数的解析式;
(2)求△COD的面积;
(3)若一次函数的值大于反比例函数的值,求x的取值范围.
21.已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
22某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC的坡度为1:.
(1)求新坡面AC的坡角∠CAB;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
23.喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
24.如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计),观测得点在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米,问:
(1)分别求BC和AB多少米?
(2)小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(结果都保留根号)
25.如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:≈2.24,≈1.732,≈1.414)
参考答案
一、单选题(36分)
1.解:在Rt△ABC中,∠C=90°,sinA=,
∴sinA==,
∴设BC=4a,AB=5a,
∴AC===3a,
∴tanA===,
故选:B.
2.解:∵反比例函数y=(k为常数,k≠0)的图象经过点(2,1),
∴1=,
解得,k=2,故选项A说法正确;
∵k=2>0,
∴该函数的图象在第一、三象限,故选项C说法正确;
在每个象限内,y随x的增大而减小,故选项B说法错误、选项D说法正确;
故选:B.
3.解:根据题意得:,
解得:m=1.
故选:C.
4.解:由题意可知,OC=AC,DB=DA,OA=OC,AB=BD,
点B的横坐标为:OC+BD,纵坐标为OC﹣BD,
∵OA2﹣AB2=6,
∴OC2﹣DB2=3,即(OC+BD)(OC﹣BD)=3,
∴k=3,
故选:B.
5.解:连接AC,
∵OD=2,CD⊥x轴,
∴OD×CD=xy=4,
解得CD=2,由勾股定理,得OC==2,
由菱形的性质,可知OA=OC,
∵OC∥AB,
∵△OCE与△OAC同底等高,
∴S△OCE=S△OAC=×OA×CD=×2×2=2.
故选:C.
6.解:连接BE,
∵D是AB的中点,
∴BD=AD=AB
∵∠C=∠BDE=90°,
在Rt△BCE和Rt△BDE中,
∵,
∴△BCD≌△BDE,
∴BC=BD=AB.
∴∠A=30°.
∴tanA=
即=,
∴AD=3,
∴AB=2AD=6.
故选:C.
7.解:∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,
cosB=,
即cos30°=,
∴BC=8×=4;
故选:D.
8.解:方程组,解得,
∵点A(3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y=的图象上,
∴y1=2,y2=﹣6,y3=3,
∴y2<y1<y3,
故选:D.
9.解:∵一次函数y=kx+k2+1中,k2+1>0,
∴直线与y轴的交点在正半轴,故A、B不合题意,C、D符合题意,
C、由一次函数的图象过一、二、四象限可知k<0,由反比例函数的图象在二、四象限可知k>0,两结论相矛盾,故选项C错误;
D、由一次函数的图象过一、二、三象限可知k>0,由反比例函数的图象在二、四象限可知k>0,故选项D正确;
故选:D.
10.解:∵四边形ABCD是矩形,
∴CD=AB=5,∠BCD=90°,
∴BD==13,∠CBD+∠CDE=90°,
∵CE⊥BD,
∴∠CED=90°,
∴∠DCE+∠CDE=90°,
∴∠DCE=∠CBD,
∴sin∠DCE=sin∠CBD=;
故选:C.
11.解:如图,过点B作BD⊥AC于D.
由图可知,BD=,AB=.
∴sinA=.
故选:B.
12.解:过A作AE⊥x轴,过B作BF⊥x轴,
∵OA⊥OB,
∴∠AOB=90°,
∴∠BOF+∠EOA=90°,
∵∠BOF+∠FBO=90°,
∴∠EOA=∠FBO,
∵∠BFO=∠OEA=90°,
∴△BFO∽△OEA,
在Rt△AOB中,cos∠BAO==,
设AB=,则OA=1,根据勾股定理得:BO=,
∴OB:OA=:1,
∴S△BFO:S△OEA=2:1,
∵A在反比例函数y=上,
∴S△OEA=1,
∴S△BFO=2,
则k=﹣4.
故选:B.
二、填空题(24分)
13.解:①x(y+2)=1,可化为y=,不是反比例函数;
②y=,y与(x+1)成反比例关系;
③y= 是y关于x2的反比例函数;
④y=﹣符合反比例函数的定义,是反比例函数;
⑤y=﹣是正比例函数;
⑥y=符合反比例函数的定义,是反比例函数;
故答案为:④⑥.
14.解:在Rt△ABC中,
∠A=30°,AB=80米,
则BC=80×=40 米.
故答案为40米.
15.解:将点(2,﹣3)分别代入两个函数表达式得:﹣3=2k﹣b,m=﹣6,
故m﹣2k+b=﹣6+3=﹣3,
故答案为﹣3.
16.解:∵点A(﹣2,3)在反比例函数y=(k≠0)的图象上,
∴k=﹣2×3=﹣6.
∵点B(1,m)在反比例函数y=(k≠0)的图象上,
∴m=﹣=﹣6.
故答案为:﹣6.
17.解:∵∠C=90°,AB=5,BC=3,
∴sinA==,
故答案为:.
18.解:因为点A在双曲线y=(x>0)上,设A点坐标为(a,),
因为四边形OABC是菱形,且∠AOC=60°,
所以OA=2a,
可得B点坐标为(3a,),
可得:k=,
故答案为:
三、解答题(共60分)
19.解:(1)
=
=1;
(2)(tan45°)2﹣
=12﹣
=1﹣(1﹣)
=;
(3)2cos45°﹣|﹣1|﹣()﹣2+(π﹣3)0
=2×﹣(﹣1)﹣4+1
=﹣+1﹣4+1
=﹣2.
20.解:(1)在Rt△AOB中,tan∠BAO==,
∵OA=3,
∴OB=2,
∴B(0,2),A(3,0),(1分)
设直线AB解析式为y=kx+b,
由题意得,
∴
∴一次函数的解析式为y=﹣x+2,
∵点C在直线上,且横坐标为﹣3,
∴当x=﹣3时,y=4,
∴C(﹣3,4),
∴反比例函数解析式为y=﹣
(2)消y得x2﹣3x﹣18=0,
∴x1=﹣3,x2=6,
∴D(6,﹣2),(6分)
∴S△DOC=S△AOC+S△AOD=×3×4+×3×2=9(8分)
(3)∵一次函数的值大于反比例函数的值,
∴﹣x+2>﹣,解得x<﹣3或0≤x<6.(10分)
21.解:∵∠A=105°,∠B=30°.
∴∠C=45°.
过点A作AD⊥BC于点D,
∴∠ADB=∠ADC=90°
在Rt△ADC中,
∵∠ADC=90°,∠C=45°,AC=2.
∴∠DAC=∠C=45°.
∵sinC=,
∴AD=.
∴AD=CD=.
在Rt△ADB中,∠ADB=90°,∠B=30°.
∵AD=,
∴AB=2.
∴由勾股定理得:BD=.
∴BC=BD+CD=.
22.解:(1)∵新坡面的坡度为1:,
∴tan∠CAB==,
∴∠CAB=30°.
答:新坡面的坡角∠CAB为30°;
(2)文化墙PM不需要拆除.
作CD⊥AB于点D,则CD=6,
∵坡面BC的坡度为1:1,新坡面的坡度为1:,
∴BD=CD=6,AD=6,∴AB=AD﹣BD=6﹣6<8,
∴文化墙PM不需要拆除.
23.解:(1)停止加热时,设y=,
由题意得:50=,
解得:k=900,
∴y=,
当y=100时,解得:x=9,
∴C点坐标为(9,100),
∴B点坐标为(8,100),
当加热烧水时,设y=ax+20,
由题意得:100=8a+20,
解得:a=10,
∴当加热烧水,函数关系式为y=10x+20(0≤x≤8);
当停止加热,得y与x的函数关系式为y=100(8<x≤9);y=(9<x≤45);
(2)把y=80代入y=,得x=11.25,
因此从烧水开到泡茶需要等待3.25分钟.
24.解:(1)过点C作CD⊥AB交AB延长线于一点D,
根据题意得∠BAC=30°,∠BCA=15°,
故∠DBC=∠DCB=45°,
在Rt△ADC中,
∵AC=400米,∠BAC=30°,
∴CD=BD=200米,
∴BC=200米,AD=200米
∴AB=AD﹣BD=(200﹣200)米,
(2)三角形ABC的周长为400+200+(200﹣200)≈829米
小金沿三角形绿化区的周边小路跑一圈共跑了约829米.
25.解:由题意,可知∠BDE=30°,∠BAC=60°,四边形ACED是矩形,
∴DE=AC=27.
在Rt△DBE中,
tan∠BDE=,
∴=,
∴BE=9.
在Rt△ABC中,
tan∠BAC=,
∴=,
∴BC=27≈46.8,
AD=CE=27﹣9=18≈31.2.
答:大楼AD的高约31.2m,塔BC的高约46.8m.
一、单选题(36分)
1.在Rt△ABC中,∠C=90°,sinA=,则tanA=( )
A. B. C. D.
2.反比例函数y=(k为常数,k≠0)的图象经过点(2,1),则下列说法错误的是( )
A.k=2
B.当x>0时,y 随x的增大而增大
C.函数图象分布在第一、三象限
D.当x<0时,y随x的增大而减小
3.若反比例函数y=(2m﹣1)的图象在第一、三象限,则m的值是( )
A.﹣1或1 B.小于的任意实数
C.1 D.不能确定
4.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,若OA2﹣AB2=6,则k的值为( )
A.6 B.3 C. D.
5.如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数的图象经过点C,且与AB交于点E.若OD=2,则△OCE的面积为( )
A.2 B.4 C.2 D.4
6.如图,在Rt△ABC中,∠C=90°,点D是AB的中点,DE⊥AB交AC于点E,DE=CE=,则AB的长为( )
A.3 B.3 C.6 D.6
7.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
8.若a,b是方程组的解,其中A(a,y1),B(b,y2),C(2,y3)都在反比例函数y=上,则y1,y2,y3的大小关系是( )
A.y2<y3<y1 B.y1<y2<y3 C.y1<y3<y2 D.y2<y1<y3
9.一次函数y=kx+k2+1与反比例函数y=﹣在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
10.如图所示,在矩形ABCD中,CE⊥BD于E,AB=5,BC=12,则sin∠DCE的值是( )
A. B. C. D.
11.如图,△ABC的三个顶点都在边长为1的格点图上,则sinA的值为( )
A. B. C. D.
12.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=的图象上,且OA⊥OB,cosA=,则k的值为( )
A.﹣3 B.﹣4 C.﹣ D.﹣2
二、填空题(24分)
13.下列函数,①x(y+2)=1②y=③y=④y=﹣⑤y=﹣⑥y=;其中是y关于x的反比例函数的有: .
14.如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
15.若一次函数y=kx﹣b与反比例函数y=的图象交点坐标为(2,﹣3),则代数式m﹣2k+b的值为 .
16.反比例函数y=(k≠0)的图象经过点A(﹣2,3),B(1,m),则m的值为 .
17.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .
18.如图,点A在双曲线y=(x>0)上,点B在双曲线y=(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k= .
三、解答题(共60分)
19.计算
(1);
(2)(tan45°)2﹣;
(3)2cos45°﹣|﹣1|﹣()﹣2+(π﹣3)0.
20.如图,已知直线AB与x轴、y轴交于A、B两点与反比例函数的图象交于C点和D点,若OA=3,点C的横坐标为﹣3,tan∠BAO=.
(1)求反比例函数与一次函数的解析式;
(2)求△COD的面积;
(3)若一次函数的值大于反比例函数的值,求x的取值范围.
21.已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
22某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC的坡度为1:.
(1)求新坡面AC的坡角∠CAB;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
23.喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
24.如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计),观测得点在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米,问:
(1)分别求BC和AB多少米?
(2)小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(结果都保留根号)
25.如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:≈2.24,≈1.732,≈1.414)
参考答案
一、单选题(36分)
1.解:在Rt△ABC中,∠C=90°,sinA=,
∴sinA==,
∴设BC=4a,AB=5a,
∴AC===3a,
∴tanA===,
故选:B.
2.解:∵反比例函数y=(k为常数,k≠0)的图象经过点(2,1),
∴1=,
解得,k=2,故选项A说法正确;
∵k=2>0,
∴该函数的图象在第一、三象限,故选项C说法正确;
在每个象限内,y随x的增大而减小,故选项B说法错误、选项D说法正确;
故选:B.
3.解:根据题意得:,
解得:m=1.
故选:C.
4.解:由题意可知,OC=AC,DB=DA,OA=OC,AB=BD,
点B的横坐标为:OC+BD,纵坐标为OC﹣BD,
∵OA2﹣AB2=6,
∴OC2﹣DB2=3,即(OC+BD)(OC﹣BD)=3,
∴k=3,
故选:B.
5.解:连接AC,
∵OD=2,CD⊥x轴,
∴OD×CD=xy=4,
解得CD=2,由勾股定理,得OC==2,
由菱形的性质,可知OA=OC,
∵OC∥AB,
∵△OCE与△OAC同底等高,
∴S△OCE=S△OAC=×OA×CD=×2×2=2.
故选:C.
6.解:连接BE,
∵D是AB的中点,
∴BD=AD=AB
∵∠C=∠BDE=90°,
在Rt△BCE和Rt△BDE中,
∵,
∴△BCD≌△BDE,
∴BC=BD=AB.
∴∠A=30°.
∴tanA=
即=,
∴AD=3,
∴AB=2AD=6.
故选:C.
7.解:∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,
cosB=,
即cos30°=,
∴BC=8×=4;
故选:D.
8.解:方程组,解得,
∵点A(3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y=的图象上,
∴y1=2,y2=﹣6,y3=3,
∴y2<y1<y3,
故选:D.
9.解:∵一次函数y=kx+k2+1中,k2+1>0,
∴直线与y轴的交点在正半轴,故A、B不合题意,C、D符合题意,
C、由一次函数的图象过一、二、四象限可知k<0,由反比例函数的图象在二、四象限可知k>0,两结论相矛盾,故选项C错误;
D、由一次函数的图象过一、二、三象限可知k>0,由反比例函数的图象在二、四象限可知k>0,故选项D正确;
故选:D.
10.解:∵四边形ABCD是矩形,
∴CD=AB=5,∠BCD=90°,
∴BD==13,∠CBD+∠CDE=90°,
∵CE⊥BD,
∴∠CED=90°,
∴∠DCE+∠CDE=90°,
∴∠DCE=∠CBD,
∴sin∠DCE=sin∠CBD=;
故选:C.
11.解:如图,过点B作BD⊥AC于D.
由图可知,BD=,AB=.
∴sinA=.
故选:B.
12.解:过A作AE⊥x轴,过B作BF⊥x轴,
∵OA⊥OB,
∴∠AOB=90°,
∴∠BOF+∠EOA=90°,
∵∠BOF+∠FBO=90°,
∴∠EOA=∠FBO,
∵∠BFO=∠OEA=90°,
∴△BFO∽△OEA,
在Rt△AOB中,cos∠BAO==,
设AB=,则OA=1,根据勾股定理得:BO=,
∴OB:OA=:1,
∴S△BFO:S△OEA=2:1,
∵A在反比例函数y=上,
∴S△OEA=1,
∴S△BFO=2,
则k=﹣4.
故选:B.
二、填空题(24分)
13.解:①x(y+2)=1,可化为y=,不是反比例函数;
②y=,y与(x+1)成反比例关系;
③y= 是y关于x2的反比例函数;
④y=﹣符合反比例函数的定义,是反比例函数;
⑤y=﹣是正比例函数;
⑥y=符合反比例函数的定义,是反比例函数;
故答案为:④⑥.
14.解:在Rt△ABC中,
∠A=30°,AB=80米,
则BC=80×=40 米.
故答案为40米.
15.解:将点(2,﹣3)分别代入两个函数表达式得:﹣3=2k﹣b,m=﹣6,
故m﹣2k+b=﹣6+3=﹣3,
故答案为﹣3.
16.解:∵点A(﹣2,3)在反比例函数y=(k≠0)的图象上,
∴k=﹣2×3=﹣6.
∵点B(1,m)在反比例函数y=(k≠0)的图象上,
∴m=﹣=﹣6.
故答案为:﹣6.
17.解:∵∠C=90°,AB=5,BC=3,
∴sinA==,
故答案为:.
18.解:因为点A在双曲线y=(x>0)上,设A点坐标为(a,),
因为四边形OABC是菱形,且∠AOC=60°,
所以OA=2a,
可得B点坐标为(3a,),
可得:k=,
故答案为:
三、解答题(共60分)
19.解:(1)
=
=1;
(2)(tan45°)2﹣
=12﹣
=1﹣(1﹣)
=;
(3)2cos45°﹣|﹣1|﹣()﹣2+(π﹣3)0
=2×﹣(﹣1)﹣4+1
=﹣+1﹣4+1
=﹣2.
20.解:(1)在Rt△AOB中,tan∠BAO==,
∵OA=3,
∴OB=2,
∴B(0,2),A(3,0),(1分)
设直线AB解析式为y=kx+b,
由题意得,
∴
∴一次函数的解析式为y=﹣x+2,
∵点C在直线上,且横坐标为﹣3,
∴当x=﹣3时,y=4,
∴C(﹣3,4),
∴反比例函数解析式为y=﹣
(2)消y得x2﹣3x﹣18=0,
∴x1=﹣3,x2=6,
∴D(6,﹣2),(6分)
∴S△DOC=S△AOC+S△AOD=×3×4+×3×2=9(8分)
(3)∵一次函数的值大于反比例函数的值,
∴﹣x+2>﹣,解得x<﹣3或0≤x<6.(10分)
21.解:∵∠A=105°,∠B=30°.
∴∠C=45°.
过点A作AD⊥BC于点D,
∴∠ADB=∠ADC=90°
在Rt△ADC中,
∵∠ADC=90°,∠C=45°,AC=2.
∴∠DAC=∠C=45°.
∵sinC=,
∴AD=.
∴AD=CD=.
在Rt△ADB中,∠ADB=90°,∠B=30°.
∵AD=,
∴AB=2.
∴由勾股定理得:BD=.
∴BC=BD+CD=.
22.解:(1)∵新坡面的坡度为1:,
∴tan∠CAB==,
∴∠CAB=30°.
答:新坡面的坡角∠CAB为30°;
(2)文化墙PM不需要拆除.
作CD⊥AB于点D,则CD=6,
∵坡面BC的坡度为1:1,新坡面的坡度为1:,
∴BD=CD=6,AD=6,∴AB=AD﹣BD=6﹣6<8,
∴文化墙PM不需要拆除.
23.解:(1)停止加热时,设y=,
由题意得:50=,
解得:k=900,
∴y=,
当y=100时,解得:x=9,
∴C点坐标为(9,100),
∴B点坐标为(8,100),
当加热烧水时,设y=ax+20,
由题意得:100=8a+20,
解得:a=10,
∴当加热烧水,函数关系式为y=10x+20(0≤x≤8);
当停止加热,得y与x的函数关系式为y=100(8<x≤9);y=(9<x≤45);
(2)把y=80代入y=,得x=11.25,
因此从烧水开到泡茶需要等待3.25分钟.
24.解:(1)过点C作CD⊥AB交AB延长线于一点D,
根据题意得∠BAC=30°,∠BCA=15°,
故∠DBC=∠DCB=45°,
在Rt△ADC中,
∵AC=400米,∠BAC=30°,
∴CD=BD=200米,
∴BC=200米,AD=200米
∴AB=AD﹣BD=(200﹣200)米,
(2)三角形ABC的周长为400+200+(200﹣200)≈829米
小金沿三角形绿化区的周边小路跑一圈共跑了约829米.
25.解:由题意,可知∠BDE=30°,∠BAC=60°,四边形ACED是矩形,
∴DE=AC=27.
在Rt△DBE中,
tan∠BDE=,
∴=,
∴BE=9.
在Rt△ABC中,
tan∠BAC=,
∴=,
∴BC=27≈46.8,
AD=CE=27﹣9=18≈31.2.
答:大楼AD的高约31.2m,塔BC的高约46.8m.
