2022-2023学年人教版数学九年级上册22.3实际问题与二次函数 课后提升 (含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册22.3实际问题与二次函数 课后提升 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:18:52 | ||
图片预览

文档简介
实际问题与二次函数(图形运动)
一、单选题
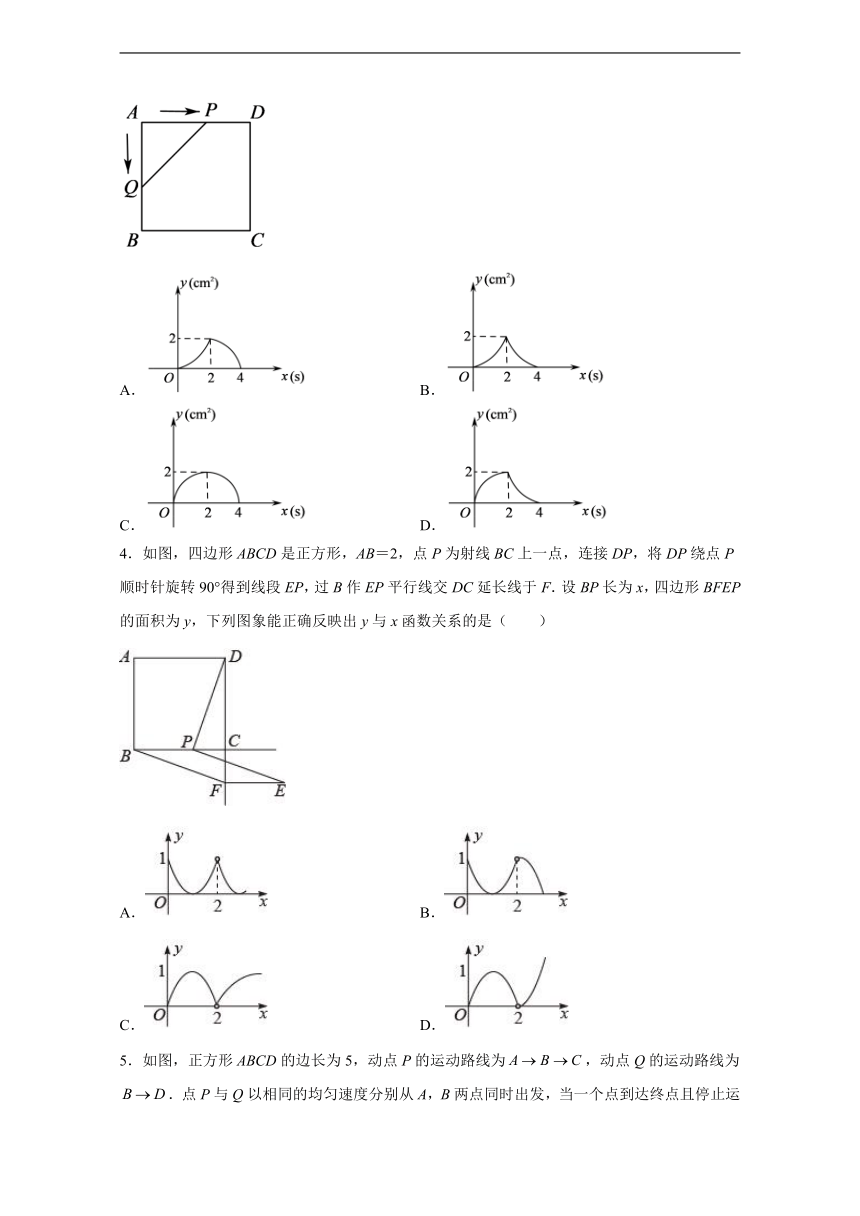
1.如图,在Rt△ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,则S关于t的函数图象大致为( )
A. B.
C. D.
2.如图,是等腰直角三角形,,,为上的动点,交折线于点,设,的面积为,则与的函数图象正确的是( )
A. B.
C. D.
3.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PO,设运动时间为xs,△APQ的面积为ycm2,则下列图像中能大致表示y与x的函数关系的是( )
A. B.
C. D.
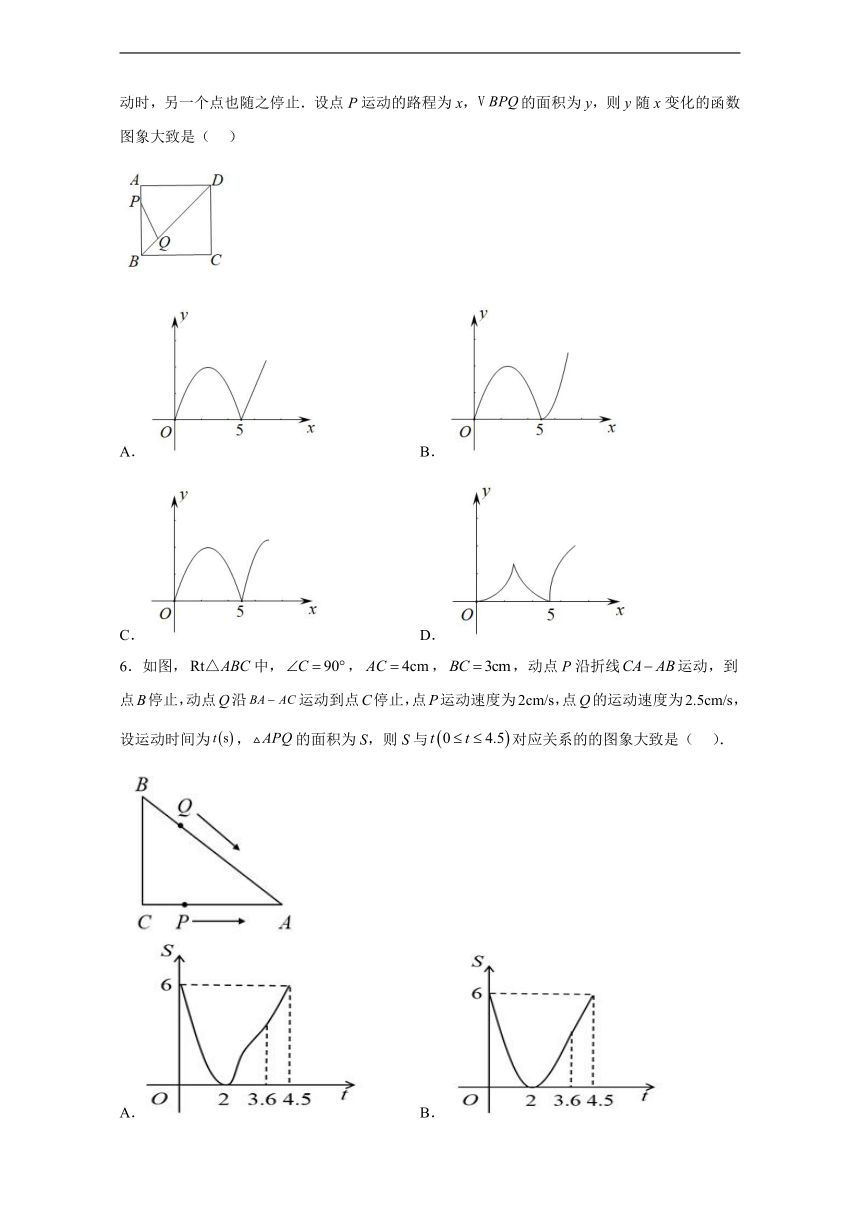
4.如图,四边形ABCD是正方形,AB=2,点P为射线BC上一点,连接DP,将DP绕点P顺时针旋转90°得到线段EP,过B作EP平行线交DC延长线于F.设BP长为x,四边形BFEP的面积为y,下列图象能正确反映出y与x函数关系的是( )
A. B.
C. D.
5.如图,正方形ABCD的边长为5,动点P的运动路线为,动点Q的运动路线为.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点且停止运动时,另一个点也随之停止.设点P运动的路程为x,的面积为y,则y随x变化的函数图象大致是( )
A. B.
C. D.
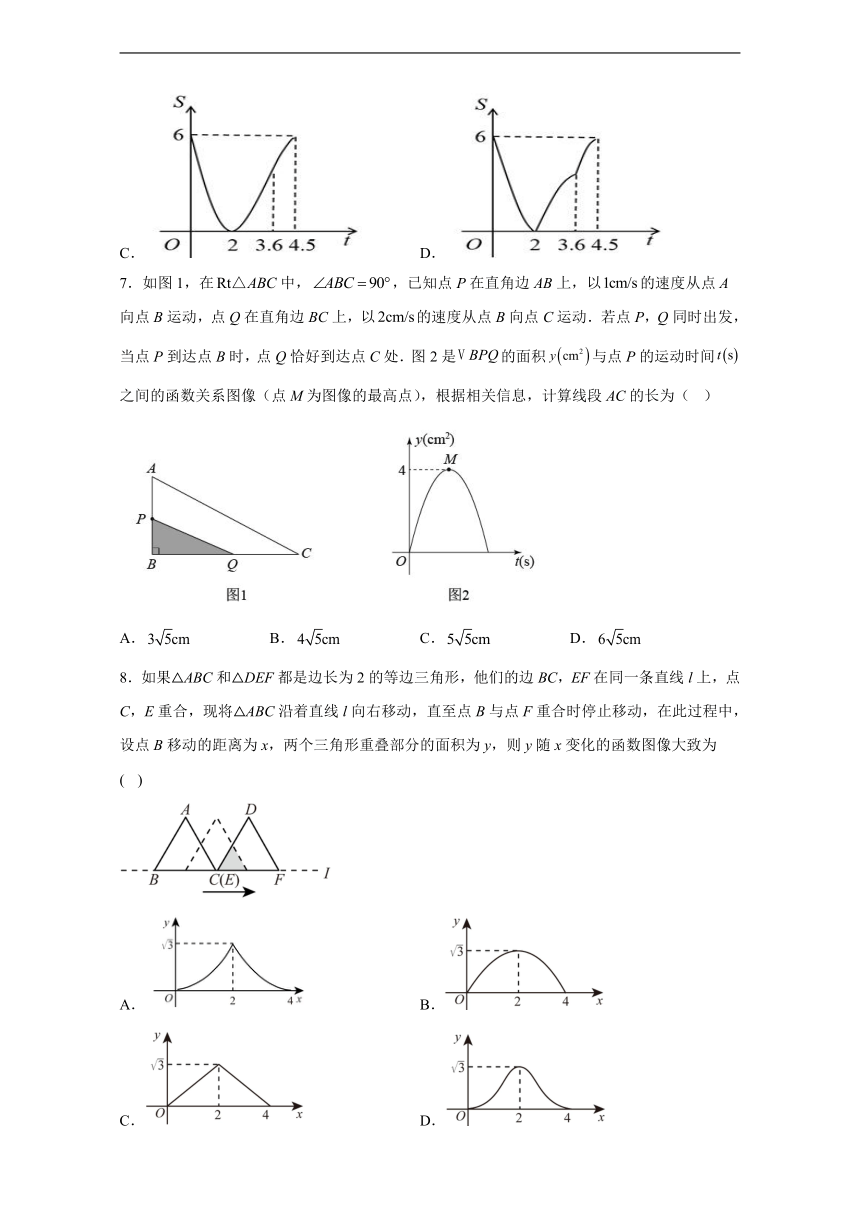
6.如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的的图象大致是( ).
A. B.
C. D.
7.如图1,在中,,已知点P在直角边AB上,以的速度从点A向点B运动,点Q在直角边BC上,以的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处.图2是的面积与点P的运动时间之间的函数关系图像(点M为图像的最高点),根据相关信息,计算线段AC的长为( )
A. B. C. D.
8.如果△ABC和△DEF都是边长为2的等边三角形,他们的边BC,EF在同一条直线l上,点C,E重合,现将△ABC沿着直线l向右移动,直至点B与点F重合时停止移动,在此过程中,设点B移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图像大致为( )
A. B.
C. D.
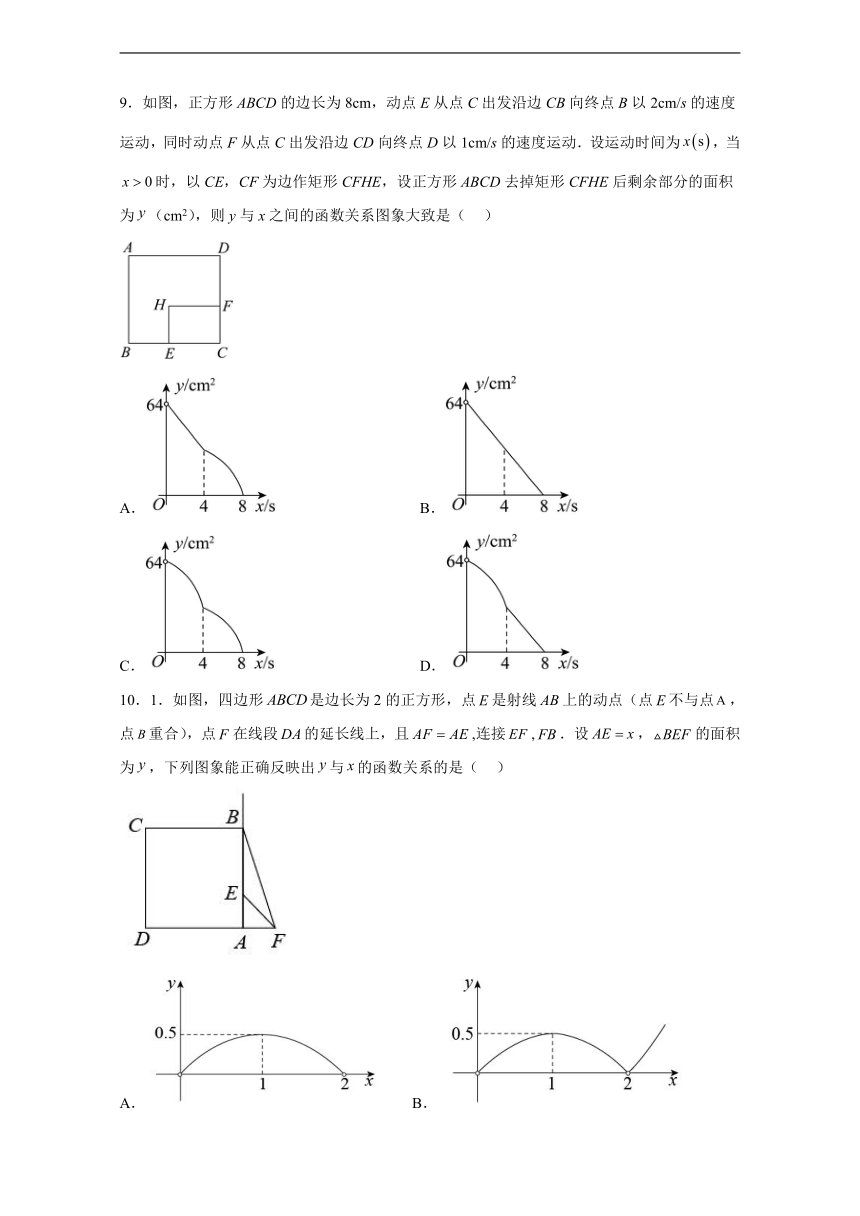
9.如图,正方形ABCD的边长为8cm,动点E从点C出发沿边CB向终点B以2cm/s的速度运动,同时动点F从点C出发沿边CD向终点D以1cm/s的速度运动.设运动时间为,当时,以CE,CF为边作矩形CFHE,设正方形ABCD去掉矩形CFHE后剩余部分的面积为(cm2),则y与x之间的函数关系图象大致是( )
A. B.
C. D.
10.1.如图,四边形是边长为2的正方形,点是射线上的动点(点不与点,点重合),点在线段的延长线上,且,连接,.设,的面积为,下列图象能正确反映出与的函数关系的是( )
A. B.
C. D.
11.如图1,在矩形ABCD中,点E,F,G分别是边AD,BC,AB的中点,连结EF,,点H是EF上一动点,设FH的长为x,GH与BH长度的和为y.图2是y关于x的函数图象,点P为图象上的最低点,则函数图象的右端点Q的坐标为( )
A. B. C. D.
12.如图,四边形是菱形,边长为4,,垂直于的直线从点A出发,沿AD方向以每秒1个单位长度的速度向右平移,设直线EF与菱形的两边分别交于点E,F(点E在点F的上方),若的面积为y,直线的运动时间为x秒(),则能大致反映y与x的函数关系的图象是( )
A. B.
C. D.
二、填空题
13.在平面直角坐标系中,A点坐标为(﹣1,4),B点坐标为(5,4).已知抛物线y=x2﹣2x+c与线段AB有公共点,则c的取值范围是__.
14.如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
15.如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点,连接CD,将△BCD绕点C顺时针旋转90°得到△ACE,连接DE,则△ADE面积的最大值等于____________.
16.如图,在矩形中,,点E是的中点,连接,点M是上一动点,取的中点为N,连接,则的最小值是________.
17.如图,在中,,,为边上的高,动点在上,从点出发,沿方向运动,设,的面积为,矩形的面积为,,则与的关系式是________.
三、解答题
18.如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式:
(2)求CED的面积S与D点运动时间t的函数解析式;当t为何值时,CED的面积最大?最大面积是多少?
19.已知直线交x轴于点A,交y轴于点B,二次函数的图像经过A、B两点.
(1)求二次函数的表达式.
(2)设动点M的横坐标为m,当动点M在AB下方的抛物线上运动时,求△MAB的面积S关于m的函数表达式.
(3)有一条动直线,直线在AO之间移动(包括A,O两端点),直线交抛物线于点Q,当△QAB的面积是△QAO面积的2倍时,求a的值.
20.如图,,,,.,两点分别从,同时出发,点沿折线向终点运动,在上的速度为每秒4个单位长度,在上的速度为每秒2个单位长度;点以每秒个单位长度的速度沿线段向终点A运动.过点作于点,以,为邻边作矩形.设运动时间为秒,矩形和重叠部分的图形面积为.
(1)当点和点重合时,______;
(2)求关于的函数解析式,并写出的取值范围;
(3)在运动过程中,连接,取中点,连接,直接写出的最小值.
21.如图,在正方形ABCD中,,动点P分别从点B点出发,以向点A运动,动点Q从点D出发,以沿着AD延长线运动,当点P运动到A点时,P,Q两点同时停止运动,设动点运动时间为,以AP,AQ为边的矩形APHQ的面积为.
(1)写出S与关于t的函数表达式;
(2)当t时多少时,矩形APHQ的面积最大?最大面积是多少?
参考答案:
1.C
解:∵在直角三角形ABC中,∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵EF⊥BC,ED⊥AC,
∴四边形EFCD是矩形,
∵E是AB的中点,
∴EF=AC,DE=BC,
∴EF=ED,
∴四边形EFCD是正方形,
设正方形的边长为a,如图1,当移动的距离当移动的距离>a 时,如图2,,
∴S关于t的函数图象大致为C选项,故选:C.
2.B
解:由题意可得,
当时,,
当时,,
当时,函数图象为的右半部分,当时,函数图象为的右半部分,
故选:B.
3.A
解:①当0≤x≤2时,
∵正方形的边长为2cm,
∴y=S△APQ=AQ AP=x2;
②当2<x≤4时,
y=S△APQ
=,
=2×2﹣(4﹣x)2﹣×2×(x﹣2)﹣×2×(x﹣2)
=﹣x2+2x,
y与x之间的函数关系可以用两段二次函数图像表示,根据各选项,只有A选项图像符合.
故选:A.
4.D
解:方法一:由题意知,当P点在C点右侧时,BP越大,则则四边形BFEP的面积越大,
故D选项符合题意;
方法二:如下图,当P点在BC之间时,作EH⊥BC于H,
∵∠DPE=90°,
∴∠DPC+∠EPH=90°,
∵∠DPC+∠PDC=90°,
∴∠EPH=∠PDC,
在△EPH和△PDC中,
,
∴△EPH≌△PDC(AAS),
∵BP=x,AB=BC=2,
∴PC=EH=2﹣x,
∴四边形BPEF的面积y=x(2﹣x)=﹣x2+2x,
同理可得当P点在C点右侧时,EH=PC=x﹣2,
∴四边形BPEF的面积y=x(x﹣2)=x2﹣2x,
综上所述,当0<x<2时,函数图象为开口方向向下的抛物线,当x>2时,函数图象为开口方向向上的抛物线,
故选:D.
5.B
解:(1)点P在AB上运动时,0<x≤5,如图,
∵正方形ABCD的边长为5,点P与Q以相同的均匀速度分别从A,B两点同时出发,
作QE⊥AB交AB于点E,
则有AP=BQ=x,∠EBQ=∠DBC=45°,
∴BP=5 x,QE=,
∴△BPQ的面积为:y=BP QE=×(5 x)×=(0<x≤5),
∴此时图象为抛物线开口方向向下;
(2)点P在BC上运动时,5<x≤5,如图,
∵正方形ABCD的边长为5,点P与Q以相同的均匀速度分别从A,B两点同时出发,
作QE⊥BC交BC于点E,
则有AB+BP=BQ=x,∠DBC=45°,
∴BP=x 5,QE=,
∴△BPQ的面积为:y=BP QE=×(x 5)×=(5<x≤5),
∴此时图象是抛物线一部分,开口方向向上,且y随x的增大而增大;
综上,只有选项B的图象符合,
故选:B.
6.B
解:由题意得:AB,
当时,点P在AC上,点Q在AB上,
则AP=AC-CP=4-2t,AQ=AB-BQ=5-2.5t,
如图,过点Q作QM⊥AC于M,
∴sin∠A=,即,
∴,
此时,
当时,点P在AB上,点Q在AC上,
则AP=2t-4,AQ=2.5t-5,
如图,过点P作PN⊥AC于N,
同理可得:,
此时,
∵二次函数的图象开口向上,对称轴为,
∴当时,函数图象为二次函数的图象的一部分,
当时,点Q与点C重合,点P在AB上,
此时,
∴当时,函数图象为直线的一部分,
故选:B.
7.B
解:设运动时间,,则,,
在中,,,,则,
当时,有最大值为,
解得,即,
根据的面积与点P的运动时间之间的函数关系可知,
抛物线与轴交于和两点,即运动时间是,
,
在中,,,
根据勾股定理可得,
故选:B.
8.A
解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GE=EJ=GJ=x,∠GEJ=60°,
∴GH=CGsin60°=EJ=x,
∴y=EJ GH=x2,
当x=2时,y=,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
y=FJ GH=(4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
9.D
解:由题意,CE=2xcm,CF=xcm
∴DF=(8-x)cm.
当0≤x≤2时,
∴
当2<x≤4时,
则
;
所以符合题意的图象为D,
故选D
10.B
解:当点在之间时,即,
,则,
,
图象是开口向下,对称为:的抛物线,
当点在上方时,即,
,则,
,
图象是开口向上的抛物线,
故选:B.
11.D
解:连接CG交EF于H′,当H运动到H′时y最小,由函数图象知, x=1,即FH=1时y最小,
∵在矩形ABCD中,点E,F,G分别是边AD,BC,AB的中点,
∴EF∥AB,EF=AB,BF=AE= BC=3,AG=BG,
∴CH′=GH′,
∴BG=2FH′=2,则AB=4,
当H运动到E点时,y最大,此时FH=EF=4,即x=4,
连接BE、GE,
由勾股定理得:BE= ,GE= ,
∴GH+BH=BE+GE=5+ ,即y=5+ ,
∴Q点坐标为(4,5+ ),
故选:D.
12.C
解:如图1,过点B作BH⊥AB点H,
∵四边形ABCD是菱形四边形,边长为4,
∴AB=AD=4,
∵ ∠A=60°,
∴∠ABH=90°-∠A=30°,
∴AH=AB=2,
由勾股定理得
.
∴.
∵ EF⊥AB于点F,
∴∠AFE=90°,
在Rt△AEF中,∠AEF=90°-∠A=30°,AF=x,
∴AE=2AF=2x,
由勾股定理得,
∴,
∴ ,
∴当时,
的面积为y=AF×EF=.
∵ ,抛物线y=对称轴为y轴,
∴抛物线y=开口向上,
当,y随着x的增大而增大.
∴ 当时,此时点EF运动到BH的位置,
y有最大值,最大值是y=;
当时,如图2,作DG⊥BC于点G,
∵ BCAD,
∴DG=EF=BH=.
的面积为y=AF×EF==.
∵=>0,
∴当时,y随着x的增大而增大,
∴ 当时,此时EF运动到GD的位置,
y有最大值,最大值是y=4,
综上所述,y与x的函数关系式为.
根据y与x的函数关系可判断应该选C,
故选:C.
13.
解:∵y=x2﹣2x+c=(x﹣1)2+c﹣1,
∴抛物线开口向上,顶点坐标为(1,c﹣1),对称轴为直线x=1,
如图,当c﹣1=4时,c=5,抛物线顶点落在线段AB上,抛物线与线段AB刚好有一个交点,满足题意,
c减小,图象向下移动,当抛物线经过点B时,抛物线和线段又只有一个交点,如图,
把(5,4)代入y=x2﹣2x+c得:
4=25﹣10+c,
解得c=﹣11,
∴﹣11≤c≤5满足题意.
故答案为:﹣11≤c≤5.
14.8
解:当点C横坐标为 3时,抛物线顶点为A(1,4),对称轴为x=1,
此时D点横坐标为5,则CD=8,
当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,
故C(0,0),D(8,0),
此时D点横坐标最大,故点D的横坐标最大值为8.
故答案为:8.
15.
解:如图,△BCD绕点C顺时针旋转90°得到△ACE,
∴△BDC≌△AEC,
∴∠B=∠CAE,
∵BC=AC=,△ABC为等腰直角三角形,
∴∠B=∠CAE=∠BAC=45°,
∴∠DAE=∠BAC+∠CAE=90°,
在Rt△ABC中,由勾股定理AB=,
设BD=AE=x,则AD=(2-x),
∴,
∵,函数开口向下,函数有最大值,
当x=1时,.
故答案为:.
16.
解:以点为原点,建立平面直角坐标系,如下图所示:
在矩形中,,点是的中点,
,
∴,
直线的函数解析式为,
设点的坐标为,
点是上一动点,
,
点是的中点,
,
由两点之间的距离公式得:,
由二次函数的性质得:在内,随的增大而增大,
则当时,取得最小值,最小值为36,
因此,的最小值为,
故答案为:.
17.
解:在中,,,
∴,
∵为边上的高,
∴AD=BD=DC=
设,
∴PD=,
∵矩形,由于DF在BC上,
∴PE∥DC,
∴∠AEP=∠C=∠DAC=45 ,
∴PE=AP=x,
S1=,
S2=,
∴,
.
故答案为:.
18.(1)y=-x2+3x+8
(2)S=-t2+5t,当t=5时,CED的面积最大,最大面积是
(1)
解:将点A(0,8)、B(8,0)代入抛物线y=-x2+bx+c得:
,
解得:,
故抛物线的解析式为:y=-x2+3x+8,
(2)
解:根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8-t,
∴DE=OE+OD=10-t,
∴S= DE OC= (10-t) t=-t2+5t,
即S=-t2+5t=-(t-5)2+,
∴当t=5时,S最大=.
∴CED的面积S与D点运动时间t的函数解析式S=-t2+5t,当t=5时,CED的面积最大,最大面积是.
19.(1)
(2)
(3)或
(1)
解:∵直线交x轴于点A,交y轴于点B,
∴点A为(-3,0),点B为(0,6).将A,B点代入中,得
,解得
故抛物线表达式为.
(2)
如图,过点M作轴交AB于点P,
故P点坐标为(m,),M点坐标为(m,),
∴.
∵△MAB的面积=△MPA的面积+△MPB的面积,
∴.
(3)
根据题意可知Q点横坐标为,
由(2)可知,
∵△QAB的面积是△QAO面积的2倍,
∴
解得(舍)或或.
20.(1)
(2)当时,;当时,;当时,
(3)
(1)
解:在中,,,,
,
在上的速度为每秒4个单位长度,点以每秒个单位长度的速度沿线段向终点A运动,设运动时间为秒,则,
在中,,,,则,
当点和点重合时,,即,解得,
故答案为:;
(2)
解:如图①,当时,
在中,,,
∴,,
∴,
∴;
如图②,当时,
在中,,,
∴,
∵,
∴,
如图③,当时,
在中,,,
∴,
∴
;
(3)
解:如图①,当时,
由(1)(2)知,,,
取中点,连接,
,,
,
开口向上,对称轴为,
当时,有最小值,为;
如图②,当时,
由(1)(2)知,,,
取中点,连接,
,,
,
开口向上,对称轴为,,
当时,有最小值,为;
如图③,当时,
由(1)(2)知,,
取中点,连接,
,
开口向上,对称轴为,,
当时,有最小值,为;
,
最小值为.
21.(1)
(2)当t=2时,矩形APHQ的面积最大,最大面积是72cm2
(1)
解:由题意得cm,cm,
cm,cm,
;
(2)
解:,
∴当t=2时,矩形APHQ的面积最大,最大面积是72cm2.
一、单选题
1.如图,在Rt△ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,则S关于t的函数图象大致为( )
A. B.
C. D.
2.如图,是等腰直角三角形,,,为上的动点,交折线于点,设,的面积为,则与的函数图象正确的是( )
A. B.
C. D.
3.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PO,设运动时间为xs,△APQ的面积为ycm2,则下列图像中能大致表示y与x的函数关系的是( )
A. B.
C. D.
4.如图,四边形ABCD是正方形,AB=2,点P为射线BC上一点,连接DP,将DP绕点P顺时针旋转90°得到线段EP,过B作EP平行线交DC延长线于F.设BP长为x,四边形BFEP的面积为y,下列图象能正确反映出y与x函数关系的是( )
A. B.
C. D.
5.如图,正方形ABCD的边长为5,动点P的运动路线为,动点Q的运动路线为.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点且停止运动时,另一个点也随之停止.设点P运动的路程为x,的面积为y,则y随x变化的函数图象大致是( )
A. B.
C. D.
6.如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的的图象大致是( ).
A. B.
C. D.
7.如图1,在中,,已知点P在直角边AB上,以的速度从点A向点B运动,点Q在直角边BC上,以的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处.图2是的面积与点P的运动时间之间的函数关系图像(点M为图像的最高点),根据相关信息,计算线段AC的长为( )
A. B. C. D.
8.如果△ABC和△DEF都是边长为2的等边三角形,他们的边BC,EF在同一条直线l上,点C,E重合,现将△ABC沿着直线l向右移动,直至点B与点F重合时停止移动,在此过程中,设点B移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图像大致为( )
A. B.
C. D.
9.如图,正方形ABCD的边长为8cm,动点E从点C出发沿边CB向终点B以2cm/s的速度运动,同时动点F从点C出发沿边CD向终点D以1cm/s的速度运动.设运动时间为,当时,以CE,CF为边作矩形CFHE,设正方形ABCD去掉矩形CFHE后剩余部分的面积为(cm2),则y与x之间的函数关系图象大致是( )
A. B.
C. D.
10.1.如图,四边形是边长为2的正方形,点是射线上的动点(点不与点,点重合),点在线段的延长线上,且,连接,.设,的面积为,下列图象能正确反映出与的函数关系的是( )
A. B.
C. D.
11.如图1,在矩形ABCD中,点E,F,G分别是边AD,BC,AB的中点,连结EF,,点H是EF上一动点,设FH的长为x,GH与BH长度的和为y.图2是y关于x的函数图象,点P为图象上的最低点,则函数图象的右端点Q的坐标为( )
A. B. C. D.
12.如图,四边形是菱形,边长为4,,垂直于的直线从点A出发,沿AD方向以每秒1个单位长度的速度向右平移,设直线EF与菱形的两边分别交于点E,F(点E在点F的上方),若的面积为y,直线的运动时间为x秒(),则能大致反映y与x的函数关系的图象是( )
A. B.
C. D.
二、填空题
13.在平面直角坐标系中,A点坐标为(﹣1,4),B点坐标为(5,4).已知抛物线y=x2﹣2x+c与线段AB有公共点,则c的取值范围是__.
14.如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
15.如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点,连接CD,将△BCD绕点C顺时针旋转90°得到△ACE,连接DE,则△ADE面积的最大值等于____________.
16.如图,在矩形中,,点E是的中点,连接,点M是上一动点,取的中点为N,连接,则的最小值是________.
17.如图,在中,,,为边上的高,动点在上,从点出发,沿方向运动,设,的面积为,矩形的面积为,,则与的关系式是________.
三、解答题
18.如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式:
(2)求CED的面积S与D点运动时间t的函数解析式;当t为何值时,CED的面积最大?最大面积是多少?
19.已知直线交x轴于点A,交y轴于点B,二次函数的图像经过A、B两点.
(1)求二次函数的表达式.
(2)设动点M的横坐标为m,当动点M在AB下方的抛物线上运动时,求△MAB的面积S关于m的函数表达式.
(3)有一条动直线,直线在AO之间移动(包括A,O两端点),直线交抛物线于点Q,当△QAB的面积是△QAO面积的2倍时,求a的值.
20.如图,,,,.,两点分别从,同时出发,点沿折线向终点运动,在上的速度为每秒4个单位长度,在上的速度为每秒2个单位长度;点以每秒个单位长度的速度沿线段向终点A运动.过点作于点,以,为邻边作矩形.设运动时间为秒,矩形和重叠部分的图形面积为.
(1)当点和点重合时,______;
(2)求关于的函数解析式,并写出的取值范围;
(3)在运动过程中,连接,取中点,连接,直接写出的最小值.
21.如图,在正方形ABCD中,,动点P分别从点B点出发,以向点A运动,动点Q从点D出发,以沿着AD延长线运动,当点P运动到A点时,P,Q两点同时停止运动,设动点运动时间为,以AP,AQ为边的矩形APHQ的面积为.
(1)写出S与关于t的函数表达式;
(2)当t时多少时,矩形APHQ的面积最大?最大面积是多少?
参考答案:
1.C
解:∵在直角三角形ABC中,∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵EF⊥BC,ED⊥AC,
∴四边形EFCD是矩形,
∵E是AB的中点,
∴EF=AC,DE=BC,
∴EF=ED,
∴四边形EFCD是正方形,
设正方形的边长为a,如图1,当移动的距离
∴S关于t的函数图象大致为C选项,故选:C.
2.B
解:由题意可得,
当时,,
当时,,
当时,函数图象为的右半部分,当时,函数图象为的右半部分,
故选:B.
3.A
解:①当0≤x≤2时,
∵正方形的边长为2cm,
∴y=S△APQ=AQ AP=x2;
②当2<x≤4时,
y=S△APQ
=,
=2×2﹣(4﹣x)2﹣×2×(x﹣2)﹣×2×(x﹣2)
=﹣x2+2x,
y与x之间的函数关系可以用两段二次函数图像表示,根据各选项,只有A选项图像符合.
故选:A.
4.D
解:方法一:由题意知,当P点在C点右侧时,BP越大,则则四边形BFEP的面积越大,
故D选项符合题意;
方法二:如下图,当P点在BC之间时,作EH⊥BC于H,
∵∠DPE=90°,
∴∠DPC+∠EPH=90°,
∵∠DPC+∠PDC=90°,
∴∠EPH=∠PDC,
在△EPH和△PDC中,
,
∴△EPH≌△PDC(AAS),
∵BP=x,AB=BC=2,
∴PC=EH=2﹣x,
∴四边形BPEF的面积y=x(2﹣x)=﹣x2+2x,
同理可得当P点在C点右侧时,EH=PC=x﹣2,
∴四边形BPEF的面积y=x(x﹣2)=x2﹣2x,
综上所述,当0<x<2时,函数图象为开口方向向下的抛物线,当x>2时,函数图象为开口方向向上的抛物线,
故选:D.
5.B
解:(1)点P在AB上运动时,0<x≤5,如图,
∵正方形ABCD的边长为5,点P与Q以相同的均匀速度分别从A,B两点同时出发,
作QE⊥AB交AB于点E,
则有AP=BQ=x,∠EBQ=∠DBC=45°,
∴BP=5 x,QE=,
∴△BPQ的面积为:y=BP QE=×(5 x)×=(0<x≤5),
∴此时图象为抛物线开口方向向下;
(2)点P在BC上运动时,5<x≤5,如图,
∵正方形ABCD的边长为5,点P与Q以相同的均匀速度分别从A,B两点同时出发,
作QE⊥BC交BC于点E,
则有AB+BP=BQ=x,∠DBC=45°,
∴BP=x 5,QE=,
∴△BPQ的面积为:y=BP QE=×(x 5)×=(5<x≤5),
∴此时图象是抛物线一部分,开口方向向上,且y随x的增大而增大;
综上,只有选项B的图象符合,
故选:B.
6.B
解:由题意得:AB,
当时,点P在AC上,点Q在AB上,
则AP=AC-CP=4-2t,AQ=AB-BQ=5-2.5t,
如图,过点Q作QM⊥AC于M,
∴sin∠A=,即,
∴,
此时,
当时,点P在AB上,点Q在AC上,
则AP=2t-4,AQ=2.5t-5,
如图,过点P作PN⊥AC于N,
同理可得:,
此时,
∵二次函数的图象开口向上,对称轴为,
∴当时,函数图象为二次函数的图象的一部分,
当时,点Q与点C重合,点P在AB上,
此时,
∴当时,函数图象为直线的一部分,
故选:B.
7.B
解:设运动时间,,则,,
在中,,,,则,
当时,有最大值为,
解得,即,
根据的面积与点P的运动时间之间的函数关系可知,
抛物线与轴交于和两点,即运动时间是,
,
在中,,,
根据勾股定理可得,
故选:B.
8.A
解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GE=EJ=GJ=x,∠GEJ=60°,
∴GH=CGsin60°=EJ=x,
∴y=EJ GH=x2,
当x=2时,y=,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
y=FJ GH=(4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
9.D
解:由题意,CE=2xcm,CF=xcm
∴DF=(8-x)cm.
当0≤x≤2时,
∴
当2<x≤4时,
则
;
所以符合题意的图象为D,
故选D
10.B
解:当点在之间时,即,
,则,
,
图象是开口向下,对称为:的抛物线,
当点在上方时,即,
,则,
,
图象是开口向上的抛物线,
故选:B.
11.D
解:连接CG交EF于H′,当H运动到H′时y最小,由函数图象知, x=1,即FH=1时y最小,
∵在矩形ABCD中,点E,F,G分别是边AD,BC,AB的中点,
∴EF∥AB,EF=AB,BF=AE= BC=3,AG=BG,
∴CH′=GH′,
∴BG=2FH′=2,则AB=4,
当H运动到E点时,y最大,此时FH=EF=4,即x=4,
连接BE、GE,
由勾股定理得:BE= ,GE= ,
∴GH+BH=BE+GE=5+ ,即y=5+ ,
∴Q点坐标为(4,5+ ),
故选:D.
12.C
解:如图1,过点B作BH⊥AB点H,
∵四边形ABCD是菱形四边形,边长为4,
∴AB=AD=4,
∵ ∠A=60°,
∴∠ABH=90°-∠A=30°,
∴AH=AB=2,
由勾股定理得
.
∴.
∵ EF⊥AB于点F,
∴∠AFE=90°,
在Rt△AEF中,∠AEF=90°-∠A=30°,AF=x,
∴AE=2AF=2x,
由勾股定理得,
∴,
∴ ,
∴当时,
的面积为y=AF×EF=.
∵ ,抛物线y=对称轴为y轴,
∴抛物线y=开口向上,
当,y随着x的增大而增大.
∴ 当时,此时点EF运动到BH的位置,
y有最大值,最大值是y=;
当时,如图2,作DG⊥BC于点G,
∵ BCAD,
∴DG=EF=BH=.
的面积为y=AF×EF==.
∵=>0,
∴当时,y随着x的增大而增大,
∴ 当时,此时EF运动到GD的位置,
y有最大值,最大值是y=4,
综上所述,y与x的函数关系式为.
根据y与x的函数关系可判断应该选C,
故选:C.
13.
解:∵y=x2﹣2x+c=(x﹣1)2+c﹣1,
∴抛物线开口向上,顶点坐标为(1,c﹣1),对称轴为直线x=1,
如图,当c﹣1=4时,c=5,抛物线顶点落在线段AB上,抛物线与线段AB刚好有一个交点,满足题意,
c减小,图象向下移动,当抛物线经过点B时,抛物线和线段又只有一个交点,如图,
把(5,4)代入y=x2﹣2x+c得:
4=25﹣10+c,
解得c=﹣11,
∴﹣11≤c≤5满足题意.
故答案为:﹣11≤c≤5.
14.8
解:当点C横坐标为 3时,抛物线顶点为A(1,4),对称轴为x=1,
此时D点横坐标为5,则CD=8,
当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,
故C(0,0),D(8,0),
此时D点横坐标最大,故点D的横坐标最大值为8.
故答案为:8.
15.
解:如图,△BCD绕点C顺时针旋转90°得到△ACE,
∴△BDC≌△AEC,
∴∠B=∠CAE,
∵BC=AC=,△ABC为等腰直角三角形,
∴∠B=∠CAE=∠BAC=45°,
∴∠DAE=∠BAC+∠CAE=90°,
在Rt△ABC中,由勾股定理AB=,
设BD=AE=x,则AD=(2-x),
∴,
∵,函数开口向下,函数有最大值,
当x=1时,.
故答案为:.
16.
解:以点为原点,建立平面直角坐标系,如下图所示:
在矩形中,,点是的中点,
,
∴,
直线的函数解析式为,
设点的坐标为,
点是上一动点,
,
点是的中点,
,
由两点之间的距离公式得:,
由二次函数的性质得:在内,随的增大而增大,
则当时,取得最小值,最小值为36,
因此,的最小值为,
故答案为:.
17.
解:在中,,,
∴,
∵为边上的高,
∴AD=BD=DC=
设,
∴PD=,
∵矩形,由于DF在BC上,
∴PE∥DC,
∴∠AEP=∠C=∠DAC=45 ,
∴PE=AP=x,
S1=,
S2=,
∴,
.
故答案为:.
18.(1)y=-x2+3x+8
(2)S=-t2+5t,当t=5时,CED的面积最大,最大面积是
(1)
解:将点A(0,8)、B(8,0)代入抛物线y=-x2+bx+c得:
,
解得:,
故抛物线的解析式为:y=-x2+3x+8,
(2)
解:根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8-t,
∴DE=OE+OD=10-t,
∴S= DE OC= (10-t) t=-t2+5t,
即S=-t2+5t=-(t-5)2+,
∴当t=5时,S最大=.
∴CED的面积S与D点运动时间t的函数解析式S=-t2+5t,当t=5时,CED的面积最大,最大面积是.
19.(1)
(2)
(3)或
(1)
解:∵直线交x轴于点A,交y轴于点B,
∴点A为(-3,0),点B为(0,6).将A,B点代入中,得
,解得
故抛物线表达式为.
(2)
如图,过点M作轴交AB于点P,
故P点坐标为(m,),M点坐标为(m,),
∴.
∵△MAB的面积=△MPA的面积+△MPB的面积,
∴.
(3)
根据题意可知Q点横坐标为,
由(2)可知,
∵△QAB的面积是△QAO面积的2倍,
∴
解得(舍)或或.
20.(1)
(2)当时,;当时,;当时,
(3)
(1)
解:在中,,,,
,
在上的速度为每秒4个单位长度,点以每秒个单位长度的速度沿线段向终点A运动,设运动时间为秒,则,
在中,,,,则,
当点和点重合时,,即,解得,
故答案为:;
(2)
解:如图①,当时,
在中,,,
∴,,
∴,
∴;
如图②,当时,
在中,,,
∴,
∵,
∴,
如图③,当时,
在中,,,
∴,
∴
;
(3)
解:如图①,当时,
由(1)(2)知,,,
取中点,连接,
,,
,
开口向上,对称轴为,
当时,有最小值,为;
如图②,当时,
由(1)(2)知,,,
取中点,连接,
,,
,
开口向上,对称轴为,,
当时,有最小值,为;
如图③,当时,
由(1)(2)知,,
取中点,连接,
,
开口向上,对称轴为,,
当时,有最小值,为;
,
最小值为.
21.(1)
(2)当t=2时,矩形APHQ的面积最大,最大面积是72cm2
(1)
解:由题意得cm,cm,
cm,cm,
;
(2)
解:,
∴当t=2时,矩形APHQ的面积最大,最大面积是72cm2.
同课章节目录
