2022--2023学年人教版九年级数学上册第24章 圆 分层练习(含答案)
文档属性
| 名称 | 2022--2023学年人教版九年级数学上册第24章 圆 分层练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:25:35 | ||
图片预览



文档简介
第24章 圆 分层练习
A基础篇(10min)
1.下列说法,其中正确的有( )
①过圆心的线段是直径
②圆上的一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形
③大于半圆的弧叫做劣弧
④圆心相同,半径不等的圆叫做同心圆
A.1个 B.2个 C.3个 D.4个
2.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
3.如图,在⊙O中,点C是的中点,若∠ABC=65°,则∠D的度数是( )
A.75° B.65° C.50° D.40°
4.如图,点A,B,C在⊙O上,为优弧,已知50°,则∠C为( )
A.25° B.35° C.40° D.50°
5.如图,AB是 O的直径,3,则∠BAC=( )
A.67.5° B.45° C.30° D.22.5°
6.如图,⊙O的内接四边形ABCD中,∠D=50°,则∠B为( )
A.140° B.130° C.120° D.100°
7.如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=15°,则∠BDC=( )
A.85° B.75° C.70° D.65°
8.如图,BD是⊙O的直径,A,C在圆上,∠A=50°,∠DBC的度数是( )
A.50° B.45° C.40° D.35°
9.如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为( )
A.138° B.121° C.118° D.112°
10.如图,已知∠ABC=60°,点D为BA边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段OB长为半径作弧,交BC于点E,连接DE,则BE的长是( )
A.5 B.5 C.5 D.5
11.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 .
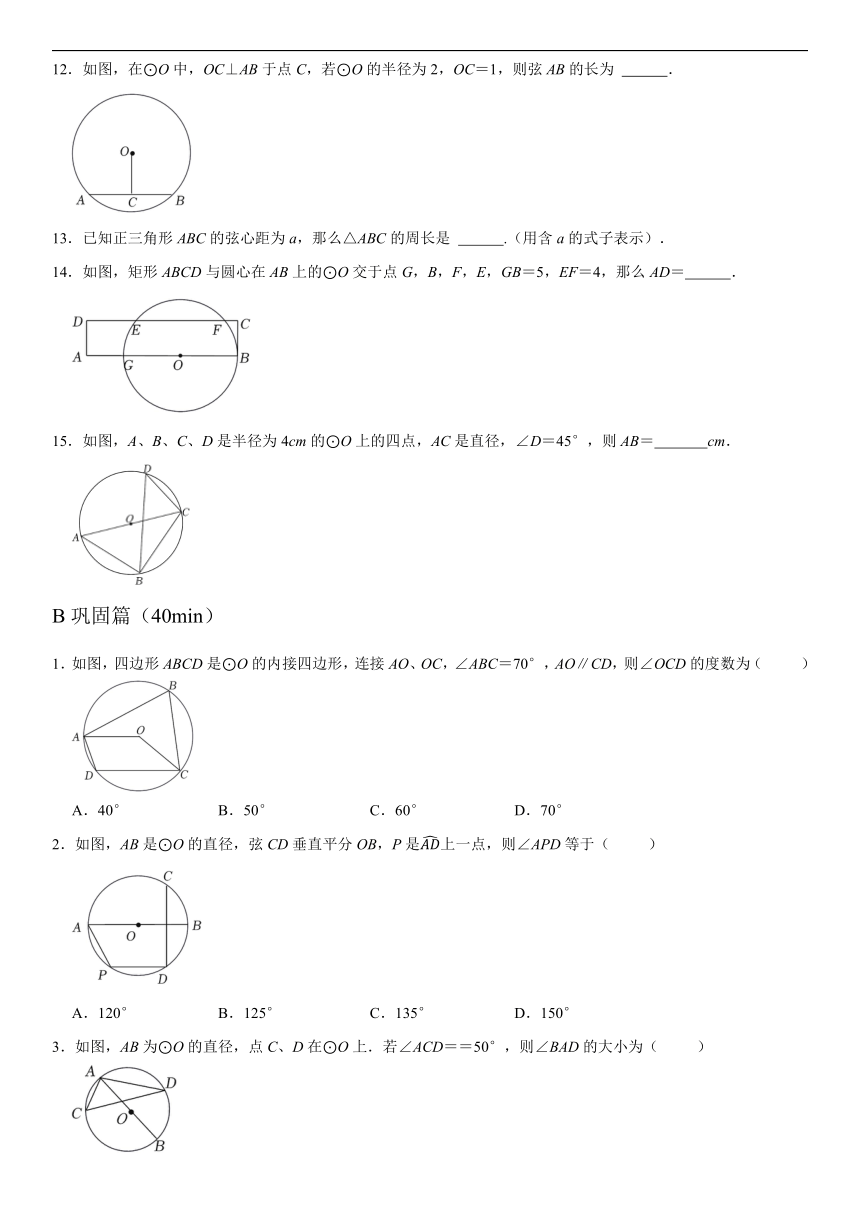
12.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为2,OC=1,则弦AB的长为 .
13.已知正三角形ABC的弦心距为a,那么△ABC的周长是 .(用含a的式子表示).
14.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
15.如图,A、B、C、D是半径为4cm的⊙O上的四点,AC是直径,∠D=45°,则AB= cm.
B巩固篇(40min)
1.如图,四边形ABCD是⊙O的内接四边形,连接AO、OC,∠ABC=70°,AO∥CD,则∠OCD的度数为( )
A.40° B.50° C.60° D.70°
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于( )
A.120° B.125° C.135° D.150°
3.如图,AB为⊙O的直径,点C、D在⊙O上.若∠ACD==50°,则∠BAD的大小为( )
A.25° B.30° C.40° D.50°
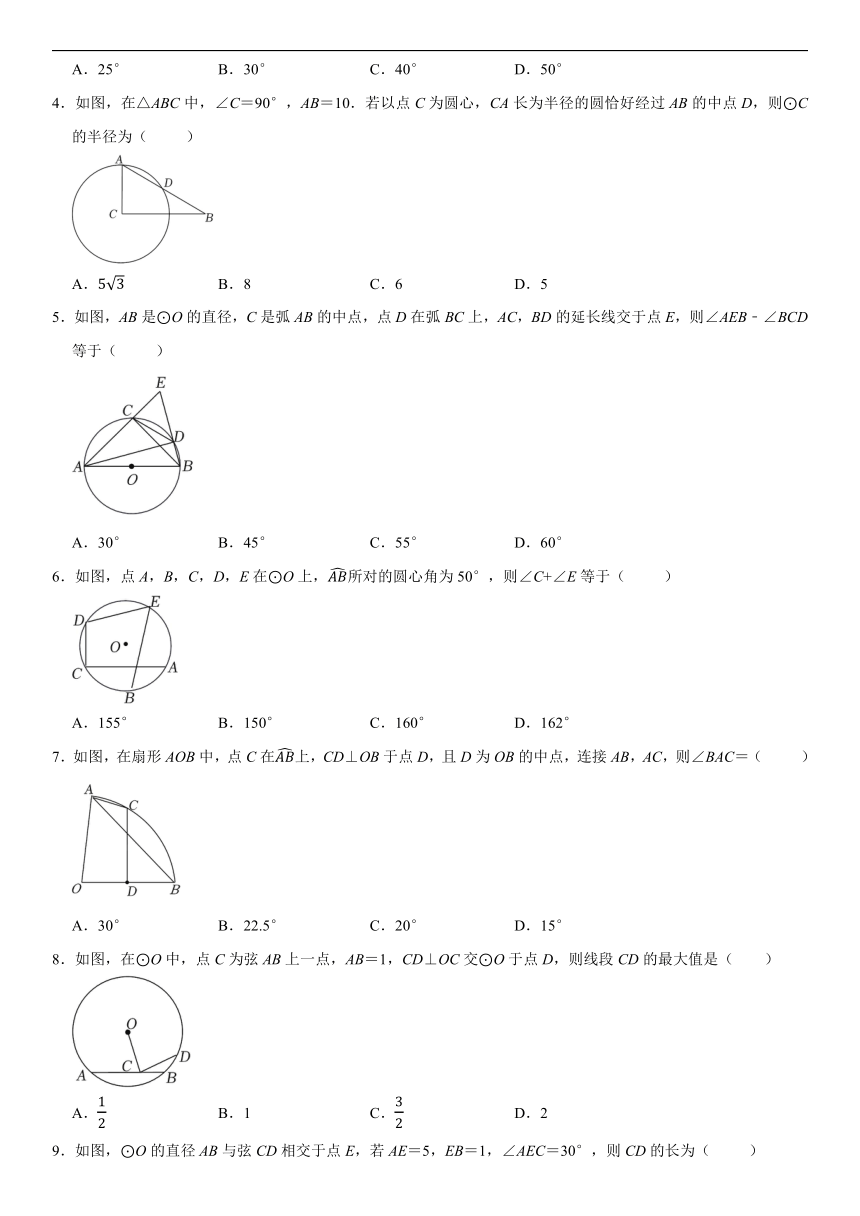
4.如图,在△ABC中,∠C=90°,AB=10.若以点C为圆心,CA长为半径的圆恰好经过AB的中点D,则⊙C的半径为( )
A. B.8 C.6 D.5
5.如图,AB是⊙O的直径,C是弧AB的中点,点D在弧BC上,AC,BD的延长线交于点E,则∠AEB﹣∠BCD等于( )
A.30° B.45° C.55° D.60°
6.如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于( )
A.155° B.150° C.160° D.162°
7.如图,在扇形AOB中,点C在上,CD⊥OB于点D,且D为OB的中点,连接AB,AC,则∠BAC=( )
A.30° B.22.5° C.20° D.15°
8.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( )
A. B.1 C. D.2
9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC=30°,则CD的长为( )
A.5 B.2 C.4 D.
10.如图,在四边形ABCD中,AB=AC=AD=3,∠DBC=15°,∠BDC=30°,则点A到BD的距离是( )
A.3 B. C.2 D.
11.如图,AB是⊙O的直径,且CD⊥AB于E,若AE=1,∠D=30°,则AB= .
12.如图,⊙O的半径为9cm,AB是弦,OC⊥AB于点C,将劣弧AB沿弦AB折叠交于OC的中点D,则AB的长为 .
13.如图,在平面直角坐标系xOy中,直线y与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
14.在半径为13cm的圆内有两条互相平行的弦,一条弦长为24cm,另一条弦长为10cm,则这两条弦之间的距离为 cm.
15.如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,则∠AOC= 度.
16.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=32,则⊙O的半径为 .
17.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
18.如图,AB和OC分别是⊙O的直径和半径,∠BOC=60°,点P是直径AB上的一个动点,射线CP与⊙O相交于点Q,若△POQ是等腰三角形,则∠CPB= .
19.如图,BD是⊙O的直径,,点C是半圆上一动点,且与点A分别在BD的两侧.
(1)如图1,若5,BD=4,求AC的长;
(2)求证:CD+BCAC.
C提升篇
1.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
2.如图,弧AB所对的圆心角为∠AOB=120°,半径OB=2,C是OA的中点,P是弧AB上一动点,以CP为边作等边△CPQ(O,Q两点位于CP同侧),当P从A向B运动过程中,BQ的最小值为 .
3.如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
课后练习
1.如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=( )
A. B. C.1 D.2
2.如图,AB是⊙O的直径,点D是⊙O上一点OC为⊙O的半径,连接AD、CD.若∠D=40°,则∠COB的度数是( )
A.110° B.100° C.140° D.120°
3.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D= °.
4.一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为 厘米.
5.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= .
6.如图,AB是圆O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=8,求圆O的半径.
第24章 圆 分层练习(答案)
A基础篇(10min)
1.下列说法,其中正确的有( B )
①过圆心的线段是直径
②圆上的一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形
③大于半圆的弧叫做劣弧
④圆心相同,半径不等的圆叫做同心圆
A.1个 B.2个 C.3个 D.4个
2.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( B )
A.4cm B.6cm C.8cm D.10cm
3.如图,在⊙O中,点C是的中点,若∠ABC=65°,则∠D的度数是( C )
A.75° B.65° C.50° D.40°
4.如图,点A,B,C在⊙O上,为优弧,已知50°,则∠C为( A )
A.25° B.35° C.40° D.50°
5.如图,AB是 O的直径,3,则∠BAC=( D )
A.67.5° B.45° C.30° D.22.5°
6.如图,⊙O的内接四边形ABCD中,∠D=50°,则∠B为( B )
A.140° B.130° C.120° D.100°
7.如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=15°,则∠BDC=( B )
A.85° B.75° C.70° D.65°
8.如图,BD是⊙O的直径,A,C在圆上,∠A=50°,∠DBC的度数是( C )
A.50° B.45° C.40° D.35°
9.如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为( C )
A.138° B.121° C.118° D.112°
10.如图,已知∠ABC=60°,点D为BA边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段OB长为半径作弧,交BC于点E,连接DE,则BE的长是( A )
A.5 B.5 C.5 D.5
11.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 4 .
12.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为2,OC=1,则弦AB的长为 2 .
13.已知正三角形ABC的弦心距为a,那么△ABC的周长是 6a .(用含a的式子表示).
14.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= 1.5 .
15.如图,A、B、C、D是半径为4cm的⊙O上的四点,AC是直径,∠D=45°,则AB= cm.
B巩固篇(40min)
1.如图,四边形ABCD是⊙O的内接四边形,连接AO、OC,∠ABC=70°,AO∥CD,则∠OCD的度数为( A )
A.40° B.50° C.60° D.70°
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于( A )
A.120° B.125° C.135° D.150°
3.如图,AB为⊙O的直径,点C、D在⊙O上.若∠ACD==50°,则∠BAD的大小为( C )
A.25° B.30° C.40° D.50°
4.如图,在△ABC中,∠C=90°,AB=10.若以点C为圆心,CA长为半径的圆恰好经过AB的中点D,则⊙C的半径为( D )
A. B.8 C.6 D.5
5.如图,AB是⊙O的直径,C是弧AB的中点,点D在弧BC上,AC,BD的延长线交于点E,则∠AEB﹣∠BCD等于( B )
A.30° B.45° C.55° D.60°
6.如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于( A )
A.155° B.150° C.160° D.162°
7.如图,在扇形AOB中,点C在上,CD⊥OB于点D,且D为OB的中点,连接AB,AC,则∠BAC=( A )
A.30° B.22.5° C.20° D.15°
8.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( A )
A. B.1 C. D.2
9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC=30°,则CD的长为( C )
A.5 B.2 C.4 D.
10.如图,在四边形ABCD中,AB=AC=AD=3,∠DBC=15°,∠BDC=30°,则点A到BD的距离是( B )
A.3 B. C.2 D.
11.如图,AB是⊙O的直径,且CD⊥AB于E,若AE=1,∠D=30°,则AB= 4 .
12.如图,⊙O的半径为9cm,AB是弦,OC⊥AB于点C,将劣弧AB沿弦AB折叠交于OC的中点D,则AB的长为 6cm .
13.如图,在平面直角坐标系xOy中,直线y与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 3 .
14.在半径为13cm的圆内有两条互相平行的弦,一条弦长为24cm,另一条弦长为10cm,则这两条弦之间的距离为 17或7 cm.
15.如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,则∠AOC= 125 度.
16.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=32,则⊙O的半径为 4 .
17.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
18.如图,AB和OC分别是⊙O的直径和半径,∠BOC=60°,点P是直径AB上的一个动点,射线CP与⊙O相交于点Q,若△POQ是等腰三角形,则∠CPB= 100°或40°或80° .
19.如图,BD是⊙O的直径,,点C是半圆上一动点,且与点A分别在BD的两侧.
(1)如图1,若5,BD=4,求AC的长;
(2)求证:CD+BCAC.
【解答】(1)解:连接CO并延长交⊙O于点E,连接AE,
∵BD是⊙O的直径,
∴∠BAD=90°,
∵,
∴AB=AD,
∴∠ADB=∠ABD=45°,
∵5,
∴∠BOC∠COD,
∴∠BOC∠BOD=180°30°,
∴∠BDC∠BOC=15°,
∴∠ADC=∠ADB+∠BDC=60°,
∴∠ADC=∠AEC=60°,
∵CE是⊙O的直径,
∴∠CAE=90°,
∵CE=BD=4,
∴AC=CEsin60°=42;
(2)证明:过点A作FA⊥AC,交CD的延长线于点F,
∴∠CAF=90°,
∵∠BAD=90°,
∴∠BAD﹣∠CAD=∠CAF﹣∠CAD,
∴∠BAC=∠DAF,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADF=180°,
∴∠ADF=∠ABC,
∵AB=AD,
∴△ABC≌△ADF(ASA),
∴AC=AF,BC=DF,
∴△ACF是等腰直角三角形,
∴CFAC,
∴CD+DFAC,
∴CD+BCAC.
C提升篇
1.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( C )
A.4 B.5 C.6 D.7
2.如图,弧AB所对的圆心角为∠AOB=120°,半径OB=2,C是OA的中点,P是弧AB上一动点,以CP为边作等边△CPQ(O,Q两点位于CP同侧),当P从A向B运动过程中,BQ的最小值为 1 .
3.如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
课后练习
1.如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=( C )
A. B. C.1 D.2
2.如图,AB是⊙O的直径,点D是⊙O上一点OC为⊙O的半径,连接AD、CD.若∠D=40°,则∠COB的度数是( B )
A.110° B.100° C.140° D.120°
3.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D= 62 °.
4.一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为 26 厘米.
5.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= 75° .
6.如图,AB是圆O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=8,求圆O的半径.
【解答】(1)证明:连接AC,
∵AB⊥CD,AB过圆心O,
∴,
∴∠ACD=∠ADC,
由圆周角定理得:∠AGD=∠ACD,
∴∠ADC=∠AGD;
(2)解:连接OC,
∵AB⊥CD,AB过圆心O,CD=8,
∴CE=DE=4,
设⊙O的半径为R,则OC=OB=R,
由勾股定理得:OC2=CE2+OE2,
∴R2=42+(R﹣2)2,
解得:R=5,
即⊙O的半径是5.
A基础篇(10min)
1.下列说法,其中正确的有( )
①过圆心的线段是直径
②圆上的一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形
③大于半圆的弧叫做劣弧
④圆心相同,半径不等的圆叫做同心圆
A.1个 B.2个 C.3个 D.4个
2.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( )
A.4cm B.6cm C.8cm D.10cm
3.如图,在⊙O中,点C是的中点,若∠ABC=65°,则∠D的度数是( )
A.75° B.65° C.50° D.40°
4.如图,点A,B,C在⊙O上,为优弧,已知50°,则∠C为( )
A.25° B.35° C.40° D.50°
5.如图,AB是 O的直径,3,则∠BAC=( )
A.67.5° B.45° C.30° D.22.5°
6.如图,⊙O的内接四边形ABCD中,∠D=50°,则∠B为( )
A.140° B.130° C.120° D.100°
7.如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=15°,则∠BDC=( )
A.85° B.75° C.70° D.65°
8.如图,BD是⊙O的直径,A,C在圆上,∠A=50°,∠DBC的度数是( )
A.50° B.45° C.40° D.35°
9.如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为( )
A.138° B.121° C.118° D.112°
10.如图,已知∠ABC=60°,点D为BA边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段OB长为半径作弧,交BC于点E,连接DE,则BE的长是( )
A.5 B.5 C.5 D.5
11.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 .
12.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为2,OC=1,则弦AB的长为 .
13.已知正三角形ABC的弦心距为a,那么△ABC的周长是 .(用含a的式子表示).
14.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
15.如图,A、B、C、D是半径为4cm的⊙O上的四点,AC是直径,∠D=45°,则AB= cm.
B巩固篇(40min)
1.如图,四边形ABCD是⊙O的内接四边形,连接AO、OC,∠ABC=70°,AO∥CD,则∠OCD的度数为( )
A.40° B.50° C.60° D.70°
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于( )
A.120° B.125° C.135° D.150°
3.如图,AB为⊙O的直径,点C、D在⊙O上.若∠ACD==50°,则∠BAD的大小为( )
A.25° B.30° C.40° D.50°
4.如图,在△ABC中,∠C=90°,AB=10.若以点C为圆心,CA长为半径的圆恰好经过AB的中点D,则⊙C的半径为( )
A. B.8 C.6 D.5
5.如图,AB是⊙O的直径,C是弧AB的中点,点D在弧BC上,AC,BD的延长线交于点E,则∠AEB﹣∠BCD等于( )
A.30° B.45° C.55° D.60°
6.如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于( )
A.155° B.150° C.160° D.162°
7.如图,在扇形AOB中,点C在上,CD⊥OB于点D,且D为OB的中点,连接AB,AC,则∠BAC=( )
A.30° B.22.5° C.20° D.15°
8.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( )
A. B.1 C. D.2
9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC=30°,则CD的长为( )
A.5 B.2 C.4 D.
10.如图,在四边形ABCD中,AB=AC=AD=3,∠DBC=15°,∠BDC=30°,则点A到BD的距离是( )
A.3 B. C.2 D.
11.如图,AB是⊙O的直径,且CD⊥AB于E,若AE=1,∠D=30°,则AB= .
12.如图,⊙O的半径为9cm,AB是弦,OC⊥AB于点C,将劣弧AB沿弦AB折叠交于OC的中点D,则AB的长为 .
13.如图,在平面直角坐标系xOy中,直线y与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
14.在半径为13cm的圆内有两条互相平行的弦,一条弦长为24cm,另一条弦长为10cm,则这两条弦之间的距离为 cm.
15.如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,则∠AOC= 度.
16.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=32,则⊙O的半径为 .
17.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
18.如图,AB和OC分别是⊙O的直径和半径,∠BOC=60°,点P是直径AB上的一个动点,射线CP与⊙O相交于点Q,若△POQ是等腰三角形,则∠CPB= .
19.如图,BD是⊙O的直径,,点C是半圆上一动点,且与点A分别在BD的两侧.
(1)如图1,若5,BD=4,求AC的长;
(2)求证:CD+BCAC.
C提升篇
1.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
2.如图,弧AB所对的圆心角为∠AOB=120°,半径OB=2,C是OA的中点,P是弧AB上一动点,以CP为边作等边△CPQ(O,Q两点位于CP同侧),当P从A向B运动过程中,BQ的最小值为 .
3.如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
课后练习
1.如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=( )
A. B. C.1 D.2
2.如图,AB是⊙O的直径,点D是⊙O上一点OC为⊙O的半径,连接AD、CD.若∠D=40°,则∠COB的度数是( )
A.110° B.100° C.140° D.120°
3.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D= °.
4.一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为 厘米.
5.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= .
6.如图,AB是圆O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=8,求圆O的半径.
第24章 圆 分层练习(答案)
A基础篇(10min)
1.下列说法,其中正确的有( B )
①过圆心的线段是直径
②圆上的一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形
③大于半圆的弧叫做劣弧
④圆心相同,半径不等的圆叫做同心圆
A.1个 B.2个 C.3个 D.4个
2.如图,在⊙O中,OD⊥AB于点D,AD的长为3cm,则弦AB的长为( B )
A.4cm B.6cm C.8cm D.10cm
3.如图,在⊙O中,点C是的中点,若∠ABC=65°,则∠D的度数是( C )
A.75° B.65° C.50° D.40°
4.如图,点A,B,C在⊙O上,为优弧,已知50°,则∠C为( A )
A.25° B.35° C.40° D.50°
5.如图,AB是 O的直径,3,则∠BAC=( D )
A.67.5° B.45° C.30° D.22.5°
6.如图,⊙O的内接四边形ABCD中,∠D=50°,则∠B为( B )
A.140° B.130° C.120° D.100°
7.如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=15°,则∠BDC=( B )
A.85° B.75° C.70° D.65°
8.如图,BD是⊙O的直径,A,C在圆上,∠A=50°,∠DBC的度数是( C )
A.50° B.45° C.40° D.35°
9.如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为( C )
A.138° B.121° C.118° D.112°
10.如图,已知∠ABC=60°,点D为BA边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段OB长为半径作弧,交BC于点E,连接DE,则BE的长是( A )
A.5 B.5 C.5 D.5
11.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 4 .
12.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为2,OC=1,则弦AB的长为 2 .
13.已知正三角形ABC的弦心距为a,那么△ABC的周长是 6a .(用含a的式子表示).
14.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= 1.5 .
15.如图,A、B、C、D是半径为4cm的⊙O上的四点,AC是直径,∠D=45°,则AB= cm.
B巩固篇(40min)
1.如图,四边形ABCD是⊙O的内接四边形,连接AO、OC,∠ABC=70°,AO∥CD,则∠OCD的度数为( A )
A.40° B.50° C.60° D.70°
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于( A )
A.120° B.125° C.135° D.150°
3.如图,AB为⊙O的直径,点C、D在⊙O上.若∠ACD==50°,则∠BAD的大小为( C )
A.25° B.30° C.40° D.50°
4.如图,在△ABC中,∠C=90°,AB=10.若以点C为圆心,CA长为半径的圆恰好经过AB的中点D,则⊙C的半径为( D )
A. B.8 C.6 D.5
5.如图,AB是⊙O的直径,C是弧AB的中点,点D在弧BC上,AC,BD的延长线交于点E,则∠AEB﹣∠BCD等于( B )
A.30° B.45° C.55° D.60°
6.如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于( A )
A.155° B.150° C.160° D.162°
7.如图,在扇形AOB中,点C在上,CD⊥OB于点D,且D为OB的中点,连接AB,AC,则∠BAC=( A )
A.30° B.22.5° C.20° D.15°
8.如图,在⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是( A )
A. B.1 C. D.2
9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC=30°,则CD的长为( C )
A.5 B.2 C.4 D.
10.如图,在四边形ABCD中,AB=AC=AD=3,∠DBC=15°,∠BDC=30°,则点A到BD的距离是( B )
A.3 B. C.2 D.
11.如图,AB是⊙O的直径,且CD⊥AB于E,若AE=1,∠D=30°,则AB= 4 .
12.如图,⊙O的半径为9cm,AB是弦,OC⊥AB于点C,将劣弧AB沿弦AB折叠交于OC的中点D,则AB的长为 6cm .
13.如图,在平面直角坐标系xOy中,直线y与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 3 .
14.在半径为13cm的圆内有两条互相平行的弦,一条弦长为24cm,另一条弦长为10cm,则这两条弦之间的距离为 17或7 cm.
15.如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,则∠AOC= 125 度.
16.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=32,则⊙O的半径为 4 .
17.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
18.如图,AB和OC分别是⊙O的直径和半径,∠BOC=60°,点P是直径AB上的一个动点,射线CP与⊙O相交于点Q,若△POQ是等腰三角形,则∠CPB= 100°或40°或80° .
19.如图,BD是⊙O的直径,,点C是半圆上一动点,且与点A分别在BD的两侧.
(1)如图1,若5,BD=4,求AC的长;
(2)求证:CD+BCAC.
【解答】(1)解:连接CO并延长交⊙O于点E,连接AE,
∵BD是⊙O的直径,
∴∠BAD=90°,
∵,
∴AB=AD,
∴∠ADB=∠ABD=45°,
∵5,
∴∠BOC∠COD,
∴∠BOC∠BOD=180°30°,
∴∠BDC∠BOC=15°,
∴∠ADC=∠ADB+∠BDC=60°,
∴∠ADC=∠AEC=60°,
∵CE是⊙O的直径,
∴∠CAE=90°,
∵CE=BD=4,
∴AC=CEsin60°=42;
(2)证明:过点A作FA⊥AC,交CD的延长线于点F,
∴∠CAF=90°,
∵∠BAD=90°,
∴∠BAD﹣∠CAD=∠CAF﹣∠CAD,
∴∠BAC=∠DAF,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADF=180°,
∴∠ADF=∠ABC,
∵AB=AD,
∴△ABC≌△ADF(ASA),
∴AC=AF,BC=DF,
∴△ACF是等腰直角三角形,
∴CFAC,
∴CD+DFAC,
∴CD+BCAC.
C提升篇
1.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( C )
A.4 B.5 C.6 D.7
2.如图,弧AB所对的圆心角为∠AOB=120°,半径OB=2,C是OA的中点,P是弧AB上一动点,以CP为边作等边△CPQ(O,Q两点位于CP同侧),当P从A向B运动过程中,BQ的最小值为 1 .
3.如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
课后练习
1.如图,AB为⊙O的直径,弦CD交AB于点E,,∠CDB=30°,AC=2,则OE=( C )
A. B. C.1 D.2
2.如图,AB是⊙O的直径,点D是⊙O上一点OC为⊙O的半径,连接AD、CD.若∠D=40°,则∠COB的度数是( B )
A.110° B.100° C.140° D.120°
3.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D= 62 °.
4.一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为 26 厘米.
5.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= 75° .
6.如图,AB是圆O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=8,求圆O的半径.
【解答】(1)证明:连接AC,
∵AB⊥CD,AB过圆心O,
∴,
∴∠ACD=∠ADC,
由圆周角定理得:∠AGD=∠ACD,
∴∠ADC=∠AGD;
(2)解:连接OC,
∵AB⊥CD,AB过圆心O,CD=8,
∴CE=DE=4,
设⊙O的半径为R,则OC=OB=R,
由勾股定理得:OC2=CE2+OE2,
∴R2=42+(R﹣2)2,
解得:R=5,
即⊙O的半径是5.
同课章节目录
