人教版数学八年级上册 第十二章第16课时 角的平分线的性质(一)课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 第十二章第16课时 角的平分线的性质(一)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 16:23:11 | ||
图片预览




文档简介
(共20张PPT)
第十二章 全等三角形
第16课时 角的平分线的性质(一)
目录
01
本课目标
02
课堂导练
1.会用尺规作一个角的平分线,知道作法的合理性.
2.探索并证明角的平分线的性质.
3.能应用角的平分线的性质解决相关问题.
本课目标
知识重点
知识点一:尺规作图——作已知角的平分线
已知∠AOB,作射线OC,使得OC平分∠AOB.作图步骤如下:
①以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E;
②分别以点D,E为圆心,_____________的长为半径在角的内部画弧,两弧交于点C;
③画射线OC,射线OC即为________的平分线.
∠AOB
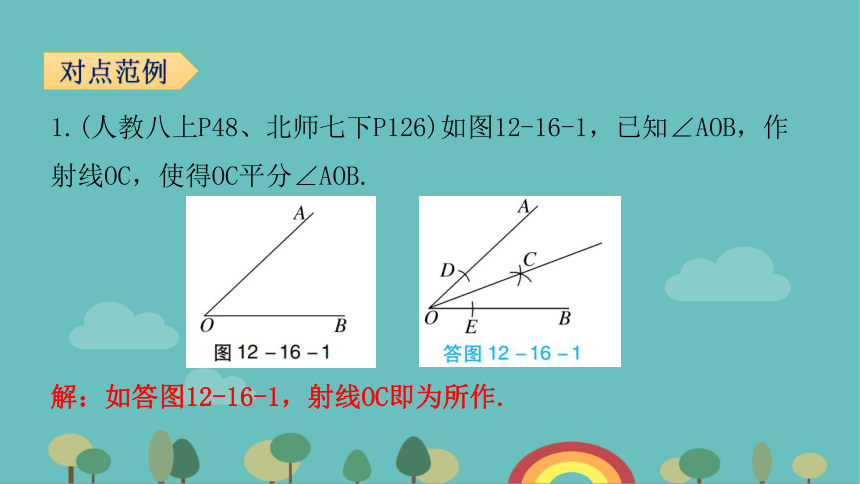
1.(人教八上P48、北师七下P126)如图12-16-1,已知∠AOB,作射线OC,使得OC平分∠AOB.
对点范例
解:如答图12-16-1,射线OC即为所作.
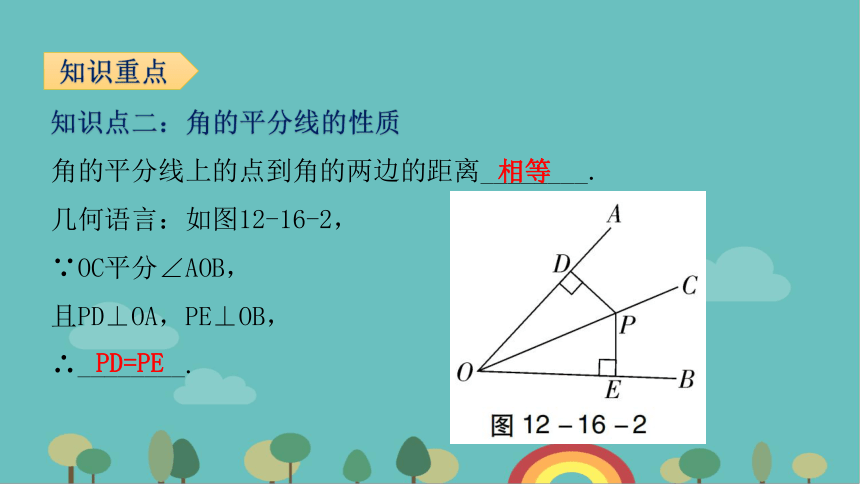
知识点二:角的平分线的性质
角的平分线上的点到角的两边的距离________.
几何语言:如图12-16-2,
∵OC平分∠AOB,
且PD⊥OA,PE⊥OB,
∴________.
知识重点
相等
PD=PE
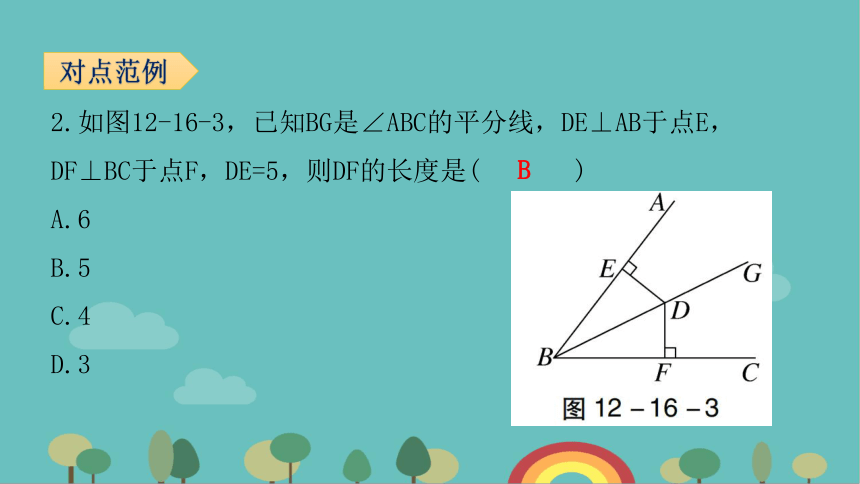
2.如图12-16-3,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=5,则DF的长度是( )
A.6
B.5
C.4
D.3
对点范例
B
课堂导练
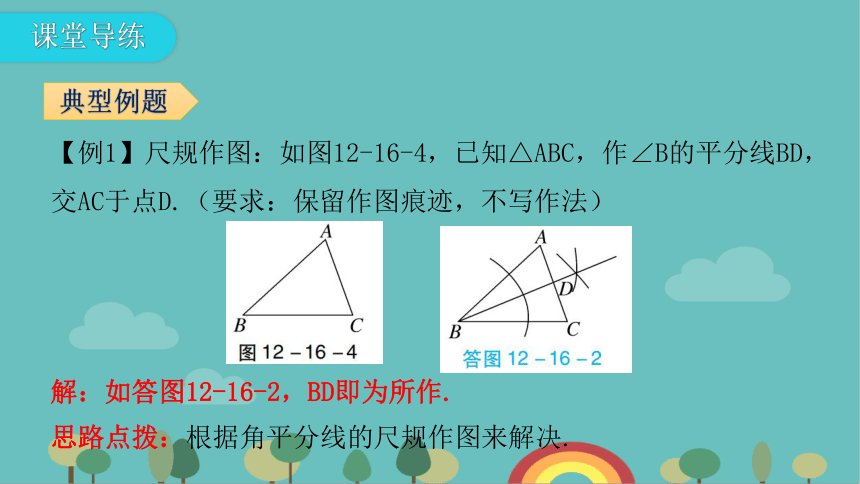
【例1】尺规作图:如图12-16-4,已知△ABC,作∠B的平分线BD,交AC于点D.(要求:保留作图痕迹,不写作法)
典型例题
解:如答图12-16-2,BD即为所作.
思路点拨:根据角平分线的尺规作图来解决.
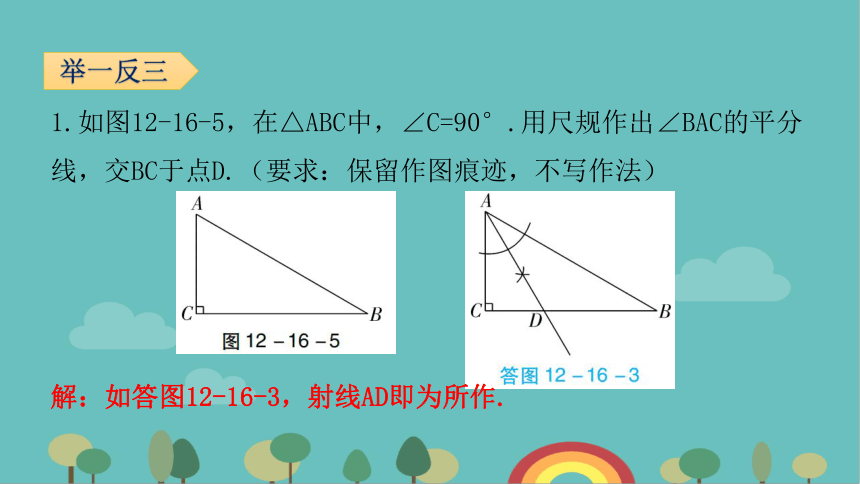
1.如图12-16-5,在△ABC中,∠C=90°.用尺规作出∠BAC的平分线,交BC于点D.(要求:保留作图痕迹,不写作法)
举一反三
解:如答图12-16-3,射线AD即为所作.
【例2】如图12-16-6,OP平分∠AOB,PC⊥OA,点D是OB上的动点.若PC=5 cm,则PD的长可以是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
思路点拨:根据角平分线的性质可知PD的
长的最小值,再逐个判断即可.
典型例题
D
2.如图12-16-7,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,DE=5,BD=2CD,则BC的长为________.
举一反三
15
【例3】如图12-16-8,在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E.若BC=5,DE=2,则△BCE的面积为( )
A.4 B.5
C.7 D.10
思路点拨:根据角平分线的性质可以得出
△BCE的高,再根据三角形的面积公式求
解即可.
典型例题
B
3.如图12-16-9,AD是∠BAC的平分线,DE⊥AB于点E,若S△ABC=10,DE=2,AB=6,则AC长是( )
A.3
B.4
C.5
D.6
举一反三
B
【例4】(人教八上P51改编、北师八下P30改编)如图12-16-10,在△ABC中,AD平分∠BAC,且DE⊥AB,DF⊥AC,已知S△ABC=27 cm2,AB=10 cm,AC=8 cm.
(1)求证:AE=AF;
(2)求DE的长.
典型例题
思路点拨:(1)利用角平分线的性质,则可根据“HL”判定三角形全等,进而得出结论;(2)结合(1),可根据三角形的面积公式来解题.
4.(提升题)如图12-16-11,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BE=FC.
(1)求证:BD=DF;
(2)判断BE,AF和AE之间的数量关系,
并说明理由.
举一反三
谢 谢
第十二章 全等三角形
第16课时 角的平分线的性质(一)
目录
01
本课目标
02
课堂导练
1.会用尺规作一个角的平分线,知道作法的合理性.
2.探索并证明角的平分线的性质.
3.能应用角的平分线的性质解决相关问题.
本课目标
知识重点
知识点一:尺规作图——作已知角的平分线
已知∠AOB,作射线OC,使得OC平分∠AOB.作图步骤如下:
①以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E;
②分别以点D,E为圆心,_____________的长为半径在角的内部画弧,两弧交于点C;
③画射线OC,射线OC即为________的平分线.
∠AOB
1.(人教八上P48、北师七下P126)如图12-16-1,已知∠AOB,作射线OC,使得OC平分∠AOB.
对点范例
解:如答图12-16-1,射线OC即为所作.
知识点二:角的平分线的性质
角的平分线上的点到角的两边的距离________.
几何语言:如图12-16-2,
∵OC平分∠AOB,
且PD⊥OA,PE⊥OB,
∴________.
知识重点
相等
PD=PE
2.如图12-16-3,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=5,则DF的长度是( )
A.6
B.5
C.4
D.3
对点范例
B
课堂导练
【例1】尺规作图:如图12-16-4,已知△ABC,作∠B的平分线BD,交AC于点D.(要求:保留作图痕迹,不写作法)
典型例题
解:如答图12-16-2,BD即为所作.
思路点拨:根据角平分线的尺规作图来解决.
1.如图12-16-5,在△ABC中,∠C=90°.用尺规作出∠BAC的平分线,交BC于点D.(要求:保留作图痕迹,不写作法)
举一反三
解:如答图12-16-3,射线AD即为所作.
【例2】如图12-16-6,OP平分∠AOB,PC⊥OA,点D是OB上的动点.若PC=5 cm,则PD的长可以是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
思路点拨:根据角平分线的性质可知PD的
长的最小值,再逐个判断即可.
典型例题
D
2.如图12-16-7,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,DE=5,BD=2CD,则BC的长为________.
举一反三
15
【例3】如图12-16-8,在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E.若BC=5,DE=2,则△BCE的面积为( )
A.4 B.5
C.7 D.10
思路点拨:根据角平分线的性质可以得出
△BCE的高,再根据三角形的面积公式求
解即可.
典型例题
B
3.如图12-16-9,AD是∠BAC的平分线,DE⊥AB于点E,若S△ABC=10,DE=2,AB=6,则AC长是( )
A.3
B.4
C.5
D.6
举一反三
B
【例4】(人教八上P51改编、北师八下P30改编)如图12-16-10,在△ABC中,AD平分∠BAC,且DE⊥AB,DF⊥AC,已知S△ABC=27 cm2,AB=10 cm,AC=8 cm.
(1)求证:AE=AF;
(2)求DE的长.
典型例题
思路点拨:(1)利用角平分线的性质,则可根据“HL”判定三角形全等,进而得出结论;(2)结合(1),可根据三角形的面积公式来解题.
4.(提升题)如图12-16-11,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BE=FC.
(1)求证:BD=DF;
(2)判断BE,AF和AE之间的数量关系,
并说明理由.
举一反三
谢 谢
