18.2《特殊的平行四边形》复习课 课件(共20张PPT)
文档属性
| 名称 | 18.2《特殊的平行四边形》复习课 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:56:09 | ||
图片预览



文档简介
(共20张PPT)
《特殊的平行四边形》复习课
八年级数学下(RJ)
1、掌握矩形、菱形、正方形的定义、性质和判定;
2、理解平行四边形、特殊平行四边形的联系与区别,能利用它们的性质和判定进行推理和计算;
3、使学生明确知识体系,提高空间想象能力,掌握基本的推理能力。
复习目标:
教学重点、难点:
重点:掌握特殊平行四边形性质与判定。
难点:能用特殊平行四边形的判定定理和性质定理进行几何证明和计算。
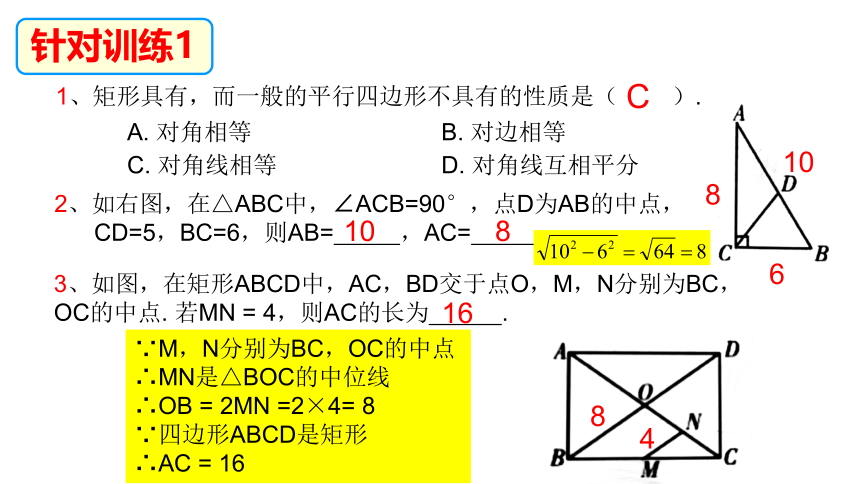
性质 判定
边 ①两组对边分别 ; ②两组对边分别 ; 有一个角是直角的 是矩形
角 矩形的四个角都是 ; 有三个角是直角的四边形是矩形
对角线 矩形的两条对角线 . 的平行四边形是矩形
知识梳理1
矩形
轴对称图形
2条对称轴
平行
相等
直角
平行四边形
对角线相等
推论:直角三角形斜边上的中线等于斜边的一半.
相等
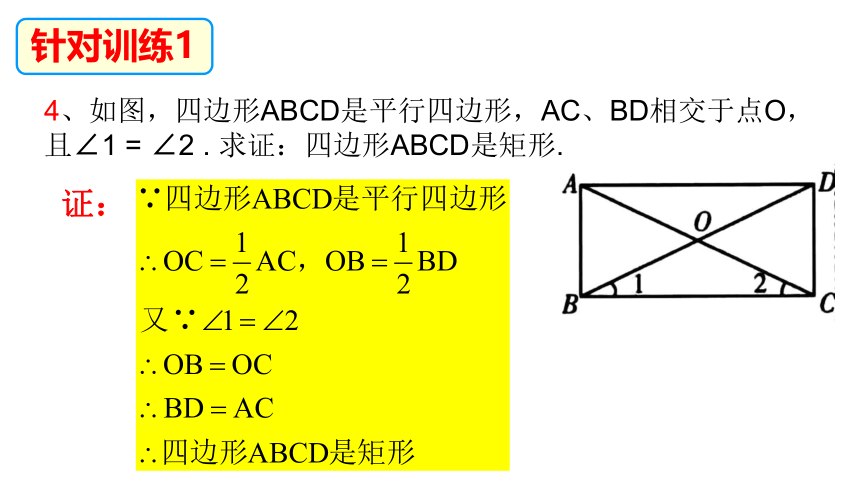
针对训练1
1、矩形具有,而一般的平行四边形不具有的性质是( ).
3、如图,在矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点. 若MN = 4,则AC的长为 .
A. 对角相等
B. 对边相等
C. 对角线相等
D. 对角线互相平分
C
16
∵M,N分别为BC,OC的中点
∴MN是△BOC的中位线
∴OB = 2MN =2×4= 8
∵四边形ABCD是矩形
∴AC = 16
2、如右图,在△ABC中,∠ACB=90°,点D为AB的中点,
CD=5,BC=6,则AB= ,AC= .
10
8
10
6
8
8
4
针对训练1
4、如图,四边形ABCD是平行四边形,AC、BD相交于点O,且∠1 = ∠2 . 求证:四边形ABCD是矩形.
证:
性质 判定
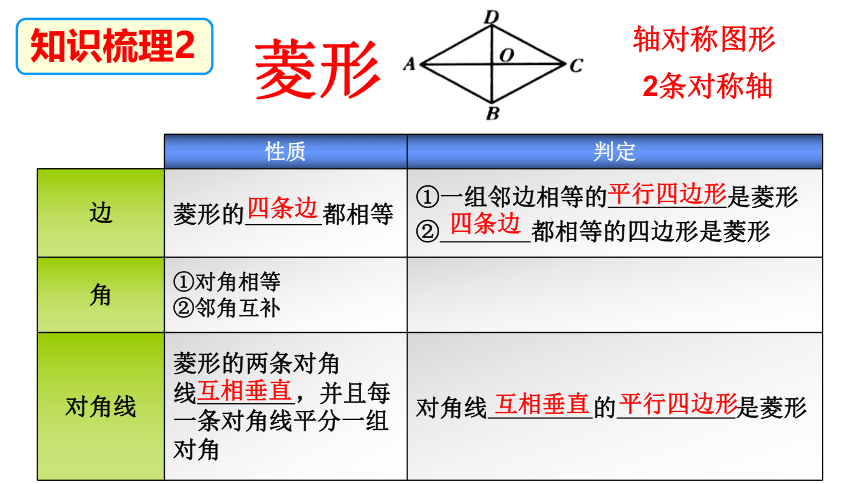
边 菱形的 都相等 ①一组邻边相等的 是菱形
② 都相等的四边形是菱形
角 ①对角相等 ②邻角互补
对角线 菱形的两条对角线 ,并且每一条对角线平分一组对角 对角线 的 是菱形
知识梳理2
菱形
轴对称图形
2条对称轴
四条边
平行四边形
四条边
互相垂直
互相垂直
平行四边形
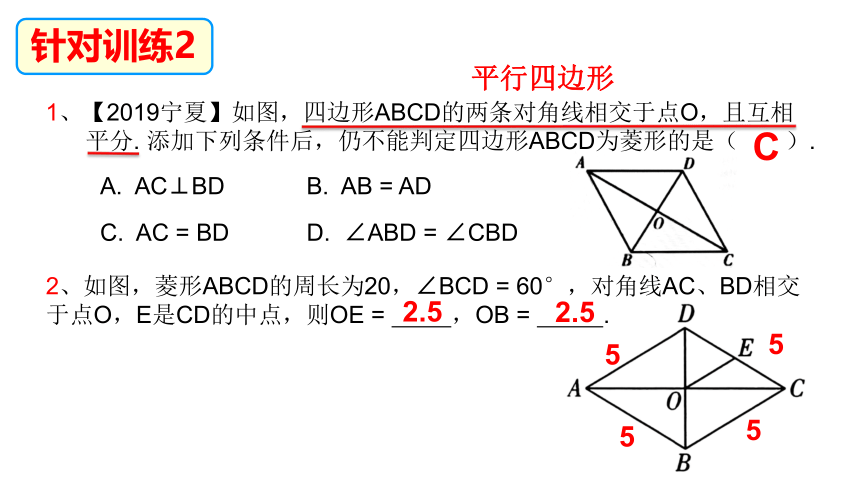
针对训练2
1、【2019宁夏】如图,四边形ABCD的两条对角线相交于点O,且互相
平分. 添加下列条件后,仍不能判定四边形ABCD为菱形的是( ).
A. AC⊥BD
B. AB = AD
C. AC = BD
D. ∠ABD = ∠CBD
C
2、如图,菱形ABCD的周长为20,∠BCD = 60°,对角线AC、BD相交于点O,E是CD的中点,则OE = ,OB = .
2.5
2.5
5
5
5
5
平行四边形
针对训练2
3、【2019·兰州】如图,AC = 8,分别以A,C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D. 依次连接A,B,C,D,连接BD交AC于点O.
(1)判断四边形ABCD的形状并说明理由;
(2)求BD的长.
(1)四边形ABCD是菱形
证:由作法得AB=AD=CB=CD=5
所以四边形ABCD是菱形
(2)∵四边形ABCD是菱形
∴ ,OB=OD,AC⊥BD
在Rt△AOB中,
∴BD=2OB=6
继续思考:四边形ABCD的面积是多少?
5
4
3
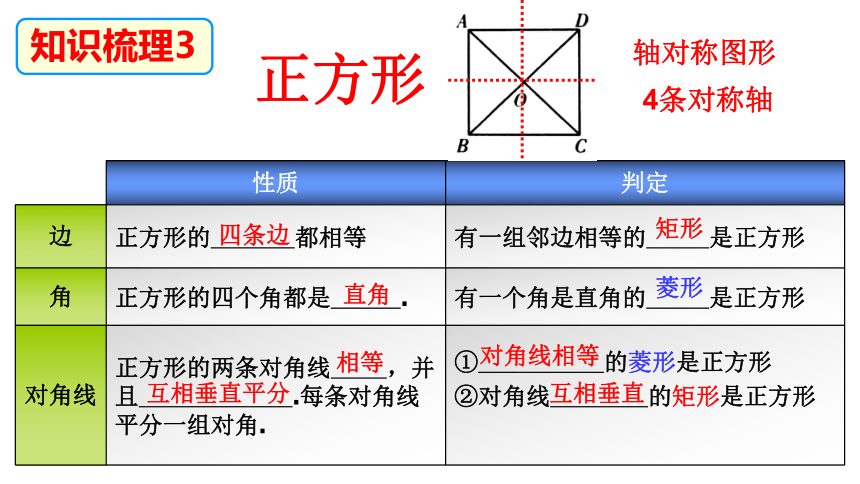
性质 判定
边 正方形的 都相等 有一组邻边相等的 是正方形
角 正方形的四个角都是 . 有一个角是直角的 是正方形
对角线 正方形的两条对角线 ,并且 .每条对角线平分一组对角. ① 的菱形是正方形
②对角线 的矩形是正方形
知识梳理3
正方形
轴对称图形
4条对称轴
四条边
直角
相等
互相垂直平分
矩形
菱形
对角线相等
互相垂直
针对训练3
1、如图,已知正方形的边长为4cm,则其对角线长是( ).
A. 8cm
B. 16cm
C. 32cm
D. cm
D
2、【2016广东】如图,正方形ABCD的面积为1,则以相邻两边中点的连
线EF为边的正方形EFGH的周长为( ).
A.
B.
C.
D.
B
针对训练3
3、如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,
CD上,且∠CEF = 45°. 求证:矩形ABCD是正方形.
证:∵四边形ABCD是矩形
∴∠B = ∠D = ∠C =90°
∵△AEF是等边三角形
∴AE = AF,∠AEF = ∠AFE = 60°
∵∠CEF = 45°
∴∠CFE = ∠CEF = 45°
∴∠AFD = ∠AEB = 180°- 45°- 60°= 75°
∴△AEB≌△AFD(AAS)
∴AB = AD
∴矩形ABCD是正方形.
综合训练
证明:∵DP∥OC,DP=OC
∴四边形CODP是平行四边形.
∵四边形ABCD是矩形,
∴CO=DO.
∴四边形CODP是菱形.
问题:如图,矩形ABCD的对角线AC、BD交于点O,过点D作
DP∥OC,且DP=OC,连结CP. 试判断四边形CODP的形状.
结论:四边形CODP是菱形
一组邻边相等的平行四边形是菱形.
变式1:如图,菱形ABCD的对角线AC、BD交于点O,过点D作
DP∥OC,且DP=OC,连结CP. 试判断四边形CODP的形状.
证明:∵DP∥OC,DP=OC
∴四边形CODP是平行四边形
∵四边形ABCD是菱形
∴OC⊥OD
∴∠COD = 90°
∴四边形CODP是矩形
结论:四边形CODP是矩形
综合训练
有一个角是直角的平行四边形是矩形.
变式2:如图,正方形ABCD的对角线AC、BD交于点O,过点D作
DP∥OC,且DP=OC,连结CP. 试判断四边形CODP的形状.
P
C
D
O
B
A
证明:∵DP∥OC,DP=OC
∴四边形CODP是平行四边形
∵四边形ABCD是正方形
∴CO⊥DO,CO=DO
∴四边形CODP是正方形
结论:四边形CODP是正方形
综合训练
一组邻边相等的矩形是正方形.
有一个角是直角的平行四边形是矩形.
平行四边形
矩形
菱形
正方形
有一个角是直角
有一组邻边相等并且有一个角是直角
有一个角是直角
有一组邻边相等
有一组邻边相等
平行四边形、矩形、菱形、正方形之间的联系
回顾小结
回顾小结
平行四边形、矩形、菱形、正方形之间的联系
平行四边形
矩形
菱形
正方形
1、下列说法正确的有( ).
①四边都相等的四边形是正方形
②四个内角都相等的四边形是正方形
③有三个角是直角,且有一组邻边相等的四边形是正方形
④有一个角是直角的平行四边形是正方形
A.1个 B.2个 C.3个 D.4个
达标检测
A
×
×
×
√
菱形
矩形
矩形
2、如图,菱形ABCD的对角线相交于点O,请你添加一个条
件: ,使得该菱形为正方形.
∠BAD=90°
BD = AC
有一个角是直角的菱形是正方形;
对角线相等的菱形是正方形.
3、【2012临沂】如图,点A、F、C、D在同一直线上,点B和点E分别往直
线AD的两侧,且AB=DE,∠A=∠D,AF=DC,BE⊥FC.
求证:四边形BCEF是菱形.
证明:∵AF=DC,
∴AF+FC=DC+FC,即AC=DF.
又∵∠A=∠D,AB=DE
∴△ABC≌△DEF(SAS)
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形
∵BE⊥FC
∴四边形BCEF是菱形.
达标检测
布置作业
顺次连接任意四边形各边的中点,所构成的四边形称为“中点四边形”. 试判断中点四边形EFGH的形状,并说明理由。
(1)若AC=BD,判断四边形EFGH的形状;
(2)若AC⊥BD,判断四边形EFGH的形状;
(3)添加一个条件,使四边形EFGH为正方形,并写证明过程.
谢谢,再见
祝愿学业有成
《特殊的平行四边形》复习课
八年级数学下(RJ)
1、掌握矩形、菱形、正方形的定义、性质和判定;
2、理解平行四边形、特殊平行四边形的联系与区别,能利用它们的性质和判定进行推理和计算;
3、使学生明确知识体系,提高空间想象能力,掌握基本的推理能力。
复习目标:
教学重点、难点:
重点:掌握特殊平行四边形性质与判定。
难点:能用特殊平行四边形的判定定理和性质定理进行几何证明和计算。
性质 判定
边 ①两组对边分别 ; ②两组对边分别 ; 有一个角是直角的 是矩形
角 矩形的四个角都是 ; 有三个角是直角的四边形是矩形
对角线 矩形的两条对角线 . 的平行四边形是矩形
知识梳理1
矩形
轴对称图形
2条对称轴
平行
相等
直角
平行四边形
对角线相等
推论:直角三角形斜边上的中线等于斜边的一半.
相等
针对训练1
1、矩形具有,而一般的平行四边形不具有的性质是( ).
3、如图,在矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点. 若MN = 4,则AC的长为 .
A. 对角相等
B. 对边相等
C. 对角线相等
D. 对角线互相平分
C
16
∵M,N分别为BC,OC的中点
∴MN是△BOC的中位线
∴OB = 2MN =2×4= 8
∵四边形ABCD是矩形
∴AC = 16
2、如右图,在△ABC中,∠ACB=90°,点D为AB的中点,
CD=5,BC=6,则AB= ,AC= .
10
8
10
6
8
8
4
针对训练1
4、如图,四边形ABCD是平行四边形,AC、BD相交于点O,且∠1 = ∠2 . 求证:四边形ABCD是矩形.
证:
性质 判定
边 菱形的 都相等 ①一组邻边相等的 是菱形
② 都相等的四边形是菱形
角 ①对角相等 ②邻角互补
对角线 菱形的两条对角线 ,并且每一条对角线平分一组对角 对角线 的 是菱形
知识梳理2
菱形
轴对称图形
2条对称轴
四条边
平行四边形
四条边
互相垂直
互相垂直
平行四边形
针对训练2
1、【2019宁夏】如图,四边形ABCD的两条对角线相交于点O,且互相
平分. 添加下列条件后,仍不能判定四边形ABCD为菱形的是( ).
A. AC⊥BD
B. AB = AD
C. AC = BD
D. ∠ABD = ∠CBD
C
2、如图,菱形ABCD的周长为20,∠BCD = 60°,对角线AC、BD相交于点O,E是CD的中点,则OE = ,OB = .
2.5
2.5
5
5
5
5
平行四边形
针对训练2
3、【2019·兰州】如图,AC = 8,分别以A,C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D. 依次连接A,B,C,D,连接BD交AC于点O.
(1)判断四边形ABCD的形状并说明理由;
(2)求BD的长.
(1)四边形ABCD是菱形
证:由作法得AB=AD=CB=CD=5
所以四边形ABCD是菱形
(2)∵四边形ABCD是菱形
∴ ,OB=OD,AC⊥BD
在Rt△AOB中,
∴BD=2OB=6
继续思考:四边形ABCD的面积是多少?
5
4
3
性质 判定
边 正方形的 都相等 有一组邻边相等的 是正方形
角 正方形的四个角都是 . 有一个角是直角的 是正方形
对角线 正方形的两条对角线 ,并且 .每条对角线平分一组对角. ① 的菱形是正方形
②对角线 的矩形是正方形
知识梳理3
正方形
轴对称图形
4条对称轴
四条边
直角
相等
互相垂直平分
矩形
菱形
对角线相等
互相垂直
针对训练3
1、如图,已知正方形的边长为4cm,则其对角线长是( ).
A. 8cm
B. 16cm
C. 32cm
D. cm
D
2、【2016广东】如图,正方形ABCD的面积为1,则以相邻两边中点的连
线EF为边的正方形EFGH的周长为( ).
A.
B.
C.
D.
B
针对训练3
3、如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,
CD上,且∠CEF = 45°. 求证:矩形ABCD是正方形.
证:∵四边形ABCD是矩形
∴∠B = ∠D = ∠C =90°
∵△AEF是等边三角形
∴AE = AF,∠AEF = ∠AFE = 60°
∵∠CEF = 45°
∴∠CFE = ∠CEF = 45°
∴∠AFD = ∠AEB = 180°- 45°- 60°= 75°
∴△AEB≌△AFD(AAS)
∴AB = AD
∴矩形ABCD是正方形.
综合训练
证明:∵DP∥OC,DP=OC
∴四边形CODP是平行四边形.
∵四边形ABCD是矩形,
∴CO=DO.
∴四边形CODP是菱形.
问题:如图,矩形ABCD的对角线AC、BD交于点O,过点D作
DP∥OC,且DP=OC,连结CP. 试判断四边形CODP的形状.
结论:四边形CODP是菱形
一组邻边相等的平行四边形是菱形.
变式1:如图,菱形ABCD的对角线AC、BD交于点O,过点D作
DP∥OC,且DP=OC,连结CP. 试判断四边形CODP的形状.
证明:∵DP∥OC,DP=OC
∴四边形CODP是平行四边形
∵四边形ABCD是菱形
∴OC⊥OD
∴∠COD = 90°
∴四边形CODP是矩形
结论:四边形CODP是矩形
综合训练
有一个角是直角的平行四边形是矩形.
变式2:如图,正方形ABCD的对角线AC、BD交于点O,过点D作
DP∥OC,且DP=OC,连结CP. 试判断四边形CODP的形状.
P
C
D
O
B
A
证明:∵DP∥OC,DP=OC
∴四边形CODP是平行四边形
∵四边形ABCD是正方形
∴CO⊥DO,CO=DO
∴四边形CODP是正方形
结论:四边形CODP是正方形
综合训练
一组邻边相等的矩形是正方形.
有一个角是直角的平行四边形是矩形.
平行四边形
矩形
菱形
正方形
有一个角是直角
有一组邻边相等并且有一个角是直角
有一个角是直角
有一组邻边相等
有一组邻边相等
平行四边形、矩形、菱形、正方形之间的联系
回顾小结
回顾小结
平行四边形、矩形、菱形、正方形之间的联系
平行四边形
矩形
菱形
正方形
1、下列说法正确的有( ).
①四边都相等的四边形是正方形
②四个内角都相等的四边形是正方形
③有三个角是直角,且有一组邻边相等的四边形是正方形
④有一个角是直角的平行四边形是正方形
A.1个 B.2个 C.3个 D.4个
达标检测
A
×
×
×
√
菱形
矩形
矩形
2、如图,菱形ABCD的对角线相交于点O,请你添加一个条
件: ,使得该菱形为正方形.
∠BAD=90°
BD = AC
有一个角是直角的菱形是正方形;
对角线相等的菱形是正方形.
3、【2012临沂】如图,点A、F、C、D在同一直线上,点B和点E分别往直
线AD的两侧,且AB=DE,∠A=∠D,AF=DC,BE⊥FC.
求证:四边形BCEF是菱形.
证明:∵AF=DC,
∴AF+FC=DC+FC,即AC=DF.
又∵∠A=∠D,AB=DE
∴△ABC≌△DEF(SAS)
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形
∵BE⊥FC
∴四边形BCEF是菱形.
达标检测
布置作业
顺次连接任意四边形各边的中点,所构成的四边形称为“中点四边形”. 试判断中点四边形EFGH的形状,并说明理由。
(1)若AC=BD,判断四边形EFGH的形状;
(2)若AC⊥BD,判断四边形EFGH的形状;
(3)添加一个条件,使四边形EFGH为正方形,并写证明过程.
谢谢,再见
祝愿学业有成
