2022-2023学年高一上学期数学人教A版(2019)必修第一册3.3幂函数课件(23张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册3.3幂函数课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览








文档简介
幂函数
知识目标
1.了解幂函数的概念,会求幂函数的解析式.
2.通过具体实例,结合????=????,????=????????,????=????????,
????=?????????,????=????????????的图象理解它们的变化规律,了解幂函数.
?
核心素养目标
以五个常见幂函数为载体,归纳幂函数的图象与性质,发展数学抽象、逻辑推理的核心素养.
重 点:
五个幂函数的图像与性质
难 点:
画出????=????3和????=????12的图像,通过五个幂函数图像概括出它们的共性
?
前面学习了函数的概念,利用函数概念和对图像的观察(数形结合),研究了函数的一些性质。
本节我们利用这些知识研究一些新的函数.
首先让我们回顾前面都学习了函数的哪些性质
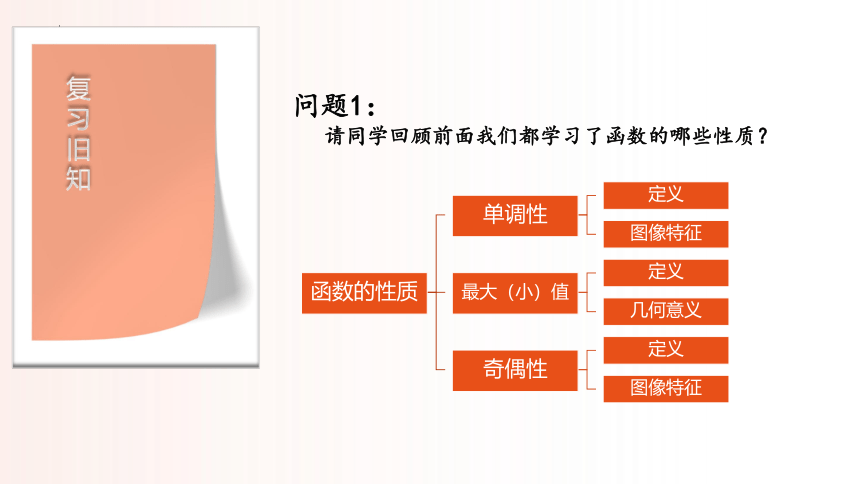
问题1:
请同学回顾前面我们都学习了函数的哪些性质?
函数的性质
单调性
定义
图像特征
最大(小)值
定义
几何意义
奇偶性
定义
图像特征
问题2
观察下列5个实例,概括出它们的解析式有什么异同点?
(1)如果张红以1元/????????的价格购买了某种蔬菜????????????,那么她需要支付????=????元,这里????是????的函数;
(2)如果正方形的边长为????,那么正方形的面积????=????????,这里????是????的函数;
(3)如果立方体的棱长为????,那么立方体的体积????=????????,这里????是????的函数;
?
(4)如果一个正方形场地的面积为????,那么这个正方形场地的边长????=????(????也可以表示为????????????) ,这里????是????的函数;
(5)如果某人?????????内骑车行进了????????????,那么他骑车的平均速度????=????????????????/????,即????=?????????,这里????是????的函数.
?
追问2-1.上述五个例子中的函数
????=?????,????=????????,????=????????.,
?????????????????????=????即????=????????????, ????=????????,即????=?????????
在结构形式上都有什么共同特征?
?
追问2-2.每个函数中的自变量都处在函数表达式中的什么位置?指数中含有变量吗?
小结汇总讨论成果
这些函数的解析式都有幂的形式,而且都是以幂的底数为自变量;幂的指数都是常数.
追问2-3.如果将上述五个函数中的自变量统一用????表示,因变量用y表示,请你将它们分别表示出来.
?
????=?????, ????=????????,????????=????????.??????????=????????????, ????=?????????
?
追问2-4. 上述五个函数能否统一表示为????=????????(????为常数).
?
一般地,函数????=????????叫做幂函数,其中????是自变量,????是常数.
?
1.下列函数是幂函数的是(????)
A. ????=2???? B. ????=????2?1 C. ????=????3 D.????=2????
?
2.若函数????=????????+????2?5????+6是幂函数,且是奇函数,则????=(????)
A. 1 B. 2 C. 3 D. 4
?
解:根据形如????=?????????(????为常数)的函数为幂函数,故选C
?
解:因为函数是幂函数,则????2?5????+6=0,可得????=2或????=3.
又因为函数是奇函数,
当????=2时,????2为偶函数(舍);
当????=3时,????3为奇函数,符合题意.
?
3.若幂函数f(x)的图象经过点(3,33),则其定义域为 ( )
A. {????|????∈????且????>0} B. {????|????∈????且????<0}
C. {????|????∈????且????≠0} D. ????
?
解:∵????(????)为幂函数,∴设????(????)=????????
又????(????)的图像经过点(3,33),
∴33=3????,解得:????=?12,∴????(????)=?????12=1????,
∴????(????)的定义域为{????|????∈????且????>0}.
?
问题3:现在我们掌握了幂函数的解析式,接着我们继续探究幂函数的性质,我们可以用什么方法呢?
追问3-1. 前面我们用了什么方法探究“一元二次不等式的解法、函数单调性及奇偶性”呢 ?
请你在同一坐标系中画出上述五个函数图像.
问题4:我们如何画出函数????=????3和????=????12的图像呢?
?
追问4-1.可以用描点法画函数????=????3和????=????12的图像吗?
?
追问4-1.可以用描点法画函数y=x3和y=x12的图像吗?
?
追问4-2. 函数y=x3和y=x12的定义域是什么?
?
追问4-3. 函数y=x3和y=x12的奇偶性是什么?
?
追问4-4. 函数y=x3和y=x12的单调性是什么?
?
讨论成果汇总:
y=x3定义域为R,是奇函数且在R上严格单调递增
?
讨论成果汇总:
y=x3定义域为R,是奇函数且在R上严格单调递增
????=????12定义域为(0,+∞),是非奇非偶函数且在(0,+∞)上严格单调递增
?
追问4-5.你能根据y=x3和y=x12的性质画出它们的图像吗?
?
经过上述的讨论,最终得到五个函数在同一坐标系中的图像,如图所示.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????=????3
????=????????
????=????
????=????????????
????=?????????
定义域
值 域
奇偶性
单调性
问题五:观察五个函数图像,它们有哪些共同性质?
有哪些不同性质?并将它们填入下表.
(1)定点:所有的幂函数在(????,+∞)都有定义,并且图象都过点(????,????)
(2)单调性:当?????>????时,在区间[????,+∞)上是增函数
当????<????时,幂函数在区间(????,+∞)上是减函数.
(3)奇偶性:
当α为奇数时,幂函数为奇函数
当α为偶数时,幂函数为偶函数
?
(4)幂函数????=????????的图象分布与幂指数α的关系具有如下规律:在直线x=1的右侧,按“逆时针”方向,图象所对应的幂指数依次增大(如图).
?
如图,①②③④对应四个幂函数的图象,其中②对应的幂函数是.( )
????=????3 B. ????=????2
C. ????=???? D. ????=????
?
解:根据幂函数的图象以及性质以及选项得:
①是????=????,②是????=????,③是????=????2,④是????=????3.
故选:????.
?
2.下列关于幂函数的图象和性质的描述中正确的有 ( )
幂函数的图象都过点(1,1)
B. 幂函数的图象都不经过第四象限
C. 幂函数必定是奇函数或偶函数中的一种
D. 幂函数必定是增函数或减函数中的一种
解:由幂函数的图象可知????,B正确;
对于????、存在幂函数????=????是非奇非偶函数,故C错误;
对于????、存在幂函数????=????0不具有单调性,故D错误,
故选AB.
?
3.已知????????=????12, 若0 A. ????(????)C. ????(????)
?
解:因为0又函数????(????)=????12在(0,+∞)上单调递增.
所以????(????)?
4.证明幂函数????(????)=????是增函数.
?
证明:函数的定义域是[????,+∞).
?????????,????????∈[????,+∞),且???????? ?????????????????????????=?????????????????
=(?????????????????)(????????+????????)????????+????????
=?????????????????????????+????????
∵?????????????????????,
∴????(????????)?
(1)幂函数的概念;
(2)5个常见幂函数的图象及其性质;
(3)幂函数的性质;
(4)幂函数比较大小的方法.
知识目标
1.了解幂函数的概念,会求幂函数的解析式.
2.通过具体实例,结合????=????,????=????????,????=????????,
????=?????????,????=????????????的图象理解它们的变化规律,了解幂函数.
?
核心素养目标
以五个常见幂函数为载体,归纳幂函数的图象与性质,发展数学抽象、逻辑推理的核心素养.
重 点:
五个幂函数的图像与性质
难 点:
画出????=????3和????=????12的图像,通过五个幂函数图像概括出它们的共性
?
前面学习了函数的概念,利用函数概念和对图像的观察(数形结合),研究了函数的一些性质。
本节我们利用这些知识研究一些新的函数.
首先让我们回顾前面都学习了函数的哪些性质
问题1:
请同学回顾前面我们都学习了函数的哪些性质?
函数的性质
单调性
定义
图像特征
最大(小)值
定义
几何意义
奇偶性
定义
图像特征
问题2
观察下列5个实例,概括出它们的解析式有什么异同点?
(1)如果张红以1元/????????的价格购买了某种蔬菜????????????,那么她需要支付????=????元,这里????是????的函数;
(2)如果正方形的边长为????,那么正方形的面积????=????????,这里????是????的函数;
(3)如果立方体的棱长为????,那么立方体的体积????=????????,这里????是????的函数;
?
(4)如果一个正方形场地的面积为????,那么这个正方形场地的边长????=????(????也可以表示为????????????) ,这里????是????的函数;
(5)如果某人?????????内骑车行进了????????????,那么他骑车的平均速度????=????????????????/????,即????=?????????,这里????是????的函数.
?
追问2-1.上述五个例子中的函数
????=?????,????=????????,????=????????.,
?????????????????????=????即????=????????????, ????=????????,即????=?????????
在结构形式上都有什么共同特征?
?
追问2-2.每个函数中的自变量都处在函数表达式中的什么位置?指数中含有变量吗?
小结汇总讨论成果
这些函数的解析式都有幂的形式,而且都是以幂的底数为自变量;幂的指数都是常数.
追问2-3.如果将上述五个函数中的自变量统一用????表示,因变量用y表示,请你将它们分别表示出来.
?
????=?????, ????=????????,????????=????????.??????????=????????????, ????=?????????
?
追问2-4. 上述五个函数能否统一表示为????=????????(????为常数).
?
一般地,函数????=????????叫做幂函数,其中????是自变量,????是常数.
?
1.下列函数是幂函数的是(????)
A. ????=2???? B. ????=????2?1 C. ????=????3 D.????=2????
?
2.若函数????=????????+????2?5????+6是幂函数,且是奇函数,则????=(????)
A. 1 B. 2 C. 3 D. 4
?
解:根据形如????=?????????(????为常数)的函数为幂函数,故选C
?
解:因为函数是幂函数,则????2?5????+6=0,可得????=2或????=3.
又因为函数是奇函数,
当????=2时,????2为偶函数(舍);
当????=3时,????3为奇函数,符合题意.
?
3.若幂函数f(x)的图象经过点(3,33),则其定义域为 ( )
A. {????|????∈????且????>0} B. {????|????∈????且????<0}
C. {????|????∈????且????≠0} D. ????
?
解:∵????(????)为幂函数,∴设????(????)=????????
又????(????)的图像经过点(3,33),
∴33=3????,解得:????=?12,∴????(????)=?????12=1????,
∴????(????)的定义域为{????|????∈????且????>0}.
?
问题3:现在我们掌握了幂函数的解析式,接着我们继续探究幂函数的性质,我们可以用什么方法呢?
追问3-1. 前面我们用了什么方法探究“一元二次不等式的解法、函数单调性及奇偶性”呢 ?
请你在同一坐标系中画出上述五个函数图像.
问题4:我们如何画出函数????=????3和????=????12的图像呢?
?
追问4-1.可以用描点法画函数????=????3和????=????12的图像吗?
?
追问4-1.可以用描点法画函数y=x3和y=x12的图像吗?
?
追问4-2. 函数y=x3和y=x12的定义域是什么?
?
追问4-3. 函数y=x3和y=x12的奇偶性是什么?
?
追问4-4. 函数y=x3和y=x12的单调性是什么?
?
讨论成果汇总:
y=x3定义域为R,是奇函数且在R上严格单调递增
?
讨论成果汇总:
y=x3定义域为R,是奇函数且在R上严格单调递增
????=????12定义域为(0,+∞),是非奇非偶函数且在(0,+∞)上严格单调递增
?
追问4-5.你能根据y=x3和y=x12的性质画出它们的图像吗?
?
经过上述的讨论,最终得到五个函数在同一坐标系中的图像,如图所示.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????=????3
????=????????
????=????
????=????????????
????=?????????
定义域
值 域
奇偶性
单调性
问题五:观察五个函数图像,它们有哪些共同性质?
有哪些不同性质?并将它们填入下表.
(1)定点:所有的幂函数在(????,+∞)都有定义,并且图象都过点(????,????)
(2)单调性:当?????>????时,在区间[????,+∞)上是增函数
当????<????时,幂函数在区间(????,+∞)上是减函数.
(3)奇偶性:
当α为奇数时,幂函数为奇函数
当α为偶数时,幂函数为偶函数
?
(4)幂函数????=????????的图象分布与幂指数α的关系具有如下规律:在直线x=1的右侧,按“逆时针”方向,图象所对应的幂指数依次增大(如图).
?
如图,①②③④对应四个幂函数的图象,其中②对应的幂函数是.( )
????=????3 B. ????=????2
C. ????=???? D. ????=????
?
解:根据幂函数的图象以及性质以及选项得:
①是????=????,②是????=????,③是????=????2,④是????=????3.
故选:????.
?
2.下列关于幂函数的图象和性质的描述中正确的有 ( )
幂函数的图象都过点(1,1)
B. 幂函数的图象都不经过第四象限
C. 幂函数必定是奇函数或偶函数中的一种
D. 幂函数必定是增函数或减函数中的一种
解:由幂函数的图象可知????,B正确;
对于????、存在幂函数????=????是非奇非偶函数,故C错误;
对于????、存在幂函数????=????0不具有单调性,故D错误,
故选AB.
?
3.已知????????=????12, 若0
?
解:因为0又函数????(????)=????12在(0,+∞)上单调递增.
所以????(????)?
4.证明幂函数????(????)=????是增函数.
?
证明:函数的定义域是[????,+∞).
?????????,????????∈[????,+∞),且???????? ?????????????????????????=?????????????????
=(?????????????????)(????????+????????)????????+????????
=?????????????????????????+????????
∵?????????????????????,
∴????(????????)?
(1)幂函数的概念;
(2)5个常见幂函数的图象及其性质;
(3)幂函数的性质;
(4)幂函数比较大小的方法.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
