2022—2023学年人教版九年级数学上册22.1.3二次函数y=a(x-h)2+k的图象和性质(1) 课件(共19张PPT)
文档属性
| 名称 | 2022—2023学年人教版九年级数学上册22.1.3二次函数y=a(x-h)2+k的图象和性质(1) 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 469.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 20:15:22 | ||
图片预览






文档简介
(共19张PPT)
第16课时
二次函数 的图像和性质
一、学习目标
1、会画二次函数
的图象;
2、掌握二次函数
的性质.
二、新课引入
抛物线
对称轴为 ,顶点坐标为________,
它是由抛物线
个单位长度所得.
开口 ,
向 平移
向下
左
2
三、新课讲授
知识点一
认真阅读课本第35至37页的内容,完成下面
练习并体验知识点的形成过程.
的图象和性质
例3 画出函数
并指出它的开口方向、对称轴和顶点.
的图象,
描点并连线:
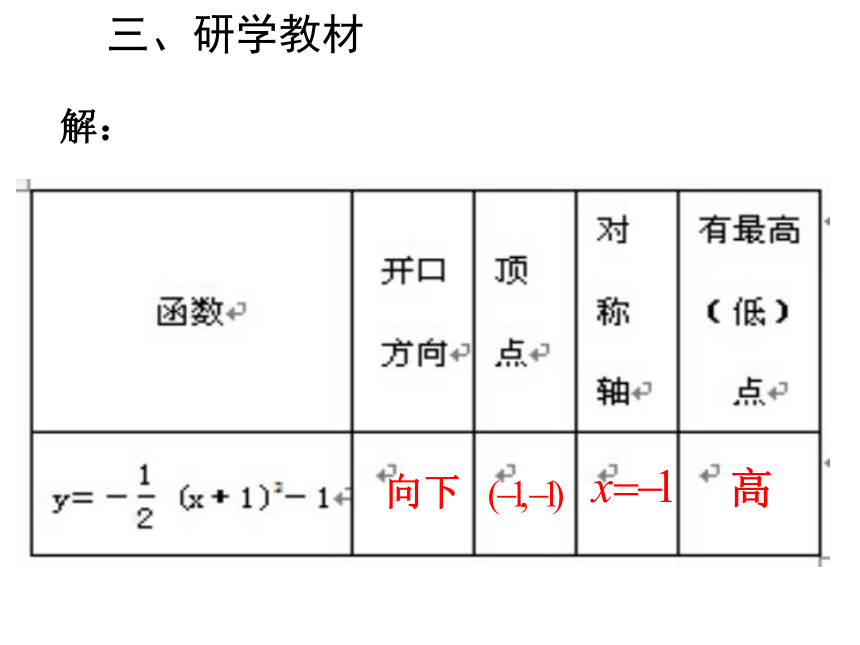
三、研学教材
解:
三、研学教材
向下
高
1、怎样移动抛物线
就可以得到抛物线
?
解:把抛物线
再向_____平移_____个单位,就得到抛物线
向____平移____个单位,
.
三、研学教材
下
1
左
1
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线
?
2、细想一下,你还有其他的平移方法吗?
三、研学教材
解:把抛物线
再向_____平移_____个单位,就得到抛物线
向____平移____个单位,
.
左
1
下
1
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线 ?
把抛物线
再向右平移1个单位,那么所得抛物线
是___ __.
先向上平移2个单位,
练一练
三、研学教材
归纳 一般地,抛物线
与
形状_______,位置______.
把抛物线
向上(下)向左(右)
.平移的方向、距离要根据_____、____的
值来决定.
向上(下)向左(右)
三、研学教材
相同
不同
抛物线
有如下特点:
当 时,开口向____,且若当 时,
随 的增大而_____,若 时, 随
的增大而______;
当 时,开口向____,且若当 时,
随 的增大而______,若 时, 随
的增大而______ .
(1)
h
x
>
(2)对称轴是 ________;
(3)顶点是( , ).
三、研学教材
上
减小
增大
下
增大
减小
练一练
说出下列抛物线的开口方向、对称轴和顶点.
三、研学教材
开口向上,对称轴为: ,顶点为:
开口向下,对称轴为: ,顶点为:
开口向上,对称轴为: ,顶点为:
开口向下,对称轴为: ,顶点为:
拓展提升
根据条件求二次函数的解析式
抛物线的顶点坐标为(-1,-1),且与y轴交点的纵坐标为-3.
四、归纳小结
1、可以通过描点法或 画出二次函
数 的图象.
2、抛物线 中, 决定抛物线的形状, , 决定抛物线的位置.
平移法
一填空题
抛物线 可由抛物线 向___平移___ 个单位长度得到.
左
1
堂清
二.
抛物线 向右平移1个单位,再向下平移2个单位,所得到的抛物线是----
堂清
我相信,只要大家勤于思考,勇于探索,一定会获得很多的发现,增长更多的见识,谢谢大家,再见!
第16课时
二次函数 的图像和性质
一、学习目标
1、会画二次函数
的图象;
2、掌握二次函数
的性质.
二、新课引入
抛物线
对称轴为 ,顶点坐标为________,
它是由抛物线
个单位长度所得.
开口 ,
向 平移
向下
左
2
三、新课讲授
知识点一
认真阅读课本第35至37页的内容,完成下面
练习并体验知识点的形成过程.
的图象和性质
例3 画出函数
并指出它的开口方向、对称轴和顶点.
的图象,
描点并连线:
三、研学教材
解:
三、研学教材
向下
高
1、怎样移动抛物线
就可以得到抛物线
?
解:把抛物线
再向_____平移_____个单位,就得到抛物线
向____平移____个单位,
.
三、研学教材
下
1
左
1
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线
?
2、细想一下,你还有其他的平移方法吗?
三、研学教材
解:把抛物线
再向_____平移_____个单位,就得到抛物线
向____平移____个单位,
.
左
1
下
1
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线 ?
把抛物线
再向右平移1个单位,那么所得抛物线
是___ __.
先向上平移2个单位,
练一练
三、研学教材
归纳 一般地,抛物线
与
形状_______,位置______.
把抛物线
向上(下)向左(右)
.平移的方向、距离要根据_____、____的
值来决定.
向上(下)向左(右)
三、研学教材
相同
不同
抛物线
有如下特点:
当 时,开口向____,且若当 时,
随 的增大而_____,若 时, 随
的增大而______;
当 时,开口向____,且若当 时,
随 的增大而______,若 时, 随
的增大而______ .
(1)
h
x
>
(2)对称轴是 ________;
(3)顶点是( , ).
三、研学教材
上
减小
增大
下
增大
减小
练一练
说出下列抛物线的开口方向、对称轴和顶点.
三、研学教材
开口向上,对称轴为: ,顶点为:
开口向下,对称轴为: ,顶点为:
开口向上,对称轴为: ,顶点为:
开口向下,对称轴为: ,顶点为:
拓展提升
根据条件求二次函数的解析式
抛物线的顶点坐标为(-1,-1),且与y轴交点的纵坐标为-3.
四、归纳小结
1、可以通过描点法或 画出二次函
数 的图象.
2、抛物线 中, 决定抛物线的形状, , 决定抛物线的位置.
平移法
一填空题
抛物线 可由抛物线 向___平移___ 个单位长度得到.
左
1
堂清
二.
抛物线 向右平移1个单位,再向下平移2个单位,所得到的抛物线是----
堂清
我相信,只要大家勤于思考,勇于探索,一定会获得很多的发现,增长更多的见识,谢谢大家,再见!
同课章节目录
