人教版选修一1.5 弹性碰撞和非弹性碰撞 课件(27张PPT)
文档属性
| 名称 | 人教版选修一1.5 弹性碰撞和非弹性碰撞 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
第一章 动量守恒定律
5 弹性碰撞和非弹性碰撞
学习目标
1.知道什么是弹性碰撞、非弹性碰撞和完全非弹性碰撞,正碰(对心碰撞)和斜碰(非对心碰撞)
2.会用动量、能量的观点综合分析、解决一维碰撞问题。
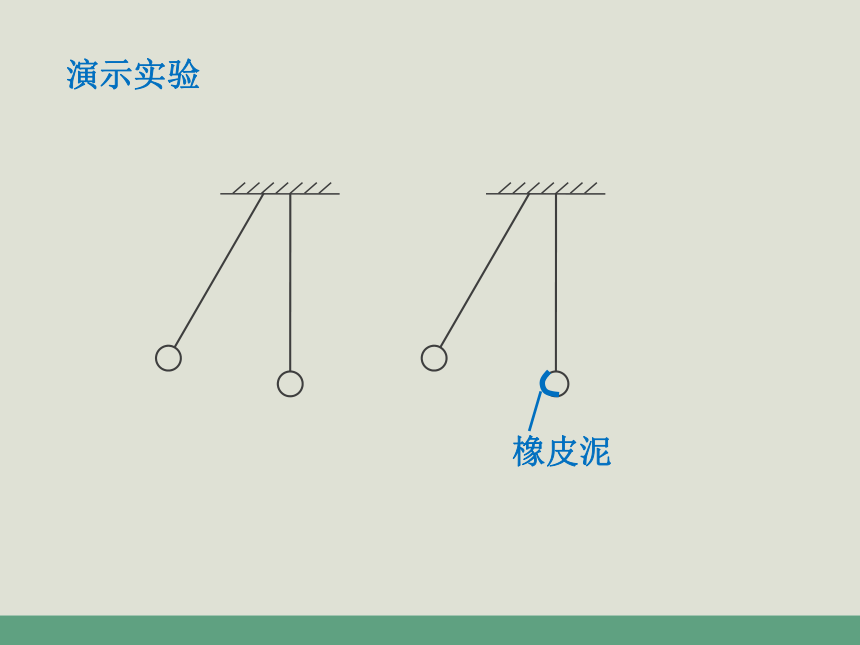
橡皮泥
演示实验
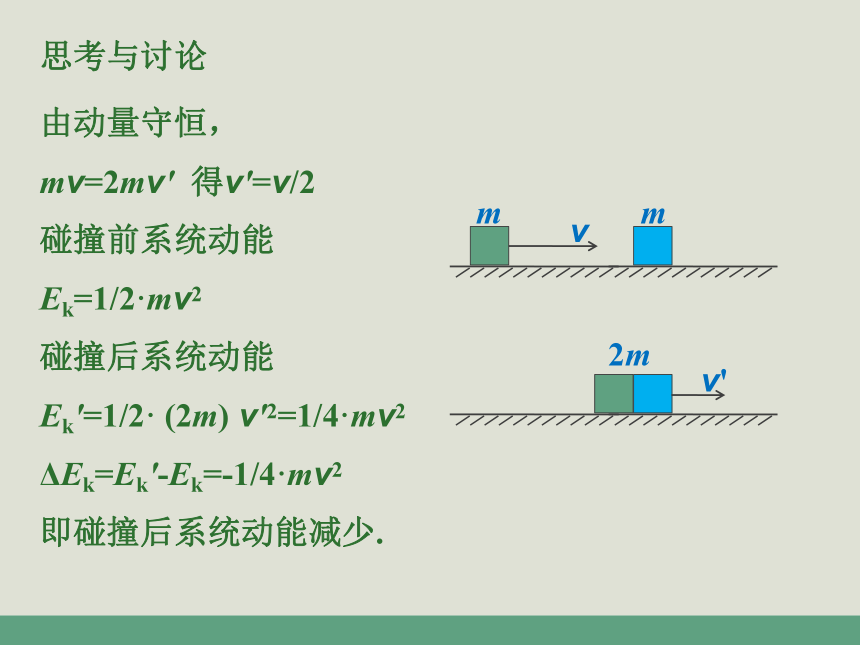
思考与讨论
由动量守恒,
mv=2mv' 得v'=v/2
碰撞前系统动能
Ek=1/2·mv2
碰撞后系统动能
Ek'=1/2· (2m) v'2=1/4·mv2
ΔEk=Ek'-Ek=-1/4·mv2
即碰撞后系统动能减少.
m
m
v
v'
2m
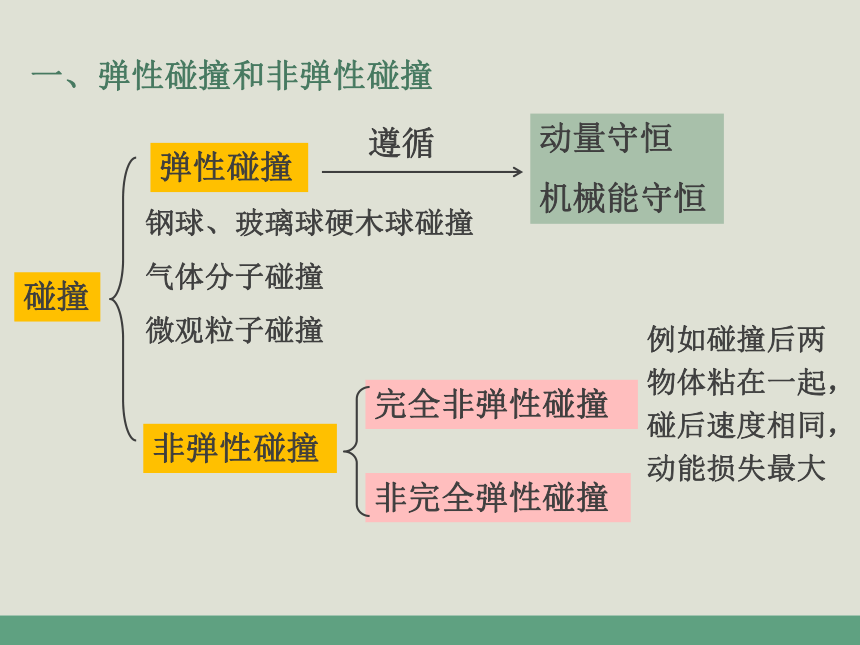
一、弹性碰撞和非弹性碰撞
钢球、玻璃球硬木球碰撞
气体分子碰撞
微观粒子碰撞
例如碰撞后两物体粘在一起,碰后速度相同,动能损失最大
碰撞
弹性碰撞
非弹性碰撞
完全非弹性碰撞
非完全弹性碰撞
动量守恒
机械能守恒
遵循
碰撞特点
在碰撞过程中,普通力(例如重力、摩擦力等有限值得力)相对于碰撞时的冲力可以忽略不计.
碰撞过程中,物体的位移可以忽略不计.
理由如下:设Δr和v为碰撞时的位移和平均速度,那么Δr=vΔt。由于v为有限值,Δt极小,因此位移大小可以忽略,认为在碰撞中物体位置来不及发生变化.
1.弹性碰撞
系统动量守恒,有
m1v1=m1v1'+m2v2'
机械能守恒,有
1/2·m1v12=1/2·m1v1'2+1/2·m2v2'2
解得
m1
m2
v1
m2
m1
v2'
v1'
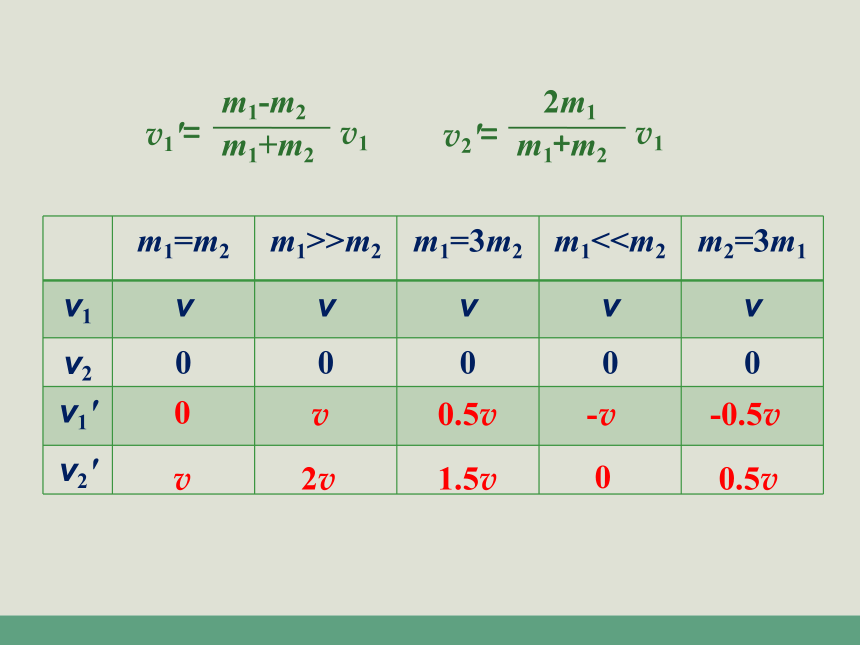
m1-m2
m1+m2
v1
v1'=
2m1
m1+m2
v1
v2'=
m1=m2 m1>>m2 m1=3m2 m1<v1 v v v v v
v2 0 0 0 0 0
v1'
v2'
0
v
v
2v
-v
0
-0.5v
0.5v
0.5v
1.5v
m1-m2
m1+m2
v1
v1'=
2m1
m1+m2
v1
v2'=
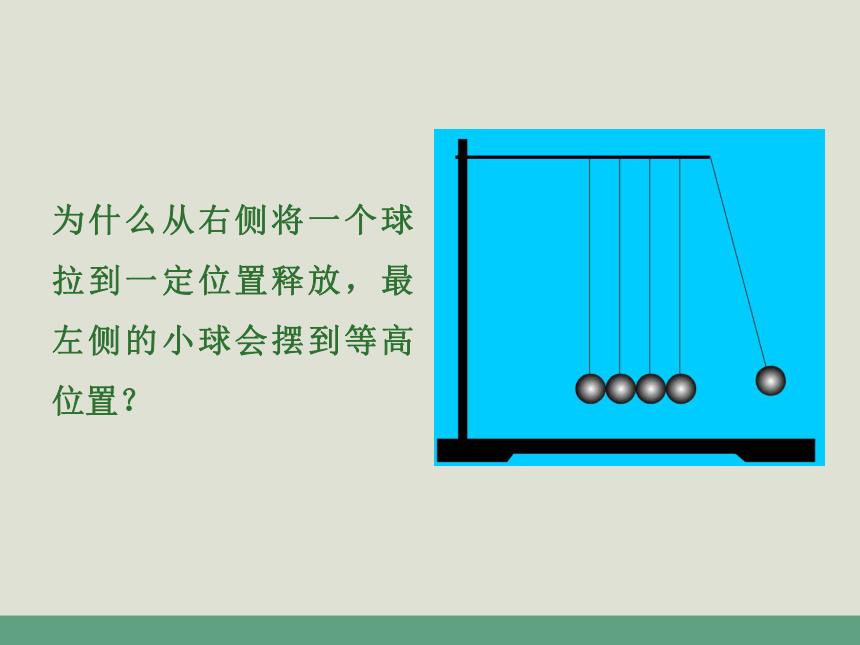
为什么从右侧将一个球拉到一定位置释放,最左侧的小球会摆到等高位置?
2.完全非弹性碰撞
系统动量守恒
m1v1+m2v2=(m1+m2) v
碰撞后速度
m2
m1
v
m1
m2
v1
v2
m1v1+m2v2
m1+m2
v=
例 1.冲击摆
冲击摆可用于测量子弹速率。长度为l 的线绳悬挂质量为m的木块,子弹质量为m0,沿水平方向射入木块,子弹最后嵌在木块内一定位置,且测得木块摆过的角度为θ,m>>m0,求子弹射入的速率v0.
θ
m
m0
第一阶段:子弹和木块开始接触直至达到共同速度。子弹和木块发生完全非弹性碰撞,获得共同速度时,木块向右有微小偏离,绳的拉力在水平方向有分力,水平方向外力和不为零。因子弹和木块相互作用内力很大,木块向右偏离很小,故绳拉力的水平分量远小于内力,可用沿水平方向动量守恒求近似解。可认为子弹和木块达到共同速度时,木块仍然在原位置。
θ
m
m0
第二阶段:子弹和木块作为一个整体摆到最高点。
视木块、子弹为一个质点,认为悬线竖直瞬间二者已经获得共同速度。摆动过程中机械能守恒,可求出共同速度。
θ
m
m0
解:设子弹和木块的共同速度为v,
由动量守恒:m0v0=(m+m0)v ①
摆到最高点,机械能守恒
1/2·(m+m0)v2=(m+m0)g(l-lcosθ) ②
解①②得
m+m0
m0
v0=
√
2gl(1-cosθ)
二、对心碰撞和非对心碰撞
对心碰撞(正碰)
两球碰撞前的速度矢量都沿着两球的连心线,碰撞后的速度也必然沿着两球连心线的方向
非对心碰撞(斜碰)
两球相碰之前的速度不沿它们的中心连线,这种碰撞叫作球的非对心碰撞或者斜碰.
B
A
B
A
B
A
B
A
思考与讨论如图所示,A球以速度v1与同样质量且处于静止的B球碰撞。已知碰撞后B球的速度如图所示,请大致画出碰撞后A球的速度.BAv1BAv2解:由动量守恒mv1=mv1'+mv2',即v1=v1'+v2',因此三个速度构成封闭三角形。v1'若为弹性碰撞,则动能不变
v1'
v1
v2'
上式说明速度三角形是以v1为斜边的直角三角形,速度v1'与v2'垂直,即碰撞后,A、B球的运动方向互相垂直。
α粒子(氦原子核)与氦原子碰撞,碰撞后速度彼此垂直
(α粒子从图中左侧入射)
小结
1.知道弹性碰撞和非弹性碰撞的含义
2.理解弹性碰撞的规律:动量守恒和机械能守恒;能3.够推导弹性碰撞后物体的速度表达式
4.对心碰撞和非对心碰撞的含义;了解非对心碰撞的处理方法
拓展Ⅰ:一般弹性正碰
m2
m1
v2'
v1'
m1
m2
v1
v2
m1m2v1v2m1m2v1-v2碰撞后相对于地面的速度为拓展Ⅱ :恢复系数e
恢复系数e定义为
实验发现,恢复系数由两球材料的弹性决定,可利用气垫导轨进行测量.
e=1,弹性碰撞
e=0,完全非弹性碰撞
01.证明e=1为弹性碰撞
e=1,v1-v2=v2'-v1',移项v1+v1'=v2'+v2①
动量守恒 m1v1+m2v2=m1v1'+m2v2',
移项, m1 (v1-v'1) =m2(v2'-v2) ②
①②式左边和右边相乘得:m1 (v12-v1'2) =m2(v2'2-v22)
移项,同时乘以1/2,得到
2.e=0为完全非弹性碰撞
若e=0,则v2'=v1',碰撞后两物体速度相同,两物体粘在一起成为一个整体,即完全非弹性碰撞。
3.碰撞时的能量损失
由动量守恒 m1 v1 = m1 v1'+m2 v2'
恢复系数e =(v2'-v1')/v1
解得
m1
m2
v1
m2
m1
v2'
v1'
1. e=1,无能量损失,为弹性碰撞
2. e=0,有能量损失,且能量损失最大,为完全非弹性碰撞
3. 0看
观
谢
谢
第一章 动量守恒定律
5 弹性碰撞和非弹性碰撞
学习目标
1.知道什么是弹性碰撞、非弹性碰撞和完全非弹性碰撞,正碰(对心碰撞)和斜碰(非对心碰撞)
2.会用动量、能量的观点综合分析、解决一维碰撞问题。
橡皮泥
演示实验
思考与讨论
由动量守恒,
mv=2mv' 得v'=v/2
碰撞前系统动能
Ek=1/2·mv2
碰撞后系统动能
Ek'=1/2· (2m) v'2=1/4·mv2
ΔEk=Ek'-Ek=-1/4·mv2
即碰撞后系统动能减少.
m
m
v
v'
2m
一、弹性碰撞和非弹性碰撞
钢球、玻璃球硬木球碰撞
气体分子碰撞
微观粒子碰撞
例如碰撞后两物体粘在一起,碰后速度相同,动能损失最大
碰撞
弹性碰撞
非弹性碰撞
完全非弹性碰撞
非完全弹性碰撞
动量守恒
机械能守恒
遵循
碰撞特点
在碰撞过程中,普通力(例如重力、摩擦力等有限值得力)相对于碰撞时的冲力可以忽略不计.
碰撞过程中,物体的位移可以忽略不计.
理由如下:设Δr和v为碰撞时的位移和平均速度,那么Δr=vΔt。由于v为有限值,Δt极小,因此位移大小可以忽略,认为在碰撞中物体位置来不及发生变化.
1.弹性碰撞
系统动量守恒,有
m1v1=m1v1'+m2v2'
机械能守恒,有
1/2·m1v12=1/2·m1v1'2+1/2·m2v2'2
解得
m1
m2
v1
m2
m1
v2'
v1'
m1-m2
m1+m2
v1
v1'=
2m1
m1+m2
v1
v2'=
m1=m2 m1>>m2 m1=3m2 m1<
v2 0 0 0 0 0
v1'
v2'
0
v
v
2v
-v
0
-0.5v
0.5v
0.5v
1.5v
m1-m2
m1+m2
v1
v1'=
2m1
m1+m2
v1
v2'=
为什么从右侧将一个球拉到一定位置释放,最左侧的小球会摆到等高位置?
2.完全非弹性碰撞
系统动量守恒
m1v1+m2v2=(m1+m2) v
碰撞后速度
m2
m1
v
m1
m2
v1
v2
m1v1+m2v2
m1+m2
v=
例 1.冲击摆
冲击摆可用于测量子弹速率。长度为l 的线绳悬挂质量为m的木块,子弹质量为m0,沿水平方向射入木块,子弹最后嵌在木块内一定位置,且测得木块摆过的角度为θ,m>>m0,求子弹射入的速率v0.
θ
m
m0
第一阶段:子弹和木块开始接触直至达到共同速度。子弹和木块发生完全非弹性碰撞,获得共同速度时,木块向右有微小偏离,绳的拉力在水平方向有分力,水平方向外力和不为零。因子弹和木块相互作用内力很大,木块向右偏离很小,故绳拉力的水平分量远小于内力,可用沿水平方向动量守恒求近似解。可认为子弹和木块达到共同速度时,木块仍然在原位置。
θ
m
m0
第二阶段:子弹和木块作为一个整体摆到最高点。
视木块、子弹为一个质点,认为悬线竖直瞬间二者已经获得共同速度。摆动过程中机械能守恒,可求出共同速度。
θ
m
m0
解:设子弹和木块的共同速度为v,
由动量守恒:m0v0=(m+m0)v ①
摆到最高点,机械能守恒
1/2·(m+m0)v2=(m+m0)g(l-lcosθ) ②
解①②得
m+m0
m0
v0=
√
2gl(1-cosθ)
二、对心碰撞和非对心碰撞
对心碰撞(正碰)
两球碰撞前的速度矢量都沿着两球的连心线,碰撞后的速度也必然沿着两球连心线的方向
非对心碰撞(斜碰)
两球相碰之前的速度不沿它们的中心连线,这种碰撞叫作球的非对心碰撞或者斜碰.
B
A
B
A
B
A
B
A
思考与讨论如图所示,A球以速度v1与同样质量且处于静止的B球碰撞。已知碰撞后B球的速度如图所示,请大致画出碰撞后A球的速度.BAv1BAv2解:由动量守恒mv1=mv1'+mv2',即v1=v1'+v2',因此三个速度构成封闭三角形。v1'若为弹性碰撞,则动能不变
v1'
v1
v2'
上式说明速度三角形是以v1为斜边的直角三角形,速度v1'与v2'垂直,即碰撞后,A、B球的运动方向互相垂直。
α粒子(氦原子核)与氦原子碰撞,碰撞后速度彼此垂直
(α粒子从图中左侧入射)
小结
1.知道弹性碰撞和非弹性碰撞的含义
2.理解弹性碰撞的规律:动量守恒和机械能守恒;能3.够推导弹性碰撞后物体的速度表达式
4.对心碰撞和非对心碰撞的含义;了解非对心碰撞的处理方法
拓展Ⅰ:一般弹性正碰
m2
m1
v2'
v1'
m1
m2
v1
v2
m1m2v1v2m1m2v1-v2碰撞后相对于地面的速度为拓展Ⅱ :恢复系数e
恢复系数e定义为
实验发现,恢复系数由两球材料的弹性决定,可利用气垫导轨进行测量.
e=1,弹性碰撞
e=0,完全非弹性碰撞
0
e=1,v1-v2=v2'-v1',移项v1+v1'=v2'+v2①
动量守恒 m1v1+m2v2=m1v1'+m2v2',
移项, m1 (v1-v'1) =m2(v2'-v2) ②
①②式左边和右边相乘得:m1 (v12-v1'2) =m2(v2'2-v22)
移项,同时乘以1/2,得到
2.e=0为完全非弹性碰撞
若e=0,则v2'=v1',碰撞后两物体速度相同,两物体粘在一起成为一个整体,即完全非弹性碰撞。
3.碰撞时的能量损失
由动量守恒 m1 v1 = m1 v1'+m2 v2'
恢复系数e =(v2'-v1')/v1
解得
m1
m2
v1
m2
m1
v2'
v1'
1. e=1,无能量损失,为弹性碰撞
2. e=0,有能量损失,且能量损失最大,为完全非弹性碰撞
3. 0
观
谢
谢
