2013年秋初一数学期末复习教学案
图片预览


文档简介
2013年秋初一数学期末复习教学案(一)
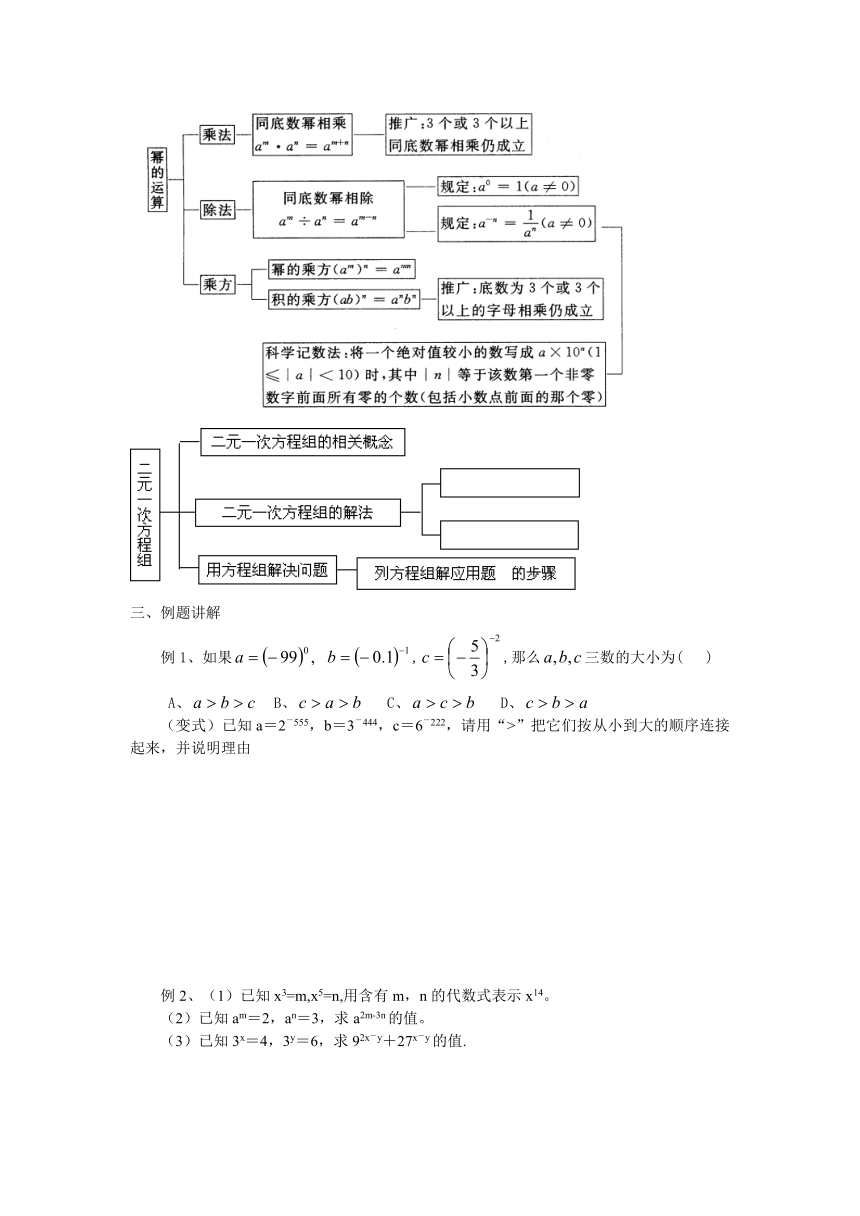
幂的运算及二元一次方程组(应用)复习
编写: 班级_____ 姓名_______
一、基础训练
1、102·107 = ,(m4)3= ,(2a)4= ;a5÷(-a2 )·a=_____
2、 (-a)3·(-a)= ,(-b2)3= , (-3xy)2=
3、方程的自然数解有 组,分别为
4、下列各式(1) (2) (-2a)= (3) ()= (4) ,其中计算错误的有( )
A、1个 B、2个 C、3个 D、4个
5、如果 ,,那么三数的大小为( )
A、 B、 C、 D、
6、若xa-b-2ya+b-2=11是二元一次方程,那么的a、b值分别是( )
A、1,0 B、0,-1 C、2,1 D、2,-3
7、若方程组的解满足=0,则的取值是( )
A、=-1 B、=1 C、=0 D、不能确定
8、某校办工厂去年总利润(总利润=总收入-总支出)为50万元。计划今年的总收入比去年增加10%,总支出节约20%,这样今年总利润为58万元,若设去年总支出为x万元,总收入为y万元。则根据题意,可得方程组为:______
二、要点梳理
三、例题讲解
例1、如果 ,,那么三数的大小为( )
A、 B、 C、 D、
(变式)已知a=2-555,b=3-444,c=6-222,请用“>”把它们按从小到大的顺序连接起来,并说明理由
例2、(1)已知x3=m,x5=n,用含有m,n的代数式表示x14。
(2)已知am=2,an=3,求a2m-3n的值。
(3)已知3x=4,3y=6,求92x-y+27x-y的值.
例3、对于有理数x,y定义一种运算“△”:x△y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算,已知3△5=15,4△7=28,求1△1的值。
例4、进入讯期,七年级1班的同学们到水库去调查了解汛情,水库一共10个泻洪闸,现在水库水位超过安全线,上游的河水仍以一个不变的速度流入水库。同学们经过一天的观察和测量,做如下的记录:上午打开1个泻洪闸,在2小时内,水位继续上涨了0.66m。下午再打开2个泻洪闸后,4小时水位下降了0.1m,目前水位仍超过安全线1.2m。
(1)如果打开了5个泻洪闸,还需几小时水位可以降到安全线?
(2)如果防讯指挥部要求在6小时内水位降到安全线,应该打开几个泻洪闸?
例5、在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆”;
乙同学说:“四环路比三环路车流量每小时多2000辆”;
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”;
请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
四、强化训练
1、已知a≠0,b≠0,有以下五个算式: ①am·a-m÷bn=b-n;②am÷bm=;③(a2b3)m=(am)2·(bm)2;④(a+b)m+1-a·(a+b)m=b(a+b)m;
⑤(am+bn)2=a2m+b2n,其中正确的有( )
A、2个 B、4个 C、3个 D、5个
2、=_____,(xn)2+5xn-2·xn+2=______
3、3-2+(-3)2+(π-3.14)0=___,用科学记数法表示0.0000168=___
4、已知2a·27b·37c=1998,其中a、b、c是自然数,求(a-b-c)-2014.
5、某种花粉颗粒的半径约为25 um,多少个这样的花粉颗粒顺次排列能达到1m.其中1um=10-6m.(结果用科学记数法表示)
6、小明用8个一样大的矩形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的矩形;图案甲的中间留下了边长是2cm的正方形小洞.求(a+2b)2-8ab的值.
7、七(13)、七(14)两班学生到集市上购买苹果,苹果的价格如右表:
七(14)班分两次共购买苹果70千克(第二次多于第一次),共付出189元,而七(13)班则一次购苹果70千克。
购买苹果数
不超过30千克
30千克以上但不超过50千克
50千克以上
每千克价格
3元
2.5元
2元
(1)七(13)班比甲七(14)班少付多少元?
(2)七(14)班第一次、第二次分别购买苹果多少千克?
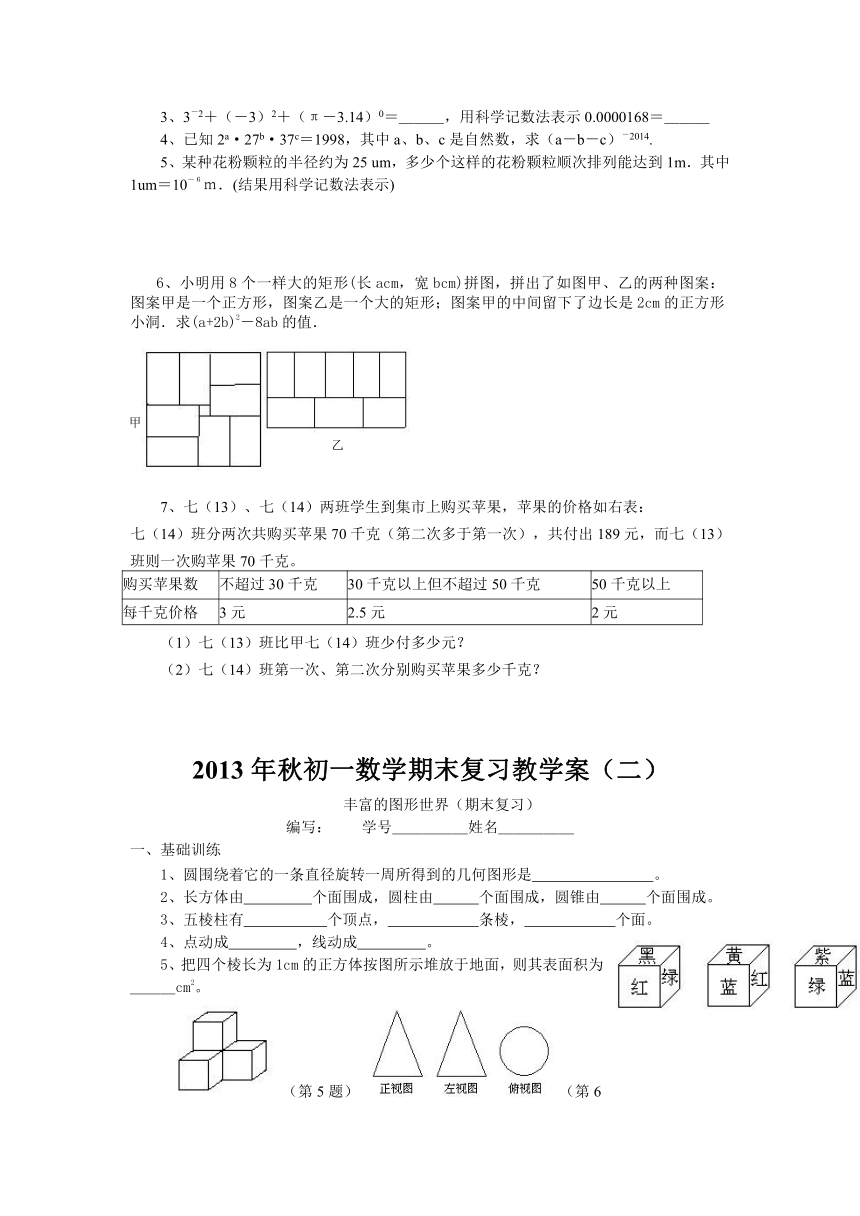
2013年秋初一数学期末复习教学案(二)
丰富的图形世界(期末复习)
编写: 学号_____姓名_____
一、基础训练
1、圆围绕着它的一条直径旋转一周所得到的几何图形是 。
2、长方体由 个面围成,圆柱由 个面围成,圆锥由 个面围成。
3、五棱柱有 个顶点, 条棱, 个面。
4、点动成 ,线动成 。
5、把四个棱长为1cm的正方体按图所示堆放于地面,则其表面积为___cm2。
(第5题)(第6题)
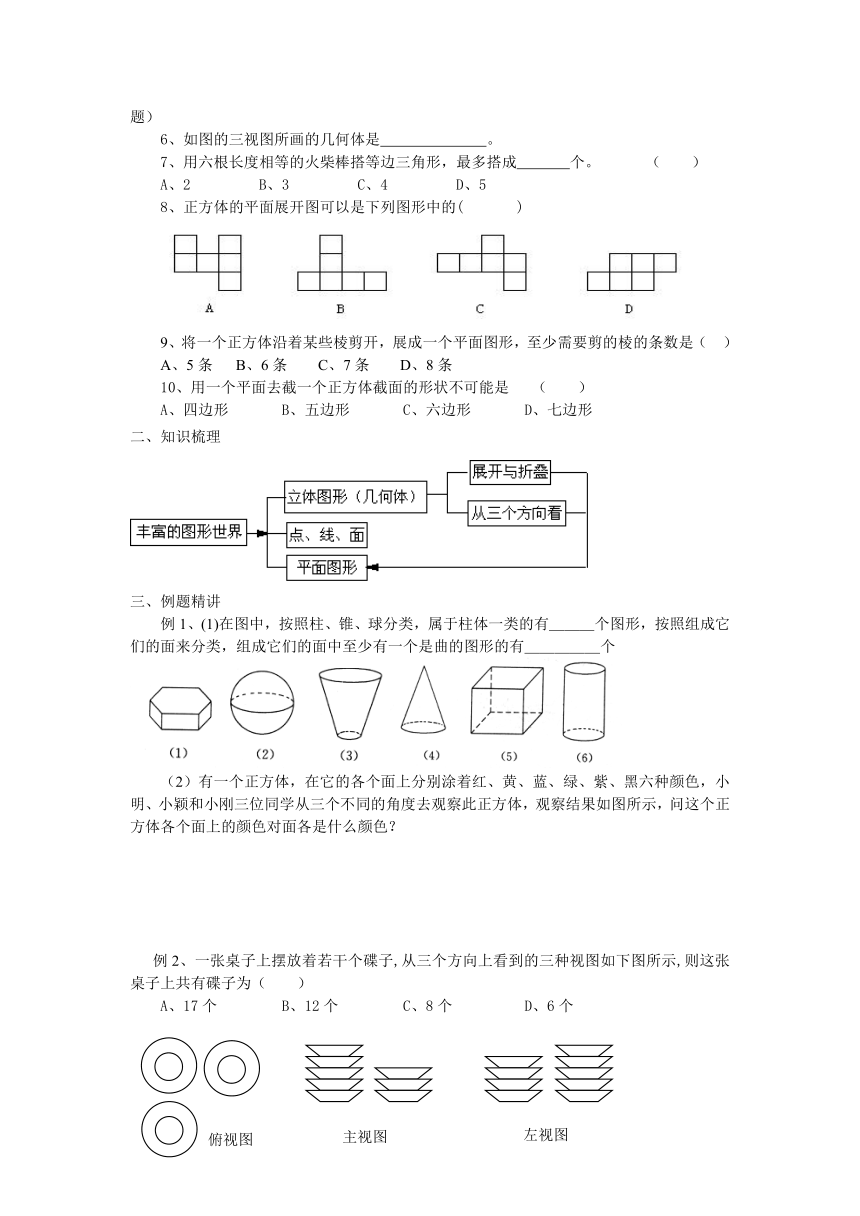
6、如图的三视图所画的几何体是 。
7、用六根长度相等的火柴棒搭等边三角形,最多搭成 个。 ( )
A、2 B、3 C、4 D、5
8、正方体的平面展开图可以是下列图形中的( )
9、将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是( )
A、5条 B、6条 C、7条 D、8条
10、用一个平面去截一个正方体截面的形状不可能是 ( )
A、四边形 B、五边形 C、六边形 D、七边形
二、知识梳理
三、例题精讲
例1、(1)在图中,按照柱、锥、球分类,属于柱体一类的有___个图形,按照组成它们的面来分类,组成它们的面中至少有一个是曲的图形的有_____个
(2)有一个正方体,在它的各个面上分别涂着红、黄、蓝、绿、紫、黑六种颜色,小明、小颖和小刚三位同学从三个不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的颜色对面各是什么颜色?
例2、一张桌子上摆放着若干个碟子,从三个方向上看到的三种视图如下图所示,则这张桌子上共有碟子为( )
A、17个 B、12个 C、8个 D、6个
例3、(1)在建筑工地上,一垛垛的红砖整齐地码放着,如图所示,是几个红砖排成的几何体的俯视图,图中的数字表示的是该位置摆放的红砖的层次数,请你画出它的正视图和左视图.
2
3
2
2
2
2
1
1
1
(2)如右图,是由一些棱长都为1cm的小正方体组合
成的简单几何体.
①该几何体的表面积(含下底面)为 ;
②该几何体的主视图如图所示,请在下面方格纸中分别画
出它的左视图和俯视图.
例4、如图是用积木摆放的一组图案,观察图形并探索:第五个图案中共有____块积木,第n个图案中共有____块积木.
例5、在如图所示的12×13的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移6格后的△A1B1C1,再画出△ABC以点C为旋转中心,顺时针方向旋转90°后的△A2B2C2.
(2)在与同学交流时,你打算如何描述①中所画的△A2B2C2的位置?
四、强化训练
1、如图是一个正方体的展开图,如果正方体相对的面上标注的值相等,那么x=_____,y=_____
(第2题) (第3题)
2、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,图是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面,则“祝”、“你”、“前”分别表示正方体的___________
3、如图所示的几何体的右视图是( )
4、由一些大小相同的小正方体组成的简单几何体的正视图和俯视图,如图所示.
(1)请你画出这个几何的左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
5、一个正方体的平面展开图如图所示,如果将它恢复成原来的正方体,那么点E和点___重合,点J和点___重合.
6、若由相同的小正方体构成的立体图形的三视图如图所示:
那么,这个立体图形最少是由_____个小正方体构成的.
7、由几个小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体的主视图和左视图.
2013年秋初一数学期末复习教学案(三)
平面图形的认识(一)
编写:学号_____姓名_____
一、基础训练
1、下列说法错误的是( )
A、两点确定一条直线 B、过一点可以画无数条直线
C、过已知三点可能画一条直线 D、平角是直线
2、下列说法中正确的是( )
A、延长直线AB B、延长射线OA
C、反向延长射线OA到P,使OP=OA D、延长线段AB到C,使AB=BC
3、如图,可以用字母表示出来的不同的线段和射线的条数分别是( )
A、3和3 B、3和4
C、6和3 D、3和1
4、如果∠1和∠2是邻补角,且∠1>∠2,那么∠2的余角是( )
A、(∠1-∠2) B、∠1 C、(∠1+∠2) D、∠2
5、下列图中,∠1与∠2是对顶角的是( )
6、如果∠α等于它的余角的2倍,则∠α的补角等于_____
7、如图,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=28°,则∠EOF=_____°
8、8点30分时,时钟的时针与分针所夹的锐角是( )
A、70° B、75° C、80° D、60°
9、(1)23°30′=________°;(2)78.36°= ______°____′________″。
10、如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
(1)若∠AOC=∠AOB,则OC的方向是_______:
(2)OD是OB的反向延长线,OD的方向是_______.
二、例题讲解
例1、已知线段AB=48cm,C是线段AB的中点,D是CB的中点,点E在AB上,且CE=AC,画图并求线段DE的长.
例2、直线AB、CD交于O,OE平分∠AOC,∠COF=90°,∠BOF=42°,
求∠COE的度数。
例3、(1) 如图l所示,将书页折过去,使角顶点 A落在A′处,BC为折痕,BD
为∠A′BE的平分线,求∠CBD的度数.
(2)如图2,要用一张长方形纸折成一个纸袋,两条折痕的夹角为70°(即∠POQ=70°),将折过来的重叠部分抹上胶水,即可做成一个纸袋,则粘胶水部分所构成的∠A'OB'=______.
(图1)(图2)
例4、如图,在方格纸上有一条线段AB和一点C. ①过点C画出与AB平行的直线;
②过点C画出与AB垂直的直线.
例5、已知:如图, OA⊥OB,∠AOC=460,OM平分∠AOC,ON平 分∠BOC,则∠MON的度数为 ;
变式:(1)当00<∠AOC< 900时,∠MON的度数是 ;
(2)当900<∠AOC<1800时,∠MON的度数是 .
例6、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD。
(1)图中∠AOF的补角是 (把符合条件的角都填出来)。
(2)图中除直角相等外,还有相等的角,请写出所有相等的角:
(3)①如果∠AOD=130°.那么根据 ,
可得∠BOC= 度。
②如果,求∠EOF的度数。
例7、如图,已知∠AOB,画射线OC⊥OA,OD⊥OB.
(1)画出符合要求的图形;
(2)若∠AOB=30°,其他条件不变,则∠COD=_______;
(3)若(2)中∠AOB=m°,其他条件不变,则∠COD=_______;
(4)结合(1)中画图和(2)、(3)的结果,你能从中看出什么规律(用一句话来归纳)?
三、强化训练
1、对于直线AB、线段CD、射线EF,在下列各图中能相交的是( )
2、下列语句中,正确的是( )
A、射线AB与射线BA表示同一条射线
B、在同一平面内,经过一点有且只有一条直线与已知直线平行
C、在同一平面内,经过一点有且只有一条直线与已知直线垂直
D、直线l1∥l2,l2∥l3,则l1∥l3,理由是等量代换
3、小孩子玩玩具手枪,在瞄准时总是半闭着眼,对着准星与目标,用数学知识解释为_______.
4、下列说法:①两点之间的距离是两点间的线段;②如果两条线段没有交点,那么这两条线段所在直线也没有交点;③邻补角的两条角平分线构成一个直角;④同一平面内,过一点有且只有一条直线与已知直线垂直;⑤同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( )
A、1个 B、2个 C、3个 D、4个
5、已知∠AOB=50°,以OB为一边画∠BOC=20°,则∠AOC=____°
6、已知线段AB=20cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,则AM=_____cm
7、如图是一个马路上的人行横道线,即斑马线的示意图,请你根据图示判断在过马路时三条线路AC、AB、AD中最短的是_______.
第7题 第8题
8、如图,要把角钢①变成120°的角钢②,则角钢①上截去的缺口的度数是_______.
9、我们知道:式子|x-3|的几何意义是数轴上表示数x的点与表示数3的点之间的距离,则式子|x-2|+|x+1|的最小值是为_____
10、(1)如图1,在方格纸中有三个格点三角形(顶点在小正方形的顶点上),把三角形ABC绕点A顺时针旋转90°,可以得到三角形ADE,再将三角形ADE向左平移5格,得到三角形FHG,图中,直线AB、AD、FH两两之间有怎样的位置关系?
(2)如图2,用直尺过点A画AD⊥AB,过点C画CF⊥AB,垂足为F,并在图中标出直线AD、CF经过的格点.
幂的运算及二元一次方程组(应用)复习
编写: 班级_____ 姓名_______
一、基础训练
1、102·107 = ,(m4)3= ,(2a)4= ;a5÷(-a2 )·a=_____
2、 (-a)3·(-a)= ,(-b2)3= , (-3xy)2=
3、方程的自然数解有 组,分别为
4、下列各式(1) (2) (-2a)= (3) ()= (4) ,其中计算错误的有( )
A、1个 B、2个 C、3个 D、4个
5、如果 ,,那么三数的大小为( )
A、 B、 C、 D、
6、若xa-b-2ya+b-2=11是二元一次方程,那么的a、b值分别是( )
A、1,0 B、0,-1 C、2,1 D、2,-3
7、若方程组的解满足=0,则的取值是( )
A、=-1 B、=1 C、=0 D、不能确定
8、某校办工厂去年总利润(总利润=总收入-总支出)为50万元。计划今年的总收入比去年增加10%,总支出节约20%,这样今年总利润为58万元,若设去年总支出为x万元,总收入为y万元。则根据题意,可得方程组为:______
二、要点梳理
三、例题讲解
例1、如果 ,,那么三数的大小为( )
A、 B、 C、 D、
(变式)已知a=2-555,b=3-444,c=6-222,请用“>”把它们按从小到大的顺序连接起来,并说明理由
例2、(1)已知x3=m,x5=n,用含有m,n的代数式表示x14。
(2)已知am=2,an=3,求a2m-3n的值。
(3)已知3x=4,3y=6,求92x-y+27x-y的值.
例3、对于有理数x,y定义一种运算“△”:x△y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算,已知3△5=15,4△7=28,求1△1的值。
例4、进入讯期,七年级1班的同学们到水库去调查了解汛情,水库一共10个泻洪闸,现在水库水位超过安全线,上游的河水仍以一个不变的速度流入水库。同学们经过一天的观察和测量,做如下的记录:上午打开1个泻洪闸,在2小时内,水位继续上涨了0.66m。下午再打开2个泻洪闸后,4小时水位下降了0.1m,目前水位仍超过安全线1.2m。
(1)如果打开了5个泻洪闸,还需几小时水位可以降到安全线?
(2)如果防讯指挥部要求在6小时内水位降到安全线,应该打开几个泻洪闸?
例5、在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆”;
乙同学说:“四环路比三环路车流量每小时多2000辆”;
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”;
请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
四、强化训练
1、已知a≠0,b≠0,有以下五个算式: ①am·a-m÷bn=b-n;②am÷bm=;③(a2b3)m=(am)2·(bm)2;④(a+b)m+1-a·(a+b)m=b(a+b)m;
⑤(am+bn)2=a2m+b2n,其中正确的有( )
A、2个 B、4个 C、3个 D、5个
2、=_____,(xn)2+5xn-2·xn+2=______
3、3-2+(-3)2+(π-3.14)0=___,用科学记数法表示0.0000168=___
4、已知2a·27b·37c=1998,其中a、b、c是自然数,求(a-b-c)-2014.
5、某种花粉颗粒的半径约为25 um,多少个这样的花粉颗粒顺次排列能达到1m.其中1um=10-6m.(结果用科学记数法表示)
6、小明用8个一样大的矩形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的矩形;图案甲的中间留下了边长是2cm的正方形小洞.求(a+2b)2-8ab的值.
7、七(13)、七(14)两班学生到集市上购买苹果,苹果的价格如右表:
七(14)班分两次共购买苹果70千克(第二次多于第一次),共付出189元,而七(13)班则一次购苹果70千克。
购买苹果数
不超过30千克
30千克以上但不超过50千克
50千克以上
每千克价格
3元
2.5元
2元
(1)七(13)班比甲七(14)班少付多少元?
(2)七(14)班第一次、第二次分别购买苹果多少千克?
2013年秋初一数学期末复习教学案(二)
丰富的图形世界(期末复习)
编写: 学号_____姓名_____
一、基础训练
1、圆围绕着它的一条直径旋转一周所得到的几何图形是 。
2、长方体由 个面围成,圆柱由 个面围成,圆锥由 个面围成。
3、五棱柱有 个顶点, 条棱, 个面。
4、点动成 ,线动成 。
5、把四个棱长为1cm的正方体按图所示堆放于地面,则其表面积为___cm2。
(第5题)(第6题)
6、如图的三视图所画的几何体是 。
7、用六根长度相等的火柴棒搭等边三角形,最多搭成 个。 ( )
A、2 B、3 C、4 D、5
8、正方体的平面展开图可以是下列图形中的( )
9、将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是( )
A、5条 B、6条 C、7条 D、8条
10、用一个平面去截一个正方体截面的形状不可能是 ( )
A、四边形 B、五边形 C、六边形 D、七边形
二、知识梳理
三、例题精讲
例1、(1)在图中,按照柱、锥、球分类,属于柱体一类的有___个图形,按照组成它们的面来分类,组成它们的面中至少有一个是曲的图形的有_____个
(2)有一个正方体,在它的各个面上分别涂着红、黄、蓝、绿、紫、黑六种颜色,小明、小颖和小刚三位同学从三个不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的颜色对面各是什么颜色?
例2、一张桌子上摆放着若干个碟子,从三个方向上看到的三种视图如下图所示,则这张桌子上共有碟子为( )
A、17个 B、12个 C、8个 D、6个
例3、(1)在建筑工地上,一垛垛的红砖整齐地码放着,如图所示,是几个红砖排成的几何体的俯视图,图中的数字表示的是该位置摆放的红砖的层次数,请你画出它的正视图和左视图.
2
3
2
2
2
2
1
1
1
(2)如右图,是由一些棱长都为1cm的小正方体组合
成的简单几何体.
①该几何体的表面积(含下底面)为 ;
②该几何体的主视图如图所示,请在下面方格纸中分别画
出它的左视图和俯视图.
例4、如图是用积木摆放的一组图案,观察图形并探索:第五个图案中共有____块积木,第n个图案中共有____块积木.
例5、在如图所示的12×13的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移6格后的△A1B1C1,再画出△ABC以点C为旋转中心,顺时针方向旋转90°后的△A2B2C2.
(2)在与同学交流时,你打算如何描述①中所画的△A2B2C2的位置?
四、强化训练
1、如图是一个正方体的展开图,如果正方体相对的面上标注的值相等,那么x=_____,y=_____
(第2题) (第3题)
2、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,图是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面,则“祝”、“你”、“前”分别表示正方体的___________
3、如图所示的几何体的右视图是( )
4、由一些大小相同的小正方体组成的简单几何体的正视图和俯视图,如图所示.
(1)请你画出这个几何的左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
5、一个正方体的平面展开图如图所示,如果将它恢复成原来的正方体,那么点E和点___重合,点J和点___重合.
6、若由相同的小正方体构成的立体图形的三视图如图所示:
那么,这个立体图形最少是由_____个小正方体构成的.
7、由几个小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体的主视图和左视图.
2013年秋初一数学期末复习教学案(三)
平面图形的认识(一)
编写:学号_____姓名_____
一、基础训练
1、下列说法错误的是( )
A、两点确定一条直线 B、过一点可以画无数条直线
C、过已知三点可能画一条直线 D、平角是直线
2、下列说法中正确的是( )
A、延长直线AB B、延长射线OA
C、反向延长射线OA到P,使OP=OA D、延长线段AB到C,使AB=BC
3、如图,可以用字母表示出来的不同的线段和射线的条数分别是( )
A、3和3 B、3和4
C、6和3 D、3和1
4、如果∠1和∠2是邻补角,且∠1>∠2,那么∠2的余角是( )
A、(∠1-∠2) B、∠1 C、(∠1+∠2) D、∠2
5、下列图中,∠1与∠2是对顶角的是( )
6、如果∠α等于它的余角的2倍,则∠α的补角等于_____
7、如图,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=28°,则∠EOF=_____°
8、8点30分时,时钟的时针与分针所夹的锐角是( )
A、70° B、75° C、80° D、60°
9、(1)23°30′=________°;(2)78.36°= ______°____′________″。
10、如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
(1)若∠AOC=∠AOB,则OC的方向是_______:
(2)OD是OB的反向延长线,OD的方向是_______.
二、例题讲解
例1、已知线段AB=48cm,C是线段AB的中点,D是CB的中点,点E在AB上,且CE=AC,画图并求线段DE的长.
例2、直线AB、CD交于O,OE平分∠AOC,∠COF=90°,∠BOF=42°,
求∠COE的度数。
例3、(1) 如图l所示,将书页折过去,使角顶点 A落在A′处,BC为折痕,BD
为∠A′BE的平分线,求∠CBD的度数.
(2)如图2,要用一张长方形纸折成一个纸袋,两条折痕的夹角为70°(即∠POQ=70°),将折过来的重叠部分抹上胶水,即可做成一个纸袋,则粘胶水部分所构成的∠A'OB'=______.
(图1)(图2)
例4、如图,在方格纸上有一条线段AB和一点C. ①过点C画出与AB平行的直线;
②过点C画出与AB垂直的直线.
例5、已知:如图, OA⊥OB,∠AOC=460,OM平分∠AOC,ON平 分∠BOC,则∠MON的度数为 ;
变式:(1)当00<∠AOC< 900时,∠MON的度数是 ;
(2)当900<∠AOC<1800时,∠MON的度数是 .
例6、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD。
(1)图中∠AOF的补角是 (把符合条件的角都填出来)。
(2)图中除直角相等外,还有相等的角,请写出所有相等的角:
(3)①如果∠AOD=130°.那么根据 ,
可得∠BOC= 度。
②如果,求∠EOF的度数。
例7、如图,已知∠AOB,画射线OC⊥OA,OD⊥OB.
(1)画出符合要求的图形;
(2)若∠AOB=30°,其他条件不变,则∠COD=_______;
(3)若(2)中∠AOB=m°,其他条件不变,则∠COD=_______;
(4)结合(1)中画图和(2)、(3)的结果,你能从中看出什么规律(用一句话来归纳)?
三、强化训练
1、对于直线AB、线段CD、射线EF,在下列各图中能相交的是( )
2、下列语句中,正确的是( )
A、射线AB与射线BA表示同一条射线
B、在同一平面内,经过一点有且只有一条直线与已知直线平行
C、在同一平面内,经过一点有且只有一条直线与已知直线垂直
D、直线l1∥l2,l2∥l3,则l1∥l3,理由是等量代换
3、小孩子玩玩具手枪,在瞄准时总是半闭着眼,对着准星与目标,用数学知识解释为_______.
4、下列说法:①两点之间的距离是两点间的线段;②如果两条线段没有交点,那么这两条线段所在直线也没有交点;③邻补角的两条角平分线构成一个直角;④同一平面内,过一点有且只有一条直线与已知直线垂直;⑤同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( )
A、1个 B、2个 C、3个 D、4个
5、已知∠AOB=50°,以OB为一边画∠BOC=20°,则∠AOC=____°
6、已知线段AB=20cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,则AM=_____cm
7、如图是一个马路上的人行横道线,即斑马线的示意图,请你根据图示判断在过马路时三条线路AC、AB、AD中最短的是_______.
第7题 第8题
8、如图,要把角钢①变成120°的角钢②,则角钢①上截去的缺口的度数是_______.
9、我们知道:式子|x-3|的几何意义是数轴上表示数x的点与表示数3的点之间的距离,则式子|x-2|+|x+1|的最小值是为_____
10、(1)如图1,在方格纸中有三个格点三角形(顶点在小正方形的顶点上),把三角形ABC绕点A顺时针旋转90°,可以得到三角形ADE,再将三角形ADE向左平移5格,得到三角形FHG,图中,直线AB、AD、FH两两之间有怎样的位置关系?
(2)如图2,用直尺过点A画AD⊥AB,过点C画CF⊥AB,垂足为F,并在图中标出直线AD、CF经过的格点.
同课章节目录
