2022-2023学年北师大版九年级数学上册4.8 图形的位似同步练习(含解析)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册4.8 图形的位似同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 903.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 12:18:56 | ||
图片预览



文档简介
北师大版九上 4.8 图形的位似
一、选择题(共8小题)
1. 用作位似图形的方法,可以将一个图形放大或缩小 .位似中心位置可选在
A. 原图形的外部 B. 原图形的内部 C. 原图形的边上 D. 任意位置
2. 四边形 和四边形 关于原点位似,且相似比为 ,若 的坐标为 ,则它的对应点 的坐标为
A. B.
C. 或 D. 或
3. 下列命题中,说法正确的是
A. 所有菱形都相似
B. 两边对应成比例且有一组角对应相等的两个三角形相似
C. 三角形的重心到一个顶点的距离,等于它到这个顶点对边距离的两倍
D. 斜边和直角边对应成比例,两个直角三角形相似
4. 如图所示,在正方形 中,, 分别是边 , 上的点,且 , 与 相交于点 ,则下列结论中,错误的是
A. B.
C. D.
5. 如图,正方形 的两边 , 分别在平面直角坐标系的 轴, 轴的正半轴上,正方形 与正方形 是以 的中点 为中心的位似图形,已知 ,若点 的坐标为 ,则正方形 与正方形 的相似比是
A. B. C. D.
6. 如图, 和 是以点 为位似中心的位似三角形,若 为 的中点,,则 的长为
A. B. C. D.
7. 如图所示,图中的每个小方格都是边长为 的小正方形,每个小正方形的顶点称为格点.若 与 是位似图形,且顶点都在格点上,则位似中心的坐标是
A. B. C. D.
8. 如图,在直角坐标系中,矩形 的顶点 在坐标原点,边 在 轴上, 在 轴上,如果矩形 与矩形 关于点 位似,且矩形 的面积等于矩形 面积的 ,那么点 的坐标是
A. B.
C. D.
二、填空题(共7小题)
9. 如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为 ,那么大“鱼”上对应“顶点”的坐标为 .
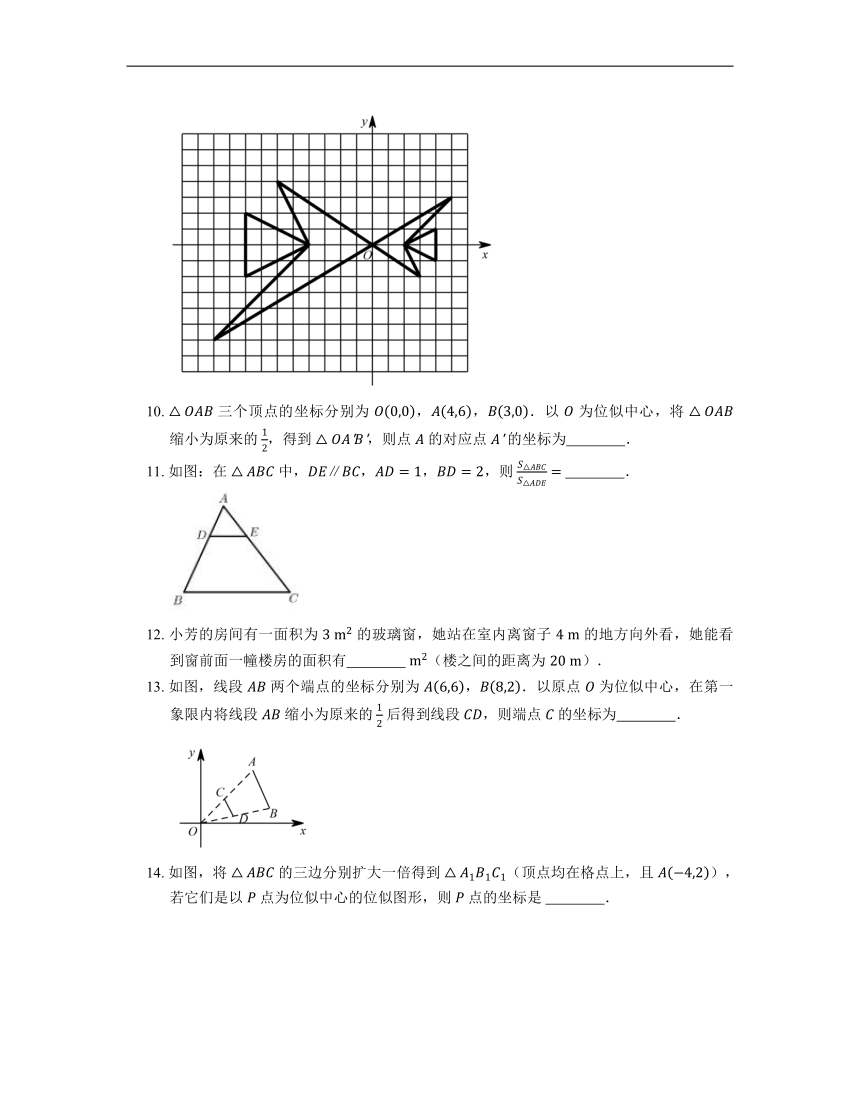
10. 三个顶点的坐标分别为 ,,.以 为位似中心,将 缩小为原来的 ,得到 ,则点 的对应点 的坐标为 .
11. 如图:在 中,,,,则 .
12. 小芳的房间有一面积为 的玻璃窗,她站在室内离窗子 的地方向外看,她能看到窗前面一幢楼房的面积有 (楼之间的距离为 ).
13. 如图,线段 两个端点的坐标分别为 ,.以原点 为位似中心,在第一象限内将线段 缩小为原来的 后得到线段 ,则端点 的坐标为 .
14. 如图,将 的三边分别扩大一倍得到 (顶点均在格点上,且 ),若它们是以 点为位似中心的位似图形,则 点的坐标是 .
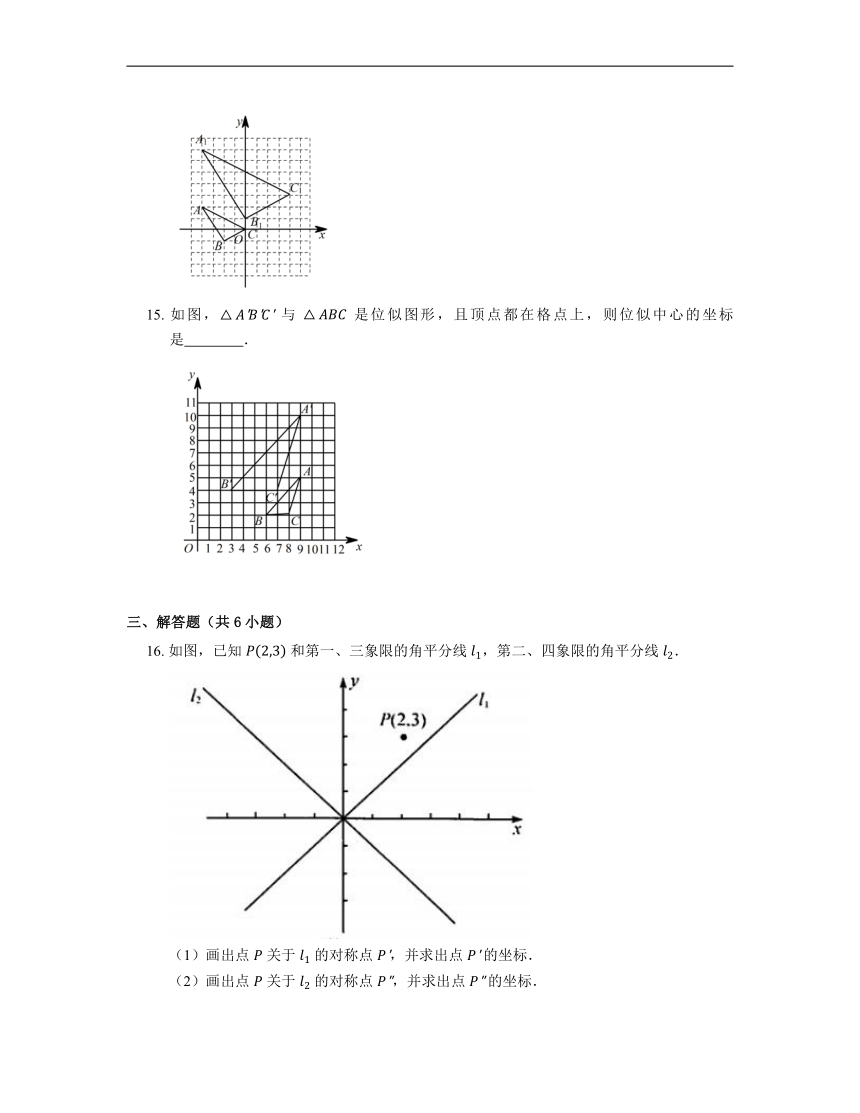
15. 如图, 与 是位似图形,且顶点都在格点上,则位似中心的坐标是 .
三、解答题(共6小题)
16. 如图,已知 和第一、三象限的角平分线 ,第二、四象限的角平分线 .
(1)画出点 关于 的对称点 ,并求出点 的坐标.
(2)画出点 关于 的对称点 ,并求出点 的坐标.
(3)从上述两题的解题过程中,你发现了什么结论
17. 如图,四边形 的一个位似图形是四边形 .且 ,,, 的对应点分别是 ,,,.图形中给出了 的对应边 所在的位置,请把四边形 其余部分补画上.
18. 用两种方法画出图中四边形 扩大为原来的 倍后的图形.
19. 如图,在四边形 内选一点 为位似中心将它放大为原来的两倍(保留作图痕迹).
20. 在平面直角坐标系中,将 ,,, 四个点用线段连接成一个图案,如图所示.
(1)如果原来四个点的纵坐标保持不变,横坐标都加上 ,将对应所得的点相应地用线段连接起来,那么所得的图案是由原来的图案进行了怎样的平移得到的
(2)如果原来四个点的横坐标保持不变,纵坐标都减去 ,将对应所得的点相应地用线段连接起来,那么所得的图案是由原来的图案进行了怎样的平移得到的
21. 如图,图中的小方格都是边长为 的正方形, 与 是以点 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点 ;
(2)求出 与 的位似比;
(3)以点 为位似中心,再画一个 ,使它与 的位似比等于 .
答案
1. D
2. C
3. D
4. C
【解析】A.四边形 是正方形,
,,
又 ,
,
,
,
故A正确;
B.,
,
,
,
,
,
故B确;
C.如图,连接 ,
假设 ,
,
,
,
,
,
又 ,
,
不可能等于 ,
假设 不成立,即 ,
故C错误;
D.,
,
,
,
故D正确.
故选C.
5. B
【解析】
在正方形 中,,
.
如图,延长 交 于点 .
点 的坐标为 ,
,,
正方形 的边长为 ,
正方形 与正方形 的相似比是 .
6. B
【解析】 为 的中点,
,
和 是以点 为位似中心的位似三角形,
,,
,
,
即 ,
.
7. C
8. D
【解析】由题意知两矩形位似比为 ,矩形 如图所示:
9.
10. 或
11.
【解析】,,
,
,
,
.
12.
【解析】如图, 为小方的眼睛位置,四边形 为窗户,四边形 为所看到的最大范围,由图可知这两个四边形是相似形,
其相似比为小芳距窗户的距离 和小芳距对面楼的距离 之比.
所以其相似比为 ,
所以 ,即 ,
解得 .
13.
14.
【解析】提示:位似中心是对应点连线的交点.
15.
16. (1) .
(2) .
(3) 略.
17.
(i)连接 , 相交于点 ,则 为位似中心;
(ii)作射线 ,;
(iii)分别过 , 作 交射线 于点 , 交射线 于点 ;
(iv)连接 ,,,得四边形 ,即为所要作的图形(如图).
18. 解法1:
如图所示.
(i)在四边形 外取一点 ;
(ii)以点 为端点作射线 、 、 、 ;
(iii)分别在射线 、 、 、 上取点 、 、 、 ,使 ,连接 、 、 、 ,则四边形 就是四边形 放大为原来的 倍后的图形.
解法2:
如图所示.
(i)在四边形 内任取一点 ;
(ii)以点 为端点作射线 、 、 、 ;
(iii)在射线 、 、 、 上取点 、 、 、 ,使 ,连接 、 、 、 ,则四边形 就是四边形 放大为原来的 倍后的图形.
19. 如图.
结论:四边形 即为所求作.
20. (1) 原来图案向右平移 个单位得到新图案;
(2) 原来图案向下平移 个单位得到新图案.
21. (1) 如图所示,连接 并延长,连接 并延长,连接 并延长,它们的交点就是位似中心 .
(2) .
(3) 在 , 的延长线上分别截取 ,,,连接 ,,,可得到 .
一、选择题(共8小题)
1. 用作位似图形的方法,可以将一个图形放大或缩小 .位似中心位置可选在
A. 原图形的外部 B. 原图形的内部 C. 原图形的边上 D. 任意位置
2. 四边形 和四边形 关于原点位似,且相似比为 ,若 的坐标为 ,则它的对应点 的坐标为
A. B.
C. 或 D. 或
3. 下列命题中,说法正确的是
A. 所有菱形都相似
B. 两边对应成比例且有一组角对应相等的两个三角形相似
C. 三角形的重心到一个顶点的距离,等于它到这个顶点对边距离的两倍
D. 斜边和直角边对应成比例,两个直角三角形相似
4. 如图所示,在正方形 中,, 分别是边 , 上的点,且 , 与 相交于点 ,则下列结论中,错误的是
A. B.
C. D.
5. 如图,正方形 的两边 , 分别在平面直角坐标系的 轴, 轴的正半轴上,正方形 与正方形 是以 的中点 为中心的位似图形,已知 ,若点 的坐标为 ,则正方形 与正方形 的相似比是
A. B. C. D.
6. 如图, 和 是以点 为位似中心的位似三角形,若 为 的中点,,则 的长为
A. B. C. D.
7. 如图所示,图中的每个小方格都是边长为 的小正方形,每个小正方形的顶点称为格点.若 与 是位似图形,且顶点都在格点上,则位似中心的坐标是
A. B. C. D.
8. 如图,在直角坐标系中,矩形 的顶点 在坐标原点,边 在 轴上, 在 轴上,如果矩形 与矩形 关于点 位似,且矩形 的面积等于矩形 面积的 ,那么点 的坐标是
A. B.
C. D.
二、填空题(共7小题)
9. 如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为 ,那么大“鱼”上对应“顶点”的坐标为 .
10. 三个顶点的坐标分别为 ,,.以 为位似中心,将 缩小为原来的 ,得到 ,则点 的对应点 的坐标为 .
11. 如图:在 中,,,,则 .
12. 小芳的房间有一面积为 的玻璃窗,她站在室内离窗子 的地方向外看,她能看到窗前面一幢楼房的面积有 (楼之间的距离为 ).
13. 如图,线段 两个端点的坐标分别为 ,.以原点 为位似中心,在第一象限内将线段 缩小为原来的 后得到线段 ,则端点 的坐标为 .
14. 如图,将 的三边分别扩大一倍得到 (顶点均在格点上,且 ),若它们是以 点为位似中心的位似图形,则 点的坐标是 .
15. 如图, 与 是位似图形,且顶点都在格点上,则位似中心的坐标是 .
三、解答题(共6小题)
16. 如图,已知 和第一、三象限的角平分线 ,第二、四象限的角平分线 .
(1)画出点 关于 的对称点 ,并求出点 的坐标.
(2)画出点 关于 的对称点 ,并求出点 的坐标.
(3)从上述两题的解题过程中,你发现了什么结论
17. 如图,四边形 的一个位似图形是四边形 .且 ,,, 的对应点分别是 ,,,.图形中给出了 的对应边 所在的位置,请把四边形 其余部分补画上.
18. 用两种方法画出图中四边形 扩大为原来的 倍后的图形.
19. 如图,在四边形 内选一点 为位似中心将它放大为原来的两倍(保留作图痕迹).
20. 在平面直角坐标系中,将 ,,, 四个点用线段连接成一个图案,如图所示.
(1)如果原来四个点的纵坐标保持不变,横坐标都加上 ,将对应所得的点相应地用线段连接起来,那么所得的图案是由原来的图案进行了怎样的平移得到的
(2)如果原来四个点的横坐标保持不变,纵坐标都减去 ,将对应所得的点相应地用线段连接起来,那么所得的图案是由原来的图案进行了怎样的平移得到的
21. 如图,图中的小方格都是边长为 的正方形, 与 是以点 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点 ;
(2)求出 与 的位似比;
(3)以点 为位似中心,再画一个 ,使它与 的位似比等于 .
答案
1. D
2. C
3. D
4. C
【解析】A.四边形 是正方形,
,,
又 ,
,
,
,
故A正确;
B.,
,
,
,
,
,
故B确;
C.如图,连接 ,
假设 ,
,
,
,
,
,
又 ,
,
不可能等于 ,
假设 不成立,即 ,
故C错误;
D.,
,
,
,
故D正确.
故选C.
5. B
【解析】
在正方形 中,,
.
如图,延长 交 于点 .
点 的坐标为 ,
,,
正方形 的边长为 ,
正方形 与正方形 的相似比是 .
6. B
【解析】 为 的中点,
,
和 是以点 为位似中心的位似三角形,
,,
,
,
即 ,
.
7. C
8. D
【解析】由题意知两矩形位似比为 ,矩形 如图所示:
9.
10. 或
11.
【解析】,,
,
,
,
.
12.
【解析】如图, 为小方的眼睛位置,四边形 为窗户,四边形 为所看到的最大范围,由图可知这两个四边形是相似形,
其相似比为小芳距窗户的距离 和小芳距对面楼的距离 之比.
所以其相似比为 ,
所以 ,即 ,
解得 .
13.
14.
【解析】提示:位似中心是对应点连线的交点.
15.
16. (1) .
(2) .
(3) 略.
17.
(i)连接 , 相交于点 ,则 为位似中心;
(ii)作射线 ,;
(iii)分别过 , 作 交射线 于点 , 交射线 于点 ;
(iv)连接 ,,,得四边形 ,即为所要作的图形(如图).
18. 解法1:
如图所示.
(i)在四边形 外取一点 ;
(ii)以点 为端点作射线 、 、 、 ;
(iii)分别在射线 、 、 、 上取点 、 、 、 ,使 ,连接 、 、 、 ,则四边形 就是四边形 放大为原来的 倍后的图形.
解法2:
如图所示.
(i)在四边形 内任取一点 ;
(ii)以点 为端点作射线 、 、 、 ;
(iii)在射线 、 、 、 上取点 、 、 、 ,使 ,连接 、 、 、 ,则四边形 就是四边形 放大为原来的 倍后的图形.
19. 如图.
结论:四边形 即为所求作.
20. (1) 原来图案向右平移 个单位得到新图案;
(2) 原来图案向下平移 个单位得到新图案.
21. (1) 如图所示,连接 并延长,连接 并延长,连接 并延长,它们的交点就是位似中心 .
(2) .
(3) 在 , 的延长线上分别截取 ,,,连接 ,,,可得到 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
