2022-2023学年人教版九年级数学上册21.3 实际问题与一元二次方程 基础卷(含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册21.3 实际问题与一元二次方程 基础卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览




文档简介
21.3 实际问题与一元二次方程(基础卷)-人教版九年级上册(含答案)
一.选择题
1.我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,创造了又一个彪炳史册的人间奇迹!某贫困村从2018年开始大力发展乡村民宿旅游产业,据统计,该村2018年乡村民宿旅游收入约为2000万元,2020年该村乡村民宿旅游收入达到3380万元,则该村2018年到2020年乡村民宿旅游收入的年平均增长率约为( )
A.20% B.25% C.30% D.35%
2.在某次冠状病毒感染中,有3只动物被感染,后来经过两轮感染后共有363只动物被感染.若每轮感染中平均一只动物会感染x只动物,则下面所列方程正确的是( )
A.3x(x+1)=363 B.3+3x+3x2=363
C.3(1+x)2=363 D.3+3(1+x)+3(1+x)2=363
3.现有x支球队参加篮球比赛,比赛采用单循环制即每个球队必须和其余球队比赛一场,共比赛了45场,则下列方程中符合题意的是( )
A.x(x﹣1)=45 B.x(x+1)=45
C.x(x﹣1)=45 D.x(x+1)=45
4.我县某村从2018年开始大力发展文旅产业,打造农家生态文化旅游.据统计,该村2018年农家生态文化旅游收入约为200万元,2020年该村农家生态文化旅游收入达到288万元.据此估计该村从2018年到2020年农家生态文化旅游收入的年平均增长率为( )
A.2% B.4.4% C.20% D.44%
5.新型冠状病毒肺炎具有人传人性,调查发现1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,则x为( )
A.14 B.15 C.16 D.17
6.某市某楼盘准备以6000元/m2的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以4860元/m2的均价开盘销售,则平均每次下调的百分率是( )
A.11% B.10% C.9% D.8%
7.某校九年级3月份中考模拟总分760分以上有300人,同学们在老师们的高效复习指导下,复习效果显著,在4月份中考模拟总分760分以上人数比3月份增长5%,且5,6月份的760分以上的人数按相同的百分率x继续上升,则6月份该校760分以上的学生人数( )
A.300(1+5%)(1+2x)人 B.300(1+5%)(1+x)2人
C.(300+5%)(300+2)人 D.300(1+5%+2x)人
8.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,则设道路的宽为xm,根据题意,列方程( )
A.32×20﹣20x﹣30x=540
B.32×20﹣20x﹣30x﹣x2=540
C.(32﹣x)(20﹣x)=540
D.32×20﹣20x﹣30x+2x2=540
9.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?( )
A.﹣10 B.10 C.8 D.9
10.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到C点后停止,点P也随之停止运动,当△PBQ的面积为15cm2时,则点P运动的时间是( )
A.3s B.3s或5s C.4s D.5s
二.填空题
.第24届北京冬奥会冰壶混合双人循环赛在冰立方举行.参加比赛的每两队之间都进行一场比赛,共要比赛45场,共有 个队参加比赛.
.某学习小组的成员互赠新年贺卡,共用去72张贺卡,则该学习小组 有名成员.
.如图,某生物兴趣小组要在长40米、宽30米的矩形园地种植蔬菜,为便于管理,要在中间开辟一横两纵共三条等宽小路,若蔬菜种植面积为1008平方米,则小路的宽为 米.
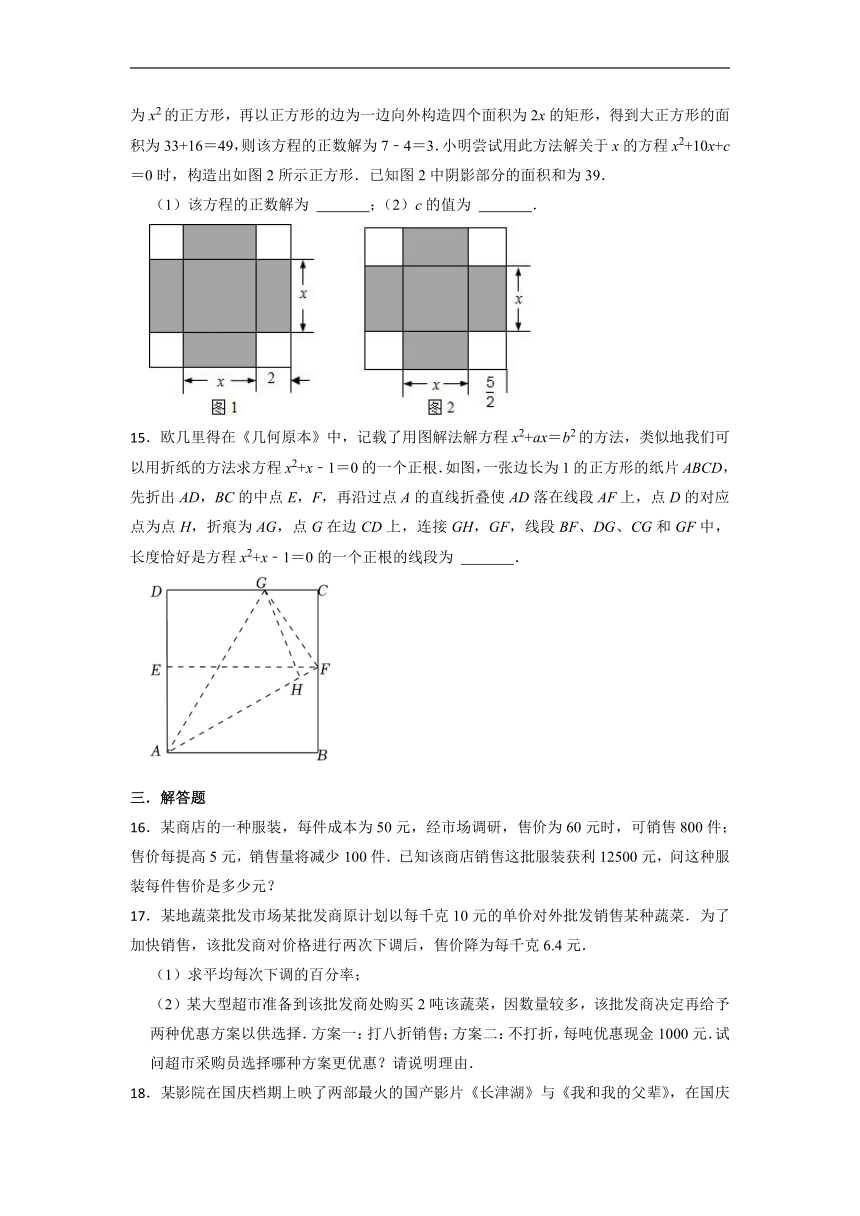
.在《代数学》中记载了求方程x2+8x=33正数解的几何方法:如图1,先构造一个面积为x2的正方形,再以正方形的边为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.小明尝试用此方法解关于x的方程x2+10x+c=0时,构造出如图2所示正方形.已知图2中阴影部分的面积和为39.
(1)该方程的正数解为 ;(2)c的值为 .
.欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地我们可以用折纸的方法求方程x2+x﹣1=0的一个正根.如图,一张边长为1的正方形的纸片ABCD,先折出AD,BC的中点E,F,再沿过点A的直线折叠使AD落在线段AF上,点D的对应点为点H,折痕为AG,点G在边CD上,连接GH,GF,线段BF、DG、CG和GF中,长度恰好是方程x2+x﹣1=0的一个正根的线段为 .
三.解答题
.某商店的一种服装,每件成本为50元,经市场调研,售价为60元时,可销售800件;售价每提高5元,销售量将减少100件.已知该商店销售这批服装获利12500元,问这种服装每件售价是多少元?
.某地蔬菜批发市场某批发商原计划以每千克10元的单价对外批发销售某种蔬菜.为了加快销售,该批发商对价格进行两次下调后,售价降为每千克6.4元.
(1)求平均每次下调的百分率;
(2)某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择.方案一:打八折销售;方案二:不打折,每吨优惠现金1000元.试问超市采购员选择哪种方案更优惠?请说明理由.
.某影院在国庆档期上映了两部最火的国产影片《长津湖》与《我和我的父辈》,在国庆档第一周,已知买3张《长津湖》的钱可以买4张《我和我的父辈》,买2张《长津湖》和3张《我和我的父辈》一共需要170元.
(1)在国庆档第一周,一张《长津湖》的票价和一张《我和我的父辈)的票价分别是多少元?
(2)在国庆档第一周《长津湖》卖出了5000张电影票,《我和我的父辈》卖出了4000张电影票.在国庆档第二周,长津湖的每张票价在第一周的基础上降低了a%,卖出电影票的数量也比第一周降低了a%,《我和我的父辈》的票价不变,数量比第一周减少a%,国庆档的第二周两部电影的票房总价比第一周两部电影的票房总价减少了2a%,其中a>0,求a的值.
.端午节前后,某商场推广一种新式粽子出售,市场调查发现:在端午节前后各一周粽子的销售情况如图中折线ABC表示销量y(个)与销售时间第x天的函数关系.线段BC表示每增加一天,销量减少40个;
(1)第14天的销量为 个?
(2)直接写出y与x的函数关系式,并写出对应的x的取值范围;
(3)若粽子的固定成本为1元/个,固定售价为3元/个;
①这些天的销售中,日利润是800元的出现在第几天?
②端午节过后的连续2天内,第1天捐款当天总利润的a%,第2天捐款当天总利润的2a%,为保证捐款后这两天的平均日利润不低于730元,求a%的最大值.
.我们把一个式子或一个式子部分改写成完全平方式或者几个完全平方式的和的形式,这种解题方法叫做配方法,配方法常常用于恒等变形、化简求值、解一元二次方程、求最值等问题.
(1)已知三角形ABC的三边长a、b、c都是正整数,并且满足a2+2b2﹣6a﹣4b+11=0,求三角形ABC的周长,你能利用配方法解决这个问题吗?
(2)某商品现在每件盈利10元,每天可卖出30件.市场调查发现:如调整价格,每涨价1元,每天要少卖1件,当每件商品涨价多少元时,每天的利润最大?
参考答案与试题解析
一.选择题
1.【解答】解:设该村2018年到2020年乡村民宿旅游收入的年平均增长率约为x,
依题意得:2000(1+x)2=3380,
解得:x1=0.3=30%,x2=﹣2.3(不合题意,舍去).
故选:C.
2.【解答】解:每轮感染中平均一只动物会感染x只动物,列方程得:3(1+x) =363,
故选:C.
3.【解答】解:∵有x支球队参加篮球比赛,每两队之间都比赛一场,
∴共比赛场数为x(x﹣1).
∴共比赛了45场,
∴x(x﹣1)=45,
故选:A.
4.【解答】解:设该村从2018年到2020年农家生态文化旅游收入的年平均增长率为x,
依题意得:200(1+x)2=288,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
故选:C.
5.【解答】解:设1人平均感染x人,
依题意可列方程:(1+x)2=225.
解得:x1=14,x2=﹣16(不合题意舍去),
即:x=14,
故选:A.
6.【解答】解:设平均每次下调的百分率为x,由题意,得
6000(1﹣x)2=4860,
解得:x1=0.1,x2=1.9(舍去).
答:平均每次下调的百分率为10%.
故选:B.
7.【解答】解:根据题意知,6月份该校760分以上的学生人数=300(1+5%)(1+x)2人.
故选:B.
8.【解答】解:设道路的宽为x,根据题意得(32﹣x)(20﹣x)=540.
故选:C.
9.【解答】解:设每一轮感染中平均每台电脑会感染x台电脑,
根据题意得:(1+x)2=81,
解得:x=8或x=﹣10(舍去).
∴每轮感染中平均一台电脑会感染8台电脑.
故选:C.
10.【解答】解:设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,
则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得,
(8﹣t)×2t=15,
解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).
∴动点P,Q运动3秒时,能使△PBQ的面积为15cm2.
故选:A.
二.填空题
.【解答】解:设共有x个队参加比赛,
依题意得:x(x﹣1)=45,
整理得:x2﹣x﹣90=0,
解得:x1=10,x2=﹣9(不合题意,舍去).
即:共有10个队参加比赛.
故答案为:10.
.【解答】解:设这个小组有x名成员,则小组内每名成员需送出(x﹣1)张贺卡,
根据题意得:x(x﹣1)=72,
解得:x1=9,x2=﹣8(不合题意,舍去).
故答案为:9.
.【解答】解:小路的宽为x米.
由题意可得:(40﹣2x)(30﹣x)=1008,
解得:x1=2,x2=48(不合题意,舍去),
答:小路的宽为2米,
故答案为:2.
.【解答】解:如图2,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为:
39+()2×4=39+25=64,
∴该方程的正数解为﹣×2=8﹣5=3,
把x=3代入方程得9+30+c=0,
解得c=﹣39.
故答案为:x=3;﹣39.
.【解答】解:设DG=m,则GC=1﹣m.
由题意可知:△ADG≌△AHG,F是BC的中点,
∴DG=GH=m,FC=0.5,
根据勾股定理得AF=.
∵S正方形=S△ABF+S△ADG+S△CGF+S△AGF,
∴1×1=×1×+×1×m+××(1﹣m)+××m,
∴m=.
∵x2+x﹣1=0的解为:x=,
∴取正值为x=.
∴这条线段是线段DG.
故答案为:DG.
三.解答题
.【解答】解:设这种服装每件售价是x元,根据题意得:
(x﹣50)(800﹣100×)=12500,
(x﹣50)(800﹣20x+1200)=12500,
x2﹣150x+5625=0,
解得x1=x2=75.
答:这种服装每件售价为75元.
.【解答】解:(1)设平均每次下调x,
根据题意,得10(1﹣x)2=6.4,
解得x=20%或x=180%(舍去),
答:平均每次下调20%;
(2)方案一更优惠,理由如下:
方案一:6.4×0.8×2000=10240(元),
方案二:6.4×2000﹣2000=10800(元),
∵10240<10800,
∴采购员选择方案一更优惠.
.【解答】解:(1)设一张《长津湖》的票价是x元,一张《我和我的父辈)的票价是y元,
由题意得,,
解得,
答:一张《长津湖》的票价是40元,一张《我和我的父辈)的票价是30元;
(2)由题意得,
解得a=0或10.
答:a的值是10.(2)由题意得,
40(1﹣a%)×5000(1﹣a%)+30×4000(1﹣a%)=(5000×40+4000×30)×(1﹣2a%),
解得a=0(舍去)或20.
答:a的值是20.
.【解答】解:(1)∵线段BC表示每增加一天,销量减少40个,
∴第14天比第十五天多40个,
∴360+40=400(个),
故答案为:400;
(2)设AB段函数解析式为y=kx+b(k≠0),
∵AB段经过(1,200),(3,300),
则,
解得:,
∴AB段函数解析式为y=50x+150;
设BC段函数解析式为y=mx+n(m≠0),
∵BC段经过(14,400),(15,360),
则,
解得:,
∴BC段函数解析式为y=﹣40x+960;
∵50x+150=﹣40x+960,
∴x=9.
∴y与x的函数关系式为y=;
(3)①设每天利润为w元,
根据题意得:w=(3﹣1)y=,
当w=800时,100x+300=800或﹣80x+1920=800,
解得x=5或x=14,
∴日利润是800元的出现在第5天和第14天;
②由题意得,端午节在第8天,端午节过后的2天为x=9和x=10,
当x=9时,w=﹣80×9+1920=1200,
当x=10时,w=﹣80×10+1920=1120,
∵第1天捐款1200×a%,第2天捐款1120×2a%,
∴(1200+1120﹣1200×a%﹣1120×2a%)÷2≥730,
解得:a%≤25%,
∴a%的最大值为25%.
.【解答】解:(1)∵a2+2b2﹣6a﹣4b+11=0,
∴a2﹣6a+9+2b2﹣4b+2=0,即(a﹣3)2+2(b﹣1)2=0,
则a﹣3=0且b﹣1=0,
解得a=3,b=1,
∴3﹣1<c<3+1,即2<c<4,
∵c是正整数,
∴c=3,
则△ABC的周长为3+1+3=7;
(2)设每件商品涨价x元,
每天的利润为(10+x)(30﹣x)
=﹣x2+20x+300
=﹣(x﹣10)2+400,
∵(x﹣10)2≥0,
∴﹣(x﹣10)2≤0,
则﹣(x﹣10)2+400≤400,
∴当x=10时,﹣(x﹣10)2+400取得最大值400,
答:当每件商品涨价10元时,每天的利润最大.
一.选择题
1.我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,创造了又一个彪炳史册的人间奇迹!某贫困村从2018年开始大力发展乡村民宿旅游产业,据统计,该村2018年乡村民宿旅游收入约为2000万元,2020年该村乡村民宿旅游收入达到3380万元,则该村2018年到2020年乡村民宿旅游收入的年平均增长率约为( )
A.20% B.25% C.30% D.35%
2.在某次冠状病毒感染中,有3只动物被感染,后来经过两轮感染后共有363只动物被感染.若每轮感染中平均一只动物会感染x只动物,则下面所列方程正确的是( )
A.3x(x+1)=363 B.3+3x+3x2=363
C.3(1+x)2=363 D.3+3(1+x)+3(1+x)2=363
3.现有x支球队参加篮球比赛,比赛采用单循环制即每个球队必须和其余球队比赛一场,共比赛了45场,则下列方程中符合题意的是( )
A.x(x﹣1)=45 B.x(x+1)=45
C.x(x﹣1)=45 D.x(x+1)=45
4.我县某村从2018年开始大力发展文旅产业,打造农家生态文化旅游.据统计,该村2018年农家生态文化旅游收入约为200万元,2020年该村农家生态文化旅游收入达到288万元.据此估计该村从2018年到2020年农家生态文化旅游收入的年平均增长率为( )
A.2% B.4.4% C.20% D.44%
5.新型冠状病毒肺炎具有人传人性,调查发现1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,则x为( )
A.14 B.15 C.16 D.17
6.某市某楼盘准备以6000元/m2的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以4860元/m2的均价开盘销售,则平均每次下调的百分率是( )
A.11% B.10% C.9% D.8%
7.某校九年级3月份中考模拟总分760分以上有300人,同学们在老师们的高效复习指导下,复习效果显著,在4月份中考模拟总分760分以上人数比3月份增长5%,且5,6月份的760分以上的人数按相同的百分率x继续上升,则6月份该校760分以上的学生人数( )
A.300(1+5%)(1+2x)人 B.300(1+5%)(1+x)2人
C.(300+5%)(300+2)人 D.300(1+5%+2x)人
8.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,则设道路的宽为xm,根据题意,列方程( )
A.32×20﹣20x﹣30x=540
B.32×20﹣20x﹣30x﹣x2=540
C.(32﹣x)(20﹣x)=540
D.32×20﹣20x﹣30x+2x2=540
9.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?( )
A.﹣10 B.10 C.8 D.9
10.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到C点后停止,点P也随之停止运动,当△PBQ的面积为15cm2时,则点P运动的时间是( )
A.3s B.3s或5s C.4s D.5s
二.填空题
.第24届北京冬奥会冰壶混合双人循环赛在冰立方举行.参加比赛的每两队之间都进行一场比赛,共要比赛45场,共有 个队参加比赛.
.某学习小组的成员互赠新年贺卡,共用去72张贺卡,则该学习小组 有名成员.
.如图,某生物兴趣小组要在长40米、宽30米的矩形园地种植蔬菜,为便于管理,要在中间开辟一横两纵共三条等宽小路,若蔬菜种植面积为1008平方米,则小路的宽为 米.
.在《代数学》中记载了求方程x2+8x=33正数解的几何方法:如图1,先构造一个面积为x2的正方形,再以正方形的边为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.小明尝试用此方法解关于x的方程x2+10x+c=0时,构造出如图2所示正方形.已知图2中阴影部分的面积和为39.
(1)该方程的正数解为 ;(2)c的值为 .
.欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地我们可以用折纸的方法求方程x2+x﹣1=0的一个正根.如图,一张边长为1的正方形的纸片ABCD,先折出AD,BC的中点E,F,再沿过点A的直线折叠使AD落在线段AF上,点D的对应点为点H,折痕为AG,点G在边CD上,连接GH,GF,线段BF、DG、CG和GF中,长度恰好是方程x2+x﹣1=0的一个正根的线段为 .
三.解答题
.某商店的一种服装,每件成本为50元,经市场调研,售价为60元时,可销售800件;售价每提高5元,销售量将减少100件.已知该商店销售这批服装获利12500元,问这种服装每件售价是多少元?
.某地蔬菜批发市场某批发商原计划以每千克10元的单价对外批发销售某种蔬菜.为了加快销售,该批发商对价格进行两次下调后,售价降为每千克6.4元.
(1)求平均每次下调的百分率;
(2)某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择.方案一:打八折销售;方案二:不打折,每吨优惠现金1000元.试问超市采购员选择哪种方案更优惠?请说明理由.
.某影院在国庆档期上映了两部最火的国产影片《长津湖》与《我和我的父辈》,在国庆档第一周,已知买3张《长津湖》的钱可以买4张《我和我的父辈》,买2张《长津湖》和3张《我和我的父辈》一共需要170元.
(1)在国庆档第一周,一张《长津湖》的票价和一张《我和我的父辈)的票价分别是多少元?
(2)在国庆档第一周《长津湖》卖出了5000张电影票,《我和我的父辈》卖出了4000张电影票.在国庆档第二周,长津湖的每张票价在第一周的基础上降低了a%,卖出电影票的数量也比第一周降低了a%,《我和我的父辈》的票价不变,数量比第一周减少a%,国庆档的第二周两部电影的票房总价比第一周两部电影的票房总价减少了2a%,其中a>0,求a的值.
.端午节前后,某商场推广一种新式粽子出售,市场调查发现:在端午节前后各一周粽子的销售情况如图中折线ABC表示销量y(个)与销售时间第x天的函数关系.线段BC表示每增加一天,销量减少40个;
(1)第14天的销量为 个?
(2)直接写出y与x的函数关系式,并写出对应的x的取值范围;
(3)若粽子的固定成本为1元/个,固定售价为3元/个;
①这些天的销售中,日利润是800元的出现在第几天?
②端午节过后的连续2天内,第1天捐款当天总利润的a%,第2天捐款当天总利润的2a%,为保证捐款后这两天的平均日利润不低于730元,求a%的最大值.
.我们把一个式子或一个式子部分改写成完全平方式或者几个完全平方式的和的形式,这种解题方法叫做配方法,配方法常常用于恒等变形、化简求值、解一元二次方程、求最值等问题.
(1)已知三角形ABC的三边长a、b、c都是正整数,并且满足a2+2b2﹣6a﹣4b+11=0,求三角形ABC的周长,你能利用配方法解决这个问题吗?
(2)某商品现在每件盈利10元,每天可卖出30件.市场调查发现:如调整价格,每涨价1元,每天要少卖1件,当每件商品涨价多少元时,每天的利润最大?
参考答案与试题解析
一.选择题
1.【解答】解:设该村2018年到2020年乡村民宿旅游收入的年平均增长率约为x,
依题意得:2000(1+x)2=3380,
解得:x1=0.3=30%,x2=﹣2.3(不合题意,舍去).
故选:C.
2.【解答】解:每轮感染中平均一只动物会感染x只动物,列方程得:3(1+x) =363,
故选:C.
3.【解答】解:∵有x支球队参加篮球比赛,每两队之间都比赛一场,
∴共比赛场数为x(x﹣1).
∴共比赛了45场,
∴x(x﹣1)=45,
故选:A.
4.【解答】解:设该村从2018年到2020年农家生态文化旅游收入的年平均增长率为x,
依题意得:200(1+x)2=288,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
故选:C.
5.【解答】解:设1人平均感染x人,
依题意可列方程:(1+x)2=225.
解得:x1=14,x2=﹣16(不合题意舍去),
即:x=14,
故选:A.
6.【解答】解:设平均每次下调的百分率为x,由题意,得
6000(1﹣x)2=4860,
解得:x1=0.1,x2=1.9(舍去).
答:平均每次下调的百分率为10%.
故选:B.
7.【解答】解:根据题意知,6月份该校760分以上的学生人数=300(1+5%)(1+x)2人.
故选:B.
8.【解答】解:设道路的宽为x,根据题意得(32﹣x)(20﹣x)=540.
故选:C.
9.【解答】解:设每一轮感染中平均每台电脑会感染x台电脑,
根据题意得:(1+x)2=81,
解得:x=8或x=﹣10(舍去).
∴每轮感染中平均一台电脑会感染8台电脑.
故选:C.
10.【解答】解:设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,
则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得,
(8﹣t)×2t=15,
解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).
∴动点P,Q运动3秒时,能使△PBQ的面积为15cm2.
故选:A.
二.填空题
.【解答】解:设共有x个队参加比赛,
依题意得:x(x﹣1)=45,
整理得:x2﹣x﹣90=0,
解得:x1=10,x2=﹣9(不合题意,舍去).
即:共有10个队参加比赛.
故答案为:10.
.【解答】解:设这个小组有x名成员,则小组内每名成员需送出(x﹣1)张贺卡,
根据题意得:x(x﹣1)=72,
解得:x1=9,x2=﹣8(不合题意,舍去).
故答案为:9.
.【解答】解:小路的宽为x米.
由题意可得:(40﹣2x)(30﹣x)=1008,
解得:x1=2,x2=48(不合题意,舍去),
答:小路的宽为2米,
故答案为:2.
.【解答】解:如图2,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为:
39+()2×4=39+25=64,
∴该方程的正数解为﹣×2=8﹣5=3,
把x=3代入方程得9+30+c=0,
解得c=﹣39.
故答案为:x=3;﹣39.
.【解答】解:设DG=m,则GC=1﹣m.
由题意可知:△ADG≌△AHG,F是BC的中点,
∴DG=GH=m,FC=0.5,
根据勾股定理得AF=.
∵S正方形=S△ABF+S△ADG+S△CGF+S△AGF,
∴1×1=×1×+×1×m+××(1﹣m)+××m,
∴m=.
∵x2+x﹣1=0的解为:x=,
∴取正值为x=.
∴这条线段是线段DG.
故答案为:DG.
三.解答题
.【解答】解:设这种服装每件售价是x元,根据题意得:
(x﹣50)(800﹣100×)=12500,
(x﹣50)(800﹣20x+1200)=12500,
x2﹣150x+5625=0,
解得x1=x2=75.
答:这种服装每件售价为75元.
.【解答】解:(1)设平均每次下调x,
根据题意,得10(1﹣x)2=6.4,
解得x=20%或x=180%(舍去),
答:平均每次下调20%;
(2)方案一更优惠,理由如下:
方案一:6.4×0.8×2000=10240(元),
方案二:6.4×2000﹣2000=10800(元),
∵10240<10800,
∴采购员选择方案一更优惠.
.【解答】解:(1)设一张《长津湖》的票价是x元,一张《我和我的父辈)的票价是y元,
由题意得,,
解得,
答:一张《长津湖》的票价是40元,一张《我和我的父辈)的票价是30元;
(2)由题意得,
解得a=0或10.
答:a的值是10.(2)由题意得,
40(1﹣a%)×5000(1﹣a%)+30×4000(1﹣a%)=(5000×40+4000×30)×(1﹣2a%),
解得a=0(舍去)或20.
答:a的值是20.
.【解答】解:(1)∵线段BC表示每增加一天,销量减少40个,
∴第14天比第十五天多40个,
∴360+40=400(个),
故答案为:400;
(2)设AB段函数解析式为y=kx+b(k≠0),
∵AB段经过(1,200),(3,300),
则,
解得:,
∴AB段函数解析式为y=50x+150;
设BC段函数解析式为y=mx+n(m≠0),
∵BC段经过(14,400),(15,360),
则,
解得:,
∴BC段函数解析式为y=﹣40x+960;
∵50x+150=﹣40x+960,
∴x=9.
∴y与x的函数关系式为y=;
(3)①设每天利润为w元,
根据题意得:w=(3﹣1)y=,
当w=800时,100x+300=800或﹣80x+1920=800,
解得x=5或x=14,
∴日利润是800元的出现在第5天和第14天;
②由题意得,端午节在第8天,端午节过后的2天为x=9和x=10,
当x=9时,w=﹣80×9+1920=1200,
当x=10时,w=﹣80×10+1920=1120,
∵第1天捐款1200×a%,第2天捐款1120×2a%,
∴(1200+1120﹣1200×a%﹣1120×2a%)÷2≥730,
解得:a%≤25%,
∴a%的最大值为25%.
.【解答】解:(1)∵a2+2b2﹣6a﹣4b+11=0,
∴a2﹣6a+9+2b2﹣4b+2=0,即(a﹣3)2+2(b﹣1)2=0,
则a﹣3=0且b﹣1=0,
解得a=3,b=1,
∴3﹣1<c<3+1,即2<c<4,
∵c是正整数,
∴c=3,
则△ABC的周长为3+1+3=7;
(2)设每件商品涨价x元,
每天的利润为(10+x)(30﹣x)
=﹣x2+20x+300
=﹣(x﹣10)2+400,
∵(x﹣10)2≥0,
∴﹣(x﹣10)2≤0,
则﹣(x﹣10)2+400≤400,
∴当x=10时,﹣(x﹣10)2+400取得最大值400,
答:当每件商品涨价10元时,每天的利润最大.
同课章节目录
