2022-2023学年人教版九年级数学上册22.1 二次函数的图象和性质 精选题 (含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册22.1 二次函数的图象和性质 精选题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 418.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 12:25:32 | ||
图片预览




文档简介
22.1 二次函数的图象和性质(精选题)-人教版九年级上册(含答案)
一.选择题
.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是( )
A.s≥3 B.3<s<8 C.s≤3 D.s≥9
.已知二次函数y=2x2﹣4x﹣1在0≤x≤a时,y取得的最大值为15,则a的值为( )
A.1 B.2 C.3 D.4
.已知二次函数y=ax2+bx+c,当x1=0,x2=1,x3=3时,它们对应的函数值分别为y1,y2,y3,且y1=y3>y2,则( )
A.a>0,3a+b=0 B.a<0,3a+b=0
C.a>0,3a+2b=0 D.a<0,3a+2b=0
.抛物线y=﹣(x﹣1)2+3的顶点坐标是( )
A.(﹣1,3) B.(1,3) C.(﹣1,﹣3) D.(1,﹣3)
.如图,是二次函数y=ax2+bx+c的图象,下列结论:
①二次三项式ax2+bx+c的最大值为4;
②b=﹣2;
③使y≤3成立的x的取值范围是x≤﹣2或x≥1;
④一元二次方程ax2+bx+c=m(m<4)的两根之和为﹣2.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
.二次函数y=(x+m)2+n的图象如图所示,则一次函数y=mx+n的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
A.abc>0 B.b2>4ac
C.当﹣3≤x≤1时,y≥0 D.3a+c=1
.表一记录了二次函数y=ax2+bx+2(a≠0)中两个变量x与y的6组对应值,其中﹣5<x1<x2<1<x3<3.
表一
x … ﹣5 x1 x2 1 x3 3 …
y … m 0 2 0 n m …
根据表中信息,当时,直线y=k与该二次函数图象有两个公共点,则k的取值范围为( )
A. B. C. D.
.对于题目“一段抛物线y=﹣x2+3x+c(0≤x≤3)与直线y=x+2有唯一公共点.若c为整数,确定所有c的值”.甲的结果是c=1,乙的结果是c=3或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
.如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+n(n为常数)与扇形OAB的边界总有两个公共点,则n的取值范围是( )
A.n>﹣4 B. C. D.
二.填空题
.已知点A是直线上一动点,以点A为顶点的抛物线y=(x﹣m)2+h交y轴于点B,作点B关于x轴的对称点C,连接AB、AC.若△ABC是直角三角形,则点A的坐标为 .
.二次函数y=x2﹣4x+5的对称轴为x= .
.已知y关于x的二次函数y=x2﹣2mx+(m+1)2(m为常数)的顶点坐标为(h,k)
(1)k关于h的函数解析式为 .
(2)若抛物线不经过第三象限,且在﹣2≤x≤2时,二次函数最小值和最大值和为,则m= .
.在平面直角坐标系xOy中,A(﹣2,3),B(1,0),抛物线的解析式为y=ax2+bx+3.
(1)若此抛物线经过A,B两点,则a﹣b= ;
(2)若此抛物线经过点A,且与线段AB有两个不同的交点,则a的取值范围是 .
.点M(m,n)在以y轴为对称轴的二次函数y=﹣x2+bx+2的图象上,则m+n的最大值为 .
三.解答题
.如图,抛物线y=﹣+与x轴交于A、B两点,与y轴交于C点.
(1)求A、B、C三点的坐标;
(2)证明△ABC为直角三角形.
.如图,直线y=﹣x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+x+c经过B,C两点.
(1)求抛物线的解析式;
(2)E是直线BC上方抛物线上的一动点,当点E到直线BC的距离最大时,求点E的坐标;
(3)Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,B,C为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
.在平面直角坐标系中,已知抛物线经过A(﹣2,0),两点,且与y轴交于点C,点B是该抛物线的顶点.
(1)求抛物线L1的表达式;
(2)将L1平移后得到抛物线L2,点D,E在L2上(点D在点E的上方),若以点A,C,D,E为顶点的四边形是正方形,求抛物线L2的解析式.
.已知抛物线y=ax2+c(a≠0)过点P(3,0),Q(1,4).
(1)求抛物线的解析式;
(2)点A在直线PQ上且在第一象限内,过A作AB⊥x轴于B,以AB为斜边在其左侧作等腰直角△ABC.
①若A与Q重合,求C到抛物线对称轴的距离;
②点C能否落在抛物线上,若能求点C的坐标,若不能说明理由.
.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于C点,D为抛物线顶点.连接AD,交y轴于点E,P是抛物线上的一个动点.
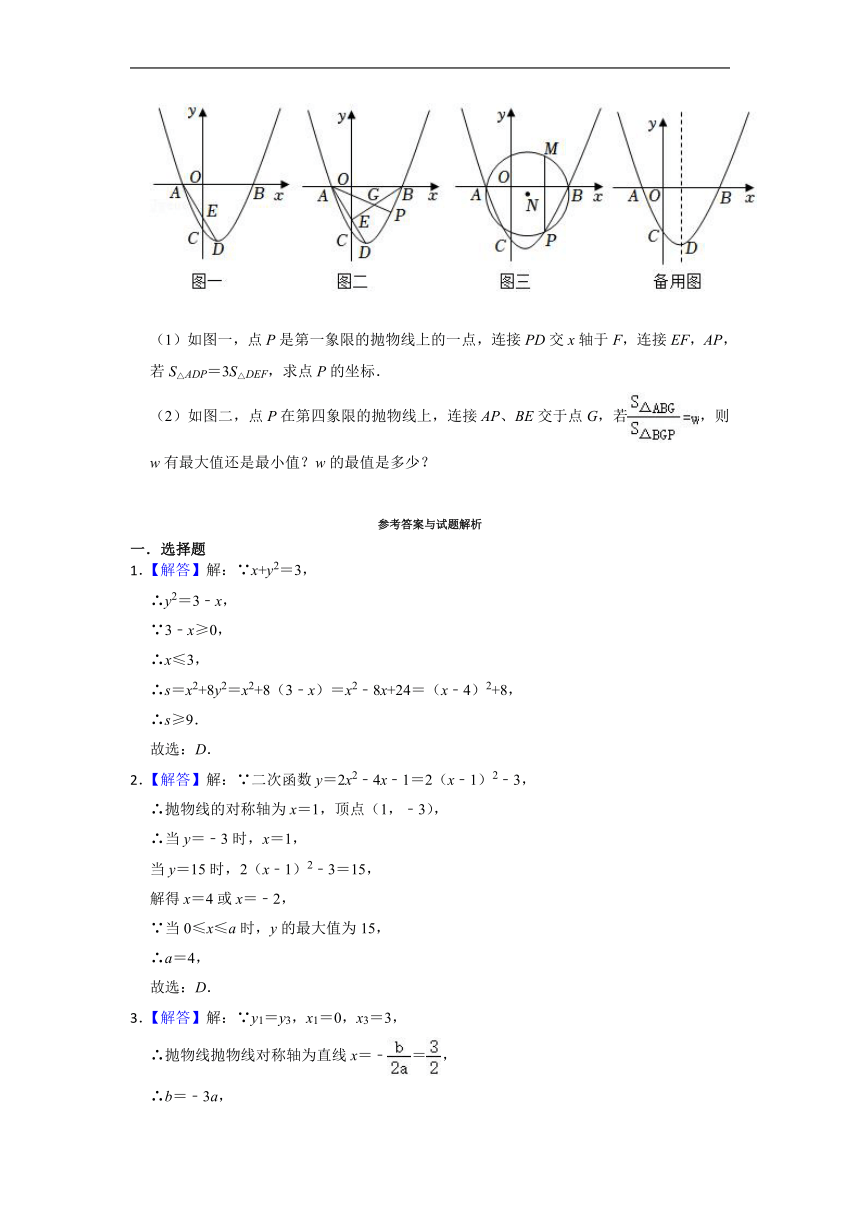
(1)如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接EF,AP,若S△ADP=3S△DEF,求点P的坐标.
(2)如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w有最大值还是最小值?w的最值是多少?
参考答案与试题解析
一.选择题
.【解答】解:∵x+y2=3,
∴y2=3﹣x,
∵3﹣x≥0,
∴x≤3,
∴s=x2+8y2=x2+8(3﹣x)=x2﹣8x+24=(x﹣4)2+8,
∴s≥9.
故选:D.
.【解答】解:∵二次函数y=2x2﹣4x﹣1=2(x﹣1)2﹣3,
∴抛物线的对称轴为x=1,顶点(1,﹣3),
∴当y=﹣3时,x=1,
当y=15时,2(x﹣1)2﹣3=15,
解得x=4或x=﹣2,
∵当0≤x≤a时,y的最大值为15,
∴a=4,
故选:D.
.【解答】解:∵y1=y3,x1=0,x3=3,
∴抛物线抛物线对称轴为直线x=﹣=,
∴b=﹣3a,
∵x1<x2<x3,y3>y2,
∴抛物线开口向上,即a>0,
∴b<0,
∴3a+b=0,
故选:A.
.【解答】解:∵y=﹣(x﹣1)2+3,
∴抛物线顶点坐标为(1,3),
故选:B.
.【解答】解:由图象经过(﹣3,0),(1,0)可设抛物线解析式为y=a(x+3)(x﹣1),
将(0,3)代入y=a(x+3)(x﹣1)得3=﹣3a,
解得a=﹣1,
∴y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3=﹣(x+1)2+4,
∴函数最大值为4,b=﹣2.①②正确.
∵抛物线经过(﹣3,0),(1,0),
∴抛物线对称轴为直线x=﹣1,
∵抛物线经过(0,3),
∴抛物线经过(﹣2,3),
∴y≤3时,x≤﹣2或x≥0,③不正确.
当m<4时,方程ax2+bx+c=m有2个不相等的实数根,
∵抛物线关于直线x=﹣1对称,
∴x1+x2=2×(﹣1)=﹣2,④正确.
故选:C.
.【解答】解:∵y=(x+m)2+n,
∴抛物线顶点坐标为(﹣m,n),
∵抛物线顶点在第四象限,
∴m<0,n<0,
∴直线y=mx+n经过第二,三,四象限,
故选:D.
.【解答】解:∵抛物线对称轴为直线x=﹣<0,
∴ab>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc>0.选项A正确.
∵抛物线与x轴有两个不同交点,
∴Δ=b2﹣4ac>0,
∴b2>4ac,选项B正确.
∵抛物线经过(1,0),对称轴为直线x=﹣1,
∴抛物线经过(﹣3,0),
∴﹣3≤x≤1时,y≥0,选项C正确.
∵﹣=﹣1,
∴b=2a,
∵抛物线经过(1,0),
∴a+b+c=3a+c=0,选项D错误.
故选:D.
.【解答】解:∵抛物线经过(﹣5,m),(3,m),
∴抛物线对称轴为直线x=﹣=﹣1,
∴b=2a,y=ax2+2ax+2,
将(1,0)代入y=ax2+2ax+2得0=a+2a+2,
解得a=﹣,
∴y=﹣x2﹣x+2=﹣(x+1)2+,
∴x=﹣1时,y=为函数最大值,
将x=﹣代入y=﹣x2﹣x+2得y=,
将x=0代入代入y=﹣x2﹣x+2得y=2,
∴2<k<满足题意.
故选:C.
.【解答】解:∵一段抛物线y=﹣x2+3x+c(0≤x≤3)与直线y=x+2有唯一公共点,
∴分两种情况:
如图1,抛物线与直线相切,
联立解析式,
∴x2﹣2x+2﹣c=0,
∴Δ=(﹣2)2﹣4(2﹣c)=0,
解得:c=1,
如图2,抛物线与直线相交,且在0≤x≤3上只有一个交点,
此时,两个临界点分别为(0,2),(3,5)在抛物线上,
∴2<c≤5,
∵c为整数,
∴c=3,4,5,
综上所述,c=1,3,4,5,
故选:D.
.【解答】解:∵∠AOB=45°,
∴OA所在直线为y=x,
令x2+n=x,整理得x2﹣x+n=0,
当Δ=1﹣4n=0时,抛物线与线段OA只有1个交点,
解得n=,
当n<时,抛物线向下移动,
当抛物线经过B(2,0)时,0=4+n,
解得n=﹣4,
∴﹣4<n<.
故选:C.
二.填空题
.【解答】解:抛物线y=(x﹣m)2+h的顶点A(m,h),
当x=0时,y=m2+h,
∴A(m,h),B(0,m2+h),
当△ABC是直角三角形时,可能∠BAC=90°或∠ACB=90°,
当∠BAC=90°时,
∵B关于x轴的对称点是C,
∴OB=OC,
∴OA=OB=OC,
∴m2+h2=(m2+h)2①,
∵A在直线y=x上,
∴h=m,代入①得:
m2+m2=,
解得m=0(舍去)或m=﹣或m=,
当m=﹣时,h=﹣1,
当m=时,h=,
∴A(﹣,﹣1)或(,).
当∠ACB=90°时,
yA=yC,
∴m=﹣m2﹣,
∴m=0(舍去)或m=﹣,
∴h=﹣×=﹣,
∴A(﹣,).
故答案为:(﹣,﹣),(﹣,﹣1)或(,).
.【解答】解:∵y=x2﹣4x+5,
∴抛物线对称轴为直线x=﹣=2,
故答案为:2.
.【解答】解:(1)∵y=x2﹣2mx+(m+1)2=(x﹣m)2+2m+1,
∴h=m,k=2m+1,
∴k关于h的函数解析式为k=2h+1,
故答案为:k=2h+1;
(2)令x=0,则y=(m+1)2,
∴抛物线与y轴的交点为(0,(m+1)2).
∵(m+1)2≥0.
∵抛物线不经过第三象限,抛物线的对称轴为直线x=m,
∴m>0.
①当m≥2时,
∵抛物线的开口方向向上,
∴在﹣2≤x≤2时,当x=﹣2时,函数取最大值为y=4+4m+(m+1)2=m2+6m+5,
当x=2时,函数取最小值为y=4﹣4m+(m+1)2=m2﹣2m+5,
∵二次函数最小值和最大值和为,
∴m2+6m+5+m2﹣2m+5=,
即:2m2+4m﹣=0,
解得:m=或(不合题意,舍去),
∴此种情况不存在;
②当0<m<2时,
在﹣2≤x≤2时,当x=﹣2时,函数取最大值为y=4+4m+(m+1)2=m2+6m+5,
当x=m时,函数取最小值为y=2m+1,
∵二次函数最小值和最大值和为,
∴m2+6m+5+2m+1=,
解得:m=或m=﹣(不合题意,舍去),
∴m=.
综上,在﹣2≤x≤2时,二次函数最小值和最大值和为,则m=.
故答案为:.
.【解答】解:(1)将(﹣2,3),(1,0)代入y=ax2+bx+3得,
解得,
∴a﹣b=1.
故答案为:1.
(2)将(﹣2,3)代入y=ax2+bx+3得3=4a﹣2b+3,
∴4a﹣2b=0,
∴b=2a,
∴y=ax2+2ax+3,
∵﹣=﹣1,
∴抛物线对称轴为直线x=﹣1,
将x=﹣1代入y=ax2+2ax+3得y=﹣a+3,
∴抛物线顶点坐标为(﹣1,﹣a+3),
设直线AB解析式为y=kx+b,
将(﹣2,3),(1,0)代入y=kx+b得,
解得,
∴y=﹣x+1,
令ax2+2ax+3=﹣x+1,整理得ax2+(2a+1)x+2=0,
∴Δ=(2a+1)2﹣8a=(2a﹣1)2,
∴a=时,抛物线与直线相切,如图,
当a增大时,抛物线顶点向下移动,抛物线开口变小,符合题意,
∴a>.
当a<0时,抛物线开口向下,
当抛物线经过点B时,由(1)可得a=﹣1,如图,
当a减小时,抛物线顶点向上移动,开口变小,符合题意,
∴a≤﹣1,
故答案为:a>或a≤﹣1.
.【解答】解:∵抛物线y=﹣x2+bx+2的对称轴为y轴,
∴﹣=0,即b=0,
∴y=﹣x2+2,
将(m,n)代入y=﹣x2+2得n=﹣m2+2,
∴m+n=﹣m2﹣m+2=﹣(m+)2+,
∴m=﹣时,m+n最大值为.
故答案为:.
三.解答题
.【解答】(1)解:对于抛物线y=﹣+,当y=0时,则﹣+=0,
解得x1=﹣,x2=2;
当x=0时,y=2,
∴A(﹣,0),B(2,0),C(0,2).
(2)证明:连接AC,BC,
∵OA=,OB=2,∠AOC=∠BOC=90°,
∴AC2=()2+22=6,BC2=(2)2+22=12,
∴AC2+BC2=6+12=18;
∵AB=2﹣(﹣)=3,
∴AB2=(3)2=18,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
.【解答】解:(1)∵直线y=﹣x+4与x轴交于点C,与y轴交于点B,
∴点B,C的坐标分别为B(0,4),C(4,0),
把点B(0,4)和点C(4,0)代入抛物线y=ax2+x+c,
得:,
解之,得,
∴抛物线的解析式为.
(2)∵BC为定值,
∴当△BEC的面积最大时,点E到BC的距离最大.
如图,过点E作EG∥y轴,交直线BC于点G.
设点E的坐标为,则点G的坐标为(m,﹣m+4),
∴,
∴,
∴当m=2时,S△BEC最大,此时点E到BC的距离就最大.此时点E的坐标为(2,4).
(3)存在.由抛物线可得对称轴是直线x=1.
∵Q是抛物线对称轴上的动点,∴点Q的横坐标为1.
①当BC为边时,点B到点C的水平距离是4,
∴点Q到点P的水平距离也是4.
∴点P的横坐标是5或﹣3,∴点P的坐标为或;
②当BC为对角线时,点Q到点C的水平距离是3,
∴点B到点P的水平距离也是3,∴点P的坐标为.
综上所述,在抛物线上存在点P,使得以P,Q,B,C为顶点的四边形是平行四边形,
点P的坐标是或或.
.【解答】解:(1)设抛物线L1的表达式是,
∵抛物线L1过点A(﹣2,0),
∴,
解得,
∴.
即抛物线L1的表达式是;
(2)令x=0,则y=﹣2,∴C(0,﹣2).
Ⅰ.当AC为正方形的对角线时,如图所示,
∵AE3=E3C=CD3=D3A=2,
∴点D3的坐标为(0,0),点E3的坐标为(﹣2,﹣2).
设,则,
解得即抛物线L2的解析式是.
Ⅱ.当AC为边时,分两种情况,
如图,第①种情况,点D1,E1在AC的右上角时.
∵AO=CO=E1O=D1O=2,∴点D1的坐标为(0,2),点E1的坐标为(2,0).
设,
则,
解得:,
即抛物线L2的解析式是.
第②种情况,点D2E2在AC的左下角时,过点D2作D2M⊥x轴,
则有△AD2M≌△AD1O,
∴AO=AM,D1O=D2M.
过E2作E2N⊥y轴,同理可得,△CE2N≌△CE1O,
∴CO=CN,E1O=E2N.
则点D2的坐标为(﹣4,﹣2),点E2的坐标为(﹣2,﹣4),
设,
则,
解得,
即抛物线L2的解析式是.
综上所述:L2的表达式为:,或.
.【解答】解:(1)将P(3,0),Q(1,4)代入y=ax2+c,
∴,
解得,
∴y=﹣x2+;
(2)①∵A与Q重合,
∴A(1,4),
∵AB⊥x轴,
∴AB=4,
∵△ABC是AB为斜边的等腰直角三角形,
∴C点到AB的距离为2,
∵抛物线的对称轴为y轴,
∴C点到抛物线对称轴的距离为1;
②点C能落在抛物线上,理由如下;
设直线PQ的解析式为y=kx+b,
∴,
解得,
∴y=﹣2x+6,
设A(t,﹣2t+6)(0<t<3),
∴AB=﹣2t+6,
∴C点到AB的距离为(﹣2t+6)=﹣t+3,
∴C(2t﹣3,﹣t+3),
将点C代入y=﹣x2+,
可得﹣(2t﹣3)2+=﹣t+3,
解得t=3(舍)或t=,
∴C(﹣2,).
.【解答】解:∵抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于C点,D为抛物线顶点,
∴令x=0,解得y=﹣3,则C(0,﹣3),
令y=0,则x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4),
设直线AD的解析式为y=kx+b(k≠0),
代入A(﹣1,0),D(1,﹣4)得:,
解得,
∴y=﹣2x﹣2,
令x=0,则y=﹣2,
∴E(0,﹣2),
∴,
∴AE=ED,
∴S△FAE=S△FED,
∵S△ADP=3S△DEF,
∴S△APF=S△ADP﹣S△AFD=3S△DEF﹣S△AFD=3S△DEF﹣2S△DEF=S△DEF=S△AEF,
∵OE⊥AF,AF=AF,
∴OE=yp=2,
依题意,设P(m,m2﹣2m﹣3)(m>3),
∴m2﹣2m﹣3=2,
解得(舍),
∴;
(2)∵点P在第四象限的抛物线上,AP、BE交于点G,设P(m,m2﹣2m﹣3)(0<m<3),
设直线AP的解析式为y=cx+d,
代入A(﹣1,0),P(m,m2﹣2m﹣3)得:,
∵0<m<3,
∴m+1≠0,
解得:,
∴直线AP的解析式为y=(m﹣3)x+m﹣3,
设直线BE的解析式为y=k1x+b1,
代入B(3,0),E(0,﹣2)得:,
解得:,
∴直线BE的解析式为,
联立,解得,
∴,
∵0<m<3,
∴m﹣3≠0,
∴=,
令,
∵﹣3<0,
∴z存在最大值,则w存在最小值,
当时,z存在最大值,最大值为,则w的最小值为,
∴w有最小值,w的最小值是.
一.选择题
.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是( )
A.s≥3 B.3<s<8 C.s≤3 D.s≥9
.已知二次函数y=2x2﹣4x﹣1在0≤x≤a时,y取得的最大值为15,则a的值为( )
A.1 B.2 C.3 D.4
.已知二次函数y=ax2+bx+c,当x1=0,x2=1,x3=3时,它们对应的函数值分别为y1,y2,y3,且y1=y3>y2,则( )
A.a>0,3a+b=0 B.a<0,3a+b=0
C.a>0,3a+2b=0 D.a<0,3a+2b=0
.抛物线y=﹣(x﹣1)2+3的顶点坐标是( )
A.(﹣1,3) B.(1,3) C.(﹣1,﹣3) D.(1,﹣3)
.如图,是二次函数y=ax2+bx+c的图象,下列结论:
①二次三项式ax2+bx+c的最大值为4;
②b=﹣2;
③使y≤3成立的x的取值范围是x≤﹣2或x≥1;
④一元二次方程ax2+bx+c=m(m<4)的两根之和为﹣2.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
.二次函数y=(x+m)2+n的图象如图所示,则一次函数y=mx+n的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
A.abc>0 B.b2>4ac
C.当﹣3≤x≤1时,y≥0 D.3a+c=1
.表一记录了二次函数y=ax2+bx+2(a≠0)中两个变量x与y的6组对应值,其中﹣5<x1<x2<1<x3<3.
表一
x … ﹣5 x1 x2 1 x3 3 …
y … m 0 2 0 n m …
根据表中信息,当时,直线y=k与该二次函数图象有两个公共点,则k的取值范围为( )
A. B. C. D.
.对于题目“一段抛物线y=﹣x2+3x+c(0≤x≤3)与直线y=x+2有唯一公共点.若c为整数,确定所有c的值”.甲的结果是c=1,乙的结果是c=3或4,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
.如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+n(n为常数)与扇形OAB的边界总有两个公共点,则n的取值范围是( )
A.n>﹣4 B. C. D.
二.填空题
.已知点A是直线上一动点,以点A为顶点的抛物线y=(x﹣m)2+h交y轴于点B,作点B关于x轴的对称点C,连接AB、AC.若△ABC是直角三角形,则点A的坐标为 .
.二次函数y=x2﹣4x+5的对称轴为x= .
.已知y关于x的二次函数y=x2﹣2mx+(m+1)2(m为常数)的顶点坐标为(h,k)
(1)k关于h的函数解析式为 .
(2)若抛物线不经过第三象限,且在﹣2≤x≤2时,二次函数最小值和最大值和为,则m= .
.在平面直角坐标系xOy中,A(﹣2,3),B(1,0),抛物线的解析式为y=ax2+bx+3.
(1)若此抛物线经过A,B两点,则a﹣b= ;
(2)若此抛物线经过点A,且与线段AB有两个不同的交点,则a的取值范围是 .
.点M(m,n)在以y轴为对称轴的二次函数y=﹣x2+bx+2的图象上,则m+n的最大值为 .
三.解答题
.如图,抛物线y=﹣+与x轴交于A、B两点,与y轴交于C点.
(1)求A、B、C三点的坐标;
(2)证明△ABC为直角三角形.
.如图,直线y=﹣x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+x+c经过B,C两点.
(1)求抛物线的解析式;
(2)E是直线BC上方抛物线上的一动点,当点E到直线BC的距离最大时,求点E的坐标;
(3)Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,B,C为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
.在平面直角坐标系中,已知抛物线经过A(﹣2,0),两点,且与y轴交于点C,点B是该抛物线的顶点.
(1)求抛物线L1的表达式;
(2)将L1平移后得到抛物线L2,点D,E在L2上(点D在点E的上方),若以点A,C,D,E为顶点的四边形是正方形,求抛物线L2的解析式.
.已知抛物线y=ax2+c(a≠0)过点P(3,0),Q(1,4).
(1)求抛物线的解析式;
(2)点A在直线PQ上且在第一象限内,过A作AB⊥x轴于B,以AB为斜边在其左侧作等腰直角△ABC.
①若A与Q重合,求C到抛物线对称轴的距离;
②点C能否落在抛物线上,若能求点C的坐标,若不能说明理由.
.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于C点,D为抛物线顶点.连接AD,交y轴于点E,P是抛物线上的一个动点.
(1)如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接EF,AP,若S△ADP=3S△DEF,求点P的坐标.
(2)如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w有最大值还是最小值?w的最值是多少?
参考答案与试题解析
一.选择题
.【解答】解:∵x+y2=3,
∴y2=3﹣x,
∵3﹣x≥0,
∴x≤3,
∴s=x2+8y2=x2+8(3﹣x)=x2﹣8x+24=(x﹣4)2+8,
∴s≥9.
故选:D.
.【解答】解:∵二次函数y=2x2﹣4x﹣1=2(x﹣1)2﹣3,
∴抛物线的对称轴为x=1,顶点(1,﹣3),
∴当y=﹣3时,x=1,
当y=15时,2(x﹣1)2﹣3=15,
解得x=4或x=﹣2,
∵当0≤x≤a时,y的最大值为15,
∴a=4,
故选:D.
.【解答】解:∵y1=y3,x1=0,x3=3,
∴抛物线抛物线对称轴为直线x=﹣=,
∴b=﹣3a,
∵x1<x2<x3,y3>y2,
∴抛物线开口向上,即a>0,
∴b<0,
∴3a+b=0,
故选:A.
.【解答】解:∵y=﹣(x﹣1)2+3,
∴抛物线顶点坐标为(1,3),
故选:B.
.【解答】解:由图象经过(﹣3,0),(1,0)可设抛物线解析式为y=a(x+3)(x﹣1),
将(0,3)代入y=a(x+3)(x﹣1)得3=﹣3a,
解得a=﹣1,
∴y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3=﹣(x+1)2+4,
∴函数最大值为4,b=﹣2.①②正确.
∵抛物线经过(﹣3,0),(1,0),
∴抛物线对称轴为直线x=﹣1,
∵抛物线经过(0,3),
∴抛物线经过(﹣2,3),
∴y≤3时,x≤﹣2或x≥0,③不正确.
当m<4时,方程ax2+bx+c=m有2个不相等的实数根,
∵抛物线关于直线x=﹣1对称,
∴x1+x2=2×(﹣1)=﹣2,④正确.
故选:C.
.【解答】解:∵y=(x+m)2+n,
∴抛物线顶点坐标为(﹣m,n),
∵抛物线顶点在第四象限,
∴m<0,n<0,
∴直线y=mx+n经过第二,三,四象限,
故选:D.
.【解答】解:∵抛物线对称轴为直线x=﹣<0,
∴ab>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc>0.选项A正确.
∵抛物线与x轴有两个不同交点,
∴Δ=b2﹣4ac>0,
∴b2>4ac,选项B正确.
∵抛物线经过(1,0),对称轴为直线x=﹣1,
∴抛物线经过(﹣3,0),
∴﹣3≤x≤1时,y≥0,选项C正确.
∵﹣=﹣1,
∴b=2a,
∵抛物线经过(1,0),
∴a+b+c=3a+c=0,选项D错误.
故选:D.
.【解答】解:∵抛物线经过(﹣5,m),(3,m),
∴抛物线对称轴为直线x=﹣=﹣1,
∴b=2a,y=ax2+2ax+2,
将(1,0)代入y=ax2+2ax+2得0=a+2a+2,
解得a=﹣,
∴y=﹣x2﹣x+2=﹣(x+1)2+,
∴x=﹣1时,y=为函数最大值,
将x=﹣代入y=﹣x2﹣x+2得y=,
将x=0代入代入y=﹣x2﹣x+2得y=2,
∴2<k<满足题意.
故选:C.
.【解答】解:∵一段抛物线y=﹣x2+3x+c(0≤x≤3)与直线y=x+2有唯一公共点,
∴分两种情况:
如图1,抛物线与直线相切,
联立解析式,
∴x2﹣2x+2﹣c=0,
∴Δ=(﹣2)2﹣4(2﹣c)=0,
解得:c=1,
如图2,抛物线与直线相交,且在0≤x≤3上只有一个交点,
此时,两个临界点分别为(0,2),(3,5)在抛物线上,
∴2<c≤5,
∵c为整数,
∴c=3,4,5,
综上所述,c=1,3,4,5,
故选:D.
.【解答】解:∵∠AOB=45°,
∴OA所在直线为y=x,
令x2+n=x,整理得x2﹣x+n=0,
当Δ=1﹣4n=0时,抛物线与线段OA只有1个交点,
解得n=,
当n<时,抛物线向下移动,
当抛物线经过B(2,0)时,0=4+n,
解得n=﹣4,
∴﹣4<n<.
故选:C.
二.填空题
.【解答】解:抛物线y=(x﹣m)2+h的顶点A(m,h),
当x=0时,y=m2+h,
∴A(m,h),B(0,m2+h),
当△ABC是直角三角形时,可能∠BAC=90°或∠ACB=90°,
当∠BAC=90°时,
∵B关于x轴的对称点是C,
∴OB=OC,
∴OA=OB=OC,
∴m2+h2=(m2+h)2①,
∵A在直线y=x上,
∴h=m,代入①得:
m2+m2=,
解得m=0(舍去)或m=﹣或m=,
当m=﹣时,h=﹣1,
当m=时,h=,
∴A(﹣,﹣1)或(,).
当∠ACB=90°时,
yA=yC,
∴m=﹣m2﹣,
∴m=0(舍去)或m=﹣,
∴h=﹣×=﹣,
∴A(﹣,).
故答案为:(﹣,﹣),(﹣,﹣1)或(,).
.【解答】解:∵y=x2﹣4x+5,
∴抛物线对称轴为直线x=﹣=2,
故答案为:2.
.【解答】解:(1)∵y=x2﹣2mx+(m+1)2=(x﹣m)2+2m+1,
∴h=m,k=2m+1,
∴k关于h的函数解析式为k=2h+1,
故答案为:k=2h+1;
(2)令x=0,则y=(m+1)2,
∴抛物线与y轴的交点为(0,(m+1)2).
∵(m+1)2≥0.
∵抛物线不经过第三象限,抛物线的对称轴为直线x=m,
∴m>0.
①当m≥2时,
∵抛物线的开口方向向上,
∴在﹣2≤x≤2时,当x=﹣2时,函数取最大值为y=4+4m+(m+1)2=m2+6m+5,
当x=2时,函数取最小值为y=4﹣4m+(m+1)2=m2﹣2m+5,
∵二次函数最小值和最大值和为,
∴m2+6m+5+m2﹣2m+5=,
即:2m2+4m﹣=0,
解得:m=或(不合题意,舍去),
∴此种情况不存在;
②当0<m<2时,
在﹣2≤x≤2时,当x=﹣2时,函数取最大值为y=4+4m+(m+1)2=m2+6m+5,
当x=m时,函数取最小值为y=2m+1,
∵二次函数最小值和最大值和为,
∴m2+6m+5+2m+1=,
解得:m=或m=﹣(不合题意,舍去),
∴m=.
综上,在﹣2≤x≤2时,二次函数最小值和最大值和为,则m=.
故答案为:.
.【解答】解:(1)将(﹣2,3),(1,0)代入y=ax2+bx+3得,
解得,
∴a﹣b=1.
故答案为:1.
(2)将(﹣2,3)代入y=ax2+bx+3得3=4a﹣2b+3,
∴4a﹣2b=0,
∴b=2a,
∴y=ax2+2ax+3,
∵﹣=﹣1,
∴抛物线对称轴为直线x=﹣1,
将x=﹣1代入y=ax2+2ax+3得y=﹣a+3,
∴抛物线顶点坐标为(﹣1,﹣a+3),
设直线AB解析式为y=kx+b,
将(﹣2,3),(1,0)代入y=kx+b得,
解得,
∴y=﹣x+1,
令ax2+2ax+3=﹣x+1,整理得ax2+(2a+1)x+2=0,
∴Δ=(2a+1)2﹣8a=(2a﹣1)2,
∴a=时,抛物线与直线相切,如图,
当a增大时,抛物线顶点向下移动,抛物线开口变小,符合题意,
∴a>.
当a<0时,抛物线开口向下,
当抛物线经过点B时,由(1)可得a=﹣1,如图,
当a减小时,抛物线顶点向上移动,开口变小,符合题意,
∴a≤﹣1,
故答案为:a>或a≤﹣1.
.【解答】解:∵抛物线y=﹣x2+bx+2的对称轴为y轴,
∴﹣=0,即b=0,
∴y=﹣x2+2,
将(m,n)代入y=﹣x2+2得n=﹣m2+2,
∴m+n=﹣m2﹣m+2=﹣(m+)2+,
∴m=﹣时,m+n最大值为.
故答案为:.
三.解答题
.【解答】(1)解:对于抛物线y=﹣+,当y=0时,则﹣+=0,
解得x1=﹣,x2=2;
当x=0时,y=2,
∴A(﹣,0),B(2,0),C(0,2).
(2)证明:连接AC,BC,
∵OA=,OB=2,∠AOC=∠BOC=90°,
∴AC2=()2+22=6,BC2=(2)2+22=12,
∴AC2+BC2=6+12=18;
∵AB=2﹣(﹣)=3,
∴AB2=(3)2=18,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
.【解答】解:(1)∵直线y=﹣x+4与x轴交于点C,与y轴交于点B,
∴点B,C的坐标分别为B(0,4),C(4,0),
把点B(0,4)和点C(4,0)代入抛物线y=ax2+x+c,
得:,
解之,得,
∴抛物线的解析式为.
(2)∵BC为定值,
∴当△BEC的面积最大时,点E到BC的距离最大.
如图,过点E作EG∥y轴,交直线BC于点G.
设点E的坐标为,则点G的坐标为(m,﹣m+4),
∴,
∴,
∴当m=2时,S△BEC最大,此时点E到BC的距离就最大.此时点E的坐标为(2,4).
(3)存在.由抛物线可得对称轴是直线x=1.
∵Q是抛物线对称轴上的动点,∴点Q的横坐标为1.
①当BC为边时,点B到点C的水平距离是4,
∴点Q到点P的水平距离也是4.
∴点P的横坐标是5或﹣3,∴点P的坐标为或;
②当BC为对角线时,点Q到点C的水平距离是3,
∴点B到点P的水平距离也是3,∴点P的坐标为.
综上所述,在抛物线上存在点P,使得以P,Q,B,C为顶点的四边形是平行四边形,
点P的坐标是或或.
.【解答】解:(1)设抛物线L1的表达式是,
∵抛物线L1过点A(﹣2,0),
∴,
解得,
∴.
即抛物线L1的表达式是;
(2)令x=0,则y=﹣2,∴C(0,﹣2).
Ⅰ.当AC为正方形的对角线时,如图所示,
∵AE3=E3C=CD3=D3A=2,
∴点D3的坐标为(0,0),点E3的坐标为(﹣2,﹣2).
设,则,
解得即抛物线L2的解析式是.
Ⅱ.当AC为边时,分两种情况,
如图,第①种情况,点D1,E1在AC的右上角时.
∵AO=CO=E1O=D1O=2,∴点D1的坐标为(0,2),点E1的坐标为(2,0).
设,
则,
解得:,
即抛物线L2的解析式是.
第②种情况,点D2E2在AC的左下角时,过点D2作D2M⊥x轴,
则有△AD2M≌△AD1O,
∴AO=AM,D1O=D2M.
过E2作E2N⊥y轴,同理可得,△CE2N≌△CE1O,
∴CO=CN,E1O=E2N.
则点D2的坐标为(﹣4,﹣2),点E2的坐标为(﹣2,﹣4),
设,
则,
解得,
即抛物线L2的解析式是.
综上所述:L2的表达式为:,或.
.【解答】解:(1)将P(3,0),Q(1,4)代入y=ax2+c,
∴,
解得,
∴y=﹣x2+;
(2)①∵A与Q重合,
∴A(1,4),
∵AB⊥x轴,
∴AB=4,
∵△ABC是AB为斜边的等腰直角三角形,
∴C点到AB的距离为2,
∵抛物线的对称轴为y轴,
∴C点到抛物线对称轴的距离为1;
②点C能落在抛物线上,理由如下;
设直线PQ的解析式为y=kx+b,
∴,
解得,
∴y=﹣2x+6,
设A(t,﹣2t+6)(0<t<3),
∴AB=﹣2t+6,
∴C点到AB的距离为(﹣2t+6)=﹣t+3,
∴C(2t﹣3,﹣t+3),
将点C代入y=﹣x2+,
可得﹣(2t﹣3)2+=﹣t+3,
解得t=3(舍)或t=,
∴C(﹣2,).
.【解答】解:∵抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于C点,D为抛物线顶点,
∴令x=0,解得y=﹣3,则C(0,﹣3),
令y=0,则x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4),
设直线AD的解析式为y=kx+b(k≠0),
代入A(﹣1,0),D(1,﹣4)得:,
解得,
∴y=﹣2x﹣2,
令x=0,则y=﹣2,
∴E(0,﹣2),
∴,
∴AE=ED,
∴S△FAE=S△FED,
∵S△ADP=3S△DEF,
∴S△APF=S△ADP﹣S△AFD=3S△DEF﹣S△AFD=3S△DEF﹣2S△DEF=S△DEF=S△AEF,
∵OE⊥AF,AF=AF,
∴OE=yp=2,
依题意,设P(m,m2﹣2m﹣3)(m>3),
∴m2﹣2m﹣3=2,
解得(舍),
∴;
(2)∵点P在第四象限的抛物线上,AP、BE交于点G,设P(m,m2﹣2m﹣3)(0<m<3),
设直线AP的解析式为y=cx+d,
代入A(﹣1,0),P(m,m2﹣2m﹣3)得:,
∵0<m<3,
∴m+1≠0,
解得:,
∴直线AP的解析式为y=(m﹣3)x+m﹣3,
设直线BE的解析式为y=k1x+b1,
代入B(3,0),E(0,﹣2)得:,
解得:,
∴直线BE的解析式为,
联立,解得,
∴,
∵0<m<3,
∴m﹣3≠0,
∴=,
令,
∵﹣3<0,
∴z存在最大值,则w存在最小值,
当时,z存在最大值,最大值为,则w的最小值为,
∴w有最小值,w的最小值是.
同课章节目录
