2022-2023学年北师大版九年级数学上册5.2 视图同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册5.2 视图同步练习 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览

文档简介
北师大版九上 5.2 视图
一、选择题(共10小题)
1. 如图是某个几何体的主视图、左视图、俯视图,该几何体是
A. 圆柱 B. 球 C. 圆锥 D. 棱锥
2. 如图是一个由 个相同的正方体组成的立体图形,它的左视图是
A. B.
C. D.
3. 如图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是
A. 5个 B. 6个 C. 7个 D. 8个
4. 一个几何体由大小相同的小方块搭成,从上面看到的如图所示,其中小正方形中的数字表示在该位置的小立方块个数.若允许从该几何体中拿掉部分小立方块,使剩下的几何体从正面和上面看到的形状相同,则拿掉的小立方块数量最多是
A. B. C. D.
5. 一个几何体的三视图如下图所示,该几何体是
A. B.
C. D.
6. 如图(1)所示,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主观图中大矩形边长如图(2)所示,左视图中包含两个全等的矩形,如果用彩色胶带如图(1)包扎礼盒,所需彩色胶带长度至少为
A. B. C. D.
7. 如图,是从三个不同的方向看由一些棱长为 的小正方体构成的立体图形得到的图形,那么这个立体图形的体积是
A. B. C. D.
8. 图是商家用 板制作的“串”字模型,其俯视图是
A. B.
C. D.
9. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是
A. B. C. D.
10. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是
A. B.
C. D.
二、填空题(共6小题)
11. 如图所示的几何体,如果从左面观察它,得到的平面图形是 .
12. 如图,用小木块搭一个几何体,它的主视图和俯视图如图所示.问:最少需要 个小正方体木块,最多需要 个小正方体木块.
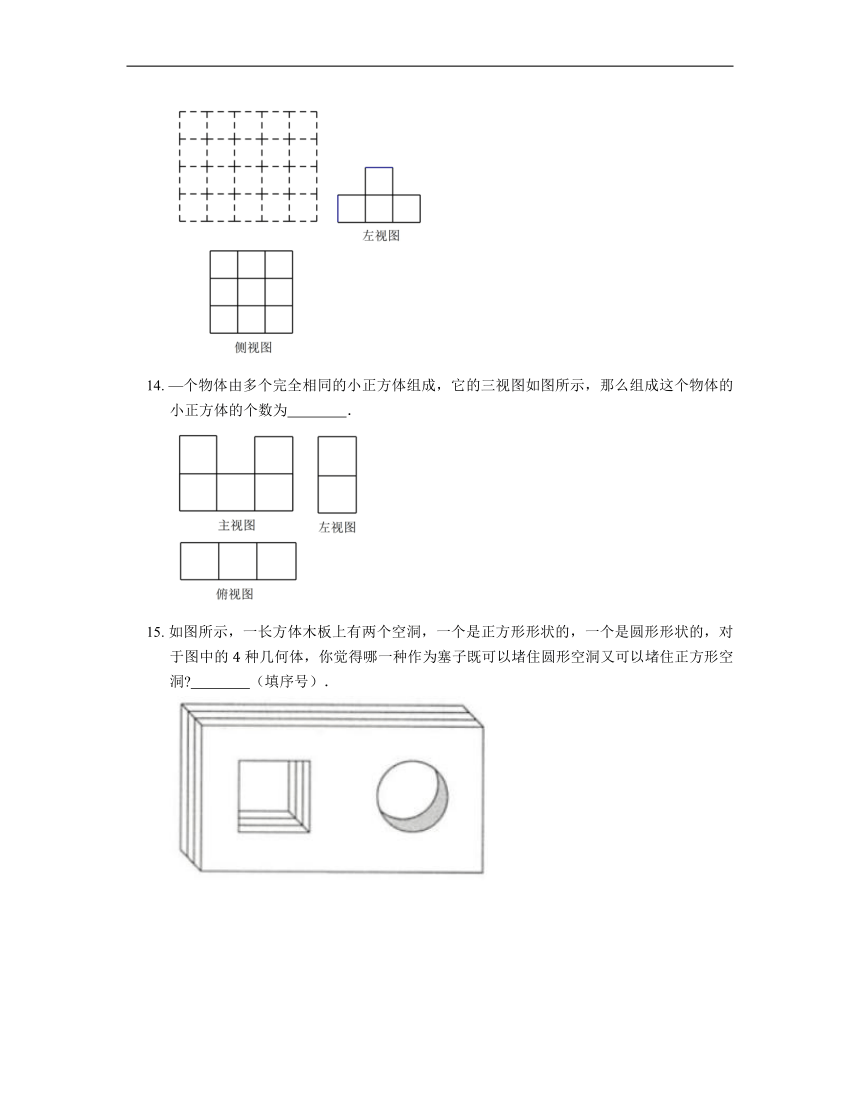
13. 由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
14. —个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为 .
15. 如图所示,一长方体木板上有两个空洞,一个是正方形形状的,一个是圆形形状的,对于图中的 种几何体,你觉得哪一种作为塞子既可以堵住圆形空洞又可以堵住正方形空洞 (填序号).
16. 一个几何体是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,至少需用 块小正方体,最多需用 块小正方体.
三、解答题(共6小题)
17. 如果数学书的每张纸长为 厘米,宽为 厘米,那么该纸张的面积和周长分别是多少
18. 一个缺口朝前的立体图形如图所示,请画出它的三视图.
19. 如图是由一些棱长都为 的小正方体组合成的简单几何体.
(1)画该几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 块小正方体.
20. 由几个相同的棱长为 的小正方体搭成的几何体的俯视图如图()所示,格中的数字表示该位置的小正方体的个数.
(1)请在图()中分别画出这个几何体的主视图和左视图;
(2)根据三视图,求这个组合几何体的表面积.(包括底面积)
(3)若用上述小正方体搭成的几何体的俯视图不变,各位置的小正方体个数可以改变(总数目不变),要使搭成的组合几何体的表面积最大(包括底面积),应该怎么搭,请仿照图(),将数字填写在图()的正方形中.
21. 仓库里有数量足够多的以下四种规格的长方形、正方形的铁片(单位:分米):
从中选 块铁片,焊接成一个无盖的长方体(或正方体)铁盒(忽略材料损耗),甲型盒是由 块规格①, 块规格②和 块规格③的铁片焊接而成的铁盒,乙型盒是容积最小的铁盒.
(1)甲型盒的容积为 立方分米;乙型盒的容积为 立方分米;
(2)现取两个装满水的乙型盒,再将其内部所有的水都倒入一个水平放置的甲型盒,求甲型盒中水的高度.
22. 如图,是一个小正方体所搭几何体从上面看得到的平面图形,正方形中的数字表示在该位置小正方体的个数,请你画出它从正面和左面看得到的平面图形.
答案
1. C
2. C
【解析】左视图为:
3. D
【解析】【分析】结合三视图的知识,主视图以及左视图底面有6个小正方体,共有两层三行,第二层有2个小正方体.
【解析】解:综合主视图,俯视图,左视图底面有6个正方体,第二层有2个正方体,所以搭成这个几何体所用的小立方块的个数是8.
故选:.
【点评】本题考查对三视图的理解应用及空间想象能力.可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的个数.
4. C
【解析】根据题意可得剩下的几何体从正面看的形状(即主视图)如图 所示,
因而左边必须有两层,中间只能是一层,右边最多是两层(至少有一个是两层),因此有如图 所示的三种可能,
最多可拿走 个小立方块.
5. A
【解析】由于俯视图为圆形可得为球、圆柱、圆锥,主视图和左视图为三角形可得此几何体为圆锥.
6. C
【解析】如图所示,画出该礼盒的俯视图,其为正六边形 .连接 ,,
由主视图提供的信息可知 ,易知 为直角三角形,则 ,,所以 ,从而可知该正六边形两对边中点间的线段长为 .又由主视图提供的信息可知,该礼盒的高为 .所以包扎时共用彩色胶带至少为 .
7. A
【解析】观察题图易得,从下往上第一层有 个小正方体,第二层有 个小正方体,一共有 个,故这个立体图形的体积为 .
8. C
【解析】俯视图是从上往下看得到的图形,画视图时,看不见的轮廓线画虚线,看得见的轮廓线画实线
9. D
10. B
【解析】【分析】俯视图有3列,从左到右正方形个数分别是2,1,2.
【解析】解:俯视图从左到右分别是2,1,2个正方形,如图所示:.
故选:.
【点评】本题考查了简单组合体的三视图,培养学生的思考能力和对几何体三种视图的空间想象能力.
11. 三角形
12. ,
13. 如图所示,
14.
15. ②
【解析】图②中圆柱的俯视图是圆,可以堵住圆形空洞,它的主视图和左视图是正方形,可以堵住正方形空洞.
16. ,
17. 平方厘米, 厘米.
18. 根据题意画出图形,如图所示:
19. (1) 三视图如图所示:
(2)
20. (1) 这个几何体的主视图和左视图如图所示:
(2) 由俯视图知,上表面共有 个小正方形,下表面共有 个小正方形;由左视图知,左表面共有 个小正方形,右表面共有 个小正方形;由主视图知,前表面共有 个小正方形,后表面共有 个小正方形.每个小正方形的面积为 ,故这个组合几何体的表面积为 .
(3) (答案不唯一)要使表面积最大,则需满足两个小正方体重合的面最少,此时俯视图如下:
21. (1) ;
【解析】因为甲型盒是由 块规格①, 块规格②和 块规格③的铁片焊接而成的,所以甲型盒的长为 分米,宽为 分米,高为 分米,所以甲型盒的容积为 (立方分米);
乙型盒容积最小,即长、宽、高最小,因此乙型盒为长、宽、高均为 分米的正方体,容积为 (立方分米).
(2) 甲型盒的底面积为 (平方分米),两个乙型盒所盛的水的体积为 (立方分米),
故甲型盒内水的高度为 (分米).
答:甲型盒中水的高度是 分米.
22.
一、选择题(共10小题)
1. 如图是某个几何体的主视图、左视图、俯视图,该几何体是
A. 圆柱 B. 球 C. 圆锥 D. 棱锥
2. 如图是一个由 个相同的正方体组成的立体图形,它的左视图是
A. B.
C. D.
3. 如图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是
A. 5个 B. 6个 C. 7个 D. 8个
4. 一个几何体由大小相同的小方块搭成,从上面看到的如图所示,其中小正方形中的数字表示在该位置的小立方块个数.若允许从该几何体中拿掉部分小立方块,使剩下的几何体从正面和上面看到的形状相同,则拿掉的小立方块数量最多是
A. B. C. D.
5. 一个几何体的三视图如下图所示,该几何体是
A. B.
C. D.
6. 如图(1)所示,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主观图中大矩形边长如图(2)所示,左视图中包含两个全等的矩形,如果用彩色胶带如图(1)包扎礼盒,所需彩色胶带长度至少为
A. B. C. D.
7. 如图,是从三个不同的方向看由一些棱长为 的小正方体构成的立体图形得到的图形,那么这个立体图形的体积是
A. B. C. D.
8. 图是商家用 板制作的“串”字模型,其俯视图是
A. B.
C. D.
9. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是
A. B. C. D.
10. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是
A. B.
C. D.
二、填空题(共6小题)
11. 如图所示的几何体,如果从左面观察它,得到的平面图形是 .
12. 如图,用小木块搭一个几何体,它的主视图和俯视图如图所示.问:最少需要 个小正方体木块,最多需要 个小正方体木块.
13. 由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
14. —个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为 .
15. 如图所示,一长方体木板上有两个空洞,一个是正方形形状的,一个是圆形形状的,对于图中的 种几何体,你觉得哪一种作为塞子既可以堵住圆形空洞又可以堵住正方形空洞 (填序号).
16. 一个几何体是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,至少需用 块小正方体,最多需用 块小正方体.
三、解答题(共6小题)
17. 如果数学书的每张纸长为 厘米,宽为 厘米,那么该纸张的面积和周长分别是多少
18. 一个缺口朝前的立体图形如图所示,请画出它的三视图.
19. 如图是由一些棱长都为 的小正方体组合成的简单几何体.
(1)画该几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 块小正方体.
20. 由几个相同的棱长为 的小正方体搭成的几何体的俯视图如图()所示,格中的数字表示该位置的小正方体的个数.
(1)请在图()中分别画出这个几何体的主视图和左视图;
(2)根据三视图,求这个组合几何体的表面积.(包括底面积)
(3)若用上述小正方体搭成的几何体的俯视图不变,各位置的小正方体个数可以改变(总数目不变),要使搭成的组合几何体的表面积最大(包括底面积),应该怎么搭,请仿照图(),将数字填写在图()的正方形中.
21. 仓库里有数量足够多的以下四种规格的长方形、正方形的铁片(单位:分米):
从中选 块铁片,焊接成一个无盖的长方体(或正方体)铁盒(忽略材料损耗),甲型盒是由 块规格①, 块规格②和 块规格③的铁片焊接而成的铁盒,乙型盒是容积最小的铁盒.
(1)甲型盒的容积为 立方分米;乙型盒的容积为 立方分米;
(2)现取两个装满水的乙型盒,再将其内部所有的水都倒入一个水平放置的甲型盒,求甲型盒中水的高度.
22. 如图,是一个小正方体所搭几何体从上面看得到的平面图形,正方形中的数字表示在该位置小正方体的个数,请你画出它从正面和左面看得到的平面图形.
答案
1. C
2. C
【解析】左视图为:
3. D
【解析】【分析】结合三视图的知识,主视图以及左视图底面有6个小正方体,共有两层三行,第二层有2个小正方体.
【解析】解:综合主视图,俯视图,左视图底面有6个正方体,第二层有2个正方体,所以搭成这个几何体所用的小立方块的个数是8.
故选:.
【点评】本题考查对三视图的理解应用及空间想象能力.可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的个数.
4. C
【解析】根据题意可得剩下的几何体从正面看的形状(即主视图)如图 所示,
因而左边必须有两层,中间只能是一层,右边最多是两层(至少有一个是两层),因此有如图 所示的三种可能,
最多可拿走 个小立方块.
5. A
【解析】由于俯视图为圆形可得为球、圆柱、圆锥,主视图和左视图为三角形可得此几何体为圆锥.
6. C
【解析】如图所示,画出该礼盒的俯视图,其为正六边形 .连接 ,,
由主视图提供的信息可知 ,易知 为直角三角形,则 ,,所以 ,从而可知该正六边形两对边中点间的线段长为 .又由主视图提供的信息可知,该礼盒的高为 .所以包扎时共用彩色胶带至少为 .
7. A
【解析】观察题图易得,从下往上第一层有 个小正方体,第二层有 个小正方体,一共有 个,故这个立体图形的体积为 .
8. C
【解析】俯视图是从上往下看得到的图形,画视图时,看不见的轮廓线画虚线,看得见的轮廓线画实线
9. D
10. B
【解析】【分析】俯视图有3列,从左到右正方形个数分别是2,1,2.
【解析】解:俯视图从左到右分别是2,1,2个正方形,如图所示:.
故选:.
【点评】本题考查了简单组合体的三视图,培养学生的思考能力和对几何体三种视图的空间想象能力.
11. 三角形
12. ,
13. 如图所示,
14.
15. ②
【解析】图②中圆柱的俯视图是圆,可以堵住圆形空洞,它的主视图和左视图是正方形,可以堵住正方形空洞.
16. ,
17. 平方厘米, 厘米.
18. 根据题意画出图形,如图所示:
19. (1) 三视图如图所示:
(2)
20. (1) 这个几何体的主视图和左视图如图所示:
(2) 由俯视图知,上表面共有 个小正方形,下表面共有 个小正方形;由左视图知,左表面共有 个小正方形,右表面共有 个小正方形;由主视图知,前表面共有 个小正方形,后表面共有 个小正方形.每个小正方形的面积为 ,故这个组合几何体的表面积为 .
(3) (答案不唯一)要使表面积最大,则需满足两个小正方体重合的面最少,此时俯视图如下:
21. (1) ;
【解析】因为甲型盒是由 块规格①, 块规格②和 块规格③的铁片焊接而成的,所以甲型盒的长为 分米,宽为 分米,高为 分米,所以甲型盒的容积为 (立方分米);
乙型盒容积最小,即长、宽、高最小,因此乙型盒为长、宽、高均为 分米的正方体,容积为 (立方分米).
(2) 甲型盒的底面积为 (平方分米),两个乙型盒所盛的水的体积为 (立方分米),
故甲型盒内水的高度为 (分米).
答:甲型盒中水的高度是 分米.
22.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
