2022-2023学年人教版九年级数学上册23.1 图形的旋转同步精练(含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册23.1 图形的旋转同步精练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 12:29:55 | ||
图片预览

文档简介
23.1 图形的旋转 同步精练
一、单选题
1.有一个正n边形旋转后与自身重合,则n为( )
A.6 B.9 C.12 D.15
2.在冬奥会开幕式上,美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案本身的设计呈现出充分的美感,它是一个中心对称图形.其实“雪花”图案也可以看成自身的一部分围绕图案的中心依次旋转一定角度得到的,这个角的度数可以是( )
A.30° B.45° C.60° D.90°
3.平面直角坐标系中,为坐标原点,点的坐标为,将绕原点按逆时针方向旋转得,则点的坐标为( )
A. B. C. D.
4.如图,将直角三角板绕顶点A顺时针旋转到,点恰好落在的延长线上,,则为( )
A. B. C. D.
5.将绕点旋转得到,则下列作图正确的是( )
A. B. C. D.
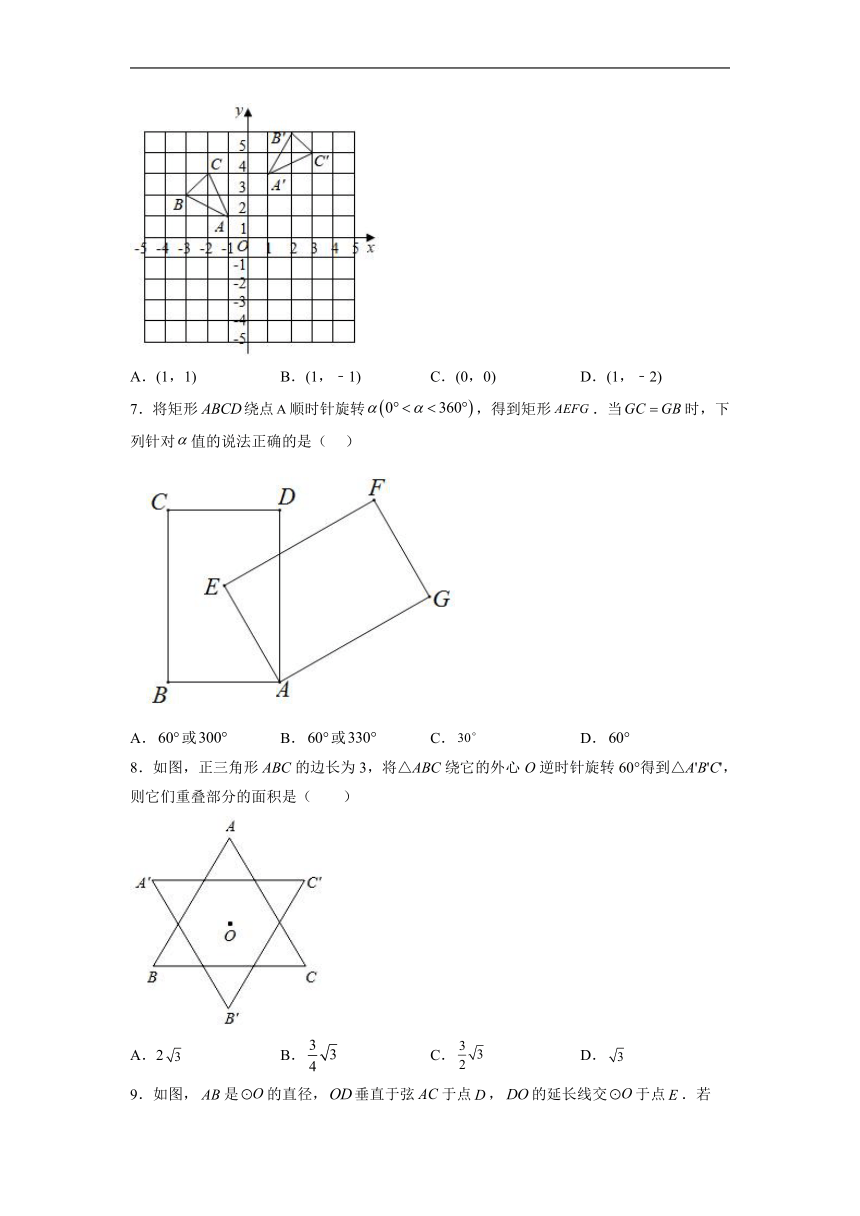
6.如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,旋转得到△A'B'C',则旋转中心的坐标是( )
A.(1,1) B.(1,﹣1) C.(0,0) D.(1,﹣2)
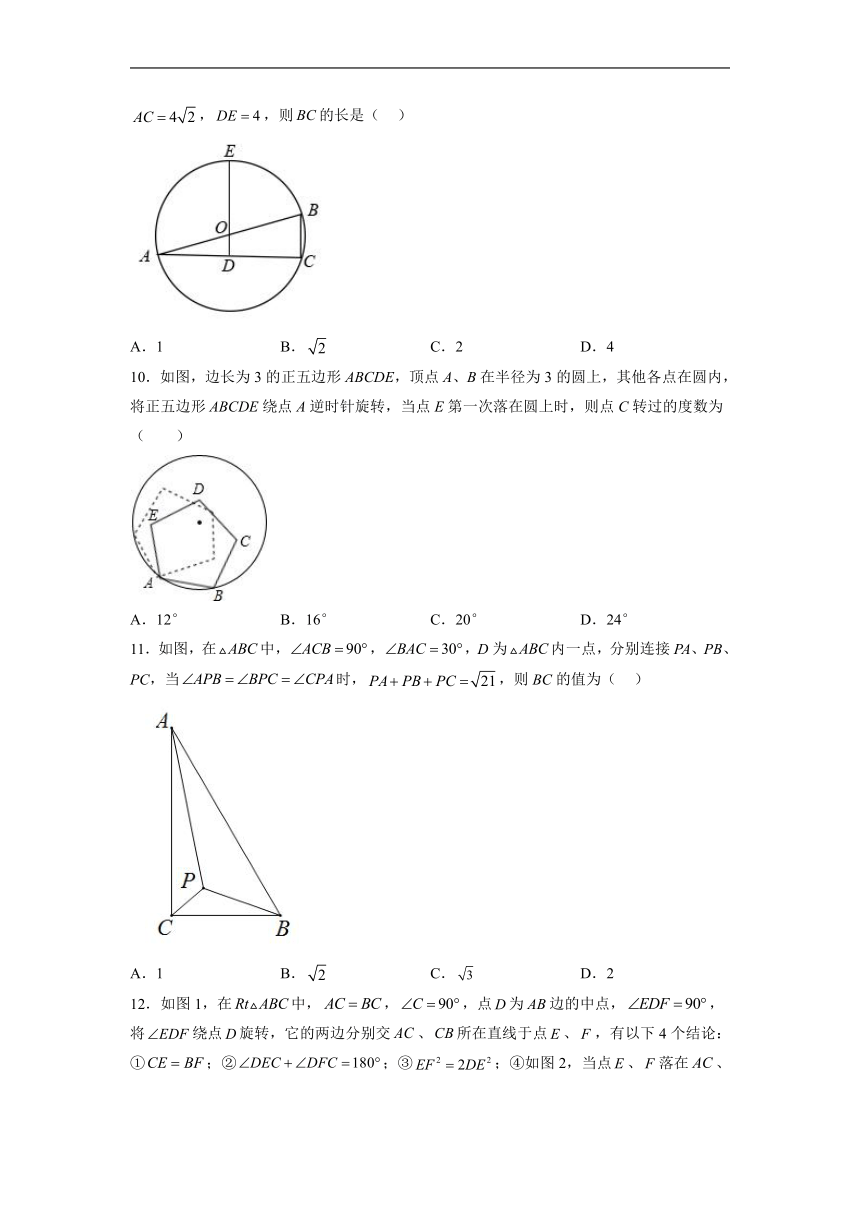
7.将矩形绕点顺时针旋转,得到矩形.当时,下列针对值的说法正确的是( )
A.或 B.或 C. D.
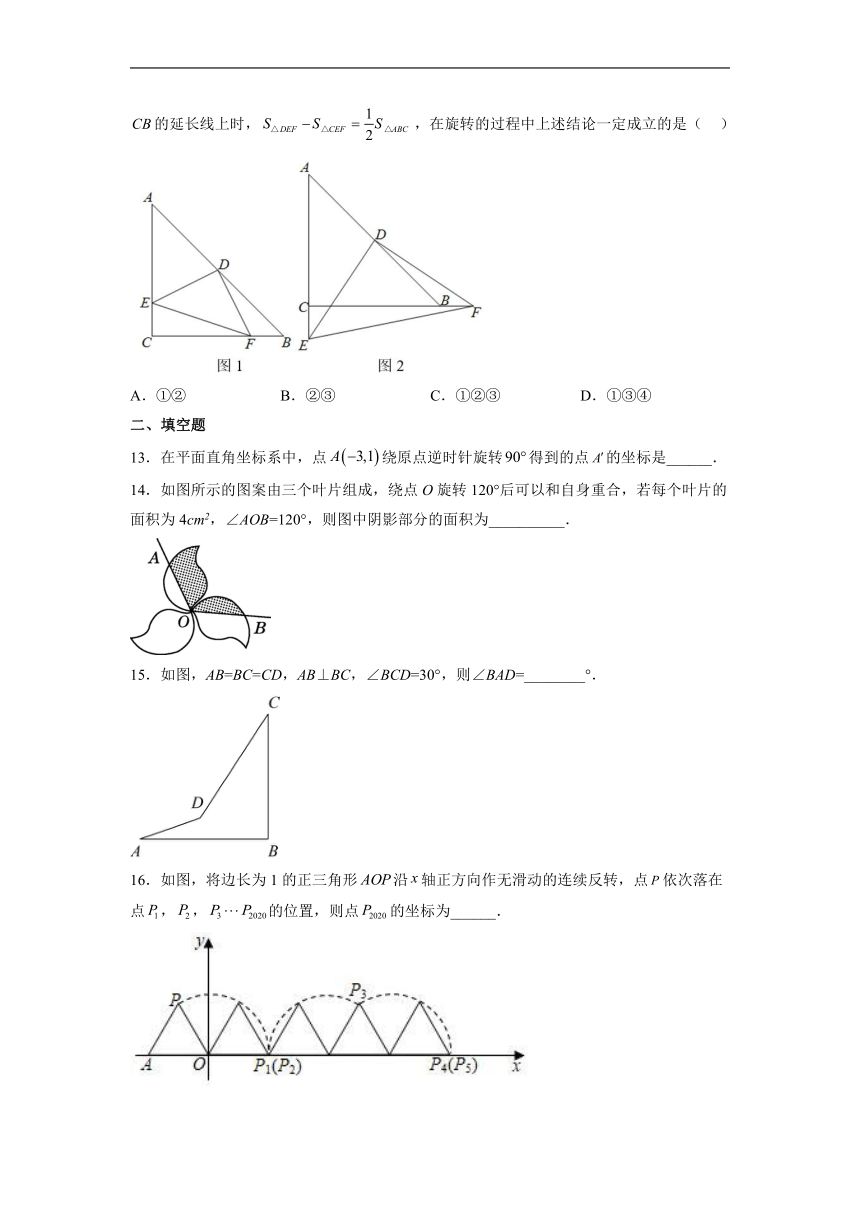
8.如图,正三角形ABC的边长为3,将△ABC绕它的外心O逆时针旋转60°得到△A'B'C',则它们重叠部分的面积是( )
A.2 B. C. D.
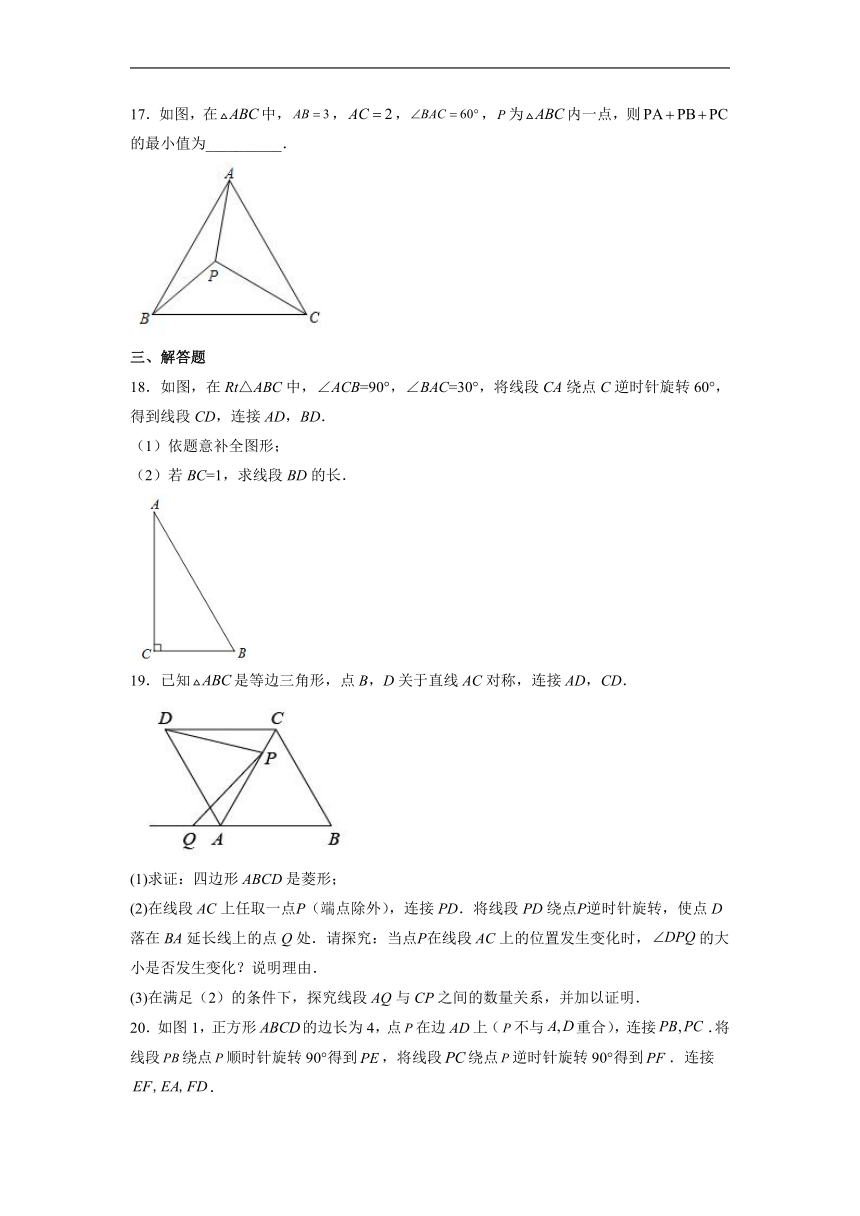
9.如图,是的直径,垂直于弦于点,的延长线交于点.若,,则的长是( )
A.1 B. C.2 D.4
10.如图,边长为3的正五边形ABCDE,顶点A、B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为( )
A.12° B.16° C.20° D.24°
11.如图,在中,,,D为内一点,分别连接PA、PB、PC,当时,,则BC的值为( )
A.1 B. C. D.2
12.如图1,在中,,,点为边的中点,,将绕点旋转,它的两边分别交、所在直线于点、,有以下4个结论:①;②;③;④如图2,当点、落在、的延长线上时,,在旋转的过程中上述结论一定成立的是( )
A.①② B.②③ C.①②③ D.①③④
二、填空题
13.在平面直角坐标系中,点绕原点逆时针旋转得到的点的坐标是______.
14.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2,∠AOB=120°,则图中阴影部分的面积为__________.
15.如图,AB=BC=CD,AB⊥BC,∠BCD=30°,则∠BAD=________°.
16.如图,将边长为1的正三角形沿轴正方向作无滑动的连续反转,点依次落在点,,的位置,则点的坐标为______.
17.如图,在中,,,,为内一点,则的最小值为__________.
三、解答题
18.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,将线段CA绕点C逆时针旋转60°,得到线段CD,连接AD,BD.
(1)依题意补全图形;
(2)若BC=1,求线段BD的长.
19.已知是等边三角形,点B,D关于直线AC对称,连接AD,CD.
(1)求证:四边形ABCD是菱形;
(2)在线段AC上任取一点Р(端点除外),连接PD.将线段PD绕点Р逆时针旋转,使点D落在BA延长线上的点Q处.请探究:当点Р在线段AC上的位置发生变化时,的大小是否发生变化?说明理由.
(3)在满足(2)的条件下,探究线段AQ与CP之间的数量关系,并加以证明.
20.如图1,正方形的边长为4,点在边上(不与重合),连接.将线段绕点顺时针旋转90°得到,将线段绕点逆时针旋转90°得到.连接.
(1)求证:
①的面积;
②;
(2)如图2,的延长线交于点,取的中点,连接,求的取值范围.
21.已知,四边形是正方形,绕点旋转(),,,连接,.
(1)如图,求证:≌;
(2)直线与相交于点.
如图,于点,于点,求证:四边形是正方形;
如图,连接,若,,直接写出在旋转的过程中,线段长度的最小值.
参考答案
1--10CCBBD AACCA 11--12CD
13.(-1,-3)
14.4 cm2
15.15
16.
17.
18.解:(1)根据线段旋转方法,,如图所示即为所求;
(2)∵ ,,,
∴ ,
∴ ,
∵ 线段CA绕点C逆时针旋转60°得到线段CD,
∴且,
∴是等边三角形,
∴ ,,
∴ ,
∴ 在中,
.
19.(1)
连接BD,
是等边三角形,
,
点B,D关于直线AC对称,
AC垂直平分BD,
,
,
四边形ABCD是菱形;
(2)
当点Р在线段AC上的位置发生变化时,的大小不发生变化,始终等于60°,理由如下:
将线段PD绕点Р逆时针旋转,使点D落在BA延长线上的点Q处,
,
是等边三角形,
,
连接PB,过点P作交AB于点E,PF⊥AB于点F,
则,
,
是等边三角形,
,
,
,
点B,D关于直线AC对称,点P在线段AC上,
PB = PD,∠DPA =∠BPA,
PQ = PD,
,
,
∠QPF -∠APF =∠BPF -∠EPF,
即∠QPA = ∠BPE,
∠DPQ =∠DPA - ∠QPA=∠BPA-∠BPE = ∠APE = 60°;
(3)
AQ= CP,证明如下:
AC = AB,AP= AE,
AC - AP = AB – AE,即CP= BE,
AP = EP,PF⊥AB,
AF = FE,
PQ= PD,PF⊥AB,
QF = BF,
QF - AF = BF – EF,即AQ= BE,
AQ= CP.
20.(1)①证明:过点F作FG⊥AD交AD的延长线于点G,
∵∠FPG+∠PFG=90°,∠FPG+∠CPD=90°,
∴∠FPG=∠CPD,
又∵∠PGF=∠CDP=90°,PC=PF,
∴(AAS),
∴FG=PD,
∴的面积;
②过点E作EH⊥DA交DA的延长线于点H,
∵∠EPH+∠PEH=90°,∠EPH +∠BPA=90°,
∴∠PEH =∠BPA,
又∵∠PHE=∠BAP=90°,PB=PE,
∴(AAS),
∴EH=PA,
由①得:FG=PD,
∴EH+FG=PA+PD=AD=CD,
由①得:,
∴PG=CD,
∴PD+GD= CD= EH+FG,
∴FG+ GD= EH+FG,
∴GD=EH,
同理:FG=AH,
又∵∠AHE=∠FGD,
∴,
∴;
(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,
由(1)得:,
∴∠HAE=∠GFD,
∵∠GFD+∠GDF=90°,
∴∠HAE+∠GDF=90°,
∵∠HAE=∠MAD,∠GDF=∠MDA,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∵点N是EF的中点,
∴MN=EF,
∵EH=DG=AP,AH=FG=PD,
∴HG=AH+DG+AD=PD+AP+AD=2AD=8,EH+FG=AP+PD=AD=4,
当点P与点D重合时,FG=0,EH=4,HG=8,
此时EF最大值=,
当点P与AD的中点重合时,FG=2,EH=2,HG=8,
此时EF最小值= HG=8,
∴的取值范围是:4≤MN<.
21(1)证明:四边形是正方形,
,.
,.
,
,
在和中,
≌;
(2)
证明:如图中,设与相交于点.
,
.
≌,
.
,
.
,
,,
四边形是矩形,
.
四边形是正方形,
,.
.
又,
≌.
.
矩形是正方形;
解:作交于点,作于点,
∵
∴≌.
.
,,
最大时,最小,.
.
由可知,是等腰直角三角形,
.
一、单选题
1.有一个正n边形旋转后与自身重合,则n为( )
A.6 B.9 C.12 D.15
2.在冬奥会开幕式上,美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案本身的设计呈现出充分的美感,它是一个中心对称图形.其实“雪花”图案也可以看成自身的一部分围绕图案的中心依次旋转一定角度得到的,这个角的度数可以是( )
A.30° B.45° C.60° D.90°
3.平面直角坐标系中,为坐标原点,点的坐标为,将绕原点按逆时针方向旋转得,则点的坐标为( )
A. B. C. D.
4.如图,将直角三角板绕顶点A顺时针旋转到,点恰好落在的延长线上,,则为( )
A. B. C. D.
5.将绕点旋转得到,则下列作图正确的是( )
A. B. C. D.
6.如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,旋转得到△A'B'C',则旋转中心的坐标是( )
A.(1,1) B.(1,﹣1) C.(0,0) D.(1,﹣2)
7.将矩形绕点顺时针旋转,得到矩形.当时,下列针对值的说法正确的是( )
A.或 B.或 C. D.
8.如图,正三角形ABC的边长为3,将△ABC绕它的外心O逆时针旋转60°得到△A'B'C',则它们重叠部分的面积是( )
A.2 B. C. D.
9.如图,是的直径,垂直于弦于点,的延长线交于点.若,,则的长是( )
A.1 B. C.2 D.4
10.如图,边长为3的正五边形ABCDE,顶点A、B在半径为3的圆上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为( )
A.12° B.16° C.20° D.24°
11.如图,在中,,,D为内一点,分别连接PA、PB、PC,当时,,则BC的值为( )
A.1 B. C. D.2
12.如图1,在中,,,点为边的中点,,将绕点旋转,它的两边分别交、所在直线于点、,有以下4个结论:①;②;③;④如图2,当点、落在、的延长线上时,,在旋转的过程中上述结论一定成立的是( )
A.①② B.②③ C.①②③ D.①③④
二、填空题
13.在平面直角坐标系中,点绕原点逆时针旋转得到的点的坐标是______.
14.如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2,∠AOB=120°,则图中阴影部分的面积为__________.
15.如图,AB=BC=CD,AB⊥BC,∠BCD=30°,则∠BAD=________°.
16.如图,将边长为1的正三角形沿轴正方向作无滑动的连续反转,点依次落在点,,的位置,则点的坐标为______.
17.如图,在中,,,,为内一点,则的最小值为__________.
三、解答题
18.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,将线段CA绕点C逆时针旋转60°,得到线段CD,连接AD,BD.
(1)依题意补全图形;
(2)若BC=1,求线段BD的长.
19.已知是等边三角形,点B,D关于直线AC对称,连接AD,CD.
(1)求证:四边形ABCD是菱形;
(2)在线段AC上任取一点Р(端点除外),连接PD.将线段PD绕点Р逆时针旋转,使点D落在BA延长线上的点Q处.请探究:当点Р在线段AC上的位置发生变化时,的大小是否发生变化?说明理由.
(3)在满足(2)的条件下,探究线段AQ与CP之间的数量关系,并加以证明.
20.如图1,正方形的边长为4,点在边上(不与重合),连接.将线段绕点顺时针旋转90°得到,将线段绕点逆时针旋转90°得到.连接.
(1)求证:
①的面积;
②;
(2)如图2,的延长线交于点,取的中点,连接,求的取值范围.
21.已知,四边形是正方形,绕点旋转(),,,连接,.
(1)如图,求证:≌;
(2)直线与相交于点.
如图,于点,于点,求证:四边形是正方形;
如图,连接,若,,直接写出在旋转的过程中,线段长度的最小值.
参考答案
1--10CCBBD AACCA 11--12CD
13.(-1,-3)
14.4 cm2
15.15
16.
17.
18.解:(1)根据线段旋转方法,,如图所示即为所求;
(2)∵ ,,,
∴ ,
∴ ,
∵ 线段CA绕点C逆时针旋转60°得到线段CD,
∴且,
∴是等边三角形,
∴ ,,
∴ ,
∴ 在中,
.
19.(1)
连接BD,
是等边三角形,
,
点B,D关于直线AC对称,
AC垂直平分BD,
,
,
四边形ABCD是菱形;
(2)
当点Р在线段AC上的位置发生变化时,的大小不发生变化,始终等于60°,理由如下:
将线段PD绕点Р逆时针旋转,使点D落在BA延长线上的点Q处,
,
是等边三角形,
,
连接PB,过点P作交AB于点E,PF⊥AB于点F,
则,
,
是等边三角形,
,
,
,
点B,D关于直线AC对称,点P在线段AC上,
PB = PD,∠DPA =∠BPA,
PQ = PD,
,
,
∠QPF -∠APF =∠BPF -∠EPF,
即∠QPA = ∠BPE,
∠DPQ =∠DPA - ∠QPA=∠BPA-∠BPE = ∠APE = 60°;
(3)
AQ= CP,证明如下:
AC = AB,AP= AE,
AC - AP = AB – AE,即CP= BE,
AP = EP,PF⊥AB,
AF = FE,
PQ= PD,PF⊥AB,
QF = BF,
QF - AF = BF – EF,即AQ= BE,
AQ= CP.
20.(1)①证明:过点F作FG⊥AD交AD的延长线于点G,
∵∠FPG+∠PFG=90°,∠FPG+∠CPD=90°,
∴∠FPG=∠CPD,
又∵∠PGF=∠CDP=90°,PC=PF,
∴(AAS),
∴FG=PD,
∴的面积;
②过点E作EH⊥DA交DA的延长线于点H,
∵∠EPH+∠PEH=90°,∠EPH +∠BPA=90°,
∴∠PEH =∠BPA,
又∵∠PHE=∠BAP=90°,PB=PE,
∴(AAS),
∴EH=PA,
由①得:FG=PD,
∴EH+FG=PA+PD=AD=CD,
由①得:,
∴PG=CD,
∴PD+GD= CD= EH+FG,
∴FG+ GD= EH+FG,
∴GD=EH,
同理:FG=AH,
又∵∠AHE=∠FGD,
∴,
∴;
(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,
由(1)得:,
∴∠HAE=∠GFD,
∵∠GFD+∠GDF=90°,
∴∠HAE+∠GDF=90°,
∵∠HAE=∠MAD,∠GDF=∠MDA,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∵点N是EF的中点,
∴MN=EF,
∵EH=DG=AP,AH=FG=PD,
∴HG=AH+DG+AD=PD+AP+AD=2AD=8,EH+FG=AP+PD=AD=4,
当点P与点D重合时,FG=0,EH=4,HG=8,
此时EF最大值=,
当点P与AD的中点重合时,FG=2,EH=2,HG=8,
此时EF最小值= HG=8,
∴的取值范围是:4≤MN<.
21(1)证明:四边形是正方形,
,.
,.
,
,
在和中,
≌;
(2)
证明:如图中,设与相交于点.
,
.
≌,
.
,
.
,
,,
四边形是矩形,
.
四边形是正方形,
,.
.
又,
≌.
.
矩形是正方形;
解:作交于点,作于点,
∵
∴≌.
.
,,
最大时,最小,.
.
由可知,是等腰直角三角形,
.
同课章节目录
