2022—2023学年人教版数学九年级上册23.1图形的旋转 同步练习 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册23.1图形的旋转 同步练习 (含答案) |

|
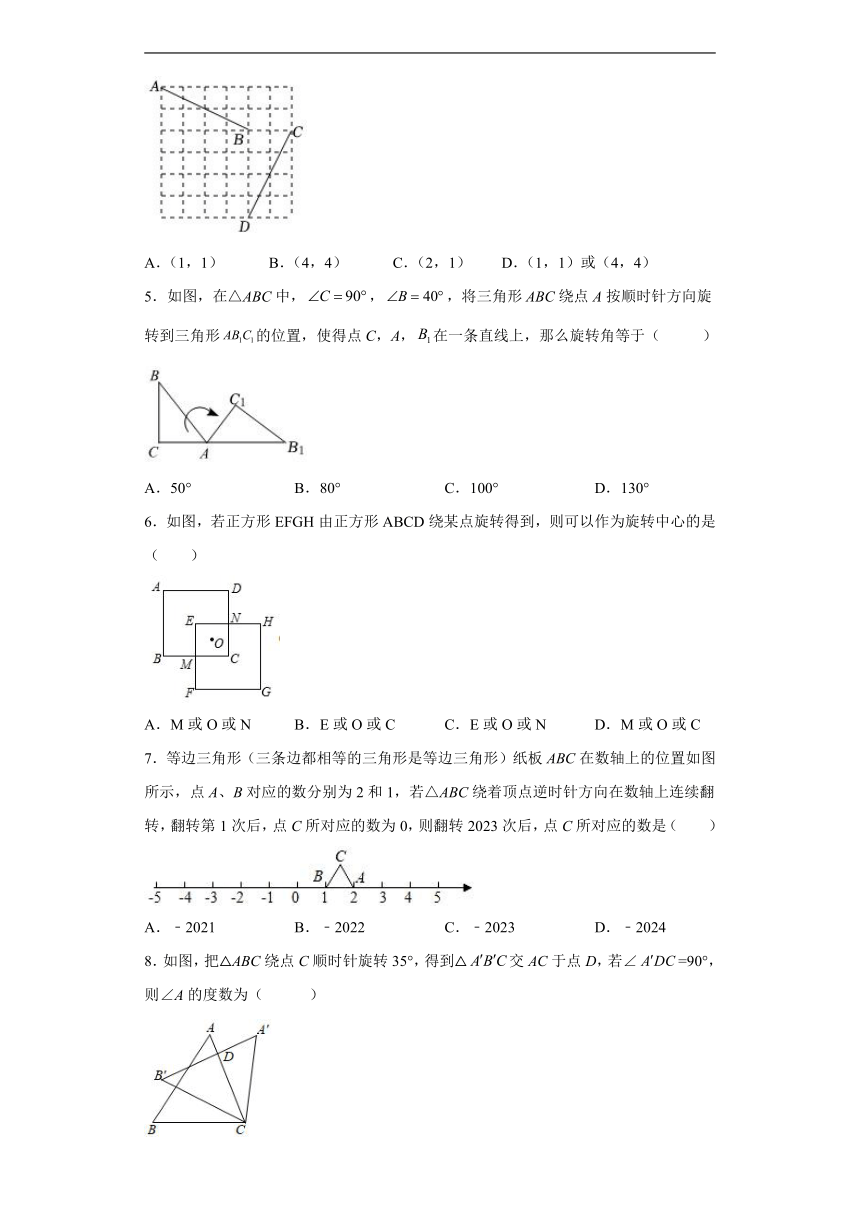
|
| 格式 | docx | ||
| 文件大小 | 629.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 12:32:51 | ||
图片预览



文档简介
23.1 图形的旋转
班级: 姓名: 成绩:
一、选择题
1.北京冬奥会将于2022年2月4日在北京和张家口联合举行,如图是冬奥会的吉祥物“冰墩墩”,将最左边图片按顺时针方向旋转后得到的图片是( )
A. B. C. D.
2.在以下生活现象中,属于旋转变换的是( )
A.钟表的指针和钟摆的运动
B.站在电梯上的人的运动
C.坐在火车上睡觉的旅客
D.地下水位线逐年下降
3.图2是由图1经过某一种图形的运动得到的,这种图形的运动是( )
A.平移 B.翻折 C.旋转 D.以上三种都不对
4.如图,在正方形网格中,线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点,A的对应点是点C),若点A的坐标为(-1,5),点B的坐标为(3,3),则旋转中心O点的坐标为( )
A.(1,1) B.(4,4) C.(2,1) D.(1,1)或(4,4)
5.如图,在△ABC中,,,将三角形ABC绕点A按顺时针方向旋转到三角形的位置,使得点C,A,在一条直线上,那么旋转角等于( )
A.50° B.80° C.100° D.130°
6.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.M或O或N B.E或O或C C.E或O或N D.M或O或C
7.等边三角形(三条边都相等的三角形是等边三角形)纸板ABC在数轴上的位置如图所示,点A、B对应的数分别为2和1,若△ABC绕着顶点逆时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为0,则翻转2023次后,点C所对应的数是( )
A.﹣2021 B.﹣2022 C.﹣2023 D.﹣2024
8.如图,把△ABC绕点C顺时针旋转35°,得到△交AC于点D,若∠=90°,则∠A的度数为( )
A.45° B.55° C.65° D.75°
9.将矩形ABCD绕点B顺时针旋转90°后得到矩形,若AB=12,AD=5,则的面积为( )
A.13 B.26 C.84.5 D.169
10.如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,ADx轴,AD=2,∠A=60°.将菱形ABCD绕点O旋转,使点D落在y轴上,则旋转后点A的对应点的坐标是( ).
A.或 B.
C. D.或
11.如图,在中,.将绕点O逆时针方向旋转,得到,连接,则( )
A.1 B. C. D.
12.已知四边形ABCD中,对角线AC,BD交于点O.将该四边形绕点O旋转180°,恰好能与原四边形重合,则下列结论不一定正确的是( )
A.OA=OC,OB=OD B.AB=CD
C.AC=BD D.∠ABC=∠ADC
13.如图,正方形中,点为对角线的交点,直线过点分别交,于,两点(),若过点作直线与正方形的一组对边分别交于,两点,满足,则这样的直线(不同于直线)的条数共有( )
A.1条 B.2条 C.3条 D.无数条
14.如图,已知菱形ABCD与菱形AEFG全等,菱形AEFG可以看作是菱形ABCD经过怎样的图形变化得到?下列结论:①经过1次平移和1次旋转;②经过1次平移和1次翻折;③经过1次旋转,且平面内可以作为旋转中心的点共有3个.其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
15.如图,是由6×6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,将△ABC绕着边的中点旋转180°,爱观察与思考的小明发现以下结论不正确的是( )
A.△ABC各边的中点都可通过网格确定;
B.△ABC绕着AC的中点旋转180°扫过的面积为13;
C.旋转前后的两个三角形可形成平行四边形;
D.△ABC绕着各边的中点旋转后的△A′B′C′都在网格的格点上.
16.将二次函数y的图象先向下平移2个单位,再把所得图象以原点为中心,旋转180°,所得图象的表达式正确的是( )
A.y=﹣3x2﹣2 B.y=3x2+2 C. D.
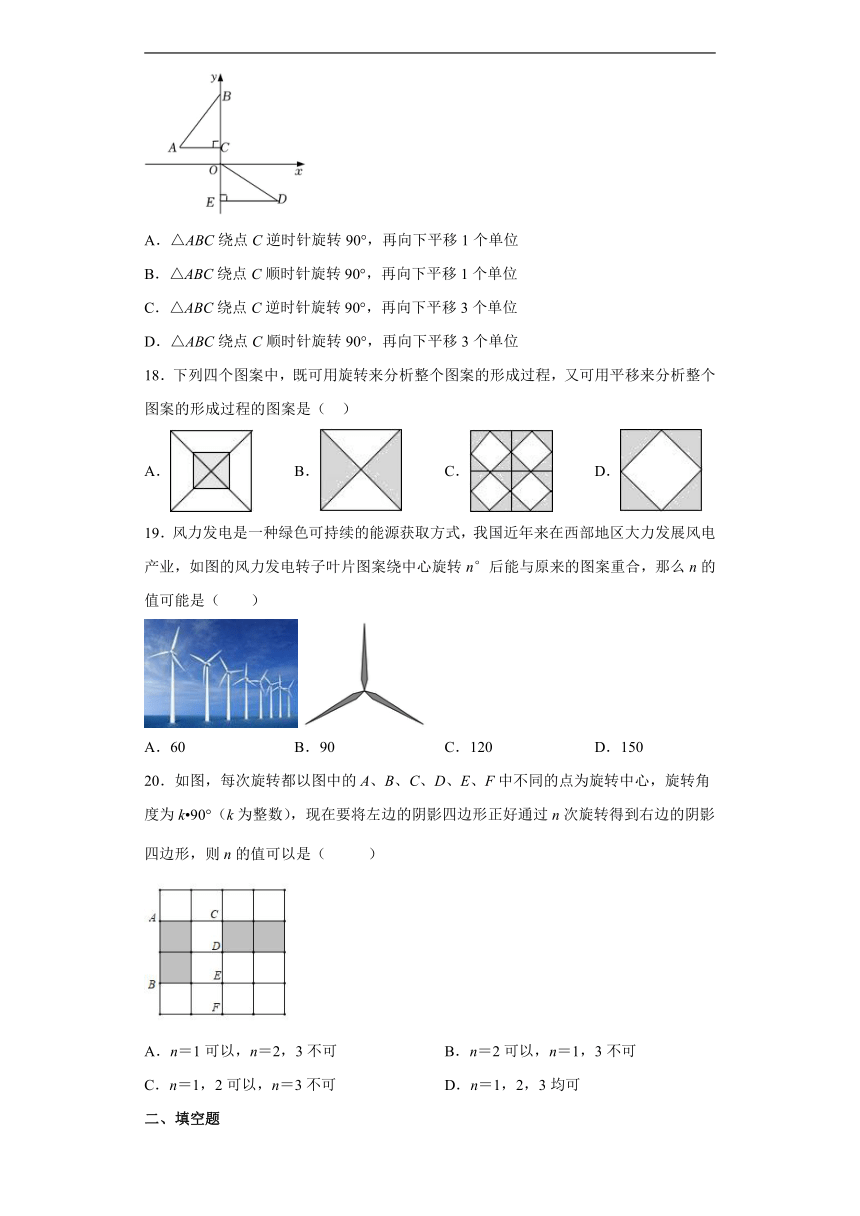
17.如图,在平面直角坐标系中,点B、C、E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )
A.△ABC绕点C逆时针旋转90°,再向下平移1个单位
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位
C.△ABC绕点C逆时针旋转90°,再向下平移3个单位
D.△ABC绕点C顺时针旋转90°,再向下平移3个单位
18.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
A. B. C. D.
19.风力发电是一种绿色可持续的能源获取方式,我国近年来在西部地区大力发展风电产业,如图的风力发电转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A.60 B.90 C.120 D.150
20.如图,每次旋转都以图中的A、B、C、D、E、F中不同的点为旋转中心,旋转角度为k 90°(k为整数),现在要将左边的阴影四边形正好通过n次旋转得到右边的阴影四边形,则n的值可以是( )
A.n=1可以,n=2,3不可 B.n=2可以,n=1,3不可
C.n=1,2可以,n=3不可 D.n=1,2,3均可
二、填空题
21.在冬奥会单板滑雪项目中,运动员的空中姿态优美飘逸.如图,在平面直角坐标系中,将我国运动员的初始位置用△ABC标记,则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置,记为△A′B′C′,在这一过程中,旋转中心的坐标是______.
22.两块全等的等腰直角三角板如图放置,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,当点D落在直线AB上时,若BC=2,则AD=______.
23.将直角边长为1cm的等腰直角三角形ABC绕点A逆时针旋转15°后,得到△,则图中阴影部分的面积是______________.
24.如图,点A坐标为,点B坐标为,点C坐标为,点D坐标为.若线段AB和线段CD间存在某种变换关系,即其中一条线段绕某点旋转一个角度后可以得到另一条线段,则这个旋转中心的坐标是____
25.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转90°得到△CBP′,若PB=3,则PP′的长是______.
三、解答题
26.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的,并写出点的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的
27.已知:如图.△ABC和△DEC都是等边角形.D是BC延长线上一点,AD与BE相交于点P.AC、BE相交于点M,AD、CE相交于点N.
(1)在图①中,求证:AD=BE;
(2)当△CDE绕点C沿逆时针方向旋转到图②时,∠APB= .
28.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,坐标分别为A(2,2),B(1,0),C(3,1).
(1)画出△ABC沿水平方向向左平移4个单位长度的,并直接写出、的坐标;
(2)画出将△ABC绕原点O顺时针旋转所得的,并直接写出、的坐标;
(3)可由绕点G旋转得到,则点G的坐标为 .
29.如图,在正方形中,为边上的一点,将顺时针旋转后得到.
(1)指出旋转中心及旋转的角度;
(2)判断与的位置关系,请说明理由;
(3)如果正方形的面积是,的面积是,求四边形的面积.
试卷第1页,共3页
参考答案
1.D
2.A
3.C
4.A
5.D
6.A
7.B
8.B
9.C
10.A
11.B
12.C
13.C
14.A
15.B
16.D
17.D
18.C
19.C
20.D
21.(2,3)
22.或
23.##
24.或
25.
26.(1)如图,即为所作,点的坐标为(2,-4);
(2)如图,即为所作.
27.(1)证明:∵△ABC和△CDE为等边三角形,
∴AC=BC,CD=CE,∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠DAC=∠EBC,
∵∠AMP=∠BMC,
∴∠APB=∠ACB=60°.
故答案为:60°.
28.解∶(1)如图1,△A1BlC1即为所求作的三角形,由图可知、;
(2)解:如图,△A2B2C2即为所求作的三角形,由图可知、;
(3)解:设G(x0,y0),
∵可由绕点G旋转得到,、,、,
∴,
化简得,
解得,
∴G(-2,-2),
故答案为:G(-2,-2).
29.(1)解:根据题意知:旋转中心是B,旋转角是90°;
(2)延长AE交CF于点M.
∵△ABE≌△CBF,
∴∠EAB=∠BCF.
又∵∠AEB=∠CEM,∠ABE=90°,
∴∠ECM+∠CEM=90°,
∴AE⊥CF.
(3)∵△ABE≌△CBF,的面积是
∴△ABE的面积是,
又∵正方形的面积是
∴四边形AECD的面积是18-2=.
班级: 姓名: 成绩:
一、选择题
1.北京冬奥会将于2022年2月4日在北京和张家口联合举行,如图是冬奥会的吉祥物“冰墩墩”,将最左边图片按顺时针方向旋转后得到的图片是( )
A. B. C. D.
2.在以下生活现象中,属于旋转变换的是( )
A.钟表的指针和钟摆的运动
B.站在电梯上的人的运动
C.坐在火车上睡觉的旅客
D.地下水位线逐年下降
3.图2是由图1经过某一种图形的运动得到的,这种图形的运动是( )
A.平移 B.翻折 C.旋转 D.以上三种都不对
4.如图,在正方形网格中,线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点,A的对应点是点C),若点A的坐标为(-1,5),点B的坐标为(3,3),则旋转中心O点的坐标为( )
A.(1,1) B.(4,4) C.(2,1) D.(1,1)或(4,4)
5.如图,在△ABC中,,,将三角形ABC绕点A按顺时针方向旋转到三角形的位置,使得点C,A,在一条直线上,那么旋转角等于( )
A.50° B.80° C.100° D.130°
6.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.M或O或N B.E或O或C C.E或O或N D.M或O或C
7.等边三角形(三条边都相等的三角形是等边三角形)纸板ABC在数轴上的位置如图所示,点A、B对应的数分别为2和1,若△ABC绕着顶点逆时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为0,则翻转2023次后,点C所对应的数是( )
A.﹣2021 B.﹣2022 C.﹣2023 D.﹣2024
8.如图,把△ABC绕点C顺时针旋转35°,得到△交AC于点D,若∠=90°,则∠A的度数为( )
A.45° B.55° C.65° D.75°
9.将矩形ABCD绕点B顺时针旋转90°后得到矩形,若AB=12,AD=5,则的面积为( )
A.13 B.26 C.84.5 D.169
10.如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,ADx轴,AD=2,∠A=60°.将菱形ABCD绕点O旋转,使点D落在y轴上,则旋转后点A的对应点的坐标是( ).
A.或 B.
C. D.或
11.如图,在中,.将绕点O逆时针方向旋转,得到,连接,则( )
A.1 B. C. D.
12.已知四边形ABCD中,对角线AC,BD交于点O.将该四边形绕点O旋转180°,恰好能与原四边形重合,则下列结论不一定正确的是( )
A.OA=OC,OB=OD B.AB=CD
C.AC=BD D.∠ABC=∠ADC
13.如图,正方形中,点为对角线的交点,直线过点分别交,于,两点(),若过点作直线与正方形的一组对边分别交于,两点,满足,则这样的直线(不同于直线)的条数共有( )
A.1条 B.2条 C.3条 D.无数条
14.如图,已知菱形ABCD与菱形AEFG全等,菱形AEFG可以看作是菱形ABCD经过怎样的图形变化得到?下列结论:①经过1次平移和1次旋转;②经过1次平移和1次翻折;③经过1次旋转,且平面内可以作为旋转中心的点共有3个.其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
15.如图,是由6×6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,将△ABC绕着边的中点旋转180°,爱观察与思考的小明发现以下结论不正确的是( )
A.△ABC各边的中点都可通过网格确定;
B.△ABC绕着AC的中点旋转180°扫过的面积为13;
C.旋转前后的两个三角形可形成平行四边形;
D.△ABC绕着各边的中点旋转后的△A′B′C′都在网格的格点上.
16.将二次函数y的图象先向下平移2个单位,再把所得图象以原点为中心,旋转180°,所得图象的表达式正确的是( )
A.y=﹣3x2﹣2 B.y=3x2+2 C. D.
17.如图,在平面直角坐标系中,点B、C、E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )
A.△ABC绕点C逆时针旋转90°,再向下平移1个单位
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位
C.△ABC绕点C逆时针旋转90°,再向下平移3个单位
D.△ABC绕点C顺时针旋转90°,再向下平移3个单位
18.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是( )
A. B. C. D.
19.风力发电是一种绿色可持续的能源获取方式,我国近年来在西部地区大力发展风电产业,如图的风力发电转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A.60 B.90 C.120 D.150
20.如图,每次旋转都以图中的A、B、C、D、E、F中不同的点为旋转中心,旋转角度为k 90°(k为整数),现在要将左边的阴影四边形正好通过n次旋转得到右边的阴影四边形,则n的值可以是( )
A.n=1可以,n=2,3不可 B.n=2可以,n=1,3不可
C.n=1,2可以,n=3不可 D.n=1,2,3均可
二、填空题
21.在冬奥会单板滑雪项目中,运动员的空中姿态优美飘逸.如图,在平面直角坐标系中,将我国运动员的初始位置用△ABC标记,则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置,记为△A′B′C′,在这一过程中,旋转中心的坐标是______.
22.两块全等的等腰直角三角板如图放置,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,当点D落在直线AB上时,若BC=2,则AD=______.
23.将直角边长为1cm的等腰直角三角形ABC绕点A逆时针旋转15°后,得到△,则图中阴影部分的面积是______________.
24.如图,点A坐标为,点B坐标为,点C坐标为,点D坐标为.若线段AB和线段CD间存在某种变换关系,即其中一条线段绕某点旋转一个角度后可以得到另一条线段,则这个旋转中心的坐标是____
25.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转90°得到△CBP′,若PB=3,则PP′的长是______.
三、解答题
26.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的,并写出点的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的
27.已知:如图.△ABC和△DEC都是等边角形.D是BC延长线上一点,AD与BE相交于点P.AC、BE相交于点M,AD、CE相交于点N.
(1)在图①中,求证:AD=BE;
(2)当△CDE绕点C沿逆时针方向旋转到图②时,∠APB= .
28.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,坐标分别为A(2,2),B(1,0),C(3,1).
(1)画出△ABC沿水平方向向左平移4个单位长度的,并直接写出、的坐标;
(2)画出将△ABC绕原点O顺时针旋转所得的,并直接写出、的坐标;
(3)可由绕点G旋转得到,则点G的坐标为 .
29.如图,在正方形中,为边上的一点,将顺时针旋转后得到.
(1)指出旋转中心及旋转的角度;
(2)判断与的位置关系,请说明理由;
(3)如果正方形的面积是,的面积是,求四边形的面积.
试卷第1页,共3页
参考答案
1.D
2.A
3.C
4.A
5.D
6.A
7.B
8.B
9.C
10.A
11.B
12.C
13.C
14.A
15.B
16.D
17.D
18.C
19.C
20.D
21.(2,3)
22.或
23.##
24.或
25.
26.(1)如图,即为所作,点的坐标为(2,-4);
(2)如图,即为所作.
27.(1)证明:∵△ABC和△CDE为等边三角形,
∴AC=BC,CD=CE,∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠DAC=∠EBC,
∵∠AMP=∠BMC,
∴∠APB=∠ACB=60°.
故答案为:60°.
28.解∶(1)如图1,△A1BlC1即为所求作的三角形,由图可知、;
(2)解:如图,△A2B2C2即为所求作的三角形,由图可知、;
(3)解:设G(x0,y0),
∵可由绕点G旋转得到,、,、,
∴,
化简得,
解得,
∴G(-2,-2),
故答案为:G(-2,-2).
29.(1)解:根据题意知:旋转中心是B,旋转角是90°;
(2)延长AE交CF于点M.
∵△ABE≌△CBF,
∴∠EAB=∠BCF.
又∵∠AEB=∠CEM,∠ABE=90°,
∴∠ECM+∠CEM=90°,
∴AE⊥CF.
(3)∵△ABE≌△CBF,的面积是
∴△ABE的面积是,
又∵正方形的面积是
∴四边形AECD的面积是18-2=.
同课章节目录
