2022-2023学年鲁教版数学九年级上册第一章 反比例函数 题型分类综合练习题 (含答案)
文档属性
| 名称 | 2022-2023学年鲁教版数学九年级上册第一章 反比例函数 题型分类综合练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 12:11:13 | ||
图片预览



文档简介
2022-2023学年鲁教版九年级数学上册《第1章反比例函数》题型分类综合练习题(附答案)
一.反比例函数的图象
1.已知y=(m+1)xm+2是反比例函数,则函数的图象在( )
A.第一、二象限 B.第二、四象限
C.第一、三象限 D.第三、四象限
2.函数y=﹣的大致图象是( )
A.B.C.D.
3.如果矩形面积为6cm2,那么它的长ycm与宽xcm之间函数关系用图象表示大致是( )
A.B.C.D.
二.反比例函数的性质
4.下列函数y=﹣8x,y=5x﹣1,y=,y=(x>0),y=﹣(x<0)中,y随x的增大而减小的( )
A.4个 B.3个 C.2个 D.1个
5.已知反比例函数y=,下列结论中不正确的是( )
A.其图像经过点(﹣1,﹣3) B.其图像分别位于第一、第三象限
C.当x<0时,y随x的增大而增大 D.当x>1时,0<y<3
6.如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
﹣1 B.﹣2
C.﹣3 D.﹣4
三.反比例函数系数k的几何意义
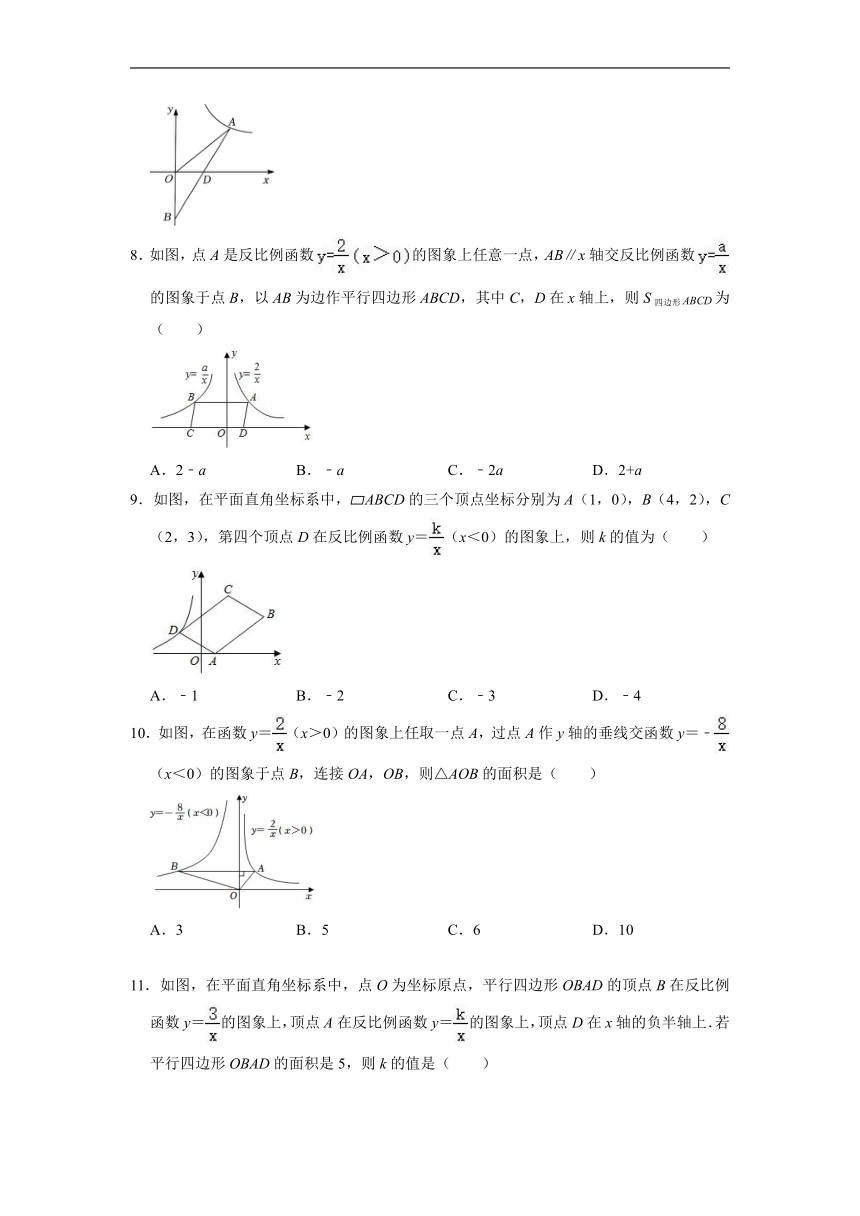
7.如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图象经过点A,若S△OAB=1,则k的值为 .
8.如图,点A是反比例函数的图象上任意一点,AB∥x轴交反比例函数的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,则S四边形ABCD为( )
A.2﹣a B.﹣a C.﹣2a D.2+a
9.如图,在平面直角坐标系中, ABCD的三个顶点坐标分别为A(1,0),B(4,2),C(2,3),第四个顶点D在反比例函数y=(x<0)的图象上,则k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
10.如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
11.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A.2 B.1 C.﹣1 D.﹣2
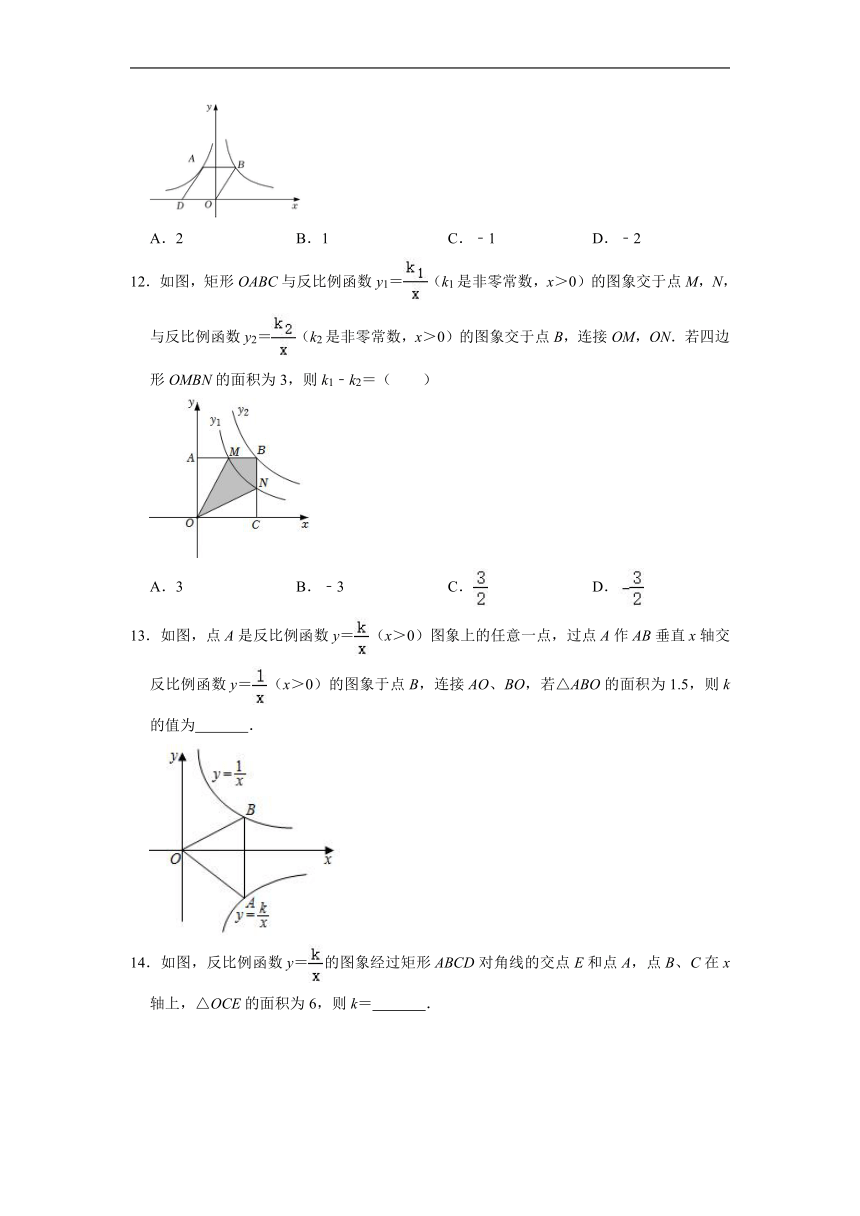
12.如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )
A.3 B.﹣3 C. D.
13.如图,点A是反比例函数y=(x>0)图象上的任意一点,过点A作AB垂直x轴交反比例函数y=(x>0)的图象于点B,连接AO、BO,若△ABO的面积为1.5,则k的值为 .
14.如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k= .
15.如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .
16.如图,点A、B在反比例函数的图象上,AC⊥y轴,垂足为D,BC⊥AC.若四边形AOBC的面积为6,,则k的值为 .
四.反比例函数图象上点的坐标特征
17.在反比例函数(k为常数)上有三点A(x1,y1),B(x2,y2),C(x3,y3),若x1<0<x2<x3,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y2<y1
18.已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
19.如图,等边△ABC的顶点A,B分别在函数y=﹣图象的两个分支上,且AB经过原点O.当点A在函数y=﹣的图象上移动时,顶点C始终在函数y=的图象上移动,则k的值为( )
A.6 B.9 C.2 D.3
20.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(k>0,x>0)的图象上,点D的坐标为(4,3)则k的值为( )
A.32 B.24 C.20 D.12
21.如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则k的值为( )
A.4 B.﹣4 C.﹣3 D.3
22.正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
五.待定系数法求反比例函数解析式
23.如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则经过点B的反比例函数的解析式为 .
六.反比例函数与一次函数的交点问题
24.如图,正比例函数y=kx与反比例函数y=的图象交于A,B两点,BC∥x轴,AC∥y轴,则S△ABC=( )
A.10 B.11 C.12 D.13
25.如图,一次函数y1=k1x+b与反比例函数y2=的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式k1x+b<的解集是( )
A.﹣1<x<0或x>2 B.x<﹣1或0<x<2
C.x<﹣1或x>2 D.﹣1<x<2
26.如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A.x<﹣2或x>2 B.﹣2<x<2
C.﹣2<x<0或x>2 D.x<﹣2或0<x<2
27.如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
28.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=和y=的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
29.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1),点B的坐标为(﹣1,m).
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积.
30.如图一次函数y=kx+b的图象与反比例函数的图象交于点A(2,5)和点B(n,2).
(1)求m,n的值;
(2)连接OA,OB,求△OAB的面积.
31.如图,一次函数y1=x+b的图象与反比例函数y2=的图象相交于点A(2,3)和B两点,点B的横坐标是﹣3.
(1)求一次函数和反比例函数的解析式;
(2)直接写出y1≤y2时,x的取值范围;
(3)求△AOB的面积.
32.如图,已知点A(4,m)、B(n,﹣4)是一次函数y=x+n的图象与反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)求点O到直线AB的距离;
(4)请直接写出关于x的不等式x+n>的解集: .
33.如图,平面直角坐标系中,直线y1=kx+b(k、b为常数,k≠0)分别与x,y轴相交于点A,B,与双曲线y2=(m为常数,m≠0)分别交于点C,D(点C在第一象限,点D在第三象限),作CE⊥x轴于点E.已知OA=8,OE=OB=4.
(1)求直线y1和双曲线y2的解析式;
(2)在y轴上是否存在一点P,使S△ABP=S△CEO?若存在,请求出P的坐标:若不存在,请说明理由.
34.已知函数y1=ax+1﹣k,y2=,其中a,k都为常数,且ak≠0.y2的图象经过点(1,2).
(1)若y1的图象也经过点(1,2).
①求这两个函数的解析式.
②当y1>y2时,求x的取值范围.
(2)直线x=m分别交函数y1和y2的图象于点A(xA,yA),B(xB,yB),且点B到x轴的距离为2,若yA﹣yB=2,求a的值.
35.如图,一次函数y=k1x的图象与反比例函数y=(x>0)的图象交于点C(6,),且横坐标为1的点P也在反比例函数y=(x>0)的图象上,另有一直线l经过点P,C.
(1)k1= ,k2= .
(2)求直线l的函数表达式;
(3)设直线l与y轴交于点A,将直线OC沿射线CP方向平移至点A处停止,请求出直线OC在平移过程中与x轴交点的横坐标的取值范围.
36.如图,一次函数y=k1x+b(k1≠0)与反比例函数y=(k2≠0)的图象交于点A(﹣4,﹣1)和点B(a,3).
(1)求反比例函数和一次函数的关系式;
(2)求△OAB的面积;
(3)P是直线AB下方反比例函数图象上一点,且△PAB的面积与△OAB的面积相等,求点P的坐标.
七.反比例函数与一次函数的交点问题
37.如图,已知反比例函数为常数)的图象与一次函数y=ax+b的图象交于A(1,3),B(m,1)两点.
(1)求反比例函数及一次函数的表达式;
(2)已知点P(n,0),过点P作平行于y轴的直线,交一次函数图象于点M,且点M在第一象限内,交反比例函数图象于点N.若点P到点M的距离小于线段PN的长度,结合函数图象直接写出n的取值范围.
八.反比例函数综合题
38.如图1,一次函数y1=x+2与反比例函数交于A,B两点,点A的横坐标为﹣3.
(1)求出反比例函数的表达式及点B的坐标;
(2)当y1<y2时,直接写出x的取值范围;
(3)如图2,在第二象限中存在一点P,使得四边形PAOB是菱形,求菱形PAOB的面积.
39.如图,反比例函数y1=(k≠0)的图象与正比例函数y2=﹣x的图象相交于A(a,3)B两点.
(1)求k的值及B点的坐标;
(2)直接写出不等式x的解集;
(3)已知AD∥x轴,以AB、AD为边作菱形ABCD,求菱形ABCD的面积.
40.已知:如图1,点A(4,n)是反比例函数y=(x>0)图象上的一点.
(1)求n的值和直线OA的解析式;
(2)如图2,将反比例函数y=(x>0)的图象绕原点O逆时针旋转45°后,与y轴交于点M,求线段OM的长度;
(3)如图3,将直线OA绕原点O逆时针旋转45°,与反比例函数y=(x>0)的图象交于点B,求点B的坐标.
参考答案
一.反比例函数的图象
1.解:依题意有m+2=﹣1,
解得m=﹣3,
因而函数是y=,
故函数经过第二、四象限.
故选:B.
2.解:因为k=﹣2,y=﹣<0,所以它的两个分支分别位于第三、四象限.
故选:D.
3.解:由矩形的面积公式可得xy=6,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
二.反比例函数的性质
4.解:∵y=﹣8x中,k=﹣8<0,
∴y随x增大而减小;
∵y=5x﹣1中,k=5>0,
∴y随x增大而增大;
∵y=中,k=6>0,
∴在一、三象限内,y随x增大而减小.
∵y=(x>0),
∴当x>0,y随x增大而减小,
∵y=﹣(x<0)中,k=﹣1<0,
∴当x<0,y随x增大而增大;
故选:C.
5.解:将(﹣1,﹣3)代入解析式,得﹣3=﹣3,故A正确,不符合题意;
由于k=3>0,则函数图象过一、三象限,在每个象限内,y随x的增大而减小,故B正确,不符合题意、C错误,符合题意;
∵x=1时,y=3,且当x>0时y随x的增大而减小
∴当x>1时,0<y<3,故D正确,不符合题意,
故选:C.
6.解:∵点E为OC的中点,
∴△AEO的面积=△AEC的面积=,
∵点A,C为函数y=(x<0)图象上的两点,
∴S△ABO=S△CDO,
∴S四边形CDBE=S△AEO=,
∵EB∥CD,
∴△OEB∽△OCD,
∴=()2,
∴S△OCD=1,
则xy=﹣1,
∴k=xy=﹣2.
故选:B.
三.反比例函数系数k的几何意义
7.解:设A(a,b),如图,作A 过x轴的垂线与x 轴交于C,
则:AC=b,OC=a,AC∥OB,
∴∠ACD=∠BOD=90°,∠ADC=∠BDO,
∵BD=AD,
∴△ADC≌△BDO(AAS),
∴S△ADC=S△BDO,
∴S△OAC=S△AOD+S△ADC=S△AOD+S△BDO=S△AOB=1,
∴×OC×AC=ab=1,
∴ab=2,
∵A(a,b) 在y=上,
∴k=ab=2.
故答案为:2.
8.解:连接OA、OB,AB交y轴于E,如图,
∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA==1,S△OBE=|a|=﹣a,
∴S△OAB=1﹣a,
∵四边形ABCD为平行四边形,
∴S四边形ABCD=2S△OAB=2﹣a.
故选:A.
9.解:过点D作DE⊥x轴于点E,CF⊥x轴于F,作BH∥x轴,交CF于H,
∵A(1,0),B(4,2),C(2,3),
∴BH=4﹣2=2,CH=3﹣2=1,
∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∴∠DAB+∠ABC=180°,
∵BH∥x轴,
∴∠ABH=∠BAF,
∵∠DAE+∠BAF+∠DAB=180°=∠CBH+∠ABH+∠DAB,
∴∠DAE=∠CBH,
在△ADE和△BCH中,
,
∴△ADE≌△BCH(AAS),
∴AE=BH=2,DE=CH=1,
∴OE=1,
∴点D坐标为(﹣1,1),
∵点D在反比例函数y=(x<0)的图象上,
∴k=﹣1×1=﹣1,
故选:A.
10.解:∵点A在函数y=(x>0)的图象上,
∴S△AOC=×2=1,
又∵点B在反比例函数y=﹣(x<0)的图象上,
∴S△BOC=×8=4,
∴S△AOB=S△AOC+S△BOC
=1+4
=5,
故选:B.
11.解:设B(a,),
∵四边形OBAD是平行四边形,
∴AB∥DO,
∴A(,),
∴AB=a﹣,
∵平行四边形OBAD的面积是5,
∴(a﹣)=5,
解得k=﹣2,
故选:D.
12.解:∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,
∴S△OAM=S△OCN=k1,
∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,
∴S矩形OABC=k2,
∴S矩形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,
∴k2﹣k1=3,
∴k1﹣k2=﹣3,
故选:B.
13.解:设AB与x轴交于点C,
点B在反比例函数y=的图象上,
∴S△BOC=|k|=,
又∵S△AOB=1.5,
∴S△AOC=1.5﹣=1=|k|,
又∵k<0,
∴k=﹣2,
故答案为:﹣2.
14.解:如图,过点E作EH⊥BC于H,
设点A(a,),C(c,0),
∵点E是矩形ABCD的对角线的交点,
∴E(,),
∵点E在反比例函数y=的图象上,
∴=k,
∴c=3a,
∵△OCE的面积为6,
∴OC EH=c =×3a =6,
∴k=8,
故答案为:8.
15.解:因为D为AC的中点,△AOD的面积为3,
所以△AOC的面积为6,
所以k=12=2m.
解得:m=6.
故答案为:6.
16.解:设点,
∵AC⊥y轴,
∴AD=a,,
∵,
∴AC=2a,
∴CD=3a,
∵BC⊥AC.AC⊥y轴,
∴BC∥y轴,
∴点B,
∴,
∵S梯形OBCD=S△AOD+S四边形AOBC,
∴,
解得:k=3.
故答案为:3.
四.反比例函数图象上点的坐标特征
17.解:∵k2≥0,
∴k2+3>0.
∴反比例函数(k为常数)的函数图象在第一、第三象限;在第一象限内,y随着x的增大而减小;在第三象限内,y随着x的增大而减小.
∵x1<0<x2<x3,
∴y1<0,y2>y3>0,即y1<y3<y2.
故选:C.
18.解:∵反比例函数y=中的6>0,
∴该双曲线位于第一、三象限,且在每一象限内y随x的增大而减小,
∵点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,
∴点A位于第三象限,点B位于第一象限,
∴y1<y2.
故选:C.
19.解:∵函数y=﹣图象关于原点对称,
∴OA=OB,
连接OC,过A作AE⊥x轴于E,过C作CF⊥x轴于F,
∵△ABC是等边三角形,
∴AO⊥OC,
∴∠AOC=90°,∠AOC=30°,
∴∠AOE+∠COF=90°,
设OA=x,则AC=2x,OC=x,
∵AE⊥x轴,CF⊥x轴,
∴∠AEO=∠OFC=∠AOE+∠OAE=90°,
∴∠COF=∠OAE,
∴△AOE∽△OCF,
∴=()2=,
∵顶点A在函数y=﹣图象的两个分支上,
∴S△AOE=,
∴S△OCF=,
∵顶点C始终在函数y=的图象上,
∴k=9,
故选:B.
20.解:延长AD交x轴于C,如图所示:
则AE⊥OC,
∵D的坐标为(4,3),
∴OC=4,CD=3,
∴OD==5,
∵四边形OBAD是菱形,
∴AD=OB=OD=5,
∴AE=5+3=8,
∴点A的坐标为(4,8),
把A(4,8)代入函数y=(x>0)得:k=4×8=32;
故选:A.
21.解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBE,
∵点A的坐标为(4,0),
∴OA=4,
∵AB=5,
∴OB==3,
在△ABO和△BCE中,
,
∴△ABO≌△BCE(AAS),
∴OA=BE=4,CE=OB=3,
∴OE=BE﹣OB=4﹣3=1,
∴点C的坐标为(﹣3,1),
∵反比例函数y=(k≠0)的图象过点C,
∴k=xy=﹣3×1=﹣3,
故选:C.
22.解:作CE⊥OB于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∴∠OBA+∠CBE=90°,
∵∠OBA+∠OAB=90°,
∴∠OAB=∠CBE,
∵∠AOB=∠CEB,
∴△AOB≌△BEC(AAS),
∴OA=BE,OB=CE,
∵点A的坐标为(2,0),点B的坐标为(0,4).
∴OA=2,OB=4,
∴BE=2,CE=4,
∴C(4,6),
∵反比例函数y=(k≠0)的图象经过点C,
∴k=4×6=24,
故答案为:24.
五.待定系数法求反比例函数解析式
23.解:分别过A、B作AE⊥x轴于E,BD⊥y轴交AE于F.
∵顶点A在反比例函数y=图象上,
∴S△AOE=2.
∵∠OAB=90°,
∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,
∴△OAE∽△ABF,
∴OA:AB=OE:AF=AE:BF,
在Rt△AOB中,∠AOAB=90°,∠OBA=30°,
∴OA:AB=1:,
∴=()2=3,
∵S△AOE=4=2,
∴S△ABF=6,
∴S△BCD=S△ABF=,
∵Rt△AOB的面积恰好被y轴平分,
∴AC=BC,
作AM∥OE交y轴于M,易证得△CDB≌△CMA,
∴S△CAM=
∴S△AOC=2+=,
∴S△BOC=S△AOC=,
∴S△BOD=+=5,
∴k=2S△BOD=10,
∴过点B的反比例函数的解析式为y=
故答案为:y=.
六.反比例函数与一次函数的交点问题
24.解:根据题意设A(t,),
∵正比例函数y=kx与函数y=的图象交于A,B两点,
∴B(﹣t,﹣),
∵BC∥x轴,AC∥y轴,
∴C(t,﹣),
∴S△ABC=BC AC=×[t﹣(﹣t)]×[﹣(﹣)]=12;
故选:C.
25.解:观察函数图象可知,当﹣1<x<0或x>2时,一次函数y1=k1x+b的图象在反比例函数y2=的图象的下方,
∴不等式k1x+b<的解集为:﹣1<x<0或x>2,
故选:A.
26.解:∵正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,
∴B(2,﹣m),
∴不等式ax>的解集为x<﹣2或0<x<2,
故选:D.
27.解:设点B的坐标为(m,),
∵S△BCD=5,且a>1,
∴×m×=5,
解得:a=11,
故选:D.
28.解:∵直线l∥y轴,
∴∠OMP=∠OMQ=90°,
∴S△OMP=×8=4,S△OMQ=﹣k.
又S△POQ=15,
∴4﹣k=15,
即k=11,
∴k=﹣22.
故选:D.
29.解:(1)把A(2,1)代入y=的得:k=2×1=2,
∴反比例函数的解析式是y=,
∵B(﹣1,m)代入反比例函数y=得:m=﹣2,
∴B的坐标是(﹣1,﹣2),
把A、B的坐标代入一次函数y=ax+b得,
解得:a=1,b=﹣1,
∴一次函数的解析式是y=x﹣1;
(2)把y=0代入一次函数的解析式是y=x﹣1得:x﹣1=0,
解得x=1,
∴C(1,0),
∴S△AOB=SAOC+S△BOC=+=.
30.解:(1)把A(2,5)代入中,得到m=10,
∴反比例函数的解析式为y=,
把B(n,2)代入y=中,得到n=5.
(2)∵一次函数y=kx+b的图象过点A(2,5)和点B(5,2).
∴,解得,
∴一次函数为y=﹣x+7,
令y=0,则﹣x+7=0,解得x=7,
∴C(7,0),
∴S△OAB=S△OAC﹣S△BOC=﹣=.
31.解:(1)∵一次函数y1=x+b的图象与反比例函数y2=的图象相交于点A(2,3),
∴3=2+b,3=,
∴b=1,k=6,
∴一次函数和反比例函数的解析式分别是y1=x+1、y2=;
(2)把x=﹣3代入y=x+1得,y=﹣2,
∴B(﹣3,﹣2),
观察图象,y1≤y2时,x的取值范围是x≤﹣3或0<x≤2;
(3)把x=0代入y1=x+1得,y=1,
∴C(0,1),
∴S△AOB=S△AOC+S△BOC=×(2+3)=.
32.解:(1)∵B(n,﹣4)是一次函数y=x+n的图象上的点,
∴﹣4=n+n,
∴n=﹣2,
∴B(﹣2,﹣4),一次函数为:y=x﹣2,
∵反比例函数y=的图象过点B,
∴k=﹣2×(﹣4)=8,
∴反比例函数的解析式为y=,
(2)设C是直线AB与x轴的交点,
∴当y=0时,x=﹣2.
∴点C(﹣2,0),
∴OC=2.
∴S△AOB=S△ACO+S△BCO==6;
(3)∵点A(4,m)在直线y=x﹣2上,
∴m=4﹣2=2,
∴A(4,2),
∴AB==6,
设点O到直线AB的距离为h,
∴AB h=6,
∴h==,
∴点O到直线AB的距离为;
(4)不等式x+n>的解集为:﹣2<x<0或x>4.
故答案为:﹣2<x<0或x>4.
33.解:(1)在Rt△AOB中,OA=8,OE=OB=4.
∴点A,B的坐标分别为(﹣8,0),(0,4),
将点A,B的坐标代入直线的表达式,得,
解得,
∴直线AB的表达式为y1=x+4,
当x=4时,y1=x+4=6,
∴点C的坐标为(4,6),
将点C的坐标代入y2=得:6=,
解得m=24,
∴反比例函数的表达式y2=;
(2)存在,
设点P的坐标为(0,t)
则S△CEO=CE OE=6×4=12,
而S△ABP=BP OA=×|4﹣t|×8=4×|4﹣t|=12,
解得t=1或﹣7,
∴点P的坐标为(0,1)或(0,﹣7).
34.解:(1)∵y2的图象经过点(1,2),
∴把点坐标代入y2解析式得2=,k=2,
∵y1的图象也经过点(1,2),
∴把点坐标和k=2代入y1解析式得2=a+1﹣2,a=3,
①两个函数的解析式分别为:
y1=3x﹣1;y2=;
②y1>y2,
y1=3x﹣1;y2=;联立方程组,
,
解得和,
由此可知函数y1、y2 有两个交点,分别是(1,2)(﹣,﹣3)
两函数图象如下图
由函数图象可知,在第一象限y1>y2 时,x>1;在第三象限y1>y2 时,﹣<x<0;
(2)∵直线x=m分别交函数y1和y2的图象于点A(xA,yA),B(xB,yB),且点B到x轴的距离为2,
∴B(1,2)或(﹣1,﹣2),
∵yA﹣yB=2,
∴yA=4或0,
∴A(1,4)或(﹣1,0),
把(1,4)代入y1=ax+1﹣k得,4=a+1﹣k,解得a=5;
把(﹣1,0)代入y1=ax+1﹣k得,0=﹣a+1﹣k,解得a=﹣1;
故a的值为5或﹣1.
35.解:(1)将代入y=k1x与,得,,
解得,k2=3.
故答案为:,3;
(2)由(1)可得反比例函数的表达式为,
将x=1代入,得y=3,
∴P(1,3),
设直线l的函数表达式为y=mx+n,
将P(1,3),代入得,
解得,
∴直线l的函数表达式为.
(3)在中,令x=0,得,
∴A(0,)
∴直线OC沿射线CP方向平移,平移后的直线过点A时,直线的函数表达式为.
在中,令y=0,得x=﹣42,
∴直线OC在平移过程中与x轴交点的横坐标的取值范围是﹣42≤x≤0.
36.解:(1)将点A(﹣4,﹣1)代入y=(k2≠0)得,k2=4,
∴反比例函数的解析式为y=,
将点B(a,3)代入y=得,a=,
∴B(,4),
将点A、B的坐标代入y=k1x+b得,
解得,
∴一次函数的解析式为y=x+2;
(2)设直线AB交y轴于点C
令x=0,解得y=2,
∴OC=2,
∴△OAB的面积=△OCA的面积+△OCB的面积,
=OC |xA|+OC |yB|
=
=;
(3)由题意,OP∥AB,
∴直线OP的函数关系式为y=x
由题意,列方程组,
解得或,
∴点P的坐标为(,)或(﹣,﹣).
七.反比例函数与一次函数的交点问题
37.解:(1)把A(1,3)代入y=得,3=,
∴k=3,
∴反比例函数为y=,
把B(m,1)代入y=得,1=,
解得m=3,
∴B(3,1),
把A(1,3),B(3,1)代入y=ax+b得,
解得:,
∴一次函数为y=﹣x+4;
(2)∵0<x<1或x>3时,反比例函数为常数)的图象在一次函数y=ax+b的图象的上方,
∴若点P到点M的距离小于线段PN的长度,n的取值范围是0<n<1或n>3.
八.反比例函数综合题
38.解:(1)∵点A在一次函数y1=x+2①的图象上,且点A的横坐标为﹣3,
∴A(﹣3,﹣1),
∵点A在反比例函数y2=的图象上,
∴k=﹣3×(﹣1)=3,
∴反比例函数的表达式为y2=②,
联立①②解得,或,
∴B(1,3);
(2)由(1)知,A(﹣3,﹣1),B(1,3),
由图象知,当y1<y2时,x的取值范围为x<﹣3或0<x<1;
(3)如图,连接OP,交AB于H,
∵四边形PAOB是菱形,
∴OP⊥AB,AH=BH,
由(1)知,A(﹣3,﹣1),B(1,3),
∴AB==4,点H(﹣1,1),
∴OH=,
∴S菱形PAOB=2S△AOB=2×AB OH=AB OH=4×=8.
39.解:(1)将A(a,3)代入y2=﹣x得,
﹣=3,
∴a=﹣2,
∴A(﹣2,3),
将A(﹣2,3)代入y1=得,
∴k=﹣2×3=﹣6,
∵点A与B关于原点对称,
∴B(2,﹣3);
(2)由图象知,当x<﹣2或0<x<2时,x;
(3)作AH⊥BC于H,
∵A(﹣2,3),B(2,﹣3),
∴AH=6,BH=4,
由勾股定理得,AB=2,
∵四边形ABCD是菱形,
∴BC=AB=2,
∴菱形ABCD的面积为2×6=12.
40.解:(1)∵点A(4,n)是反比例函数y=(x>0)图象上的一点,
∴4n=8,
解得n=2,
∴点A(4,2),
设直线OA的解析式:y=kx(k≠0),
将点A(4,2)代入解析式,
得4k=2,
解得k=,
∴直线OA的解析式:y=x;
(2)设反比例函数y=(x>0)的图象上点M′绕原点O逆时针旋转45°后到点M,
过点M′作M′H⊥x轴于点H,如图所示:
则∠M′HO=90°,
∵∠MOM′=45°,
∴∠M′OH=45°,
∴∠OM′H=45°,
∴OH=M′H,
设OH=M′H=t,
∴点M′(t,t),
∵点M′在反比例函数y=(x>0)的图象上,
∴t2=8,
解得t=或﹣(舍),
∴OH=M′H=,
根据勾股定理,得OM′=4,
∴OM=4;
(3)过点A作AC⊥OA,交OB于点C,过点A作AG⊥x轴于点G,过点C作CK⊥AG,交GA的延长线于点K,如图所示:
则∠OGA=90°,∠K=90°,∠OAC=90°,
∴∠OAG+∠AOG=90°,∠CAK+∠OAG=90°,
∴∠AOG=∠CAK,
∵∠AOB=45°,
∴∠OCA=45°,
∴AC=AO,
∴△OGA≌△AKC(AAS),
∴OG=AK,AG=CK,
∵A(4,2),
∴AK=OG=4,CK=AG=2,
∴点C坐标为(2,6),
设直线OB的解析式:y=mx(k≠0),
将点C坐标代入解析式,
得2m=6,
解得m=3,
∴直线OB的解析式:y=3x,
联立,
解得或(舍去),
∴点B坐标为(,).
一.反比例函数的图象
1.已知y=(m+1)xm+2是反比例函数,则函数的图象在( )
A.第一、二象限 B.第二、四象限
C.第一、三象限 D.第三、四象限
2.函数y=﹣的大致图象是( )
A.B.C.D.
3.如果矩形面积为6cm2,那么它的长ycm与宽xcm之间函数关系用图象表示大致是( )
A.B.C.D.
二.反比例函数的性质
4.下列函数y=﹣8x,y=5x﹣1,y=,y=(x>0),y=﹣(x<0)中,y随x的增大而减小的( )
A.4个 B.3个 C.2个 D.1个
5.已知反比例函数y=,下列结论中不正确的是( )
A.其图像经过点(﹣1,﹣3) B.其图像分别位于第一、第三象限
C.当x<0时,y随x的增大而增大 D.当x>1时,0<y<3
6.如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
﹣1 B.﹣2
C.﹣3 D.﹣4
三.反比例函数系数k的几何意义
7.如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图象经过点A,若S△OAB=1,则k的值为 .
8.如图,点A是反比例函数的图象上任意一点,AB∥x轴交反比例函数的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,则S四边形ABCD为( )
A.2﹣a B.﹣a C.﹣2a D.2+a
9.如图,在平面直角坐标系中, ABCD的三个顶点坐标分别为A(1,0),B(4,2),C(2,3),第四个顶点D在反比例函数y=(x<0)的图象上,则k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
10.如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
11.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A.2 B.1 C.﹣1 D.﹣2
12.如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )
A.3 B.﹣3 C. D.
13.如图,点A是反比例函数y=(x>0)图象上的任意一点,过点A作AB垂直x轴交反比例函数y=(x>0)的图象于点B,连接AO、BO,若△ABO的面积为1.5,则k的值为 .
14.如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k= .
15.如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .
16.如图,点A、B在反比例函数的图象上,AC⊥y轴,垂足为D,BC⊥AC.若四边形AOBC的面积为6,,则k的值为 .
四.反比例函数图象上点的坐标特征
17.在反比例函数(k为常数)上有三点A(x1,y1),B(x2,y2),C(x3,y3),若x1<0<x2<x3,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y2<y1
18.已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
19.如图,等边△ABC的顶点A,B分别在函数y=﹣图象的两个分支上,且AB经过原点O.当点A在函数y=﹣的图象上移动时,顶点C始终在函数y=的图象上移动,则k的值为( )
A.6 B.9 C.2 D.3
20.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(k>0,x>0)的图象上,点D的坐标为(4,3)则k的值为( )
A.32 B.24 C.20 D.12
21.如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则k的值为( )
A.4 B.﹣4 C.﹣3 D.3
22.正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
五.待定系数法求反比例函数解析式
23.如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则经过点B的反比例函数的解析式为 .
六.反比例函数与一次函数的交点问题
24.如图,正比例函数y=kx与反比例函数y=的图象交于A,B两点,BC∥x轴,AC∥y轴,则S△ABC=( )
A.10 B.11 C.12 D.13
25.如图,一次函数y1=k1x+b与反比例函数y2=的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式k1x+b<的解集是( )
A.﹣1<x<0或x>2 B.x<﹣1或0<x<2
C.x<﹣1或x>2 D.﹣1<x<2
26.如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A.x<﹣2或x>2 B.﹣2<x<2
C.﹣2<x<0或x>2 D.x<﹣2或0<x<2
27.如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
28.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=和y=的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
29.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1),点B的坐标为(﹣1,m).
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积.
30.如图一次函数y=kx+b的图象与反比例函数的图象交于点A(2,5)和点B(n,2).
(1)求m,n的值;
(2)连接OA,OB,求△OAB的面积.
31.如图,一次函数y1=x+b的图象与反比例函数y2=的图象相交于点A(2,3)和B两点,点B的横坐标是﹣3.
(1)求一次函数和反比例函数的解析式;
(2)直接写出y1≤y2时,x的取值范围;
(3)求△AOB的面积.
32.如图,已知点A(4,m)、B(n,﹣4)是一次函数y=x+n的图象与反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)求点O到直线AB的距离;
(4)请直接写出关于x的不等式x+n>的解集: .
33.如图,平面直角坐标系中,直线y1=kx+b(k、b为常数,k≠0)分别与x,y轴相交于点A,B,与双曲线y2=(m为常数,m≠0)分别交于点C,D(点C在第一象限,点D在第三象限),作CE⊥x轴于点E.已知OA=8,OE=OB=4.
(1)求直线y1和双曲线y2的解析式;
(2)在y轴上是否存在一点P,使S△ABP=S△CEO?若存在,请求出P的坐标:若不存在,请说明理由.
34.已知函数y1=ax+1﹣k,y2=,其中a,k都为常数,且ak≠0.y2的图象经过点(1,2).
(1)若y1的图象也经过点(1,2).
①求这两个函数的解析式.
②当y1>y2时,求x的取值范围.
(2)直线x=m分别交函数y1和y2的图象于点A(xA,yA),B(xB,yB),且点B到x轴的距离为2,若yA﹣yB=2,求a的值.
35.如图,一次函数y=k1x的图象与反比例函数y=(x>0)的图象交于点C(6,),且横坐标为1的点P也在反比例函数y=(x>0)的图象上,另有一直线l经过点P,C.
(1)k1= ,k2= .
(2)求直线l的函数表达式;
(3)设直线l与y轴交于点A,将直线OC沿射线CP方向平移至点A处停止,请求出直线OC在平移过程中与x轴交点的横坐标的取值范围.
36.如图,一次函数y=k1x+b(k1≠0)与反比例函数y=(k2≠0)的图象交于点A(﹣4,﹣1)和点B(a,3).
(1)求反比例函数和一次函数的关系式;
(2)求△OAB的面积;
(3)P是直线AB下方反比例函数图象上一点,且△PAB的面积与△OAB的面积相等,求点P的坐标.
七.反比例函数与一次函数的交点问题
37.如图,已知反比例函数为常数)的图象与一次函数y=ax+b的图象交于A(1,3),B(m,1)两点.
(1)求反比例函数及一次函数的表达式;
(2)已知点P(n,0),过点P作平行于y轴的直线,交一次函数图象于点M,且点M在第一象限内,交反比例函数图象于点N.若点P到点M的距离小于线段PN的长度,结合函数图象直接写出n的取值范围.
八.反比例函数综合题
38.如图1,一次函数y1=x+2与反比例函数交于A,B两点,点A的横坐标为﹣3.
(1)求出反比例函数的表达式及点B的坐标;
(2)当y1<y2时,直接写出x的取值范围;
(3)如图2,在第二象限中存在一点P,使得四边形PAOB是菱形,求菱形PAOB的面积.
39.如图,反比例函数y1=(k≠0)的图象与正比例函数y2=﹣x的图象相交于A(a,3)B两点.
(1)求k的值及B点的坐标;
(2)直接写出不等式x的解集;
(3)已知AD∥x轴,以AB、AD为边作菱形ABCD,求菱形ABCD的面积.
40.已知:如图1,点A(4,n)是反比例函数y=(x>0)图象上的一点.
(1)求n的值和直线OA的解析式;
(2)如图2,将反比例函数y=(x>0)的图象绕原点O逆时针旋转45°后,与y轴交于点M,求线段OM的长度;
(3)如图3,将直线OA绕原点O逆时针旋转45°,与反比例函数y=(x>0)的图象交于点B,求点B的坐标.
参考答案
一.反比例函数的图象
1.解:依题意有m+2=﹣1,
解得m=﹣3,
因而函数是y=,
故函数经过第二、四象限.
故选:B.
2.解:因为k=﹣2,y=﹣<0,所以它的两个分支分别位于第三、四象限.
故选:D.
3.解:由矩形的面积公式可得xy=6,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
二.反比例函数的性质
4.解:∵y=﹣8x中,k=﹣8<0,
∴y随x增大而减小;
∵y=5x﹣1中,k=5>0,
∴y随x增大而增大;
∵y=中,k=6>0,
∴在一、三象限内,y随x增大而减小.
∵y=(x>0),
∴当x>0,y随x增大而减小,
∵y=﹣(x<0)中,k=﹣1<0,
∴当x<0,y随x增大而增大;
故选:C.
5.解:将(﹣1,﹣3)代入解析式,得﹣3=﹣3,故A正确,不符合题意;
由于k=3>0,则函数图象过一、三象限,在每个象限内,y随x的增大而减小,故B正确,不符合题意、C错误,符合题意;
∵x=1时,y=3,且当x>0时y随x的增大而减小
∴当x>1时,0<y<3,故D正确,不符合题意,
故选:C.
6.解:∵点E为OC的中点,
∴△AEO的面积=△AEC的面积=,
∵点A,C为函数y=(x<0)图象上的两点,
∴S△ABO=S△CDO,
∴S四边形CDBE=S△AEO=,
∵EB∥CD,
∴△OEB∽△OCD,
∴=()2,
∴S△OCD=1,
则xy=﹣1,
∴k=xy=﹣2.
故选:B.
三.反比例函数系数k的几何意义
7.解:设A(a,b),如图,作A 过x轴的垂线与x 轴交于C,
则:AC=b,OC=a,AC∥OB,
∴∠ACD=∠BOD=90°,∠ADC=∠BDO,
∵BD=AD,
∴△ADC≌△BDO(AAS),
∴S△ADC=S△BDO,
∴S△OAC=S△AOD+S△ADC=S△AOD+S△BDO=S△AOB=1,
∴×OC×AC=ab=1,
∴ab=2,
∵A(a,b) 在y=上,
∴k=ab=2.
故答案为:2.
8.解:连接OA、OB,AB交y轴于E,如图,
∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA==1,S△OBE=|a|=﹣a,
∴S△OAB=1﹣a,
∵四边形ABCD为平行四边形,
∴S四边形ABCD=2S△OAB=2﹣a.
故选:A.
9.解:过点D作DE⊥x轴于点E,CF⊥x轴于F,作BH∥x轴,交CF于H,
∵A(1,0),B(4,2),C(2,3),
∴BH=4﹣2=2,CH=3﹣2=1,
∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∴∠DAB+∠ABC=180°,
∵BH∥x轴,
∴∠ABH=∠BAF,
∵∠DAE+∠BAF+∠DAB=180°=∠CBH+∠ABH+∠DAB,
∴∠DAE=∠CBH,
在△ADE和△BCH中,
,
∴△ADE≌△BCH(AAS),
∴AE=BH=2,DE=CH=1,
∴OE=1,
∴点D坐标为(﹣1,1),
∵点D在反比例函数y=(x<0)的图象上,
∴k=﹣1×1=﹣1,
故选:A.
10.解:∵点A在函数y=(x>0)的图象上,
∴S△AOC=×2=1,
又∵点B在反比例函数y=﹣(x<0)的图象上,
∴S△BOC=×8=4,
∴S△AOB=S△AOC+S△BOC
=1+4
=5,
故选:B.
11.解:设B(a,),
∵四边形OBAD是平行四边形,
∴AB∥DO,
∴A(,),
∴AB=a﹣,
∵平行四边形OBAD的面积是5,
∴(a﹣)=5,
解得k=﹣2,
故选:D.
12.解:∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,
∴S△OAM=S△OCN=k1,
∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,
∴S矩形OABC=k2,
∴S矩形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,
∴k2﹣k1=3,
∴k1﹣k2=﹣3,
故选:B.
13.解:设AB与x轴交于点C,
点B在反比例函数y=的图象上,
∴S△BOC=|k|=,
又∵S△AOB=1.5,
∴S△AOC=1.5﹣=1=|k|,
又∵k<0,
∴k=﹣2,
故答案为:﹣2.
14.解:如图,过点E作EH⊥BC于H,
设点A(a,),C(c,0),
∵点E是矩形ABCD的对角线的交点,
∴E(,),
∵点E在反比例函数y=的图象上,
∴=k,
∴c=3a,
∵△OCE的面积为6,
∴OC EH=c =×3a =6,
∴k=8,
故答案为:8.
15.解:因为D为AC的中点,△AOD的面积为3,
所以△AOC的面积为6,
所以k=12=2m.
解得:m=6.
故答案为:6.
16.解:设点,
∵AC⊥y轴,
∴AD=a,,
∵,
∴AC=2a,
∴CD=3a,
∵BC⊥AC.AC⊥y轴,
∴BC∥y轴,
∴点B,
∴,
∵S梯形OBCD=S△AOD+S四边形AOBC,
∴,
解得:k=3.
故答案为:3.
四.反比例函数图象上点的坐标特征
17.解:∵k2≥0,
∴k2+3>0.
∴反比例函数(k为常数)的函数图象在第一、第三象限;在第一象限内,y随着x的增大而减小;在第三象限内,y随着x的增大而减小.
∵x1<0<x2<x3,
∴y1<0,y2>y3>0,即y1<y3<y2.
故选:C.
18.解:∵反比例函数y=中的6>0,
∴该双曲线位于第一、三象限,且在每一象限内y随x的增大而减小,
∵点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,
∴点A位于第三象限,点B位于第一象限,
∴y1<y2.
故选:C.
19.解:∵函数y=﹣图象关于原点对称,
∴OA=OB,
连接OC,过A作AE⊥x轴于E,过C作CF⊥x轴于F,
∵△ABC是等边三角形,
∴AO⊥OC,
∴∠AOC=90°,∠AOC=30°,
∴∠AOE+∠COF=90°,
设OA=x,则AC=2x,OC=x,
∵AE⊥x轴,CF⊥x轴,
∴∠AEO=∠OFC=∠AOE+∠OAE=90°,
∴∠COF=∠OAE,
∴△AOE∽△OCF,
∴=()2=,
∵顶点A在函数y=﹣图象的两个分支上,
∴S△AOE=,
∴S△OCF=,
∵顶点C始终在函数y=的图象上,
∴k=9,
故选:B.
20.解:延长AD交x轴于C,如图所示:
则AE⊥OC,
∵D的坐标为(4,3),
∴OC=4,CD=3,
∴OD==5,
∵四边形OBAD是菱形,
∴AD=OB=OD=5,
∴AE=5+3=8,
∴点A的坐标为(4,8),
把A(4,8)代入函数y=(x>0)得:k=4×8=32;
故选:A.
21.解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBE,
∵点A的坐标为(4,0),
∴OA=4,
∵AB=5,
∴OB==3,
在△ABO和△BCE中,
,
∴△ABO≌△BCE(AAS),
∴OA=BE=4,CE=OB=3,
∴OE=BE﹣OB=4﹣3=1,
∴点C的坐标为(﹣3,1),
∵反比例函数y=(k≠0)的图象过点C,
∴k=xy=﹣3×1=﹣3,
故选:C.
22.解:作CE⊥OB于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∴∠OBA+∠CBE=90°,
∵∠OBA+∠OAB=90°,
∴∠OAB=∠CBE,
∵∠AOB=∠CEB,
∴△AOB≌△BEC(AAS),
∴OA=BE,OB=CE,
∵点A的坐标为(2,0),点B的坐标为(0,4).
∴OA=2,OB=4,
∴BE=2,CE=4,
∴C(4,6),
∵反比例函数y=(k≠0)的图象经过点C,
∴k=4×6=24,
故答案为:24.
五.待定系数法求反比例函数解析式
23.解:分别过A、B作AE⊥x轴于E,BD⊥y轴交AE于F.
∵顶点A在反比例函数y=图象上,
∴S△AOE=2.
∵∠OAB=90°,
∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,
∴△OAE∽△ABF,
∴OA:AB=OE:AF=AE:BF,
在Rt△AOB中,∠AOAB=90°,∠OBA=30°,
∴OA:AB=1:,
∴=()2=3,
∵S△AOE=4=2,
∴S△ABF=6,
∴S△BCD=S△ABF=,
∵Rt△AOB的面积恰好被y轴平分,
∴AC=BC,
作AM∥OE交y轴于M,易证得△CDB≌△CMA,
∴S△CAM=
∴S△AOC=2+=,
∴S△BOC=S△AOC=,
∴S△BOD=+=5,
∴k=2S△BOD=10,
∴过点B的反比例函数的解析式为y=
故答案为:y=.
六.反比例函数与一次函数的交点问题
24.解:根据题意设A(t,),
∵正比例函数y=kx与函数y=的图象交于A,B两点,
∴B(﹣t,﹣),
∵BC∥x轴,AC∥y轴,
∴C(t,﹣),
∴S△ABC=BC AC=×[t﹣(﹣t)]×[﹣(﹣)]=12;
故选:C.
25.解:观察函数图象可知,当﹣1<x<0或x>2时,一次函数y1=k1x+b的图象在反比例函数y2=的图象的下方,
∴不等式k1x+b<的解集为:﹣1<x<0或x>2,
故选:A.
26.解:∵正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,
∴B(2,﹣m),
∴不等式ax>的解集为x<﹣2或0<x<2,
故选:D.
27.解:设点B的坐标为(m,),
∵S△BCD=5,且a>1,
∴×m×=5,
解得:a=11,
故选:D.
28.解:∵直线l∥y轴,
∴∠OMP=∠OMQ=90°,
∴S△OMP=×8=4,S△OMQ=﹣k.
又S△POQ=15,
∴4﹣k=15,
即k=11,
∴k=﹣22.
故选:D.
29.解:(1)把A(2,1)代入y=的得:k=2×1=2,
∴反比例函数的解析式是y=,
∵B(﹣1,m)代入反比例函数y=得:m=﹣2,
∴B的坐标是(﹣1,﹣2),
把A、B的坐标代入一次函数y=ax+b得,
解得:a=1,b=﹣1,
∴一次函数的解析式是y=x﹣1;
(2)把y=0代入一次函数的解析式是y=x﹣1得:x﹣1=0,
解得x=1,
∴C(1,0),
∴S△AOB=SAOC+S△BOC=+=.
30.解:(1)把A(2,5)代入中,得到m=10,
∴反比例函数的解析式为y=,
把B(n,2)代入y=中,得到n=5.
(2)∵一次函数y=kx+b的图象过点A(2,5)和点B(5,2).
∴,解得,
∴一次函数为y=﹣x+7,
令y=0,则﹣x+7=0,解得x=7,
∴C(7,0),
∴S△OAB=S△OAC﹣S△BOC=﹣=.
31.解:(1)∵一次函数y1=x+b的图象与反比例函数y2=的图象相交于点A(2,3),
∴3=2+b,3=,
∴b=1,k=6,
∴一次函数和反比例函数的解析式分别是y1=x+1、y2=;
(2)把x=﹣3代入y=x+1得,y=﹣2,
∴B(﹣3,﹣2),
观察图象,y1≤y2时,x的取值范围是x≤﹣3或0<x≤2;
(3)把x=0代入y1=x+1得,y=1,
∴C(0,1),
∴S△AOB=S△AOC+S△BOC=×(2+3)=.
32.解:(1)∵B(n,﹣4)是一次函数y=x+n的图象上的点,
∴﹣4=n+n,
∴n=﹣2,
∴B(﹣2,﹣4),一次函数为:y=x﹣2,
∵反比例函数y=的图象过点B,
∴k=﹣2×(﹣4)=8,
∴反比例函数的解析式为y=,
(2)设C是直线AB与x轴的交点,
∴当y=0时,x=﹣2.
∴点C(﹣2,0),
∴OC=2.
∴S△AOB=S△ACO+S△BCO==6;
(3)∵点A(4,m)在直线y=x﹣2上,
∴m=4﹣2=2,
∴A(4,2),
∴AB==6,
设点O到直线AB的距离为h,
∴AB h=6,
∴h==,
∴点O到直线AB的距离为;
(4)不等式x+n>的解集为:﹣2<x<0或x>4.
故答案为:﹣2<x<0或x>4.
33.解:(1)在Rt△AOB中,OA=8,OE=OB=4.
∴点A,B的坐标分别为(﹣8,0),(0,4),
将点A,B的坐标代入直线的表达式,得,
解得,
∴直线AB的表达式为y1=x+4,
当x=4时,y1=x+4=6,
∴点C的坐标为(4,6),
将点C的坐标代入y2=得:6=,
解得m=24,
∴反比例函数的表达式y2=;
(2)存在,
设点P的坐标为(0,t)
则S△CEO=CE OE=6×4=12,
而S△ABP=BP OA=×|4﹣t|×8=4×|4﹣t|=12,
解得t=1或﹣7,
∴点P的坐标为(0,1)或(0,﹣7).
34.解:(1)∵y2的图象经过点(1,2),
∴把点坐标代入y2解析式得2=,k=2,
∵y1的图象也经过点(1,2),
∴把点坐标和k=2代入y1解析式得2=a+1﹣2,a=3,
①两个函数的解析式分别为:
y1=3x﹣1;y2=;
②y1>y2,
y1=3x﹣1;y2=;联立方程组,
,
解得和,
由此可知函数y1、y2 有两个交点,分别是(1,2)(﹣,﹣3)
两函数图象如下图
由函数图象可知,在第一象限y1>y2 时,x>1;在第三象限y1>y2 时,﹣<x<0;
(2)∵直线x=m分别交函数y1和y2的图象于点A(xA,yA),B(xB,yB),且点B到x轴的距离为2,
∴B(1,2)或(﹣1,﹣2),
∵yA﹣yB=2,
∴yA=4或0,
∴A(1,4)或(﹣1,0),
把(1,4)代入y1=ax+1﹣k得,4=a+1﹣k,解得a=5;
把(﹣1,0)代入y1=ax+1﹣k得,0=﹣a+1﹣k,解得a=﹣1;
故a的值为5或﹣1.
35.解:(1)将代入y=k1x与,得,,
解得,k2=3.
故答案为:,3;
(2)由(1)可得反比例函数的表达式为,
将x=1代入,得y=3,
∴P(1,3),
设直线l的函数表达式为y=mx+n,
将P(1,3),代入得,
解得,
∴直线l的函数表达式为.
(3)在中,令x=0,得,
∴A(0,)
∴直线OC沿射线CP方向平移,平移后的直线过点A时,直线的函数表达式为.
在中,令y=0,得x=﹣42,
∴直线OC在平移过程中与x轴交点的横坐标的取值范围是﹣42≤x≤0.
36.解:(1)将点A(﹣4,﹣1)代入y=(k2≠0)得,k2=4,
∴反比例函数的解析式为y=,
将点B(a,3)代入y=得,a=,
∴B(,4),
将点A、B的坐标代入y=k1x+b得,
解得,
∴一次函数的解析式为y=x+2;
(2)设直线AB交y轴于点C
令x=0,解得y=2,
∴OC=2,
∴△OAB的面积=△OCA的面积+△OCB的面积,
=OC |xA|+OC |yB|
=
=;
(3)由题意,OP∥AB,
∴直线OP的函数关系式为y=x
由题意,列方程组,
解得或,
∴点P的坐标为(,)或(﹣,﹣).
七.反比例函数与一次函数的交点问题
37.解:(1)把A(1,3)代入y=得,3=,
∴k=3,
∴反比例函数为y=,
把B(m,1)代入y=得,1=,
解得m=3,
∴B(3,1),
把A(1,3),B(3,1)代入y=ax+b得,
解得:,
∴一次函数为y=﹣x+4;
(2)∵0<x<1或x>3时,反比例函数为常数)的图象在一次函数y=ax+b的图象的上方,
∴若点P到点M的距离小于线段PN的长度,n的取值范围是0<n<1或n>3.
八.反比例函数综合题
38.解:(1)∵点A在一次函数y1=x+2①的图象上,且点A的横坐标为﹣3,
∴A(﹣3,﹣1),
∵点A在反比例函数y2=的图象上,
∴k=﹣3×(﹣1)=3,
∴反比例函数的表达式为y2=②,
联立①②解得,或,
∴B(1,3);
(2)由(1)知,A(﹣3,﹣1),B(1,3),
由图象知,当y1<y2时,x的取值范围为x<﹣3或0<x<1;
(3)如图,连接OP,交AB于H,
∵四边形PAOB是菱形,
∴OP⊥AB,AH=BH,
由(1)知,A(﹣3,﹣1),B(1,3),
∴AB==4,点H(﹣1,1),
∴OH=,
∴S菱形PAOB=2S△AOB=2×AB OH=AB OH=4×=8.
39.解:(1)将A(a,3)代入y2=﹣x得,
﹣=3,
∴a=﹣2,
∴A(﹣2,3),
将A(﹣2,3)代入y1=得,
∴k=﹣2×3=﹣6,
∵点A与B关于原点对称,
∴B(2,﹣3);
(2)由图象知,当x<﹣2或0<x<2时,x;
(3)作AH⊥BC于H,
∵A(﹣2,3),B(2,﹣3),
∴AH=6,BH=4,
由勾股定理得,AB=2,
∵四边形ABCD是菱形,
∴BC=AB=2,
∴菱形ABCD的面积为2×6=12.
40.解:(1)∵点A(4,n)是反比例函数y=(x>0)图象上的一点,
∴4n=8,
解得n=2,
∴点A(4,2),
设直线OA的解析式:y=kx(k≠0),
将点A(4,2)代入解析式,
得4k=2,
解得k=,
∴直线OA的解析式:y=x;
(2)设反比例函数y=(x>0)的图象上点M′绕原点O逆时针旋转45°后到点M,
过点M′作M′H⊥x轴于点H,如图所示:
则∠M′HO=90°,
∵∠MOM′=45°,
∴∠M′OH=45°,
∴∠OM′H=45°,
∴OH=M′H,
设OH=M′H=t,
∴点M′(t,t),
∵点M′在反比例函数y=(x>0)的图象上,
∴t2=8,
解得t=或﹣(舍),
∴OH=M′H=,
根据勾股定理,得OM′=4,
∴OM=4;
(3)过点A作AC⊥OA,交OB于点C,过点A作AG⊥x轴于点G,过点C作CK⊥AG,交GA的延长线于点K,如图所示:
则∠OGA=90°,∠K=90°,∠OAC=90°,
∴∠OAG+∠AOG=90°,∠CAK+∠OAG=90°,
∴∠AOG=∠CAK,
∵∠AOB=45°,
∴∠OCA=45°,
∴AC=AO,
∴△OGA≌△AKC(AAS),
∴OG=AK,AG=CK,
∵A(4,2),
∴AK=OG=4,CK=AG=2,
∴点C坐标为(2,6),
设直线OB的解析式:y=mx(k≠0),
将点C坐标代入解析式,
得2m=6,
解得m=3,
∴直线OB的解析式:y=3x,
联立,
解得或(舍去),
∴点B坐标为(,).
