2.3.3点到直线的距离公式 课件(共22张PPT)
文档属性
| 名称 | 2.3.3点到直线的距离公式 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 21:07:28 | ||
图片预览








文档简介
(共22张PPT)
2.3.3点到直线的距离公式
直线与圆的方程
课程标准
探索并掌握点到直线的距离公式;
复习回顾
问题1 直线方程的表达式有哪些?
复习回顾
问题2 两点间的距离公式是什么?
新课导入
上节课,我们学习了如何求点到点的距离
直线
这节课,我们一起探究如何求点到直线的距离
一
二
三
教学目标
点到直线的距离公式的推导与证明
掌握点到直线的距离公式
会用距离公式解决实际问题
教学目标
难点
重点
新知探究
探究一:点到直线的距离公式
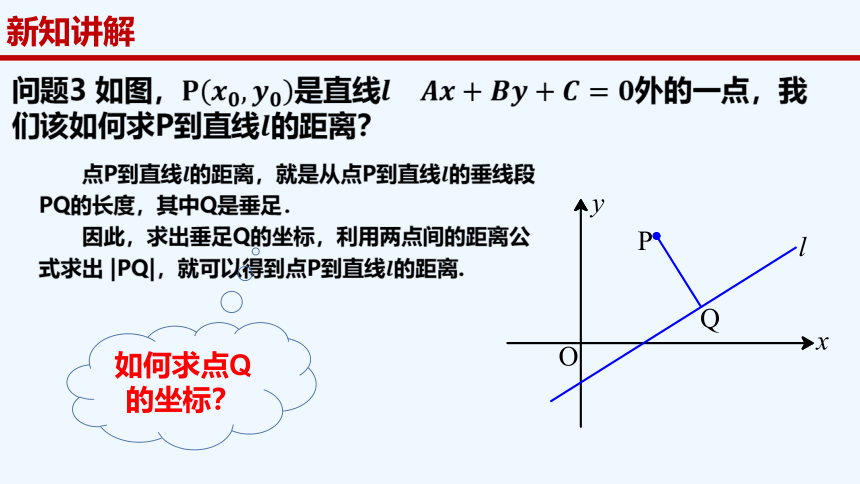
新知讲解
如何求点Q的坐标?
新知讲解
追问1 如何求点Q的坐标?
新知讲解
概念生成
分子的式子是直线方程的一般式形式
分母的式子是直线方程的一般式的系数平方和,开根号
所以,点到直线的距离公式中
直线要化成一般式方程
新知讲解
追问2 上述方法中,我们根据点到直线距离的定义,将点到直线的距离转化为两点之间的距离.思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗?由此能否给出简化运算的方法?
新知讲解
运算的小技巧:整体法(减少未知量)
新知讲解
问题4 向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
新知讲解
新知讲解
利用向量的投影进行运算!
推导(运算)小结
上述两种方法:
第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;
第二种方法利用向量投影,通过向量运算求出结果,简化了运算.
除了上述两种方法,希望大家在课后阅读文献找找其他推导方法!
新知探究
探究二:点到直线距离公式的运用
课堂练习
化成一般式
课堂练习
还有其他方法吗?
利用两点距离公式求三边长度
利用余弦定理求角
利用正弦定理面积公式进行计算
课堂练习
课堂练习
2.3.3点到直线的距离公式
直线与圆的方程
课程标准
探索并掌握点到直线的距离公式;
复习回顾
问题1 直线方程的表达式有哪些?
复习回顾
问题2 两点间的距离公式是什么?
新课导入
上节课,我们学习了如何求点到点的距离
直线
这节课,我们一起探究如何求点到直线的距离
一
二
三
教学目标
点到直线的距离公式的推导与证明
掌握点到直线的距离公式
会用距离公式解决实际问题
教学目标
难点
重点
新知探究
探究一:点到直线的距离公式
新知讲解
如何求点Q的坐标?
新知讲解
追问1 如何求点Q的坐标?
新知讲解
概念生成
分子的式子是直线方程的一般式形式
分母的式子是直线方程的一般式的系数平方和,开根号
所以,点到直线的距离公式中
直线要化成一般式方程
新知讲解
追问2 上述方法中,我们根据点到直线距离的定义,将点到直线的距离转化为两点之间的距离.思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗?由此能否给出简化运算的方法?
新知讲解
运算的小技巧:整体法(减少未知量)
新知讲解
问题4 向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
新知讲解
新知讲解
利用向量的投影进行运算!
推导(运算)小结
上述两种方法:
第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;
第二种方法利用向量投影,通过向量运算求出结果,简化了运算.
除了上述两种方法,希望大家在课后阅读文献找找其他推导方法!
新知探究
探究二:点到直线距离公式的运用
课堂练习
化成一般式
课堂练习
还有其他方法吗?
利用两点距离公式求三边长度
利用余弦定理求角
利用正弦定理面积公式进行计算
课堂练习
课堂练习
