2.3.4两条平行线的距离公式 课件(共11张PPT)
文档属性
| 名称 | 2.3.4两条平行线的距离公式 课件(共11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 853.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 21:08:39 | ||
图片预览



文档简介
(共11张PPT)
直线与圆的方程
2.3.4两条平行直线的距
离公式
一
二
三
教学目标
两条平行直线的距离公式的推导与证明
掌握两条平行直线的距离公式
会用距离公式解决实际问题
教学目标
难点
重点
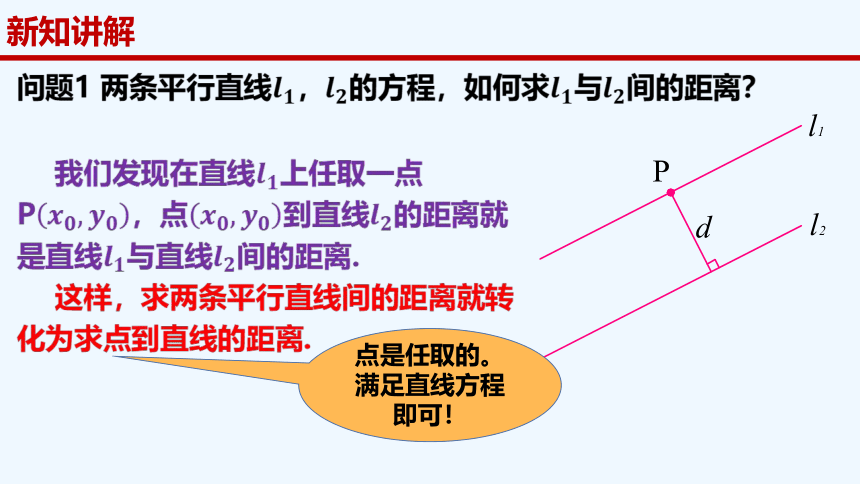
新知讲解
点是任取的。满足直线方程即可!
课堂练习
新知讲解
概念生成
随堂练习
随堂练习
随堂练习
随堂练习
小结
点到直线的距离公式:
我们发现在直线11上任取一点
P(x0,y),点(x0,yo)到直线l2的距离就
是直线1与直线2间的距离
这样,求两条平行直线间的距离就转
化为求点到直线的:更离:
解:先求L与x轴的交点A的坐标。容易知道,点A的坐标为(4,
0).点A到直线2的距离d=
6×4-21×0-1
23
所以L与L2间的距离为
23
证明在直线Ax+By+C1=0上任取一点P(x,yO),点P(x,yO)到直线
Ax+By+C2=0的距离就是这两条平行直线间的距离
即d=
Axo +Byo +C2
VA2+B2
因为点P(xo,yo)在直线Ax十By+C1=0上,所以AxD+ByO
即Ax0+By0=-C1,因此d=
Axo +Byo +C2
+C2
+B2
2
A2+B2
两条平行直线
L:Ax+By+C1=0
L2:Ax+By+C2=0
间的距离为d=
IC1-C21
vA2 B2
解析
(1)在2x+3y-8=0上取一点
(4,0),
12×4+3×0+181
则d=
=2/13.
/22+32
(2)在3x+4y=0上取一点(0,0),将3x
+4y=10化为3x+4y-10=0,则d=
13×0+4×0-101
/32+42
A(1,1),在直线12:x-2y+4=0上取点
B(0,2),设C(x,y),
因为C是AB上靠近A的三等分点,所
以3AC=AB,所以3(x-1,y-1)=(-1,
1),
2
所以
(-1)=-1解得
3
3(y-1)=1,
4
即((号.专)设4:-2+m=0.
则2-2×+m=0,解得m=2,所以1
的方程为x-2y+2=0.
所以点A(1,1)到直线1,的距离
11-2×1+21W5
d=
,即与13间的距
√/12+(-2)2
5
离为
5
直线与圆的方程
2.3.4两条平行直线的距
离公式
一
二
三
教学目标
两条平行直线的距离公式的推导与证明
掌握两条平行直线的距离公式
会用距离公式解决实际问题
教学目标
难点
重点
新知讲解
点是任取的。满足直线方程即可!
课堂练习
新知讲解
概念生成
随堂练习
随堂练习
随堂练习
随堂练习
小结
点到直线的距离公式:
我们发现在直线11上任取一点
P(x0,y),点(x0,yo)到直线l2的距离就
是直线1与直线2间的距离
这样,求两条平行直线间的距离就转
化为求点到直线的:更离:
解:先求L与x轴的交点A的坐标。容易知道,点A的坐标为(4,
0).点A到直线2的距离d=
6×4-21×0-1
23
所以L与L2间的距离为
23
证明在直线Ax+By+C1=0上任取一点P(x,yO),点P(x,yO)到直线
Ax+By+C2=0的距离就是这两条平行直线间的距离
即d=
Axo +Byo +C2
VA2+B2
因为点P(xo,yo)在直线Ax十By+C1=0上,所以AxD+ByO
即Ax0+By0=-C1,因此d=
Axo +Byo +C2
+C2
+B2
2
A2+B2
两条平行直线
L:Ax+By+C1=0
L2:Ax+By+C2=0
间的距离为d=
IC1-C21
vA2 B2
解析
(1)在2x+3y-8=0上取一点
(4,0),
12×4+3×0+181
则d=
=2/13.
/22+32
(2)在3x+4y=0上取一点(0,0),将3x
+4y=10化为3x+4y-10=0,则d=
13×0+4×0-101
/32+42
A(1,1),在直线12:x-2y+4=0上取点
B(0,2),设C(x,y),
因为C是AB上靠近A的三等分点,所
以3AC=AB,所以3(x-1,y-1)=(-1,
1),
2
所以
(-1)=-1解得
3
3(y-1)=1,
4
即((号.专)设4:-2+m=0.
则2-2×+m=0,解得m=2,所以1
的方程为x-2y+2=0.
所以点A(1,1)到直线1,的距离
11-2×1+21W5
d=
,即与13间的距
√/12+(-2)2
5
离为
5
