3.1.1椭圆及其标准方程 课件(共35张PPT)
文档属性
| 名称 | 3.1.1椭圆及其标准方程 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 21:13:05 | ||
图片预览








文档简介
(共35张PPT)
圆锥曲线的方程
第三章
新课导入
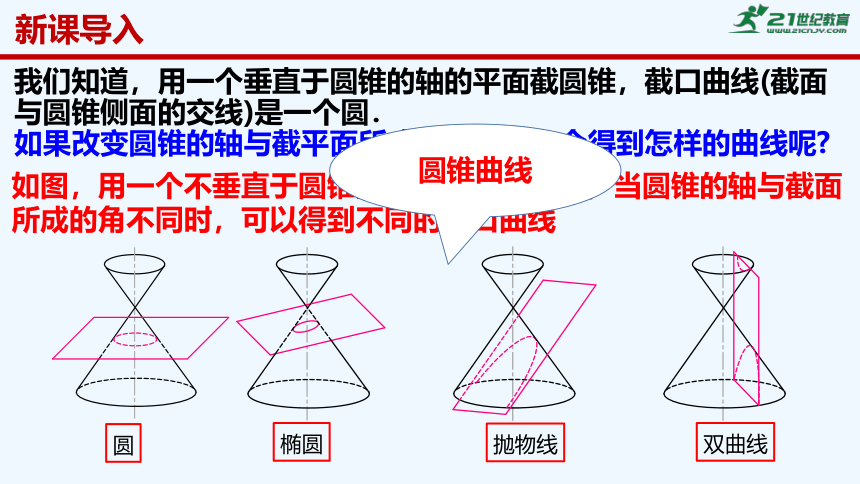
我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.
如果改变圆锥的轴与截平面所成的角,那么会得到怎样的曲线呢
椭圆
抛物线
双曲线
圆
如图,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥的轴与截面所成的角不同时,可以得到不同的截口曲线
圆锥曲线
新课导入
圆锥曲线与科技、生产以及人类生活有着紧密的关系。以上的图片以及生活中很多例子都能说明圆锥曲线在生活中有着广泛的运用!
为什么会有这样广泛的运用?我们将可以从他们的几何性质及其性质中得到答案!
新课导入
圆锥曲线的发现与研究始于古希腊。当时人们用纯几何的方法研究这些与圆密切相关的曲线,它们的几何性质是圆的几何性质的自然推广。17世纪,笛卡尔发明了坐标系,人们开始借助坐标系,运用代数的方法研究圆锥曲线。
本章我们继续采用坐标法,在研究圆锥曲线几何特征的基础上,建立它们的方程,通过方程研究它们的性质,并解决与圆锥曲线有关的几何问题与实际问题。进一步感受数形结合的思想方法,体会坐标法的魅力与威力。
3.1.1椭圆及其标准方程
圆锥曲线的方程
课程标准
了解圆锥曲线的是实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用。
经历从实际情境中抽象出椭圆的过程,掌握椭圆的定义、标准方程及其几何性质。
新课导入
椭圆
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类的生活中具有广泛的运用。那么,椭圆到底有怎样的几何特征?
我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础?
一
二
三
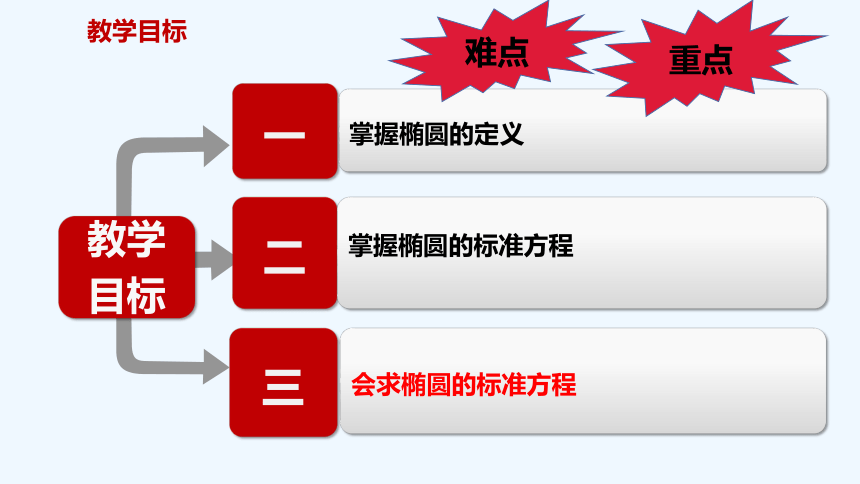
教学目标
掌握椭圆的定义
掌握椭圆的标准方程
会求椭圆的标准方程
教学目标
难点
重点
新知探究
探究一:椭圆的定义
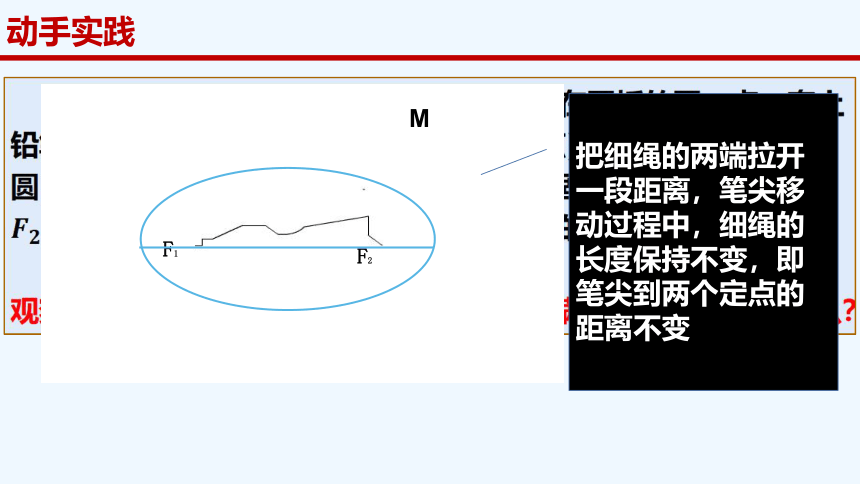
动手实践
F1
F2
M
把细绳的两端拉开一段距离,笔尖移动过程中,细绳的长度保持不变,即笔尖到两个定点的距离不变
概念生成
C
F1
F2
M
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距(一般用2c表示),焦距的一半称为半焦距(用c表示).
新知讲解
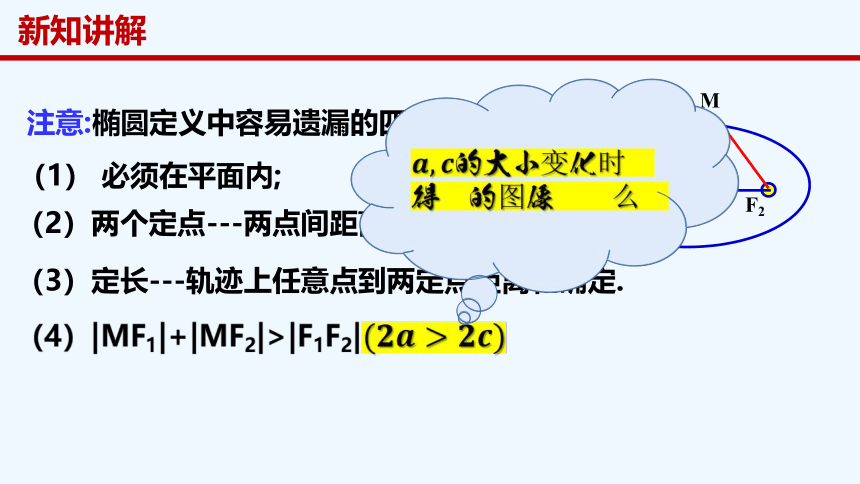
注意:椭圆定义中容易遗漏的四处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)定长---轨迹上任意点到两定点距离和确定.
C
F1
F2
M
合作探究
椭圆
线段AB
不存在
新知讲解
小结:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.
(3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.
(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.
新知探究
探究二:求椭圆的标准方程
新知讲解
问题一:回忆下圆的方程:我们是如何求圆轨迹方程的?
(1)建系
(2)设点
(3)限制条件
(4)代换
(5)化简
求轨迹方程的流程---------建设现代化
类比这个方法,我们开始求取椭圆的标准方程
新知讲解
追问1:我们该如何建系?
C
F1
F2
M
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
O
x
y
O
x
y
F1
F2
M
“对称”、“简洁”
新知讲解
设
限
代
下面怎样化简?
新知讲解
设
限
代
下面怎样化简?
新知讲解
新知讲解
椭圆的标准方程
概念生成
F1
F2
M
0
x
y
追问:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?
概念生成
F1
F2
M
0
x
y
追问:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?
思
新知讲解
追问3:以上的两种标准方程有怎样的特征?
F1
F2
x
y
P
F1
F2
0
x
y
1.方程特征:焦点在坐标轴上,中心在坐标原点的椭圆;
方程的左边是平方和,右边是1.
新知探究
探究三:求椭圆的标准方程
课堂练习
随堂检测
随堂练习
建设限代化
建设限代化
练习解析
随堂练习
由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉伸”得到椭圆吗?如何“拉伸”?由此你能发现椭圆与圆之间的关系吗?
随堂练习
建设限代化
练习解析
随堂检测
定义法
随堂检测
定义
小结
1、椭圆定义:平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
2、椭圆的标准方程:
圆锥曲线的方程
第三章
新课导入
我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.
如果改变圆锥的轴与截平面所成的角,那么会得到怎样的曲线呢
椭圆
抛物线
双曲线
圆
如图,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥的轴与截面所成的角不同时,可以得到不同的截口曲线
圆锥曲线
新课导入
圆锥曲线与科技、生产以及人类生活有着紧密的关系。以上的图片以及生活中很多例子都能说明圆锥曲线在生活中有着广泛的运用!
为什么会有这样广泛的运用?我们将可以从他们的几何性质及其性质中得到答案!
新课导入
圆锥曲线的发现与研究始于古希腊。当时人们用纯几何的方法研究这些与圆密切相关的曲线,它们的几何性质是圆的几何性质的自然推广。17世纪,笛卡尔发明了坐标系,人们开始借助坐标系,运用代数的方法研究圆锥曲线。
本章我们继续采用坐标法,在研究圆锥曲线几何特征的基础上,建立它们的方程,通过方程研究它们的性质,并解决与圆锥曲线有关的几何问题与实际问题。进一步感受数形结合的思想方法,体会坐标法的魅力与威力。
3.1.1椭圆及其标准方程
圆锥曲线的方程
课程标准
了解圆锥曲线的是实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用。
经历从实际情境中抽象出椭圆的过程,掌握椭圆的定义、标准方程及其几何性质。
新课导入
椭圆
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类的生活中具有广泛的运用。那么,椭圆到底有怎样的几何特征?
我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础?
一
二
三
教学目标
掌握椭圆的定义
掌握椭圆的标准方程
会求椭圆的标准方程
教学目标
难点
重点
新知探究
探究一:椭圆的定义
动手实践
F1
F2
M
把细绳的两端拉开一段距离,笔尖移动过程中,细绳的长度保持不变,即笔尖到两个定点的距离不变
概念生成
C
F1
F2
M
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距(一般用2c表示),焦距的一半称为半焦距(用c表示).
新知讲解
注意:椭圆定义中容易遗漏的四处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;
(3)定长---轨迹上任意点到两定点距离和确定.
C
F1
F2
M
合作探究
椭圆
线段AB
不存在
新知讲解
小结:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.
(3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.
(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.
新知探究
探究二:求椭圆的标准方程
新知讲解
问题一:回忆下圆的方程:我们是如何求圆轨迹方程的?
(1)建系
(2)设点
(3)限制条件
(4)代换
(5)化简
求轨迹方程的流程---------建设现代化
类比这个方法,我们开始求取椭圆的标准方程
新知讲解
追问1:我们该如何建系?
C
F1
F2
M
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
O
x
y
O
x
y
F1
F2
M
“对称”、“简洁”
新知讲解
设
限
代
下面怎样化简?
新知讲解
设
限
代
下面怎样化简?
新知讲解
新知讲解
椭圆的标准方程
概念生成
F1
F2
M
0
x
y
追问:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?
概念生成
F1
F2
M
0
x
y
追问:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?
思
新知讲解
追问3:以上的两种标准方程有怎样的特征?
F1
F2
x
y
P
F1
F2
0
x
y
1.方程特征:焦点在坐标轴上,中心在坐标原点的椭圆;
方程的左边是平方和,右边是1.
新知探究
探究三:求椭圆的标准方程
课堂练习
随堂检测
随堂练习
建设限代化
建设限代化
练习解析
随堂练习
由例2我们发现,可以由圆通过“压缩”得到椭圆.你能由圆通过“拉伸”得到椭圆吗?如何“拉伸”?由此你能发现椭圆与圆之间的关系吗?
随堂练习
建设限代化
练习解析
随堂检测
定义法
随堂检测
定义
小结
1、椭圆定义:平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
2、椭圆的标准方程:
