3.2.1双曲线及其标准方程 课件(共26张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 21:15:56 | ||
图片预览






文档简介
(共26张PPT)
3.2.1双曲线及其标准方程
圆锥曲线的方程
课程标准
了解双曲线的定义、几何图形和掌握标准方程
复习回顾
问题1 椭圆的定义和标准方程分别是什么?
1、椭圆定义:平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
2、椭圆的标准方程:
新课导入
双曲线也是具有广泛应用的一种圆锥曲线
本节,我们将类比椭圆的研究方法研究双曲线的有关内容
一
二
三
教学目标
掌握双曲线的几何图形并理解其定义
了解双曲线的标准方程及其推导过程
能根据条件求简单的双曲线的标准方程
教学目标
难点
重点
易错点
新知探究
探究一:掌握双曲线的几何图形并理解其定义
新知讲解
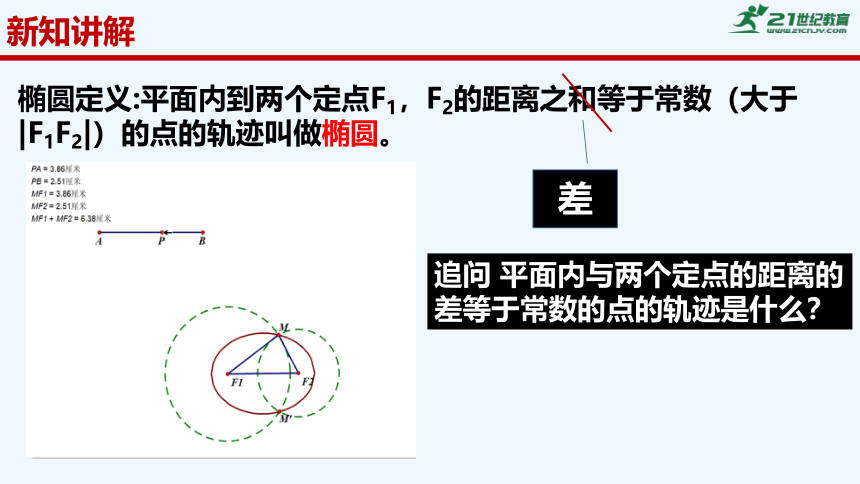
椭圆定义:平面内到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
追问 平面内与两个定点的距离的差等于常数的点的轨迹是什么?
差
新知讲解
椭圆
新知讲解
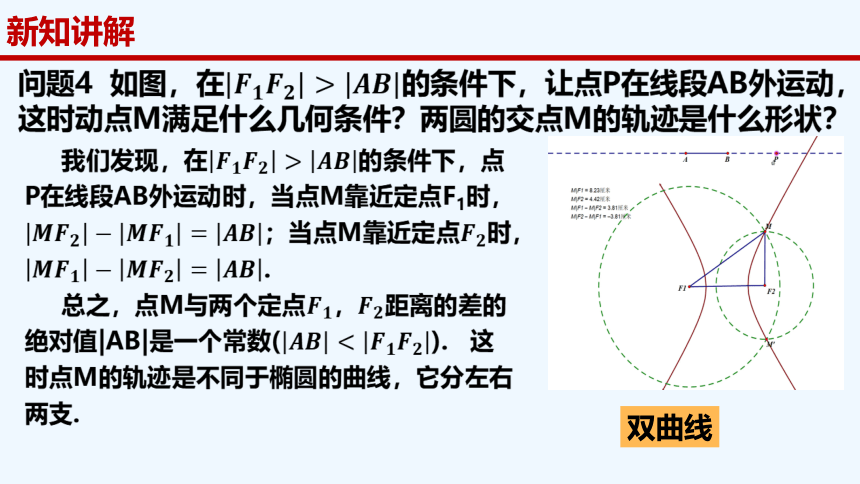
双曲线
概念生成
双曲线定义:一般地,我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
1.必须在平面内
2.两个定点——两点间的距离确定
3.定长——轨迹上任意的点到两个定点的距离之差的绝对值确定
合作探究
双曲线
两条射线
不存在
AB的中垂线
新知讲解
(1)若||MF1|-|MF2||<|F1F2|,M点轨迹为双曲线.
(3)若||MF1|-|MF2||>|F1F2|,M点轨迹不存在.
(2)若||MF1|-|MF2||=|F1F2|,M点轨迹为两条射线.
(4)若||MF1|-|MF2||=0,M点轨迹为AB中垂线.
新知探究
探究二:双曲线的标准方程
新知讲解
问题5 我们是如何求轨迹方程的?
求轨迹方程的流程---------建设限代化
问题6 类比求椭圆标准方程的过程,如何建立适当的坐标系,得出双曲线的方程?
新知讲解
概念生成
新知探究
探究三:根据已知条件求双曲线的标准方程
课堂例题
课堂例题
例2 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程。
合作探究
建设限代化
随堂检测
随堂检测
随堂检测
随堂检测
小结
双曲线的定义、图形及标准方程
双曲线定义:一般地,我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
小结
双曲线与椭圆之间的区别与联系
定 义
方 程
焦 点
a.b.c的关系 椭 圆
双曲线
|MF1|+|MF2|=2a
||MF1|-|MF2||=2a
F(±c,0)
F(0,±c)
F(±c,0)
F(0,±c)
a>b>0,a2=b2+c2
a>0,b>0,但a不一定大于b,c2=a2+b2
3.2.1双曲线及其标准方程
圆锥曲线的方程
课程标准
了解双曲线的定义、几何图形和掌握标准方程
复习回顾
问题1 椭圆的定义和标准方程分别是什么?
1、椭圆定义:平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
2、椭圆的标准方程:
新课导入
双曲线也是具有广泛应用的一种圆锥曲线
本节,我们将类比椭圆的研究方法研究双曲线的有关内容
一
二
三
教学目标
掌握双曲线的几何图形并理解其定义
了解双曲线的标准方程及其推导过程
能根据条件求简单的双曲线的标准方程
教学目标
难点
重点
易错点
新知探究
探究一:掌握双曲线的几何图形并理解其定义
新知讲解
椭圆定义:平面内到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
追问 平面内与两个定点的距离的差等于常数的点的轨迹是什么?
差
新知讲解
椭圆
新知讲解
双曲线
概念生成
双曲线定义:一般地,我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
1.必须在平面内
2.两个定点——两点间的距离确定
3.定长——轨迹上任意的点到两个定点的距离之差的绝对值确定
合作探究
双曲线
两条射线
不存在
AB的中垂线
新知讲解
(1)若||MF1|-|MF2||<|F1F2|,M点轨迹为双曲线.
(3)若||MF1|-|MF2||>|F1F2|,M点轨迹不存在.
(2)若||MF1|-|MF2||=|F1F2|,M点轨迹为两条射线.
(4)若||MF1|-|MF2||=0,M点轨迹为AB中垂线.
新知探究
探究二:双曲线的标准方程
新知讲解
问题5 我们是如何求轨迹方程的?
求轨迹方程的流程---------建设限代化
问题6 类比求椭圆标准方程的过程,如何建立适当的坐标系,得出双曲线的方程?
新知讲解
概念生成
新知探究
探究三:根据已知条件求双曲线的标准方程
课堂例题
课堂例题
例2 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程。
合作探究
建设限代化
随堂检测
随堂检测
随堂检测
随堂检测
小结
双曲线的定义、图形及标准方程
双曲线定义:一般地,我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
小结
双曲线与椭圆之间的区别与联系
定 义
方 程
焦 点
a.b.c的关系 椭 圆
双曲线
|MF1|+|MF2|=2a
||MF1|-|MF2||=2a
F(±c,0)
F(0,±c)
F(±c,0)
F(0,±c)
a>b>0,a2=b2+c2
a>0,b>0,但a不一定大于b,c2=a2+b2
