2022-2023学年湘教版数学七年级上册 2.4 多项式 (第2课时) 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年湘教版数学七年级上册 2.4 多项式 (第2课时) 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 596.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 06:56:51 | ||
图片预览








文档简介
(共24张PPT)
第二章 代数式
2.4 整式
第2课时 多项式
1.理解多项式的概念,会正确识别一个代数式是常项式还是多项式.
2.能说出多项式的项、常数项和次数.
3.能判断一个代数式是不是整式.
◎重点:多项式的有关概念.
◎难点:多项式的次数的确定.
今天是代数式家族的集体活动时间,单项式带着他新结交的朋友来到“单项式俱乐部”门口,可是检察官说什么也不让进门.赶紧解释道:“你看,我可以变成x,也就是数和字母x的积,不也一样可以变身吗? ”
“那你来给它变一变吧!” “好!变成(x+y)……”说到这儿,犹豫了,他挠了挠头.检察官和蔼地对他说:“如果再用乘法分配律继续变形呢?”“那他就变成x+y了!原来他不是单项式啊!”不好意思地连连向检察官道歉,并且把送回了自己的俱乐部.你知道属于哪个俱乐部吗?
答:多项式俱乐部.
多项式与整式
阅读课本本课时 “说一说”与“练习”之间的内容,解决下列问题.
1.填空:(1)2a+3b+5c= 2a + 3b + 5c ;
(2)450-mn= 450 + (-mn) ;
(3)a2-4b2= a2 + (-4b2) .
2a
3b
5c
450
(-mn)
a2
(-4b2)
2.说一说上面三个式子有什么共同特点?
答:都可以看作几个单项式的和.
归纳总结 (1)由几个单项式的 和 组成的代数式叫做多项式,组成多项式的每个 单项式 叫做多项式的项,其中不含 字母 的项叫常数项.
(2)多项式中 次数最高 的项的次数,叫做这个多项式的次数.
(3)单项式和多项式统称为 整式 .
和
单项式
字母
次数最高
整式
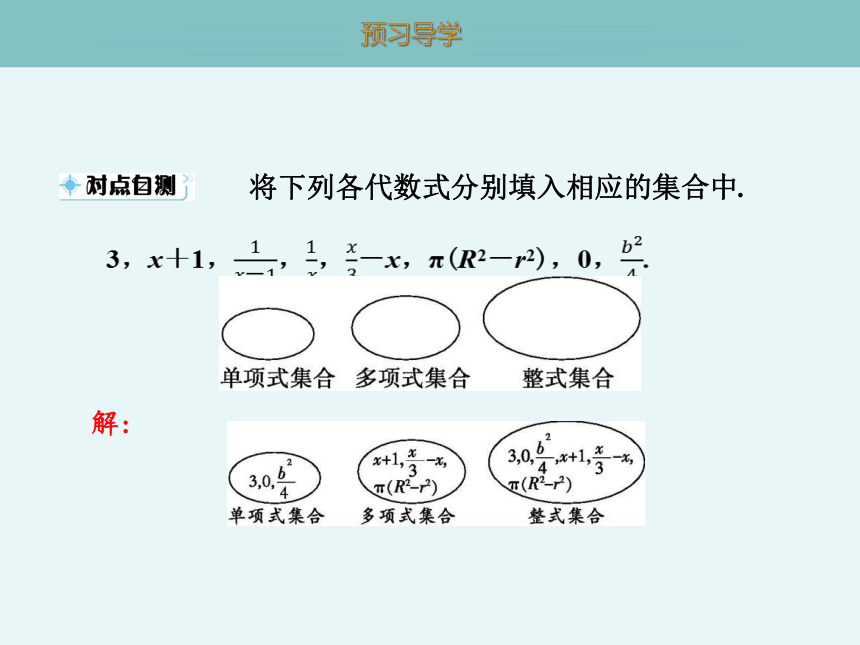
将下列各代数式分别填入相应的集合中.
3,x+1,,,-x,π(R2-r2),0,.
解:
解:
辨别单项式和多项式
1.整式家族的一群孩子迷了路,请你送他们回到各自的“村子”.
-8,2x+y,,ab2,,.
单项式“村子”{ };
多项式“村子”{ }.
解:单项式村子{-8,,ab2 };
多项式村子{2x+y,,}.
方法归纳交流 确定一个代数式是否为多项式,可根据以下三个条件:(1)代数式;(2)含 加减 号;(3)若有分母,分母中不能含有 字母 .
加减
字母
多项式的项、次数的确定
2.写出下列各多项的次数和常数项.
(1)2x2-3x+5;(2)a+b+c-1;
(3)-a2+a2b+2a2b2.
解:(1)2x2-3x+5的次数为2,常数项为5;
(2)a+b+c-1的次数为1,常数项为-1;
(3)-a2+a2b+2a2b2的次数为4,常数项为0.
方法归纳交流 (1)多项式的每一项都包括它前面的符号.(2)多项式的次数是 次数最高项 的次数,不是所有项次数的和.(3)多项式中如果没有常数项,则常数项为 0 .
次数最高项
0
多项式按字母的降幂排列
3.阅读课本习题2.4B组第7题,解决下列问题:已知多项式3x2y2-xy3+5x4y-7y5+y4x6.
(1)它是几次几项式?
(2)把它按y的降幂重新排列;
(3)把它按x的降幂重新排列.
解:(1)3x2y2-xy3+5x4y-7y5+y4x6是十次五项式;
(2)按y的降幂排列为-7y5+y4x6-xy3+3x2y2+5x4y;
(3)按x的降幂排列为y4x6+5x4y+3x2y2-xy3-7y5.
根据条件编写多项式
4.试写出至少两个只含有字母x、y的多项式,且满足下列条件:
(1)六次三项式;
(2)每一项的系数均为1或-1;
(3)不含常数项;
(4)每一项必须同时含字母x、y,但不能含有其他字母.
解:此题答案不唯一,如:x3y3-x2y4+xy5;-x2y4-xy-xy2.
已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3和x2,则( C )
A.m=-5,n=-1 B.m=5,n=1
C.m=-5,n=1 D.m=5,n=-1
C
1在多项式2x2-xy3+18中,次数最高的项是 ( D )
A.2 B.18
C.2x2 D.-xy3
2关于多项式x2-x-2的说法正确的是 ( C )
A.二次项系数是0 B.一次项系数是1
C.常数项是-2 D.它是3次多项式
D
C
33x-2是由 3x 和 -2 两项组成的.
4下列各式-,3xy,a2-b2,,2x>1,-x,0.5+x中,是整式的有 6 个,是单项式的有 3 个,是多项式的有 3 个.
5写出下列多项式的次数和常数项:
(1)3xy+3;
(2)x4-2x3+x-5;
3x
-2
6
3
3
(3)a3-ab2+3a2b2-b3-1.
解:(1)3xy+3的次数是2,常数项是3;
(2)x4-2x3+x-5的次数是4,常数项是-5;
(3)a3-ab2+3a2b2-b3-1的次数是4,常数项是-1.
6多项式x|m|+(m-4)x+7是关于x的四次三项式,则m的值是( C )
A.4 B.-2 C.-4 D.4或-4
C
7把多项式2x2-3x3-x+1按字母x降幂排列,可写成 -3x3+2x2-x+1 .
8已知多项式(m+4)x|m|y2+xy-4x+1是六次四项式,单项式5x2ny6-m与多项式的次数相同,m,n是常数,则mn= 16 .
9已知(3m-4)x3-(2n-3)x2+(2m+5n)x-6是关于x的多项式.
(1)当m,n满足什么条件时,该多项式是关于x的二次多项式;
-3x3+
2x2-x+1
16
(2)当m,n满足什么条件时,该多项式是关于x的三次二项式.
解:(1)由题意得3m-4=0,且2n-3≠0,解得m=,n≠,
所以当m=,n≠时,该多项式是关于x的二次多项式.
(2)由题意得2n-3=0,2m+5n=0,且3m-4≠0,解得n=,m=-,
所以当n=,m=-时,该多项式是关于x的三次二项式.
10已知多项式:x10-x9y+x8y2-…-xy9+y10.
(1)该多项式有什么特点(规律);
(2)按规律写出多项式的第六项,并指出它的次数和系数;
(3)这个多项式是几次几项式?
解:(1)该多项式的特点是每一项的次数都为10次,每项x的次数在减小,y的次数在增加,且x的次数减小量等于y的次数增加量;当x的次数为偶数时,该项的系数为1,当x的次数为奇数时,该项的系数为-1.
(2)根据规律可得第六项为-x5y5,它的系数是-1,次数是10.
(3)这个多项式是十次十一项式.
第二章 代数式
2.4 整式
第2课时 多项式
1.理解多项式的概念,会正确识别一个代数式是常项式还是多项式.
2.能说出多项式的项、常数项和次数.
3.能判断一个代数式是不是整式.
◎重点:多项式的有关概念.
◎难点:多项式的次数的确定.
今天是代数式家族的集体活动时间,单项式带着他新结交的朋友来到“单项式俱乐部”门口,可是检察官说什么也不让进门.赶紧解释道:“你看,我可以变成x,也就是数和字母x的积,不也一样可以变身吗? ”
“那你来给它变一变吧!” “好!变成(x+y)……”说到这儿,犹豫了,他挠了挠头.检察官和蔼地对他说:“如果再用乘法分配律继续变形呢?”“那他就变成x+y了!原来他不是单项式啊!”不好意思地连连向检察官道歉,并且把送回了自己的俱乐部.你知道属于哪个俱乐部吗?
答:多项式俱乐部.
多项式与整式
阅读课本本课时 “说一说”与“练习”之间的内容,解决下列问题.
1.填空:(1)2a+3b+5c= 2a + 3b + 5c ;
(2)450-mn= 450 + (-mn) ;
(3)a2-4b2= a2 + (-4b2) .
2a
3b
5c
450
(-mn)
a2
(-4b2)
2.说一说上面三个式子有什么共同特点?
答:都可以看作几个单项式的和.
归纳总结 (1)由几个单项式的 和 组成的代数式叫做多项式,组成多项式的每个 单项式 叫做多项式的项,其中不含 字母 的项叫常数项.
(2)多项式中 次数最高 的项的次数,叫做这个多项式的次数.
(3)单项式和多项式统称为 整式 .
和
单项式
字母
次数最高
整式
将下列各代数式分别填入相应的集合中.
3,x+1,,,-x,π(R2-r2),0,.
解:
解:
辨别单项式和多项式
1.整式家族的一群孩子迷了路,请你送他们回到各自的“村子”.
-8,2x+y,,ab2,,.
单项式“村子”{ };
多项式“村子”{ }.
解:单项式村子{-8,,ab2 };
多项式村子{2x+y,,}.
方法归纳交流 确定一个代数式是否为多项式,可根据以下三个条件:(1)代数式;(2)含 加减 号;(3)若有分母,分母中不能含有 字母 .
加减
字母
多项式的项、次数的确定
2.写出下列各多项的次数和常数项.
(1)2x2-3x+5;(2)a+b+c-1;
(3)-a2+a2b+2a2b2.
解:(1)2x2-3x+5的次数为2,常数项为5;
(2)a+b+c-1的次数为1,常数项为-1;
(3)-a2+a2b+2a2b2的次数为4,常数项为0.
方法归纳交流 (1)多项式的每一项都包括它前面的符号.(2)多项式的次数是 次数最高项 的次数,不是所有项次数的和.(3)多项式中如果没有常数项,则常数项为 0 .
次数最高项
0
多项式按字母的降幂排列
3.阅读课本习题2.4B组第7题,解决下列问题:已知多项式3x2y2-xy3+5x4y-7y5+y4x6.
(1)它是几次几项式?
(2)把它按y的降幂重新排列;
(3)把它按x的降幂重新排列.
解:(1)3x2y2-xy3+5x4y-7y5+y4x6是十次五项式;
(2)按y的降幂排列为-7y5+y4x6-xy3+3x2y2+5x4y;
(3)按x的降幂排列为y4x6+5x4y+3x2y2-xy3-7y5.
根据条件编写多项式
4.试写出至少两个只含有字母x、y的多项式,且满足下列条件:
(1)六次三项式;
(2)每一项的系数均为1或-1;
(3)不含常数项;
(4)每一项必须同时含字母x、y,但不能含有其他字母.
解:此题答案不唯一,如:x3y3-x2y4+xy5;-x2y4-xy-xy2.
已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3和x2,则( C )
A.m=-5,n=-1 B.m=5,n=1
C.m=-5,n=1 D.m=5,n=-1
C
1在多项式2x2-xy3+18中,次数最高的项是 ( D )
A.2 B.18
C.2x2 D.-xy3
2关于多项式x2-x-2的说法正确的是 ( C )
A.二次项系数是0 B.一次项系数是1
C.常数项是-2 D.它是3次多项式
D
C
33x-2是由 3x 和 -2 两项组成的.
4下列各式-,3xy,a2-b2,,2x>1,-x,0.5+x中,是整式的有 6 个,是单项式的有 3 个,是多项式的有 3 个.
5写出下列多项式的次数和常数项:
(1)3xy+3;
(2)x4-2x3+x-5;
3x
-2
6
3
3
(3)a3-ab2+3a2b2-b3-1.
解:(1)3xy+3的次数是2,常数项是3;
(2)x4-2x3+x-5的次数是4,常数项是-5;
(3)a3-ab2+3a2b2-b3-1的次数是4,常数项是-1.
6多项式x|m|+(m-4)x+7是关于x的四次三项式,则m的值是( C )
A.4 B.-2 C.-4 D.4或-4
C
7把多项式2x2-3x3-x+1按字母x降幂排列,可写成 -3x3+2x2-x+1 .
8已知多项式(m+4)x|m|y2+xy-4x+1是六次四项式,单项式5x2ny6-m与多项式的次数相同,m,n是常数,则mn= 16 .
9已知(3m-4)x3-(2n-3)x2+(2m+5n)x-6是关于x的多项式.
(1)当m,n满足什么条件时,该多项式是关于x的二次多项式;
-3x3+
2x2-x+1
16
(2)当m,n满足什么条件时,该多项式是关于x的三次二项式.
解:(1)由题意得3m-4=0,且2n-3≠0,解得m=,n≠,
所以当m=,n≠时,该多项式是关于x的二次多项式.
(2)由题意得2n-3=0,2m+5n=0,且3m-4≠0,解得n=,m=-,
所以当n=,m=-时,该多项式是关于x的三次二项式.
10已知多项式:x10-x9y+x8y2-…-xy9+y10.
(1)该多项式有什么特点(规律);
(2)按规律写出多项式的第六项,并指出它的次数和系数;
(3)这个多项式是几次几项式?
解:(1)该多项式的特点是每一项的次数都为10次,每项x的次数在减小,y的次数在增加,且x的次数减小量等于y的次数增加量;当x的次数为偶数时,该项的系数为1,当x的次数为奇数时,该项的系数为-1.
(2)根据规律可得第六项为-x5y5,它的系数是-1,次数是10.
(3)这个多项式是十次十一项式.
同课章节目录
