【精品课】导数综合——不等式证明(共24张PPT)
文档属性
| 名称 | 【精品课】导数综合——不等式证明(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 16:47:50 | ||
图片预览





文档简介
(共24张PPT)
导数综合——不等式证明
x
y
O
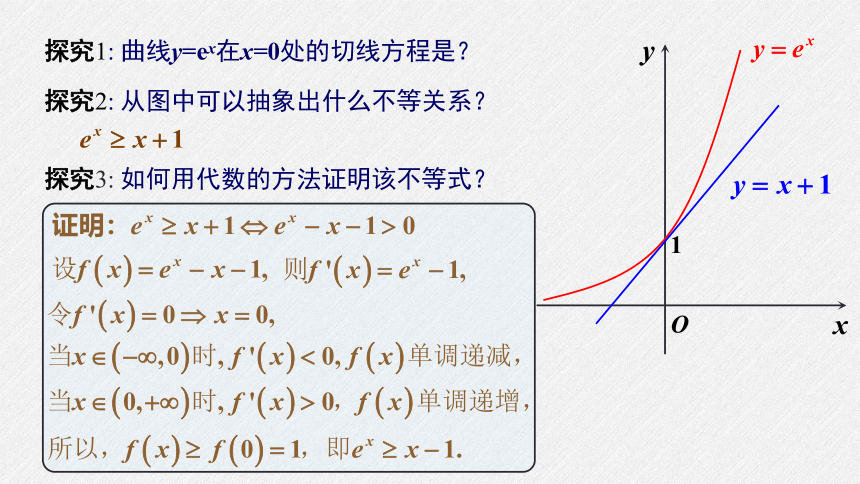
探究1: 曲线y=ex在x=0处的切线方程是?
1
探究2: 从图中可以抽象出什么不等关系?
探究3: 如何用代数的方法证明该不等式?
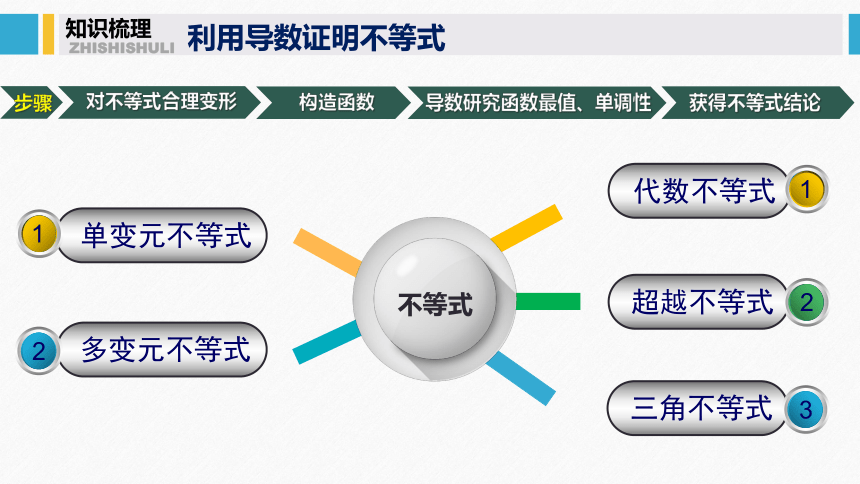
知识梳理
ZHISHISHULI
单变元不等式
1
多变元不等式
2
利用导数证明不等式
代数不等式
1
超越不等式
2
三角不等式
3
不等式
对不等式合理变形
导数研究函数最值、单调性
获得不等式结论
构造函数
步骤
x
y
O
1
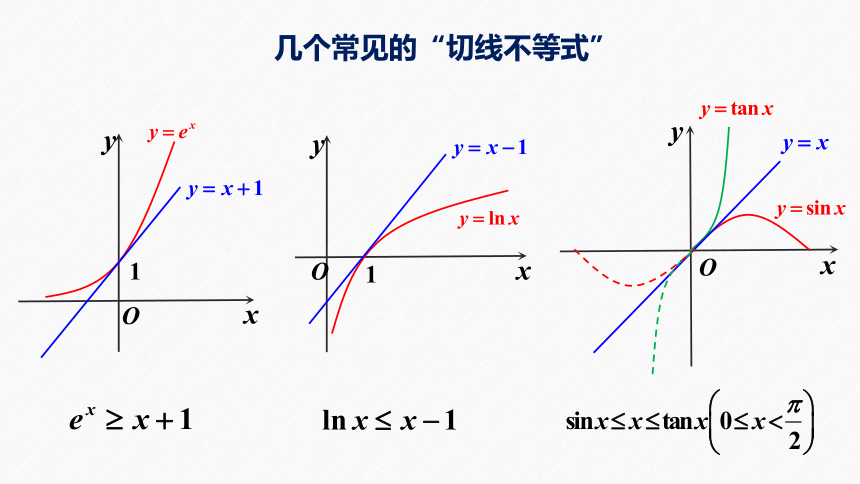
几个常见的“切线不等式”
x
y
O
1
x
y
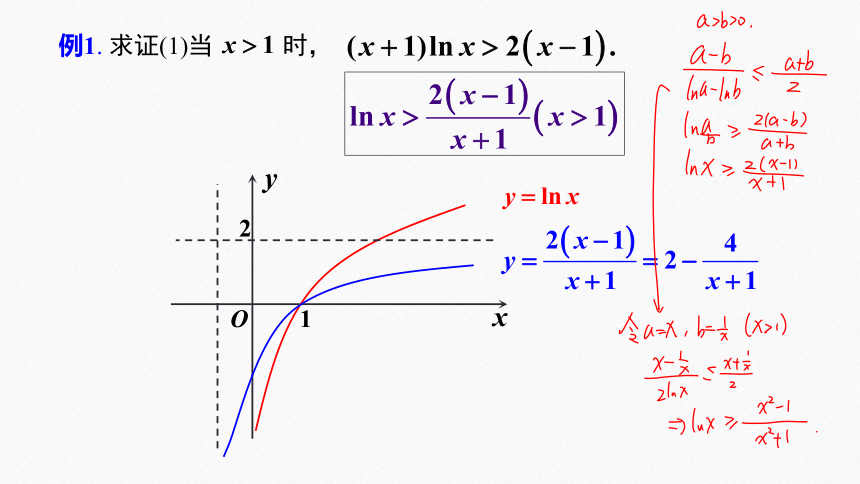
O
例1. 求证(1)当 时,
法一:直接构造函数,两次求导,利用函数单调性证明。
题型演练
TIXINGYANLIAN
2
法二:1.对不等式合理变形后再构造;
2.清理对数的因式再构造可减少求导分析的次数。
例1. 求证(1)当 时,
x
y
O
2
1
例1. 求证(2)
当 时,
方法小结:指数不等式:将变量集中到指数上既可减少求导分析的次数,也可以避免导函数零点不可求。
跟踪训练1 (1 )证明不等式:
放缩后再构造
换元后再构造
(3)已知函数 ,证明: 对任意 恒成立.
分析:
分析:
例2(1)求证:
方法小结:
f(x)>a g(x) h(x)>a g(x)min h(x) min >a.
基于有界性进行分割,构造两个函数
例2. (2)(2016·山东)求证:当 时,
方法小结:基于有界性进行分割,构造两个函数
f(x)>0 g(x)+h(x) >a g(x)min+h(x) min > a.
例2. (2)(2016·山东)求证:当 时,
方法小结
基于有界性进行分割,构造两个函数:(充分不必要条件)
f(x)>0 g(x)+h(x)> a g(x)min+h(x) min > a.
f(x)>a g(x)h(x)>a g(x)min h(x) min >a.(注意先证f(x) ,g(x)的符号)
常见有界函数
几类虚设极值点问题研究指对缠绕难点:指对缠绕想法:指对分离思考:如何分离目标?几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕几类虚设极值点问题研究后续变化二:指对缠绕转化为几个简单类二次函数函数同构几类虚设极值点问题研究后续变化二:指对缠绕很多题均可利用切线放缩,且在切线处取得最值跟踪训练2 (2014·全国Ⅰ)求证:
g(x)min> h(x) max
跟踪训练2 (2014·全国Ⅰ)求证:
放缩法
课堂总结
KETANGZONGJIE
3
变 形
移项、乘除、平方、开方
对数清理因式
指数集中变量
换元
放缩
构 造
一个函数
两个函数
g(x)+h(x)> a
g(x)h(x)>a
化归思想
函数思想
对不等式合理变形
导数研究函数最值、单调性
获得不等式结论
构造函数
步骤
导数综合——不等式证明
x
y
O
探究1: 曲线y=ex在x=0处的切线方程是?
1
探究2: 从图中可以抽象出什么不等关系?
探究3: 如何用代数的方法证明该不等式?
知识梳理
ZHISHISHULI
单变元不等式
1
多变元不等式
2
利用导数证明不等式
代数不等式
1
超越不等式
2
三角不等式
3
不等式
对不等式合理变形
导数研究函数最值、单调性
获得不等式结论
构造函数
步骤
x
y
O
1
几个常见的“切线不等式”
x
y
O
1
x
y
O
例1. 求证(1)当 时,
法一:直接构造函数,两次求导,利用函数单调性证明。
题型演练
TIXINGYANLIAN
2
法二:1.对不等式合理变形后再构造;
2.清理对数的因式再构造可减少求导分析的次数。
例1. 求证(1)当 时,
x
y
O
2
1
例1. 求证(2)
当 时,
方法小结:指数不等式:将变量集中到指数上既可减少求导分析的次数,也可以避免导函数零点不可求。
跟踪训练1 (1 )证明不等式:
放缩后再构造
换元后再构造
(3)已知函数 ,证明: 对任意 恒成立.
分析:
分析:
例2(1)求证:
方法小结:
f(x)>a g(x) h(x)>a g(x)min h(x) min >a.
基于有界性进行分割,构造两个函数
例2. (2)(2016·山东)求证:当 时,
方法小结:基于有界性进行分割,构造两个函数
f(x)>0 g(x)+h(x) >a g(x)min+h(x) min > a.
例2. (2)(2016·山东)求证:当 时,
方法小结
基于有界性进行分割,构造两个函数:(充分不必要条件)
f(x)>0 g(x)+h(x)> a g(x)min+h(x) min > a.
f(x)>a g(x)h(x)>a g(x)min h(x) min >a.(注意先证f(x) ,g(x)的符号)
常见有界函数
几类虚设极值点问题研究指对缠绕难点:指对缠绕想法:指对分离思考:如何分离目标?几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕思考:转化为几个类二次函数模型几类虚设极值点问题研究后续变化二:指对缠绕几类虚设极值点问题研究后续变化二:指对缠绕转化为几个简单类二次函数函数同构几类虚设极值点问题研究后续变化二:指对缠绕很多题均可利用切线放缩,且在切线处取得最值跟踪训练2 (2014·全国Ⅰ)求证:
g(x)min> h(x) max
跟踪训练2 (2014·全国Ⅰ)求证:
放缩法
课堂总结
KETANGZONGJIE
3
变 形
移项、乘除、平方、开方
对数清理因式
指数集中变量
换元
放缩
构 造
一个函数
两个函数
g(x)+h(x)> a
g(x)h(x)>a
化归思想
函数思想
对不等式合理变形
导数研究函数最值、单调性
获得不等式结论
构造函数
步骤
