四川省德阳市第五高级中学2022-2023学年高二上学期9月开学考试数学(文)试题(PDF版含答案)
文档属性
| 名称 | 四川省德阳市第五高级中学2022-2023学年高二上学期9月开学考试数学(文)试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 391.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 00:00:00 | ||
图片预览

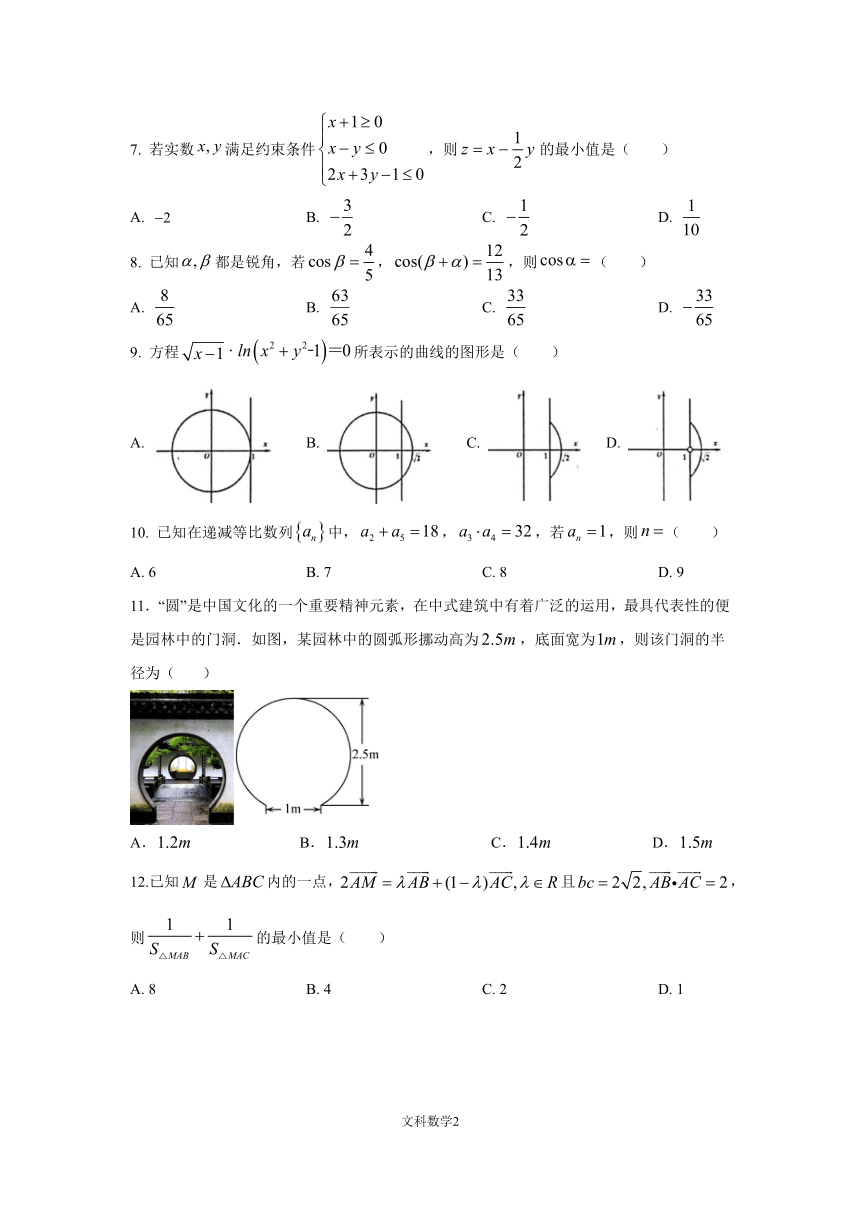


文档简介
德阳五中高 2021级高二上期入学考试
数学试卷(文科)
(总分 150分 答题时间 120分钟)
1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷 1至 12题,
第Ⅱ卷 13——22题,共 150分。
2.答卷前,考生务必将自己的姓名、考号填写在答题卡上。答卷时,考生务必
将答案涂写在答题卷上,答在试卷上的无效。考试结束后,只将答题卷和机读
卡交回。
一.选择题:(每小题 5分,共 60分,在每小题给出的四个选项中,只有一项是
符合要求,请将答案填涂在答题卡上)
x y
1. 直线 1的倾斜角为( )
3 3
2 5
A. B. C. D.
6 3 3 6
2. 已知 sin cos 6 ,则 sin2 的值为( )
2
1
A. 12 B. C.
3 D. 3
2 2 2
x
3. 不等式 0的解集为( )
x 1
A. 1,0 B. 0,1 C. , 1 0, D. ,0 1,
4.若非零实数 a,b满足 a b,则下列不等式一定成立的是( )
1 1
A. B. a b 2 ab C. lg a2 lgb2 D. a3 b3
a b
5. 下列函数中最小值为 4的是( )
4
A. y x2 2x 4 B. y sin x sin x
C. y 2x 22 x D. y ln x
4
ln x
6. 已知直线 l1 : ax y 1 0, l2 : ax (a 2)y 1 0.若 l1 l2 ,则实数a ( )
A. 1或1 B. 0或1 C. 1或2 D. 3或2
文科数学1
x 1 0
7. 若实数 x, y
1
满足约束条件 x y 0 ,则 z x y 的最小值是( )
2
2x 3y 1 0
3 1 1
A. 2 B. C. D.
2 2 10
4 12
8. 已知 , 都是锐角,若 cos , cos( ) ,则 cos ( )
5 13
8 63 33 33
A. B. C. D.
65 65 65 65
9. 方程 x 1 ln x2 y2﹣1 =0所表示的曲线的图形是( )
A. B. C. D.
10. 已知在递减等比数列 an 中, a2 a5 18, a3 a4 32,若 an 1,则 n ( )
A. 6 B. 7 C. 8 D. 9
11.“圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的运用,最具代表性的便
是园林中的门洞.如图,某园林中的圆弧形挪动高为 2.5m,底面宽为1m,则该门洞的半
径为( )
A.1.2m B.1.3m C.1.4m D.1.5m
12.已知M 是 ABC内的一点,2AM AB (1 )AC, R且bc 2 2, AB AC 2,
1 1
则 S 的最小值是( )△MAB S△MAC
A. 8 B. 4 C. 2 D. 1
文科数学2
二.填空题:共 4小题,每小题 5分,共 20分.将答案填在答题卡上.
13. 等差数列 an 中, a3 a4 a5 a6 a7 150,则 a2 a8 ______.
14.已知 ABC是边长为 2的正三角形,D是 AC的中点,则 BD (AB AC ) _____.
15. 若直线 y x b与曲线 y 3 4x x2 有公共点,则b的取值范围是______.
16.在 ABC中,角 A,B,C的对边分别为 a,b,c,若 ac 8, asin B csin 2A 0,则
ABC面积的最大值为______.
三.解答题:解答应写出文字说明、证明过程或演算步骤.
1
17. 已知向量 a 1, a b , a 2b与 a b垂直.3
(1)求 b 的值;
(2)求向量b与 a b夹角的余弦值.
18. 已知 ABC的三个顶点坐标为 A 3,1 ,B 3, 3 ,C 1,7 .
(1)求 BC的中线所在直线方程的一般式方程;
(2)求 ABC的面积.
19. 设函数 f (x) 3 sin 2x cos 2x.
(1)求 f (x)的最小正周期和最值;
(2)已知 a,b,c分别是 ABC内角 A,B,C的对边, f (B) 1, a 4,b 2 7 ,
2BD DA,求线段CD的长.
文科数学3
20.已知数列 an 的前 n项和为 Sn, a1 1,且 Sn 2Sn 1 1 n N*,n 2 .
(1)求 an 的通项公式;
(2)设bn nan,求数列 bn 的前 n项和Tn .
21. 已知以点 A 1,2 为圆心的圆与直线 l1: x 2y 7 0相切,过点B 2,0 的动直线
l与圆 A相交于M 、N 两点,Q是MN的中点.
(1)求圆 A的方程;
(2)当 MN 2 19时,求直线 l的方程.
22. 数学家研究发现,音叉发出的声音(音叉附近空气分子的振动)可以用数学模型
y Asin t 0, t 0 来刻画.1807年,法国数学家傅里叶用一个纯粹的数学定理表述
了任何周期性声音的公式是形如 Asin t 的简单正弦函数之和.若某种声音的模型是函数
f t sin2t t 0 , g t 2 f 2 t af t , t 0 .
7π
(1)求函数 f (t)在 0, 上的值域;
12
7π
(2)若 a 0 ,试研究函数 g(t)在 0, 上的零点个数,并说明理由. 12
文科数学4
德阳五中高 2021 级高二上期入学考试
数学答案(文科)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A D D C C B B D A B A
13. 60 14. 3 15.[1 2 2,3] 16.2
1
17.解:(1)因为 a 1, a b 且a 2b与 a b垂直,3
2
2 2 2 1 2
所以 a 2b a b a a b 2b 0,即 a a b 2 b 0,即12 2 b 0,
3
6
解得 b .
3
2 2 2 2 2
(2) a b a b a 2a b b a 2a b b
2
12 2 1 6 21
3 3
,
3
2
a b 2 2 1 6 b a b b a b b 1,3 3
a b b
cos 1 3 14
a b b 21 6 14
设向量b与 a b的夹角为 ,所以 3 3 .
3 1
x 2
18.解(1)设 BC的中点D x, y 2,则 ,即D 2,2 .
y 3 7 2
2
k 2 1 1AD 2 3 5,
1
所以 BC的中线所在直线方程为 y 2 x 2 ,即 x 5y 8 0 .
5
7 1 3 3 1 2
(2) kAC k 1 3 2, AB 3 3 3,
所以 kAC kAB 1,即 AC AB .
AC 1 3 2 7 1 2 2 13 2, AB 3 3 3 1 2 2 13,
所以 S 1△ABC 2 13 2 13 26 .2
19.解(1)∵ f (x) 3 sin 2x cos 2x
3
2 sin 2x
1
cos 2x
2 2
2sin 2x
6
,
2
∴T ,∴ f (x)
2 max
2, f (x)min 2;
(2)
∵ f (B) 2sin 2B
1, B (0, )
,∴ B ,
6 3
∵b2 a2 c2 2accosB,
∴ c2 4c 12 0,
∴ c 6( c 2舍).
1
∵ 2BD DA,∴ BD c 2,3
∴CD2 42 22 2 4 2cos 12,
3
∴CD 2 3;
综上, f x 的周期为 ,最大值为 2,最小值为-2,CD 2 3 .
20.(1)解法一:因为 Sn 2S
*
n 1 1 n N ,n 2 ①,
所以 Sn 1 2Sn 1②,
② ①得 Sn 1 Sn 2Sn 1 2Sn 1 1 即 an 1 2an,
a3 a 4
a
所以
5 2
a a a ,2 3 4
a
又当 n 2 S 2时, 2 2S1 1,又 a1 1,所以 a2 2,所以 2a ,1
an 1
所以 2(n N
*)
a ,所以数列{an}是以1为首项, 2为公比的等比数列,n
所以 an = 2
n-1
.
解法二: n 2时,Sn 2Sn 1 1 Sn 1 2(Sn 1 1)
S1 1 2 0 {Sn 1}是以2为首项,2为公比的等比数列
Sn 1 2 2
n 1 2n Sn 2
n 1
n 2 a S S 2n 2n 1当 时, n n n 1 2
n 1
a 1 a 2n 1(n N*由 1 n )
(2)解:由(1)可得bn na n 2
n 1
n ,
T 1 20 2 21 2 3 1所以 n 3 2 4 2 (n 1) ( )
n 2 n 2n 1,
2
则 2Tn 1 2
1 2 22 3 23 4 24 (n 1) 2n 1 n 2n
n
两式相减得, Tn 2
0 21 22 23 2n 1 n 2n 1 2 n 2n 1 (n 1) 2n
1 2
n
所以Tn (n 1) 2 1.
21.解(1)设圆 A的半径为 R,由于圆 A与直线 l1 : x 2y 7 0相切,
R | 1 4 7 | 2 5,
5
圆 A的方程为 (x 1)2 (y 2)2 20;
(2)①当直线 l与 x轴垂直时,易知 x 2符合题意;
②当直线 l与 x轴不垂直时,
设直线 l的方程为y k(x 2),即 kx y 2k 0,
连接 AQ,则 AQ MN
|MN | 2 19 , | AQ | 20 19 1,
则由 | AQ |
| k 2 |
1 3
2 ,得 k , 直线 l : 3x 4y 6 0.1 k 4
故直线 l的方程为 x 2或3x 4y 6 0 .
7 7
22.解:(1)因为 t 0, π ,所以 2t 12
0, π ,
6
所以 sin 7π sin2t sin π 1,即 sin2t 1,
6 2 2
7 1
所以函数 f (t)在 0, π 上的值域为 12 ,1 . 2
a
(2)因为 2 f 2 (t) af (t) 0,所以 f (t) f (t) 0.
2
①当 a 0 时, f (t) 0,因为 2t 0, 7 π π ,所以 2t π,解得 t , 6 2
g(t) 7 所以 在 0, π 上只有一个零点. 12
②当 a 0 时, f (t) 0或 f (t) a .令 u 2u2 au,u 1
2
,1 ,则 2
a 1 min
a ,1 b u 1ⅰ若 ,记 则 在 ,b 1上单调递减,且 2 0, b 0, 4 2 2
所以 f (t) 0 π 7 ,由①得 t ,所以 g(t)在 0, π 上只有一个零点.2 12
a u 1 , a a ,1 1 ⅱ若 1 ,则 在 上单调递减,在 上单调递增,且 0, 1 0,2 2 4 4 2
所以 f (t) 0 π 7,由①得 t f (t) 1 2t π; ,因为 0, π ,所以 2t ,解得 t
π
;
2 6 2 4
所以 g(t) 在 0, 7 π 上有两个零点. 12
a 1 u 1 a , a 1 ⅲ若 ,则 在 上单调递减,在 ,1 上单调递增,且 0, 1 0,2 2 4 4 2
f (t) 0 π π,由①得 t ; f (t) a 0,1 ,当 t 0,
时,令 h(t) sin 2t
a
,t 7
2 2 2 2
0, π ,
12
h(π) sin 2t a 1 a 0,h( 7π则 ) sin 2t
a 1 a
0 ,根据零点存在定理,
4 2 2 12 2 2 2
h t π , 7π 所以连续函数 在 上存在零点, 4 12
π 7π π 7π
因为 h t 在 , 上单调递减,所以连续函数 h t 在 , 上只有一个零点. 4 12 4 12
同理,连续函数 h t 在 0,
π
上只有一个零点. 4
所以 g(t) 在 0, 7 π 上有三个零点. 12
7
综上,当 a 0 或 a 2 时, g(t)在 0, π 上只有一个零点; 12
当 a 2 时, g(t) 在 0, 7 π 上有两个零点; 12
7
当 012
数学试卷(文科)
(总分 150分 答题时间 120分钟)
1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷 1至 12题,
第Ⅱ卷 13——22题,共 150分。
2.答卷前,考生务必将自己的姓名、考号填写在答题卡上。答卷时,考生务必
将答案涂写在答题卷上,答在试卷上的无效。考试结束后,只将答题卷和机读
卡交回。
一.选择题:(每小题 5分,共 60分,在每小题给出的四个选项中,只有一项是
符合要求,请将答案填涂在答题卡上)
x y
1. 直线 1的倾斜角为( )
3 3
2 5
A. B. C. D.
6 3 3 6
2. 已知 sin cos 6 ,则 sin2 的值为( )
2
1
A. 12 B. C.
3 D. 3
2 2 2
x
3. 不等式 0的解集为( )
x 1
A. 1,0 B. 0,1 C. , 1 0, D. ,0 1,
4.若非零实数 a,b满足 a b,则下列不等式一定成立的是( )
1 1
A. B. a b 2 ab C. lg a2 lgb2 D. a3 b3
a b
5. 下列函数中最小值为 4的是( )
4
A. y x2 2x 4 B. y sin x sin x
C. y 2x 22 x D. y ln x
4
ln x
6. 已知直线 l1 : ax y 1 0, l2 : ax (a 2)y 1 0.若 l1 l2 ,则实数a ( )
A. 1或1 B. 0或1 C. 1或2 D. 3或2
文科数学1
x 1 0
7. 若实数 x, y
1
满足约束条件 x y 0 ,则 z x y 的最小值是( )
2
2x 3y 1 0
3 1 1
A. 2 B. C. D.
2 2 10
4 12
8. 已知 , 都是锐角,若 cos , cos( ) ,则 cos ( )
5 13
8 63 33 33
A. B. C. D.
65 65 65 65
9. 方程 x 1 ln x2 y2﹣1 =0所表示的曲线的图形是( )
A. B. C. D.
10. 已知在递减等比数列 an 中, a2 a5 18, a3 a4 32,若 an 1,则 n ( )
A. 6 B. 7 C. 8 D. 9
11.“圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的运用,最具代表性的便
是园林中的门洞.如图,某园林中的圆弧形挪动高为 2.5m,底面宽为1m,则该门洞的半
径为( )
A.1.2m B.1.3m C.1.4m D.1.5m
12.已知M 是 ABC内的一点,2AM AB (1 )AC, R且bc 2 2, AB AC 2,
1 1
则 S 的最小值是( )△MAB S△MAC
A. 8 B. 4 C. 2 D. 1
文科数学2
二.填空题:共 4小题,每小题 5分,共 20分.将答案填在答题卡上.
13. 等差数列 an 中, a3 a4 a5 a6 a7 150,则 a2 a8 ______.
14.已知 ABC是边长为 2的正三角形,D是 AC的中点,则 BD (AB AC ) _____.
15. 若直线 y x b与曲线 y 3 4x x2 有公共点,则b的取值范围是______.
16.在 ABC中,角 A,B,C的对边分别为 a,b,c,若 ac 8, asin B csin 2A 0,则
ABC面积的最大值为______.
三.解答题:解答应写出文字说明、证明过程或演算步骤.
1
17. 已知向量 a 1, a b , a 2b与 a b垂直.3
(1)求 b 的值;
(2)求向量b与 a b夹角的余弦值.
18. 已知 ABC的三个顶点坐标为 A 3,1 ,B 3, 3 ,C 1,7 .
(1)求 BC的中线所在直线方程的一般式方程;
(2)求 ABC的面积.
19. 设函数 f (x) 3 sin 2x cos 2x.
(1)求 f (x)的最小正周期和最值;
(2)已知 a,b,c分别是 ABC内角 A,B,C的对边, f (B) 1, a 4,b 2 7 ,
2BD DA,求线段CD的长.
文科数学3
20.已知数列 an 的前 n项和为 Sn, a1 1,且 Sn 2Sn 1 1 n N*,n 2 .
(1)求 an 的通项公式;
(2)设bn nan,求数列 bn 的前 n项和Tn .
21. 已知以点 A 1,2 为圆心的圆与直线 l1: x 2y 7 0相切,过点B 2,0 的动直线
l与圆 A相交于M 、N 两点,Q是MN的中点.
(1)求圆 A的方程;
(2)当 MN 2 19时,求直线 l的方程.
22. 数学家研究发现,音叉发出的声音(音叉附近空气分子的振动)可以用数学模型
y Asin t 0, t 0 来刻画.1807年,法国数学家傅里叶用一个纯粹的数学定理表述
了任何周期性声音的公式是形如 Asin t 的简单正弦函数之和.若某种声音的模型是函数
f t sin2t t 0 , g t 2 f 2 t af t , t 0 .
7π
(1)求函数 f (t)在 0, 上的值域;
12
7π
(2)若 a 0 ,试研究函数 g(t)在 0, 上的零点个数,并说明理由. 12
文科数学4
德阳五中高 2021 级高二上期入学考试
数学答案(文科)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A D D C C B B D A B A
13. 60 14. 3 15.[1 2 2,3] 16.2
1
17.解:(1)因为 a 1, a b 且a 2b与 a b垂直,3
2
2 2 2 1 2
所以 a 2b a b a a b 2b 0,即 a a b 2 b 0,即12 2 b 0,
3
6
解得 b .
3
2 2 2 2 2
(2) a b a b a 2a b b a 2a b b
2
12 2 1 6 21
3 3
,
3
2
a b 2 2 1 6 b a b b a b b 1,3 3
a b b
cos 1 3 14
a b b 21 6 14
设向量b与 a b的夹角为 ,所以 3 3 .
3 1
x 2
18.解(1)设 BC的中点D x, y 2,则 ,即D 2,2 .
y 3 7 2
2
k 2 1 1AD 2 3 5,
1
所以 BC的中线所在直线方程为 y 2 x 2 ,即 x 5y 8 0 .
5
7 1 3 3 1 2
(2) kAC k 1 3 2, AB 3 3 3,
所以 kAC kAB 1,即 AC AB .
AC 1 3 2 7 1 2 2 13 2, AB 3 3 3 1 2 2 13,
所以 S 1△ABC 2 13 2 13 26 .2
19.解(1)∵ f (x) 3 sin 2x cos 2x
3
2 sin 2x
1
cos 2x
2 2
2sin 2x
6
,
2
∴T ,∴ f (x)
2 max
2, f (x)min 2;
(2)
∵ f (B) 2sin 2B
1, B (0, )
,∴ B ,
6 3
∵b2 a2 c2 2accosB,
∴ c2 4c 12 0,
∴ c 6( c 2舍).
1
∵ 2BD DA,∴ BD c 2,3
∴CD2 42 22 2 4 2cos 12,
3
∴CD 2 3;
综上, f x 的周期为 ,最大值为 2,最小值为-2,CD 2 3 .
20.(1)解法一:因为 Sn 2S
*
n 1 1 n N ,n 2 ①,
所以 Sn 1 2Sn 1②,
② ①得 Sn 1 Sn 2Sn 1 2Sn 1 1 即 an 1 2an,
a3 a 4
a
所以
5 2
a a a ,2 3 4
a
又当 n 2 S 2时, 2 2S1 1,又 a1 1,所以 a2 2,所以 2a ,1
an 1
所以 2(n N
*)
a ,所以数列{an}是以1为首项, 2为公比的等比数列,n
所以 an = 2
n-1
.
解法二: n 2时,Sn 2Sn 1 1 Sn 1 2(Sn 1 1)
S1 1 2 0 {Sn 1}是以2为首项,2为公比的等比数列
Sn 1 2 2
n 1 2n Sn 2
n 1
n 2 a S S 2n 2n 1当 时, n n n 1 2
n 1
a 1 a 2n 1(n N*由 1 n )
(2)解:由(1)可得bn na n 2
n 1
n ,
T 1 20 2 21 2 3 1所以 n 3 2 4 2 (n 1) ( )
n 2 n 2n 1,
2
则 2Tn 1 2
1 2 22 3 23 4 24 (n 1) 2n 1 n 2n
n
两式相减得, Tn 2
0 21 22 23 2n 1 n 2n 1 2 n 2n 1 (n 1) 2n
1 2
n
所以Tn (n 1) 2 1.
21.解(1)设圆 A的半径为 R,由于圆 A与直线 l1 : x 2y 7 0相切,
R | 1 4 7 | 2 5,
5
圆 A的方程为 (x 1)2 (y 2)2 20;
(2)①当直线 l与 x轴垂直时,易知 x 2符合题意;
②当直线 l与 x轴不垂直时,
设直线 l的方程为y k(x 2),即 kx y 2k 0,
连接 AQ,则 AQ MN
|MN | 2 19 , | AQ | 20 19 1,
则由 | AQ |
| k 2 |
1 3
2 ,得 k , 直线 l : 3x 4y 6 0.1 k 4
故直线 l的方程为 x 2或3x 4y 6 0 .
7 7
22.解:(1)因为 t 0, π ,所以 2t 12
0, π ,
6
所以 sin 7π sin2t sin π 1,即 sin2t 1,
6 2 2
7 1
所以函数 f (t)在 0, π 上的值域为 12 ,1 . 2
a
(2)因为 2 f 2 (t) af (t) 0,所以 f (t) f (t) 0.
2
①当 a 0 时, f (t) 0,因为 2t 0, 7 π π ,所以 2t π,解得 t , 6 2
g(t) 7 所以 在 0, π 上只有一个零点. 12
②当 a 0 时, f (t) 0或 f (t) a .令 u 2u2 au,u 1
2
,1 ,则 2
a 1 min
a ,1 b u 1ⅰ若 ,记 则 在 ,b 1上单调递减,且 2 0, b 0, 4 2 2
所以 f (t) 0 π 7 ,由①得 t ,所以 g(t)在 0, π 上只有一个零点.2 12
a u 1 , a a ,1 1 ⅱ若 1 ,则 在 上单调递减,在 上单调递增,且 0, 1 0,2 2 4 4 2
所以 f (t) 0 π 7,由①得 t f (t) 1 2t π; ,因为 0, π ,所以 2t ,解得 t
π
;
2 6 2 4
所以 g(t) 在 0, 7 π 上有两个零点. 12
a 1 u 1 a , a 1 ⅲ若 ,则 在 上单调递减,在 ,1 上单调递增,且 0, 1 0,2 2 4 4 2
f (t) 0 π π,由①得 t ; f (t) a 0,1 ,当 t 0,
时,令 h(t) sin 2t
a
,t 7
2 2 2 2
0, π ,
12
h(π) sin 2t a 1 a 0,h( 7π则 ) sin 2t
a 1 a
0 ,根据零点存在定理,
4 2 2 12 2 2 2
h t π , 7π 所以连续函数 在 上存在零点, 4 12
π 7π π 7π
因为 h t 在 , 上单调递减,所以连续函数 h t 在 , 上只有一个零点. 4 12 4 12
同理,连续函数 h t 在 0,
π
上只有一个零点. 4
所以 g(t) 在 0, 7 π 上有三个零点. 12
7
综上,当 a 0 或 a 2 时, g(t)在 0, π 上只有一个零点; 12
当 a 2 时, g(t) 在 0, 7 π 上有两个零点; 12
7
当 0
同课章节目录
