2022—2023学年湘教版数学 七年级上册3.4 第1课时 用一次方程模型解决实际问题的步骤 课件(共25张PPT)
文档属性
| 名称 | 2022—2023学年湘教版数学 七年级上册3.4 第1课时 用一次方程模型解决实际问题的步骤 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 412.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 12:55:40 | ||
图片预览








文档简介
(共25张PPT)
第三章 一元一次方程
3.4 一元一次方程模型的应用
第1课时 用一次方程模型解决实际问题的步骤
根据实际问题中的数量关系,能利用一元一次方程解决和差问题.
◎重点:利用一元一次方程解决和差倍分问题.
◎难点:找等量关系.
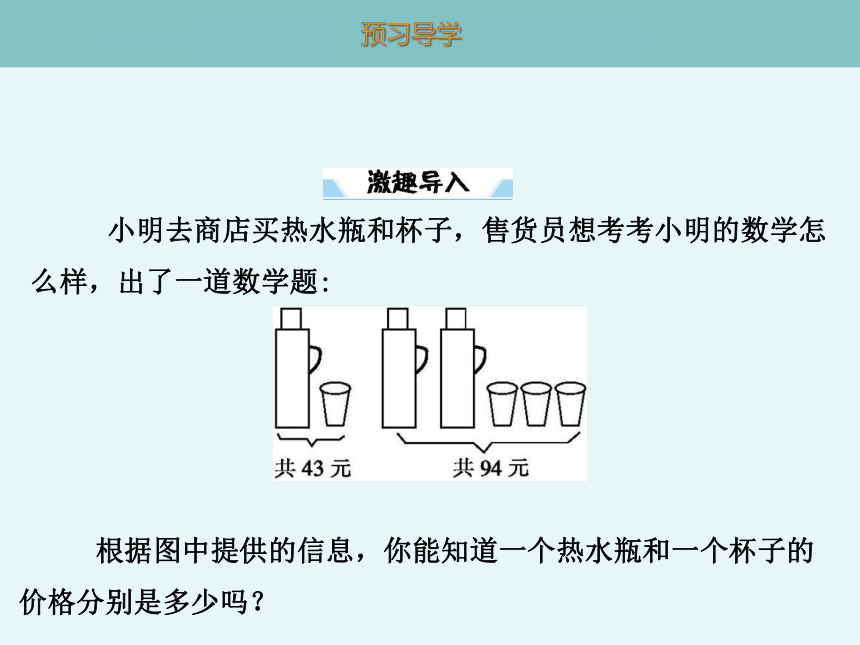
小明去商店买热水瓶和杯子,售货员想考考小明的数学怎么样,出了一道数学题:
根据图中提供的信息,你能知道一个热水瓶和一个杯子的价格分别是多少吗?
列一元一次方程解决和差倍分问题
阅读课本本课时“动脑筋”内容,思考:
1.题中的已知量是: 单价、门票总数量、总票款 ,未知量是 全价票和半价票售出数量 .
2.本题的等量关系是 全价票款+半价票款=总票款 .
3.如果设半价票是x张,则全价票是 (1200-x) 张,根据题意可列方程: 20x+10(1200-x)=20000 .
4.请同学们解所列的方程.
单价、门票总数量、总票款
全价票和半价票售出数量
全价票款+半价票款=总票款
(1200-x)
20x+10(1200-x)=20000
1.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元.如果设水性笔的单价为x元,那么下列所列方程正确的是 ( A )
A.5(x-2)+3x=14
B.5(x+2)+3x=14
C.5x+3(x+2)=14
D.5x+3(x-2)=14
A
2.有若干只鸡和兔关在一个笼子里,从上面数,有30个头;从下面数,有84条腿,问笼中各有几只鸡和兔?
解:设有鸡x只,则兔有(30-x)只,
依题意有2x+4(30-x)=84,解得x=18,30-18=12.
答:有鸡18只,兔12只.
归纳总结 和、差、倍、分问题常常通过“几倍、多、少、差、几分之几”等关键词体现出来,设未知数时常设其中一个量,将另一个量用未知数表示出来.
列一元一次方程解决实际问题的步骤
阅读课本“议一议”填空:
运用一元一次方程解决实际问题的步骤是:实际问题, 设未知数 ,列方程, 解方程 ,检验.
设
未知数
解方程
归纳总结 列一元一次方程解决实际问题时要注意:①明确题目类别,并明确该类问题中有几类不同性质的量,它们之间的基本关系式是什么.例如行程问题中有三类不同性质的量,速度、时间、路程,它们之间的数量基本关系是,速度×时间=路程.②要认真审查已知数量与未知数量的性质,同类性质的量有几种,已知量及未知量之间的对应关系.必要时,可以通过列表格,画线段图等办法对已知数量及未知数量的关系进行整理.③正确地用含有x的代数式表示相等关系中的有关未知量是列方程的基础.一般地,经过上述分析,有助于找到相等关系,列出方程.
利用一元一次方程解决劳力调配问题
1.在甲处劳动的有27人,在乙处劳动的有19人,现调20人去支援,使甲处人数为乙处人数的2倍,应调往甲、乙两处各多少人?
解:设从20人中调往甲处x人,那么调往乙处是(20-x)人,根据题意,得27+x=2[19+(20-x)],
解得x=17,当x=17时,20-x=3.
答:应调往甲处17人,乙处3人.
思考以下两个问题:(1)若设从20人中调往甲处x人,那么调往乙处有多少人?(2)本题的等量关系是什么?
答:(1)(20-x)人.
(2)调人后甲处人数=2×调人后乙处的人数.
变式训练 小明想从“天猫”某网店购买计算器,经查询,某品牌A型号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A、B两种型号计算器的单价分别是多少?
解:设A型号计算器的单价为x元,B型号计算器的单价为(x-10)元,依题意得5x=7(x-10),解得x=35,所以x-10=25.
答:A、B两种型号计算器的单价分别是35元和25元.
间接设未知数
2.全班同学划船,如果减少一条船,每条船正好坐10个同学,如果增加一条船,每条船正好坐8个同学,问这个班有多少个同学?
解:设有x条船,则有10(x-1)=8(x+1),解得x=9,则有学生10(9-1)=80(人).
答:这个班有学生80人.
变式训练 奶奶用20元钱买了2斤桔子、3斤苹果、4斤海棠,已知桔子、苹果、海棠的单价比是1∶2∶3,问各买6斤共要多少钱?
解:设桔子、苹果、海棠的单价分别为x元/斤、2x元/斤、3x元/斤,则有2x+3×2x+4×3x=20,解得x=1,所以各买6斤共要1×6+2×6+3×6=36(元).
答:各买6斤共要36元.
方法归纳交流 列方程解应用题时,我们习惯于题目中求什么就设什么,即 直接 设未知数.但有些问题用这种方法处理会非常麻烦,有必要 间接 设未知数,给解题带来方便.
直接
间接
1为做好疫情防控工作,学校把一批口罩分给值班人员,如果每人分3个,那么剩余20个;如果每人分4个,那么还缺25个.设值班人员有x人,下列方程正确的是 ( A )
A.3x+20=4x-25
B.3x-25=4x+20
C.4x-3x=25-20
D.3x-20=4x+25
A
2学校机房今年和去年共购置了100台计算机,已知今年购置计算机的数量是去年购置计算机数量的3倍,则今年购置计算机的数量是 ( C )
A.25台 B.50台 C.75台 D.100台
3用一根长为10 m的铁丝围成一个长方形,若长方形的长比宽多1.4 m,则此时长方形的长为 3.2 m,宽为 1.8 m.
C
3.2
1.8
4某商店经销甲、乙两种商品.现有如下信息:
请根据以上信息,求甲、乙两种商品的零售单价.
解:设甲的进货单价为x元,则乙的进货单价为(3-x)元,由题意得3(x+1)+2(5-2x)=12,解得x=1,1+x=2,5-2x=3.
答:甲的零售单价为2元,乙的零售单价为3元.
5某洗衣机厂计划生产25500台洗衣机,其中A、B、C三种型号的洗衣机的数量比为1∶2∶14,这三种洗衣机计划各生产多少台?
解:设A、B、C三种型号的洗衣机分别为x台,2x台,14x台,由题意得x+2x+14x=25500,解得x=1500,1500×2=3000(台),1500×14=21000(台).
答:A、B、C三种洗衣机计划各生产1500台,3000台和21000台.
6为举办校园文化艺术节,甲、乙两班准备给合唱的每位同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 第1套至 45套 第46套至 90套 第91套
及以上
每套服装的价格 60元 50元 40元
如果两班单独给每位同学购买一套服装,那么一共应付5450元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比两班单独购买可以节省多少钱?
(2)问甲、乙两班各有多少名同学?
解:(1)由题意,得5450-45×60+(90-45)×50+(92-90)×40=5450-5030=420(元),即两班联合起来购买服装比各自购买服装共可以节省420元.
(2)设甲班有x名学生准备参加演出(依题意46<x<90),则乙班有学生(92-x)人.依题意得45×60+50(x-45)+60(92-x)=5450,解得x=52.于是92-x=40(人).
答:甲班有52人,乙班有40人.
7某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗,为什么?
解:(1)设售出成人票x张,则售出学生票(1000-x)张,根据题意列方程得,
8x+5(1000-x)=6920,解得x=640,则1000-x=360(张).
答:共售出成人票640张,学生票360张.
(2)设售出成人票x张,则售出学生票(1000-x)张,
根据题意列方程得,8x+5(1000-x)=7290,解得x=763.33333.因为票都是整张卖的,必须是正整数,所以所得的票款不可能是7290元.
8某公园停车场的收费标准如下:小型汽车的停车费为10元/辆,中型汽车的停车费为15元/辆.某天该停车场有小、中型汽车共68辆,设中型汽车有x辆.
(1)求小型汽车的车辆数.(用含x的代数式表示)
(2)这天这些车共缴纳停车费710元,求小、中型汽车各有多少辆.
解:(1)小型汽车的车辆数为(68-x).
(2)小型汽车共缴纳停车费10(68-x)元,中型汽车共缴纳停车费15x元,
根据题意可列方程10(68-x)+15x=710,解得x=6.
所以68-x=68-6=62(辆).
答:小型汽车有62辆,中型汽车有6辆.
第三章 一元一次方程
3.4 一元一次方程模型的应用
第1课时 用一次方程模型解决实际问题的步骤
根据实际问题中的数量关系,能利用一元一次方程解决和差问题.
◎重点:利用一元一次方程解决和差倍分问题.
◎难点:找等量关系.
小明去商店买热水瓶和杯子,售货员想考考小明的数学怎么样,出了一道数学题:
根据图中提供的信息,你能知道一个热水瓶和一个杯子的价格分别是多少吗?
列一元一次方程解决和差倍分问题
阅读课本本课时“动脑筋”内容,思考:
1.题中的已知量是: 单价、门票总数量、总票款 ,未知量是 全价票和半价票售出数量 .
2.本题的等量关系是 全价票款+半价票款=总票款 .
3.如果设半价票是x张,则全价票是 (1200-x) 张,根据题意可列方程: 20x+10(1200-x)=20000 .
4.请同学们解所列的方程.
单价、门票总数量、总票款
全价票和半价票售出数量
全价票款+半价票款=总票款
(1200-x)
20x+10(1200-x)=20000
1.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元.如果设水性笔的单价为x元,那么下列所列方程正确的是 ( A )
A.5(x-2)+3x=14
B.5(x+2)+3x=14
C.5x+3(x+2)=14
D.5x+3(x-2)=14
A
2.有若干只鸡和兔关在一个笼子里,从上面数,有30个头;从下面数,有84条腿,问笼中各有几只鸡和兔?
解:设有鸡x只,则兔有(30-x)只,
依题意有2x+4(30-x)=84,解得x=18,30-18=12.
答:有鸡18只,兔12只.
归纳总结 和、差、倍、分问题常常通过“几倍、多、少、差、几分之几”等关键词体现出来,设未知数时常设其中一个量,将另一个量用未知数表示出来.
列一元一次方程解决实际问题的步骤
阅读课本“议一议”填空:
运用一元一次方程解决实际问题的步骤是:实际问题, 设未知数 ,列方程, 解方程 ,检验.
设
未知数
解方程
归纳总结 列一元一次方程解决实际问题时要注意:①明确题目类别,并明确该类问题中有几类不同性质的量,它们之间的基本关系式是什么.例如行程问题中有三类不同性质的量,速度、时间、路程,它们之间的数量基本关系是,速度×时间=路程.②要认真审查已知数量与未知数量的性质,同类性质的量有几种,已知量及未知量之间的对应关系.必要时,可以通过列表格,画线段图等办法对已知数量及未知数量的关系进行整理.③正确地用含有x的代数式表示相等关系中的有关未知量是列方程的基础.一般地,经过上述分析,有助于找到相等关系,列出方程.
利用一元一次方程解决劳力调配问题
1.在甲处劳动的有27人,在乙处劳动的有19人,现调20人去支援,使甲处人数为乙处人数的2倍,应调往甲、乙两处各多少人?
解:设从20人中调往甲处x人,那么调往乙处是(20-x)人,根据题意,得27+x=2[19+(20-x)],
解得x=17,当x=17时,20-x=3.
答:应调往甲处17人,乙处3人.
思考以下两个问题:(1)若设从20人中调往甲处x人,那么调往乙处有多少人?(2)本题的等量关系是什么?
答:(1)(20-x)人.
(2)调人后甲处人数=2×调人后乙处的人数.
变式训练 小明想从“天猫”某网店购买计算器,经查询,某品牌A型号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A、B两种型号计算器的单价分别是多少?
解:设A型号计算器的单价为x元,B型号计算器的单价为(x-10)元,依题意得5x=7(x-10),解得x=35,所以x-10=25.
答:A、B两种型号计算器的单价分别是35元和25元.
间接设未知数
2.全班同学划船,如果减少一条船,每条船正好坐10个同学,如果增加一条船,每条船正好坐8个同学,问这个班有多少个同学?
解:设有x条船,则有10(x-1)=8(x+1),解得x=9,则有学生10(9-1)=80(人).
答:这个班有学生80人.
变式训练 奶奶用20元钱买了2斤桔子、3斤苹果、4斤海棠,已知桔子、苹果、海棠的单价比是1∶2∶3,问各买6斤共要多少钱?
解:设桔子、苹果、海棠的单价分别为x元/斤、2x元/斤、3x元/斤,则有2x+3×2x+4×3x=20,解得x=1,所以各买6斤共要1×6+2×6+3×6=36(元).
答:各买6斤共要36元.
方法归纳交流 列方程解应用题时,我们习惯于题目中求什么就设什么,即 直接 设未知数.但有些问题用这种方法处理会非常麻烦,有必要 间接 设未知数,给解题带来方便.
直接
间接
1为做好疫情防控工作,学校把一批口罩分给值班人员,如果每人分3个,那么剩余20个;如果每人分4个,那么还缺25个.设值班人员有x人,下列方程正确的是 ( A )
A.3x+20=4x-25
B.3x-25=4x+20
C.4x-3x=25-20
D.3x-20=4x+25
A
2学校机房今年和去年共购置了100台计算机,已知今年购置计算机的数量是去年购置计算机数量的3倍,则今年购置计算机的数量是 ( C )
A.25台 B.50台 C.75台 D.100台
3用一根长为10 m的铁丝围成一个长方形,若长方形的长比宽多1.4 m,则此时长方形的长为 3.2 m,宽为 1.8 m.
C
3.2
1.8
4某商店经销甲、乙两种商品.现有如下信息:
请根据以上信息,求甲、乙两种商品的零售单价.
解:设甲的进货单价为x元,则乙的进货单价为(3-x)元,由题意得3(x+1)+2(5-2x)=12,解得x=1,1+x=2,5-2x=3.
答:甲的零售单价为2元,乙的零售单价为3元.
5某洗衣机厂计划生产25500台洗衣机,其中A、B、C三种型号的洗衣机的数量比为1∶2∶14,这三种洗衣机计划各生产多少台?
解:设A、B、C三种型号的洗衣机分别为x台,2x台,14x台,由题意得x+2x+14x=25500,解得x=1500,1500×2=3000(台),1500×14=21000(台).
答:A、B、C三种洗衣机计划各生产1500台,3000台和21000台.
6为举办校园文化艺术节,甲、乙两班准备给合唱的每位同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 第1套至 45套 第46套至 90套 第91套
及以上
每套服装的价格 60元 50元 40元
如果两班单独给每位同学购买一套服装,那么一共应付5450元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比两班单独购买可以节省多少钱?
(2)问甲、乙两班各有多少名同学?
解:(1)由题意,得5450-45×60+(90-45)×50+(92-90)×40=5450-5030=420(元),即两班联合起来购买服装比各自购买服装共可以节省420元.
(2)设甲班有x名学生准备参加演出(依题意46<x<90),则乙班有学生(92-x)人.依题意得45×60+50(x-45)+60(92-x)=5450,解得x=52.于是92-x=40(人).
答:甲班有52人,乙班有40人.
7某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗,为什么?
解:(1)设售出成人票x张,则售出学生票(1000-x)张,根据题意列方程得,
8x+5(1000-x)=6920,解得x=640,则1000-x=360(张).
答:共售出成人票640张,学生票360张.
(2)设售出成人票x张,则售出学生票(1000-x)张,
根据题意列方程得,8x+5(1000-x)=7290,解得x=763.33333.因为票都是整张卖的,必须是正整数,所以所得的票款不可能是7290元.
8某公园停车场的收费标准如下:小型汽车的停车费为10元/辆,中型汽车的停车费为15元/辆.某天该停车场有小、中型汽车共68辆,设中型汽车有x辆.
(1)求小型汽车的车辆数.(用含x的代数式表示)
(2)这天这些车共缴纳停车费710元,求小、中型汽车各有多少辆.
解:(1)小型汽车的车辆数为(68-x).
(2)小型汽车共缴纳停车费10(68-x)元,中型汽车共缴纳停车费15x元,
根据题意可列方程10(68-x)+15x=710,解得x=6.
所以68-x=68-6=62(辆).
答:小型汽车有62辆,中型汽车有6辆.
同课章节目录
