湘教版九年级数学上册第1章反比例函数题型分类综合练习题 (含解析)
文档属性
| 名称 | 湘教版九年级数学上册第1章反比例函数题型分类综合练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 13:07:06 | ||
图片预览



文档简介
2022-2023学年湘教版九年级数学上册《第1章反比例函数》题型分类综合练习题(附答案)
一.反比例函数的定义
1.如图用方砖铺地时,若地面很大,而方砖的数量有限,当铺成的地面为长方形时,长方形的宽x与长y成 关系.
2.已知变量y与变量x之间的对应值如下表:
x … 1 2 3 4 5 6 …
y … 6 3 2 1.5 1.2 1 …
试求出变量y与x之间的函数关系式: .
3.已知函数,当k= 时,y是x的反比例函数.
二.反比例函数的图象
4.已知关于x的函数y=k(x+1)和,它们在同一坐标系中的图象大致是( )
A. B.
C. D.
5.如图是三个反比例函数的图象的分支,其中k1,k2,k3的大小关系是( )
A.k1>k2>k3 B.k1<k2<k3 C.k2>k3>k1 D.k1=k2>k3
6.函数的图象如图所示,下列对该函数性质的论断正确的是
(1)该函数的图象是中心对称图形;
(2)当x>0时,该函数在x=1时取得最小值2;
(3)在每个象限内,y的值随x值的增大而减小;
(4)y的值不可能为1.
7.已知函数y=x+,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是y与x的几组对应值:
x … 1 2 3 4 …
y … 4 3 2 m 2 3 4 …
请你根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究.
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律.
序号 函数图象的特征 函数变化规律
示例1 在直线x=1右侧,函数图象是呈上升状态 当x>1时,y随x的增大而增大
示例2 函数预想经过点 当x=2时,y=2
① 函数图象的最低点是(1,2)
② 在直线x=1左侧,函数图象呈下降状态
三.反比例函数图象的对称性
8.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
9.图中正比例函数和反比例函数的图象相交于A、B两点,分别以A、B两点为圆心,画与y轴相切的两个圆.若点A的坐标为(1,2),则图中两个阴影面积的和是 .
10.已知正比例函数y=k1x与反比例函数y=的一个交点是(2,3),则另一个交点是( , ).
四.反比例函数的性质
11.关于反比例函数y=﹣的图象性质,下列说法不正确的是( )
A.图象经过点(1,﹣2)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.图象关于原点对称
12.函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是 .
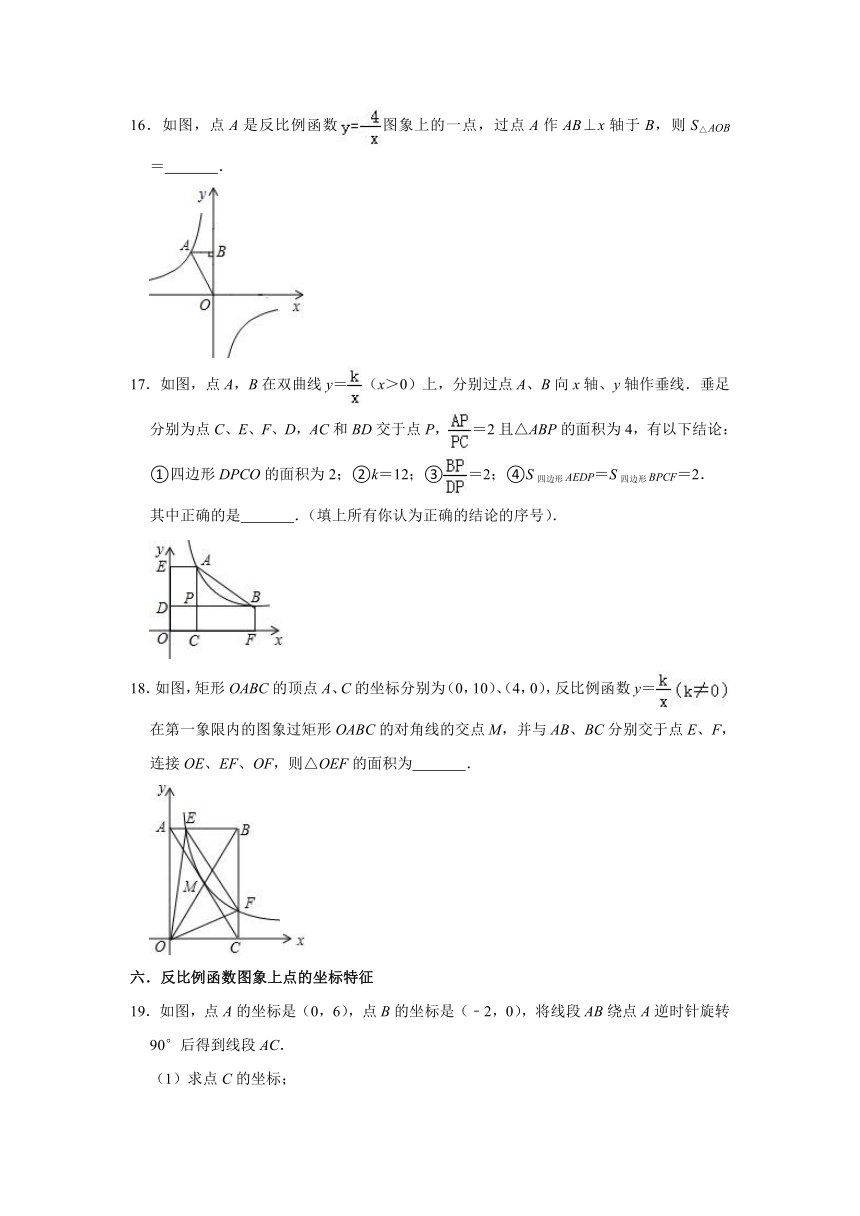
13.我们已经学习过反比例函数y=的图象和性质,请你回顾研究它的过程,运用所学知识对函数y=的图象和性质进行探索,并解决下列问题:
(1)该函数的图象大致是 .
(2)写出该函数两条不同类型的性质:
① ;
② .
14.若反比例函数y=的图象经过第二、四象限,则m的取值范围是 .
五.反比例函数系数k的几何意义
15.如图,双曲线y=(k>0,x>0)与正方形OABC的两边AB、BC分别相交于M,N两点,若A(6,0),△OMN的面积为10,动点P在x轴上,则PM+PN的最小值是( )
A.6 B.10 C.2 D.2
16.如图,点A是反比例函数图象上的一点,过点A作AB⊥x轴于B,则S△AOB= .
17.如图,点A,B在双曲线y=(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,=2且△ABP的面积为4,有以下结论:
①四边形DPCO的面积为2;②k=12;③=2;④S四边形AEDP=S四边形BPCF=2.
其中正确的是 .(填上所有你认为正确的结论的序号).
18.如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为 .
六.反比例函数图象上点的坐标特征
19.如图,点A的坐标是(0,6),点B的坐标是(﹣2,0),将线段AB绕点A逆时针旋转90°后得到线段AC.
(1)求点C的坐标;
(2)若反比例函数的图象恰好经过AC的中点D,求k的值.
七.待定系数法求反比例函数解析式
20.如图,平面直角坐标系中,菱形ABCD的边AD在x轴上,已知点 A(﹣1,0),点C(7,4),反比例函数经过点B,求反比例函数的解析式.
参考答案
一.反比例函数的定义
1.解:因为长方形的面积一定,所以长方形的宽x与长y成反比例函数关系.
2.解:观察图表可知,每对x,y的对应值的积是常数6,
因而xy=6,即y=,
故变量y与x之间的函数关系式:y=.
故答案为:y=
3.解:由函数是反比例函数,
k2﹣5=﹣1,且k﹣2≠0,
解得k=﹣2.
故答案为:﹣2.
二.反比例函数的图象
4.解:当k>0时,反比例函数的系数﹣k<0,反比例函数过二、四象限,一次函数过一、二、三象限,C图象符合;
当k<0时,反比例函数的系数﹣k>0,所以反比例函数过一、三象限,一次函数过二、三、四象限,没有符合图象.
故选:C.
5.解:∵反比例函数y1=的图象在第二象限,反比例函数y2=和y3=的图象在第一象限,
∴k1<0,k2>0,k3>0,
∵反比例函数y2=的图象在反比例函数y3=的图象的上方,
∴k2>k3,
∴k1<k3<k2.
故选:C.
6.解:(1)由图象可以看出函数图象上的每一个点都可以找到关于原点对称的点,故正确;
(2)结合图象的2个分支可以看出,在第一象限内,最低点的坐标为(1,2),故正确;
(3)在每个象限内,不同自变量的取值,函数值的变化是不同的,故错误;
(4)y的最小值为2,故不可能为1,故正确;
∴正确的有(1)(2)(4),
故答案为(1)(2)(4).
7.解:(1)x=1时,
m=y=1+1=2.
故答案为:2.
(2)如图
(3)由图像性质可推断:
①当x=1时,y=2;②当0<x<1时,y随x的增大而减小.
故答案为:①当x=1时,y=2;②当0<x<1时,y随x的增大而减小.
三.反比例函数图象的对称性
8.解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
9.解:若点A的坐标为(1,2),即圆的半径为1;
由反比例函数的对称性可得:两个阴影面积的和是S=π×12=π.
故答案为:π.
10.解:正比例函数y=k1x①与反比例函数②的一个交点是(2,3),
∴将(2,3)代入①得k1=,代入②得k2=6,即正比例函数y=x③,反比例函数y=④,
∴x=,解之得x=±2,把x=﹣2代入③得y=﹣3.
∴另一个交点是(﹣2,﹣3).
故答案为:﹣2;﹣3.
四.反比例函数的性质
11.A.当x=1时,代入反比例函数y=﹣得,y=﹣2,正确,故本选项不符合题意;
B.k=﹣2<0,图象位于第二、四象限,正确,故本选项不符合题意;
C.k=﹣2<0,在第二、四象限内y随x增大而增大,所以当x<0时,y随x的增大而增大,错误,故本选项符合题意;
D.反比例函数的图象可知,两个分支关于原点成中心对称,错误,故本选项不符合题意;
故选:C.
12.解:①由图象可以看出函数图象上的每一个点都可以找到关于原点对称的点,故正确;
②在每个象限内,不同自变量的取值,函数值的变化是不同的,故错误;
③y=x+=(﹣)2+4≥4,当且仅当x=2时取“=”.即在第一象限内,最低点的坐标为(2,4),故正确;
∴正确的有①③.
故答案为:①③.
13.解:(1)∵在函数y=中,|x|>0,
∴y>0,
当x>0时,y随着x的增大而减小;当x<0时,y随着x的增大而增大,
∴函数图象在第一、二象限;
故答案为:D;
(2)由图可得,该函数两条不同类型的性质为:
①图象关于y轴对称;②当x>0时,y随x增大而减小;当x<0时,y随x增大而增大.
故答案为:图象关于y轴对称;当x>0时,y随x增大而减小;当x<0时,y随x增大而增大.
14.解:∵反比例函数y=的图象经过第二、四象限,
∴m﹣2<0,
得:m<2.
故答案为:m<2.
五.反比例函数系数k的几何意义
15.解:∵A(6,0),
∴正方形OABC的边长为6.
∵OA=6,
∴M(6,).
∴AM=,BM=6﹣.
∵OC=6,
∴N(,6).
∴CN=,NB=6﹣.
∵△OMN的面积为10,
∴S正方形OABC﹣S△OCN﹣S△OAM﹣S△BMN=10.
∴.
解得:k=±24(负数不合题意,舍去).
∴k=24.
∴M(6,4),N(4,6).
∴BN=6﹣4=2,AM=4.
延长MA至M′,使AM′=AM,连接M′N交x轴于点P,如图,
则此时PM+PN最小,PM+PN=M′N.
在Rt△BM′N中,由勾股定理得:
M′N=.
即PM+PN的最小值为.
故选:C.
16.解:设A的坐标为(a,b)(a<0,b>0),
∴OB=b,AB=﹣a,
又A在反比例函数y=﹣图象上,
将x=a,y=b代入反比例函数解析式得:b=﹣,即﹣ab=4,
又△AOB为直角三角形,
则S△AOB=OB AB=﹣ab=2.
故答案为:2
17.解:设点A坐标为(m,),点B坐标为(n,)(0<m<n).
由已知得:,
解得:.
故②k=12,不成立;
①四边形DPCO的面积S=OC PC=m =m =2,
即①成立;
③BP=n﹣m=2m,DP=m,
故=2,③成立;
④S四边形AEDP=AP DP=(﹣) m=4,
S四边形BPCF=BP PC=(n﹣m) =4,
故S四边形AEDP=S四边形BPCF=4,④不成立.
故答案为:①③.
18.解:∵矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),
∴B(4,10),
∵M是矩形OABC对角线的交点,
∴OM=MB,
∴M点的坐标是(2,5),
把x=2,y=5代入y=,得k=10,
∴反比例函数的解析式为y=,
当y=10时,x=1,∴E(1,10);
当x=4时,y=,∴F(4,).
△OEF的面积=S矩形OABC﹣S△OAE﹣S△BEF
=10×4﹣×10×1﹣×4×﹣×3×
=40﹣5﹣5﹣
=.
故答案为.
六.反比例函数图象上点的坐标特征
19.解:(1)作CM⊥y轴于M.
∵∠AOB=∠CMA=∠BAC=90°,
∴∠BAO+∠CAM=90°,∠ABO+∠BAO=90°,
∴∠ABO=∠CAM,
∵BA=AC,
∴△AOB≌△CMA(AAS),
∴OB=AM,OA=CM,
∵点A的坐标是(0,6),点B的坐标是(﹣2,0),
∴OA=6,OB=2,
∴CM=6,AM=2,
∴OM=4,
∴点C的坐标是(6,4);
(2)∵点A的坐标是(0,6),点C的坐标是(6,4);
∴D(3,5),
∵反比例函数的图象经过点D,
∴,解得k=15,
故k的值是15.
七.待定系数法求反比例函数解析式
20.解:设菱形的边长为a,作BM⊥x轴于M,
∵点 A(﹣1,0),点C(7,4),
∴B(7﹣a,4),
∴AM=7﹣a+1=8+a,BM=4,
在Rt△ABM中,AB2=AM2+BM2,
∴a2=(8﹣a)2+42,解得a=5,
∴B(2,4),
∵反比例函数经过点B,
∴k=2×4=8,
∴反比例函数的解析式为y=.
一.反比例函数的定义
1.如图用方砖铺地时,若地面很大,而方砖的数量有限,当铺成的地面为长方形时,长方形的宽x与长y成 关系.
2.已知变量y与变量x之间的对应值如下表:
x … 1 2 3 4 5 6 …
y … 6 3 2 1.5 1.2 1 …
试求出变量y与x之间的函数关系式: .
3.已知函数,当k= 时,y是x的反比例函数.
二.反比例函数的图象
4.已知关于x的函数y=k(x+1)和,它们在同一坐标系中的图象大致是( )
A. B.
C. D.
5.如图是三个反比例函数的图象的分支,其中k1,k2,k3的大小关系是( )
A.k1>k2>k3 B.k1<k2<k3 C.k2>k3>k1 D.k1=k2>k3
6.函数的图象如图所示,下列对该函数性质的论断正确的是
(1)该函数的图象是中心对称图形;
(2)当x>0时,该函数在x=1时取得最小值2;
(3)在每个象限内,y的值随x值的增大而减小;
(4)y的值不可能为1.
7.已知函数y=x+,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是y与x的几组对应值:
x … 1 2 3 4 …
y … 4 3 2 m 2 3 4 …
请你根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究.
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律.
序号 函数图象的特征 函数变化规律
示例1 在直线x=1右侧,函数图象是呈上升状态 当x>1时,y随x的增大而增大
示例2 函数预想经过点 当x=2时,y=2
① 函数图象的最低点是(1,2)
② 在直线x=1左侧,函数图象呈下降状态
三.反比例函数图象的对称性
8.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
9.图中正比例函数和反比例函数的图象相交于A、B两点,分别以A、B两点为圆心,画与y轴相切的两个圆.若点A的坐标为(1,2),则图中两个阴影面积的和是 .
10.已知正比例函数y=k1x与反比例函数y=的一个交点是(2,3),则另一个交点是( , ).
四.反比例函数的性质
11.关于反比例函数y=﹣的图象性质,下列说法不正确的是( )
A.图象经过点(1,﹣2)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.图象关于原点对称
12.函数y1=x与y2=的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是 .
13.我们已经学习过反比例函数y=的图象和性质,请你回顾研究它的过程,运用所学知识对函数y=的图象和性质进行探索,并解决下列问题:
(1)该函数的图象大致是 .
(2)写出该函数两条不同类型的性质:
① ;
② .
14.若反比例函数y=的图象经过第二、四象限,则m的取值范围是 .
五.反比例函数系数k的几何意义
15.如图,双曲线y=(k>0,x>0)与正方形OABC的两边AB、BC分别相交于M,N两点,若A(6,0),△OMN的面积为10,动点P在x轴上,则PM+PN的最小值是( )
A.6 B.10 C.2 D.2
16.如图,点A是反比例函数图象上的一点,过点A作AB⊥x轴于B,则S△AOB= .
17.如图,点A,B在双曲线y=(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,=2且△ABP的面积为4,有以下结论:
①四边形DPCO的面积为2;②k=12;③=2;④S四边形AEDP=S四边形BPCF=2.
其中正确的是 .(填上所有你认为正确的结论的序号).
18.如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为 .
六.反比例函数图象上点的坐标特征
19.如图,点A的坐标是(0,6),点B的坐标是(﹣2,0),将线段AB绕点A逆时针旋转90°后得到线段AC.
(1)求点C的坐标;
(2)若反比例函数的图象恰好经过AC的中点D,求k的值.
七.待定系数法求反比例函数解析式
20.如图,平面直角坐标系中,菱形ABCD的边AD在x轴上,已知点 A(﹣1,0),点C(7,4),反比例函数经过点B,求反比例函数的解析式.
参考答案
一.反比例函数的定义
1.解:因为长方形的面积一定,所以长方形的宽x与长y成反比例函数关系.
2.解:观察图表可知,每对x,y的对应值的积是常数6,
因而xy=6,即y=,
故变量y与x之间的函数关系式:y=.
故答案为:y=
3.解:由函数是反比例函数,
k2﹣5=﹣1,且k﹣2≠0,
解得k=﹣2.
故答案为:﹣2.
二.反比例函数的图象
4.解:当k>0时,反比例函数的系数﹣k<0,反比例函数过二、四象限,一次函数过一、二、三象限,C图象符合;
当k<0时,反比例函数的系数﹣k>0,所以反比例函数过一、三象限,一次函数过二、三、四象限,没有符合图象.
故选:C.
5.解:∵反比例函数y1=的图象在第二象限,反比例函数y2=和y3=的图象在第一象限,
∴k1<0,k2>0,k3>0,
∵反比例函数y2=的图象在反比例函数y3=的图象的上方,
∴k2>k3,
∴k1<k3<k2.
故选:C.
6.解:(1)由图象可以看出函数图象上的每一个点都可以找到关于原点对称的点,故正确;
(2)结合图象的2个分支可以看出,在第一象限内,最低点的坐标为(1,2),故正确;
(3)在每个象限内,不同自变量的取值,函数值的变化是不同的,故错误;
(4)y的最小值为2,故不可能为1,故正确;
∴正确的有(1)(2)(4),
故答案为(1)(2)(4).
7.解:(1)x=1时,
m=y=1+1=2.
故答案为:2.
(2)如图
(3)由图像性质可推断:
①当x=1时,y=2;②当0<x<1时,y随x的增大而减小.
故答案为:①当x=1时,y=2;②当0<x<1时,y随x的增大而减小.
三.反比例函数图象的对称性
8.解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
9.解:若点A的坐标为(1,2),即圆的半径为1;
由反比例函数的对称性可得:两个阴影面积的和是S=π×12=π.
故答案为:π.
10.解:正比例函数y=k1x①与反比例函数②的一个交点是(2,3),
∴将(2,3)代入①得k1=,代入②得k2=6,即正比例函数y=x③,反比例函数y=④,
∴x=,解之得x=±2,把x=﹣2代入③得y=﹣3.
∴另一个交点是(﹣2,﹣3).
故答案为:﹣2;﹣3.
四.反比例函数的性质
11.A.当x=1时,代入反比例函数y=﹣得,y=﹣2,正确,故本选项不符合题意;
B.k=﹣2<0,图象位于第二、四象限,正确,故本选项不符合题意;
C.k=﹣2<0,在第二、四象限内y随x增大而增大,所以当x<0时,y随x的增大而增大,错误,故本选项符合题意;
D.反比例函数的图象可知,两个分支关于原点成中心对称,错误,故本选项不符合题意;
故选:C.
12.解:①由图象可以看出函数图象上的每一个点都可以找到关于原点对称的点,故正确;
②在每个象限内,不同自变量的取值,函数值的变化是不同的,故错误;
③y=x+=(﹣)2+4≥4,当且仅当x=2时取“=”.即在第一象限内,最低点的坐标为(2,4),故正确;
∴正确的有①③.
故答案为:①③.
13.解:(1)∵在函数y=中,|x|>0,
∴y>0,
当x>0时,y随着x的增大而减小;当x<0时,y随着x的增大而增大,
∴函数图象在第一、二象限;
故答案为:D;
(2)由图可得,该函数两条不同类型的性质为:
①图象关于y轴对称;②当x>0时,y随x增大而减小;当x<0时,y随x增大而增大.
故答案为:图象关于y轴对称;当x>0时,y随x增大而减小;当x<0时,y随x增大而增大.
14.解:∵反比例函数y=的图象经过第二、四象限,
∴m﹣2<0,
得:m<2.
故答案为:m<2.
五.反比例函数系数k的几何意义
15.解:∵A(6,0),
∴正方形OABC的边长为6.
∵OA=6,
∴M(6,).
∴AM=,BM=6﹣.
∵OC=6,
∴N(,6).
∴CN=,NB=6﹣.
∵△OMN的面积为10,
∴S正方形OABC﹣S△OCN﹣S△OAM﹣S△BMN=10.
∴.
解得:k=±24(负数不合题意,舍去).
∴k=24.
∴M(6,4),N(4,6).
∴BN=6﹣4=2,AM=4.
延长MA至M′,使AM′=AM,连接M′N交x轴于点P,如图,
则此时PM+PN最小,PM+PN=M′N.
在Rt△BM′N中,由勾股定理得:
M′N=.
即PM+PN的最小值为.
故选:C.
16.解:设A的坐标为(a,b)(a<0,b>0),
∴OB=b,AB=﹣a,
又A在反比例函数y=﹣图象上,
将x=a,y=b代入反比例函数解析式得:b=﹣,即﹣ab=4,
又△AOB为直角三角形,
则S△AOB=OB AB=﹣ab=2.
故答案为:2
17.解:设点A坐标为(m,),点B坐标为(n,)(0<m<n).
由已知得:,
解得:.
故②k=12,不成立;
①四边形DPCO的面积S=OC PC=m =m =2,
即①成立;
③BP=n﹣m=2m,DP=m,
故=2,③成立;
④S四边形AEDP=AP DP=(﹣) m=4,
S四边形BPCF=BP PC=(n﹣m) =4,
故S四边形AEDP=S四边形BPCF=4,④不成立.
故答案为:①③.
18.解:∵矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),
∴B(4,10),
∵M是矩形OABC对角线的交点,
∴OM=MB,
∴M点的坐标是(2,5),
把x=2,y=5代入y=,得k=10,
∴反比例函数的解析式为y=,
当y=10时,x=1,∴E(1,10);
当x=4时,y=,∴F(4,).
△OEF的面积=S矩形OABC﹣S△OAE﹣S△BEF
=10×4﹣×10×1﹣×4×﹣×3×
=40﹣5﹣5﹣
=.
故答案为.
六.反比例函数图象上点的坐标特征
19.解:(1)作CM⊥y轴于M.
∵∠AOB=∠CMA=∠BAC=90°,
∴∠BAO+∠CAM=90°,∠ABO+∠BAO=90°,
∴∠ABO=∠CAM,
∵BA=AC,
∴△AOB≌△CMA(AAS),
∴OB=AM,OA=CM,
∵点A的坐标是(0,6),点B的坐标是(﹣2,0),
∴OA=6,OB=2,
∴CM=6,AM=2,
∴OM=4,
∴点C的坐标是(6,4);
(2)∵点A的坐标是(0,6),点C的坐标是(6,4);
∴D(3,5),
∵反比例函数的图象经过点D,
∴,解得k=15,
故k的值是15.
七.待定系数法求反比例函数解析式
20.解:设菱形的边长为a,作BM⊥x轴于M,
∵点 A(﹣1,0),点C(7,4),
∴B(7﹣a,4),
∴AM=7﹣a+1=8+a,BM=4,
在Rt△ABM中,AB2=AM2+BM2,
∴a2=(8﹣a)2+42,解得a=5,
∴B(2,4),
∵反比例函数经过点B,
∴k=2×4=8,
∴反比例函数的解析式为y=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
