北师大版七年级数学上册第一章丰富的图形世界期中复习训练(附答案)
文档属性
| 名称 | 北师大版七年级数学上册第一章丰富的图形世界期中复习训练(附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 241.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 21:09:50 | ||
图片预览

文档简介
2022-2023学年北师大版七年级数学上册《第1章丰富的图形世界》期中复习训练(附答案)
一.选择题
1.如果一个物体有七个顶点七个面,那么这个物体一定是( )
A.五棱锥 B.五棱柱 C.六棱锥 D.七棱锥
2.若一个棱柱有12个顶点,则下列说法正确的是( )
A.这个棱柱是十二棱柱
B.这个棱柱有4个侧面
C.这个棱柱的底面是八边形
D.这个棱柱有6条侧棱
3.如图几何体面的个数为( )
A.1 B.2 C.3 D.4
4.将一个等腰三角形绕它的底边旋转一周得到的几何体为( )
A. B. C. D.
5.求圆柱形水桶能装多少升水,是求它的 ;制作一节圆柱形通风管要多少铁皮,是求它的 .( )
A.容积、侧面积 B.容积、表面积
C.体积、表面积
6.如图是某一正方体的平面展开图,则该正方体是( )
A. B. C. D.
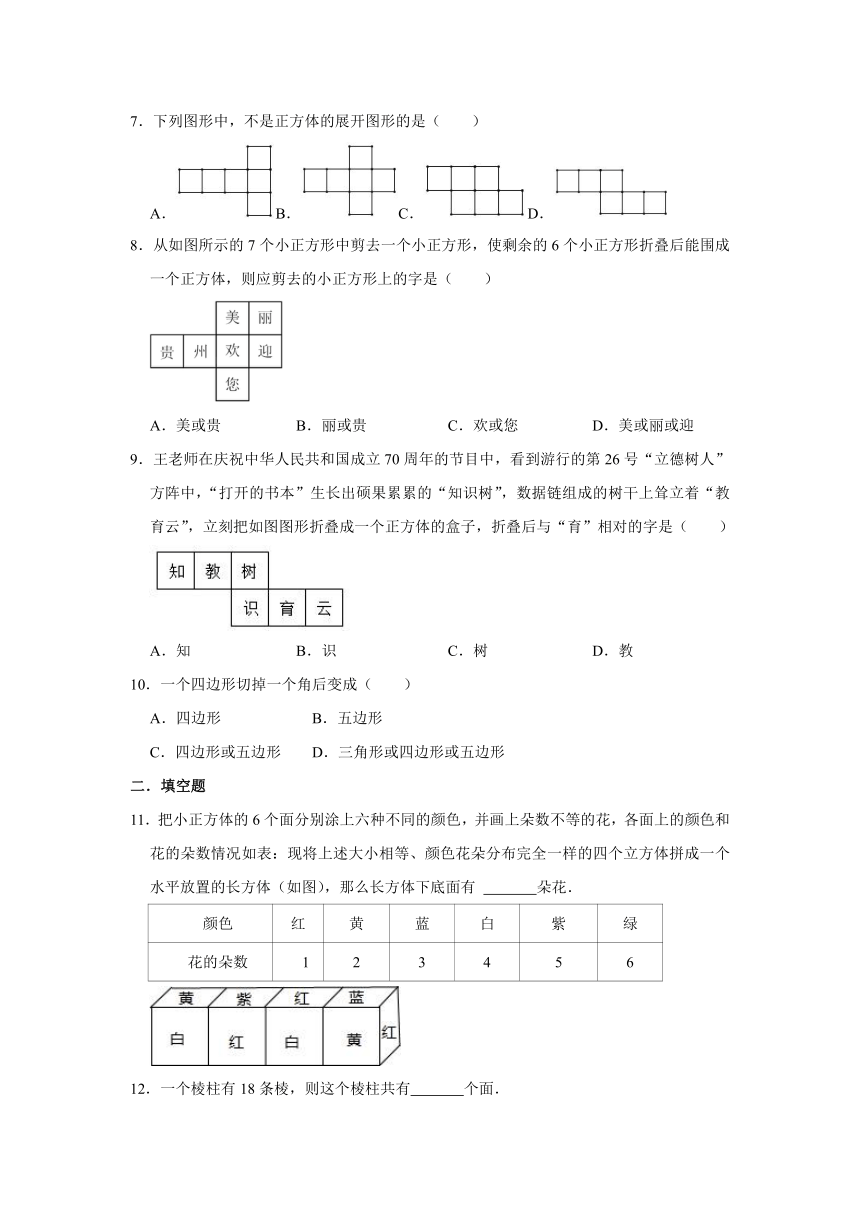
7.下列图形中,不是正方体的展开图形的是( )
A.B.C.D.
8.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去的小正方形上的字是( )
A.美或贵 B.丽或贵 C.欢或您 D.美或丽或迎
9.王老师在庆祝中华人民共和国成立70周年的节目中,看到游行的第26号“立德树人”方阵中,“打开的书本”生长出硕果累累的“知识树”,数据链组成的树干上耸立着“教育云”,立刻把如图图形折叠成一个正方体的盒子,折叠后与“育”相对的字是( )
A.知 B.识 C.树 D.教
10.一个四边形切掉一个角后变成( )
A.四边形 B.五边形
C.四边形或五边形 D.三角形或四边形或五边形
二.填空题
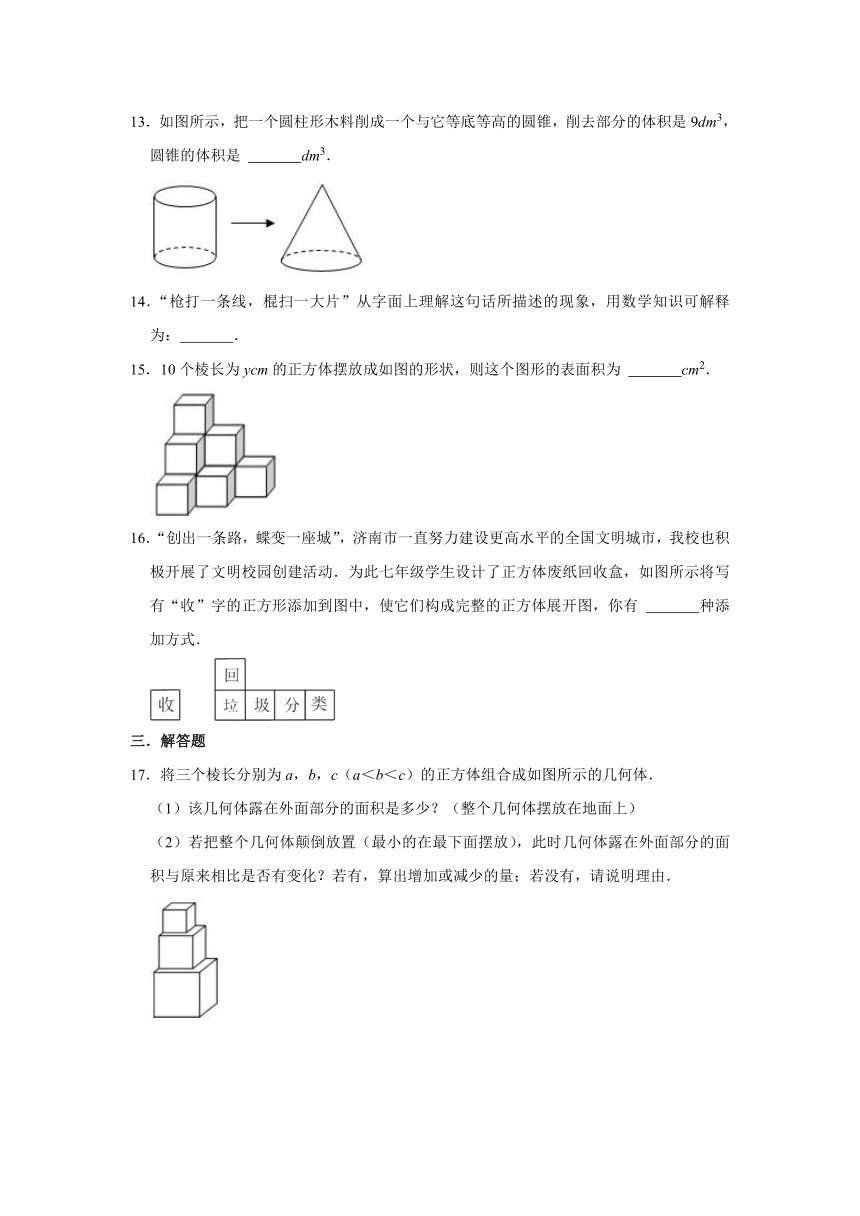
11.把小正方体的6个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色和花的朵数情况如表:现将上述大小相等、颜色花朵分布完全一样的四个立方体拼成一个水平放置的长方体(如图),那么长方体下底面有 朵花.
颜色 红 黄 蓝 白 紫 绿
花的朵数 1 2 3 4 5 6
12.一个棱柱有18条棱,则这个棱柱共有 个面.
13.如图所示,把一个圆柱形木料削成一个与它等底等高的圆锥,削去部分的体积是9dm3,圆锥的体积是 dm3.
14.“枪打一条线,棍扫一大片”从字面上理解这句话所描述的现象,用数学知识可解释为: .
15.10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2.
16.“创出一条路,蝶变一座城”,济南市一直努力建设更高水平的全国文明城市,我校也积极开展了文明校园创建活动.为此七年级学生设计了正方体废纸回收盒,如图所示将写有“收”字的正方形添加到图中,使它们构成完整的正方体展开图,你有 种添加方式.
三.解答题
17.将三个棱长分别为a,b,c(a<b<c)的正方体组合成如图所示的几何体.
(1)该几何体露在外面部分的面积是多少?(整个几何体摆放在地面上)
(2)若把整个几何体颠倒放置(最小的在最下面摆放),此时几何体露在外面部分的面积与原来相比是否有变化?若有,算出增加或减少的量;若没有,请说明理由.
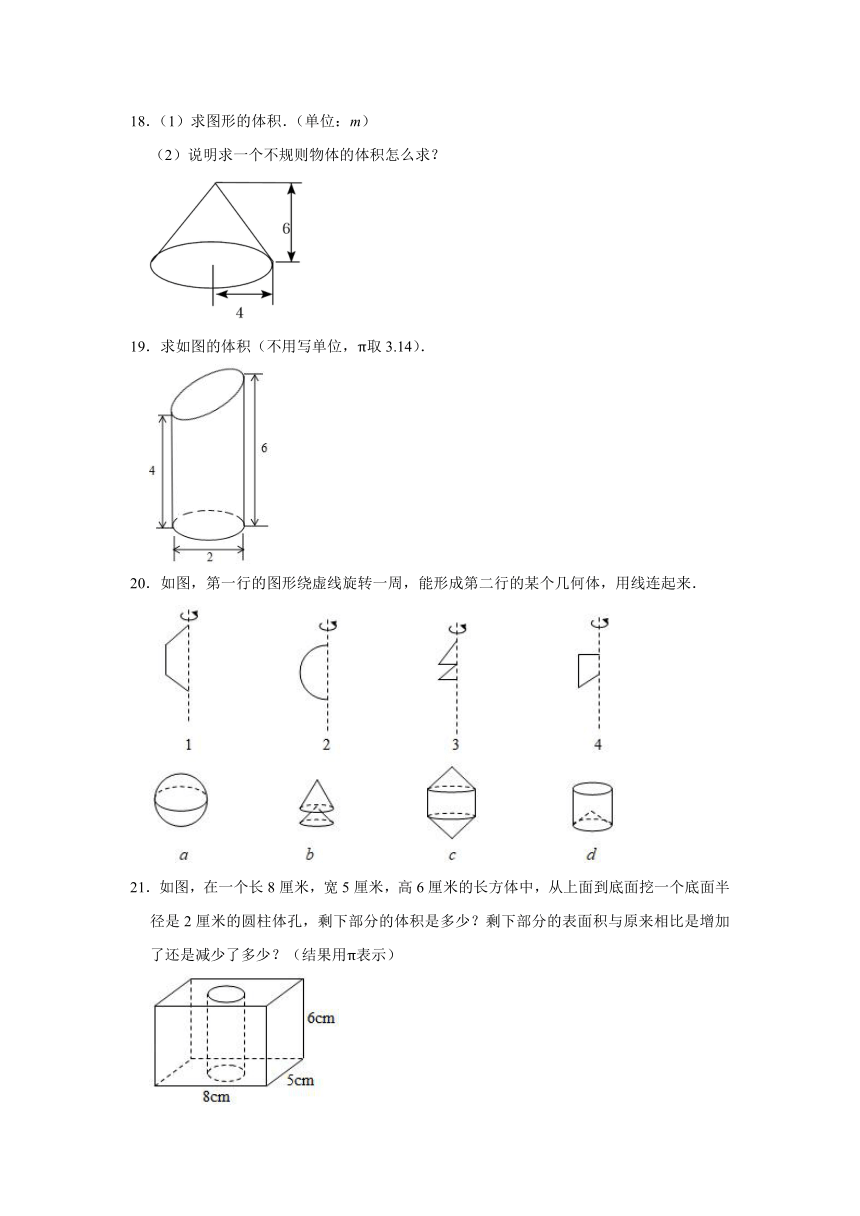
18.(1)求图形的体积.(单位:m)
(2)说明求一个不规则物体的体积怎么求?
19.求如图的体积(不用写单位,π取3.14).
20.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
21.如图,在一个长8厘米,宽5厘米,高6厘米的长方体中,从上面到底面挖一个底面半径是2厘米的圆柱体孔,剩下部分的体积是多少?剩下部分的表面积与原来相比是增加了还是减少了多少?(结果用π表示)
22.有一种牛奶软包装盒如图1所示,为了生产这种包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有 .
(2)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和).
23.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是 ,其底面半径为 .
(2)根据图中所给信息,求该几何体的侧面积和体积.(结果保留π)
参考答案
一.选择题
1.解:如果一个物体有七个顶点七个面,那么这个物体一定是六棱锥.
故选:C.
2.解:∵棱柱有12 个顶点,
∴上下底面各有6个顶点,即这个棱柱是六棱柱,有6个侧面,底面是六边形,有6条侧棱.
故选:D.
3.解:面有平面和曲面两种.例如包围着长方体的面是平面,包围球的面是曲面,且是一个面.
故选:A.
4.解:将一个等腰三角形绕它的底边旋转一周得到的几何体是两个具有同底面的圆锥组合体,
因此选项B中的几何体符合题意,
故选:B.
5.解:根据题意可得:求圆柱形水桶能装多少升水,是求它的容积;
因为圆柱形通风管只有侧面,没有底面,所以制作一节圆柱形通风管要多少铁皮就是求它的侧面积.
故选:A.
6.解:由正方体的展开图可知,两个圆是相对的面,故选项A、B不合题意;
没有阴影的圆与直角三角形的直角相邻,故选项C不合题意;
选项D符合该正方体的平面展开图,
故选:D.
7.解:正方体共有11种表面展开图,
A、B、D能围成正方体;
C不能,折叠后有两个面重合,不能折成正方体.
故选:C.
8.解:由图可得,与“您”相对的面不唯一,与“州”相对的面不唯一,
从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,应剪去的小正方形上的字是美或丽或迎.
故选:D.
9.解:由正方体展开图对面的对应特点,教与育是对面.
故选:D.
10.解:如图可知,一个四边形截去一个角后变成三角形或四边形或五边形.
故选:D.
二.填空题
11.解:由题意可得,右二的立方体的下侧为绿色,右三的为黄色,左一的为紫色,
那么长方体的下底面共有花数4+6+2+5=17朵.
故答案为:17.
12.解:由n棱柱有3n条棱,
所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,
而六棱柱有6+2=8个面,
故答案为:八.
13.解:∵圆柱的体积=底面积×高,圆锥的体积=底面积×高,
∴削去部分的体积=圆锥的体积的2倍,
∴9÷2=4.5(立方分米),
∴圆锥的体积是4.5dm3,
故答案为:4.5.
14.解:“枪打一条线,棍扫一大片”从字面上理解这句话所描述的现象,用数学知识可解释为:点动成线,线动成面,
故答案为:点动成线,线动成面.
15.解:因为这个几何体的主视图,左视图,俯视图都各有6个面,
所以:则这个图形的表面积为:6×6 y2=36y2(平方厘米),
故答案为:36y2.
16.解:“收”字分别放在“垃”、“圾”、“分”、“类”下方均可成完整的正方体展开图,
所以有4种添加方式.
故答案为:4.
三.解答题
17.解:(1)几何体露在外面部分的面积是4a2+4b2+5c2;
(2)与原来相比增加了,
由[4a2+4b2+5c2+(c2﹣a2)]﹣(4a2+4b2+5c2)=c2﹣a2,
∵a<c,
∴c2﹣a2>0,
∴增加了c2﹣a2.
18.解:(1)由题意得:
×π×42×6
=×π×16×6
=32π(立方米)
答:它的体积是32π立方米;
(2)只要把不规则的物体放在装有水的规则容器里,水就会上升,水上升后比原来多出来的体积,就是不规则物体的体积.
19.解:由题意得:
π×()2×4+×π×()2×(6﹣4)
=4π+π
=5π,
答:上图的体积为:5π.
20.解:连线如图:
21.解:V=8×5×6﹣π×22×6=240﹣24π(立方厘米).
2π×2×6﹣2π×22=16π(平方厘米)
表面积增加了16π平方厘米.
22.解:(1)给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有甲、丙;
故答案为:甲、丙;
(2)S侧=(b+a+b+a)h=2ah+2bh;
S表=S侧+2S底=2ah+2bh+2ab.
23.解:(1)该几何体的名称是圆柱,其底面半径为1,
故答案为:圆柱;1;
(2)该几何体的侧面积为:2π×1×3=6π;
该几何体的体积=π×12×3=3π.
一.选择题
1.如果一个物体有七个顶点七个面,那么这个物体一定是( )
A.五棱锥 B.五棱柱 C.六棱锥 D.七棱锥
2.若一个棱柱有12个顶点,则下列说法正确的是( )
A.这个棱柱是十二棱柱
B.这个棱柱有4个侧面
C.这个棱柱的底面是八边形
D.这个棱柱有6条侧棱
3.如图几何体面的个数为( )
A.1 B.2 C.3 D.4
4.将一个等腰三角形绕它的底边旋转一周得到的几何体为( )
A. B. C. D.
5.求圆柱形水桶能装多少升水,是求它的 ;制作一节圆柱形通风管要多少铁皮,是求它的 .( )
A.容积、侧面积 B.容积、表面积
C.体积、表面积
6.如图是某一正方体的平面展开图,则该正方体是( )
A. B. C. D.
7.下列图形中,不是正方体的展开图形的是( )
A.B.C.D.
8.从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,则应剪去的小正方形上的字是( )
A.美或贵 B.丽或贵 C.欢或您 D.美或丽或迎
9.王老师在庆祝中华人民共和国成立70周年的节目中,看到游行的第26号“立德树人”方阵中,“打开的书本”生长出硕果累累的“知识树”,数据链组成的树干上耸立着“教育云”,立刻把如图图形折叠成一个正方体的盒子,折叠后与“育”相对的字是( )
A.知 B.识 C.树 D.教
10.一个四边形切掉一个角后变成( )
A.四边形 B.五边形
C.四边形或五边形 D.三角形或四边形或五边形
二.填空题
11.把小正方体的6个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色和花的朵数情况如表:现将上述大小相等、颜色花朵分布完全一样的四个立方体拼成一个水平放置的长方体(如图),那么长方体下底面有 朵花.
颜色 红 黄 蓝 白 紫 绿
花的朵数 1 2 3 4 5 6
12.一个棱柱有18条棱,则这个棱柱共有 个面.
13.如图所示,把一个圆柱形木料削成一个与它等底等高的圆锥,削去部分的体积是9dm3,圆锥的体积是 dm3.
14.“枪打一条线,棍扫一大片”从字面上理解这句话所描述的现象,用数学知识可解释为: .
15.10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2.
16.“创出一条路,蝶变一座城”,济南市一直努力建设更高水平的全国文明城市,我校也积极开展了文明校园创建活动.为此七年级学生设计了正方体废纸回收盒,如图所示将写有“收”字的正方形添加到图中,使它们构成完整的正方体展开图,你有 种添加方式.
三.解答题
17.将三个棱长分别为a,b,c(a<b<c)的正方体组合成如图所示的几何体.
(1)该几何体露在外面部分的面积是多少?(整个几何体摆放在地面上)
(2)若把整个几何体颠倒放置(最小的在最下面摆放),此时几何体露在外面部分的面积与原来相比是否有变化?若有,算出增加或减少的量;若没有,请说明理由.
18.(1)求图形的体积.(单位:m)
(2)说明求一个不规则物体的体积怎么求?
19.求如图的体积(不用写单位,π取3.14).
20.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
21.如图,在一个长8厘米,宽5厘米,高6厘米的长方体中,从上面到底面挖一个底面半径是2厘米的圆柱体孔,剩下部分的体积是多少?剩下部分的表面积与原来相比是增加了还是减少了多少?(结果用π表示)
22.有一种牛奶软包装盒如图1所示,为了生产这种包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有 .
(2)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和).
23.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是 ,其底面半径为 .
(2)根据图中所给信息,求该几何体的侧面积和体积.(结果保留π)
参考答案
一.选择题
1.解:如果一个物体有七个顶点七个面,那么这个物体一定是六棱锥.
故选:C.
2.解:∵棱柱有12 个顶点,
∴上下底面各有6个顶点,即这个棱柱是六棱柱,有6个侧面,底面是六边形,有6条侧棱.
故选:D.
3.解:面有平面和曲面两种.例如包围着长方体的面是平面,包围球的面是曲面,且是一个面.
故选:A.
4.解:将一个等腰三角形绕它的底边旋转一周得到的几何体是两个具有同底面的圆锥组合体,
因此选项B中的几何体符合题意,
故选:B.
5.解:根据题意可得:求圆柱形水桶能装多少升水,是求它的容积;
因为圆柱形通风管只有侧面,没有底面,所以制作一节圆柱形通风管要多少铁皮就是求它的侧面积.
故选:A.
6.解:由正方体的展开图可知,两个圆是相对的面,故选项A、B不合题意;
没有阴影的圆与直角三角形的直角相邻,故选项C不合题意;
选项D符合该正方体的平面展开图,
故选:D.
7.解:正方体共有11种表面展开图,
A、B、D能围成正方体;
C不能,折叠后有两个面重合,不能折成正方体.
故选:C.
8.解:由图可得,与“您”相对的面不唯一,与“州”相对的面不唯一,
从如图所示的7个小正方形中剪去一个小正方形,使剩余的6个小正方形折叠后能围成一个正方体,应剪去的小正方形上的字是美或丽或迎.
故选:D.
9.解:由正方体展开图对面的对应特点,教与育是对面.
故选:D.
10.解:如图可知,一个四边形截去一个角后变成三角形或四边形或五边形.
故选:D.
二.填空题
11.解:由题意可得,右二的立方体的下侧为绿色,右三的为黄色,左一的为紫色,
那么长方体的下底面共有花数4+6+2+5=17朵.
故答案为:17.
12.解:由n棱柱有3n条棱,
所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,
而六棱柱有6+2=8个面,
故答案为:八.
13.解:∵圆柱的体积=底面积×高,圆锥的体积=底面积×高,
∴削去部分的体积=圆锥的体积的2倍,
∴9÷2=4.5(立方分米),
∴圆锥的体积是4.5dm3,
故答案为:4.5.
14.解:“枪打一条线,棍扫一大片”从字面上理解这句话所描述的现象,用数学知识可解释为:点动成线,线动成面,
故答案为:点动成线,线动成面.
15.解:因为这个几何体的主视图,左视图,俯视图都各有6个面,
所以:则这个图形的表面积为:6×6 y2=36y2(平方厘米),
故答案为:36y2.
16.解:“收”字分别放在“垃”、“圾”、“分”、“类”下方均可成完整的正方体展开图,
所以有4种添加方式.
故答案为:4.
三.解答题
17.解:(1)几何体露在外面部分的面积是4a2+4b2+5c2;
(2)与原来相比增加了,
由[4a2+4b2+5c2+(c2﹣a2)]﹣(4a2+4b2+5c2)=c2﹣a2,
∵a<c,
∴c2﹣a2>0,
∴增加了c2﹣a2.
18.解:(1)由题意得:
×π×42×6
=×π×16×6
=32π(立方米)
答:它的体积是32π立方米;
(2)只要把不规则的物体放在装有水的规则容器里,水就会上升,水上升后比原来多出来的体积,就是不规则物体的体积.
19.解:由题意得:
π×()2×4+×π×()2×(6﹣4)
=4π+π
=5π,
答:上图的体积为:5π.
20.解:连线如图:
21.解:V=8×5×6﹣π×22×6=240﹣24π(立方厘米).
2π×2×6﹣2π×22=16π(平方厘米)
表面积增加了16π平方厘米.
22.解:(1)给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有甲、丙;
故答案为:甲、丙;
(2)S侧=(b+a+b+a)h=2ah+2bh;
S表=S侧+2S底=2ah+2bh+2ab.
23.解:(1)该几何体的名称是圆柱,其底面半径为1,
故答案为:圆柱;1;
(2)该几何体的侧面积为:2π×1×3=6π;
该几何体的体积=π×12×3=3π.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
